Advances in Applied Mathematics
Vol.07 No.04(2018), Article ID:24704,5
pages
10.12677/AAM.2018.74052
The Upper Bound of the Interval Edge-Coloring of the Generalized θ-Chain
Xun Chen
College of Mathematics and System Science, Xinjiang University, Urumqi Xinjiang
Received: Apr. 11th, 2018; accepted: Apr. 21st, 2018; published: Apr. 28th, 2018

ABSTRACT
An edge-coloring of a graph G with colors  is an interval t-coloring if all colors are used, and the colors of edges incident to each vertex of G are distinct and form an interval of integer. A graph G is interval colorable if it has an interval t-coloring for some positive integer t. The set of all interval colorable graphs is denoted by
is an interval t-coloring if all colors are used, and the colors of edges incident to each vertex of G are distinct and form an interval of integer. A graph G is interval colorable if it has an interval t-coloring for some positive integer t. The set of all interval colorable graphs is denoted by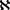 . For any
. For any , G has a interval t-coloring. w(G) and W(G) are the minimum and maximum numbers of t. A generalized θ-chain, denoted by
, G has a interval t-coloring. w(G) and W(G) are the minimum and maximum numbers of t. A generalized θ-chain, denoted by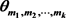 , is a simple graph obtained by substituting
, is a simple graph obtained by substituting 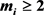 pairwise internally disjoint
pairwise internally disjoint 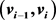 -paths for each edge
-paths for each edge  of the path
of the path , where
, where . In this paper, we give a tight upper bound on
. In this paper, we give a tight upper bound on .
.
Keywords:Interval Edge-Coloring, Upper Bound, Generalized θ-Graph, Generalized θ-Chain

广义θ-链的区间边着色的上界
陈勋
新疆大学数学与系统科学学院,新疆 乌鲁木齐
收稿日期:2018年4月11日;录用日期:2018年4月21日;发布日期:2018年4月28日

摘 要
图G的一个用了颜色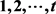 的边着色称为区间t-着色,如果所有t种颜色都被用到,并且关联于G的同一个顶点的边上颜色各不相同且这些颜色构成了一个连续的整数区间。G称作是可区间着色的,如果对某个正整数t,G有一个区间t-着色。所有可区间着色的图构成的集合记作
的边着色称为区间t-着色,如果所有t种颜色都被用到,并且关联于G的同一个顶点的边上颜色各不相同且这些颜色构成了一个连续的整数区间。G称作是可区间着色的,如果对某个正整数t,G有一个区间t-着色。所有可区间着色的图构成的集合记作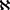 。对图
。对图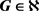 ,使得G有一个区间t-着色的t的最小值和最大值分别记作
,使得G有一个区间t-着色的t的最小值和最大值分别记作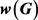 和
和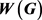 。广义θ-链,记作
。广义θ-链,记作 ,是把路
,是把路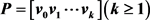 的每一条边
的每一条边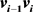 用
用 条两两内部不交的
条两两内部不交的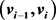 -路替换掉而得到的简单图,这里
-路替换掉而得到的简单图,这里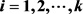 。在本文中,我们给出了
。在本文中,我们给出了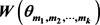 的一个紧的上界。
的一个紧的上界。
关键词 :区间边着色,上界,广义θ-图,广义θ-链

Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
 和
和 分别表示图G的顶点集和边集,
分别表示图G的顶点集和边集,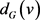 表示顶点
表示顶点 在图G中的度,
在图G中的度,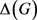 表示图G的最大度,
表示图G的最大度,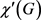 表示图G的边色数,
表示图G的边色数,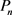 表示n个顶点的路。
表示n个顶点的路。
如果α是图G的一个正常边着色,那么与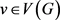 关联的边上的颜色构成的集合,记作
关联的边上的颜色构成的集合,记作 。我们用
。我们用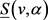 和
和 分别表示
分别表示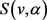 的最小色值和最大色值。
的最小色值和最大色值。
图G的一个用了颜色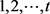 的正常边着色α称为区间t-着色,如果所有t种颜色都被用到,并且对任意的
的正常边着色α称为区间t-着色,如果所有t种颜色都被用到,并且对任意的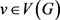 ,
,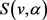 是连续的。图G称为是可区间着色的,如果对某个正整数t,G有一个区间t-着色。所有可区间着色的图构成的集合记作
是连续的。图G称为是可区间着色的,如果对某个正整数t,G有一个区间t-着色。所有可区间着色的图构成的集合记作 。对图
。对图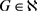 ,使得G有一个区间t-着色的t的最小值和最大值分别记作w(G)和W(G)。
,使得G有一个区间t-着色的t的最小值和最大值分别记作w(G)和W(G)。
区间边着色的概念是由Asratian和Kamalian在 [1] [2] 中提出来的,并且证明了如果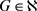 ,那么
,那么 。在 [3] 中,Kamalian证明了如果
。在 [3] 中,Kamalian证明了如果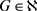 是一个连通图,那么
是一个连通图,那么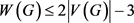 。这个上界被Giaro等在 [4] 中改进了,他们证明了如果
。这个上界被Giaro等在 [4] 中改进了,他们证明了如果 是一个至少有3个顶点的连通图,那么
是一个至少有3个顶点的连通图,那么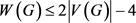 。对某些图类来说,
。对某些图类来说, 的上界还得到了进一步的改进,其中包括不含三角形的图 [1] [2] 和可平面图 [5] 。
的上界还得到了进一步的改进,其中包括不含三角形的图 [1] [2] 和可平面图 [5] 。
广义θ-图是由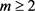 条两两内部不交的
条两两内部不交的 -路构成的简单图,记作
-路构成的简单图,记作 。广义θ-链是把路
。广义θ-链是把路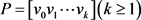 的每一条边
的每一条边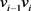 (
( )用
)用 条两两内部不交的
条两两内部不交的 -路替换掉得到的简单图,记作
-路替换掉得到的简单图,记作 。在本文中,我们给出了
。在本文中,我们给出了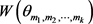 的一个紧的上界。
的一个紧的上界。
2. 的一个上界
的一个上界
令 ,
,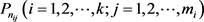 是
是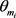 中两两内部不交的
中两两内部不交的 -路。对每一个
-路。对每一个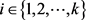 ,令
,令
 ,
, 
为了方便,我们记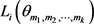 为
为 中第i大的数,
中第i大的数,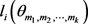 为
为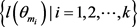 中第i大的数。
中第i大的数。
引理2.1:设α是可区间着色图G的一个区间t-着色,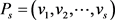 是G中的一条路,其中
是G中的一条路,其中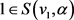 且
且 。那么
。那么 ,等号成立当且仅当
,等号成立当且仅当
 ,
,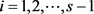 。
。
证明:因为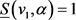 且
且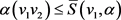 ,我们有
,我们有
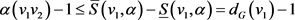 , (1)
, (1)
等号成立当且仅当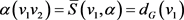 。因为
。因为 且
且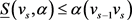 ,我们有
,我们有
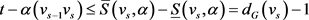 , (2)
, (2)
等号成立当且仅当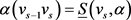 。因为
。因为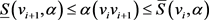 ,
,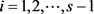 ,我们有
,我们有
 ,
, (3)
(3)
等号成立当且仅当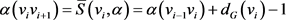 且
且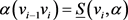 。
。
由(1)-(3),我们可以得到
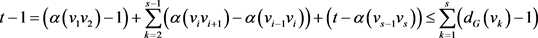 ,
,
等号成立当且仅当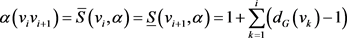 ,
,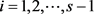 。
。
证毕。
定理2.3:若广义θ-链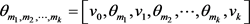 可区间边着色的,那么
可区间边着色的,那么
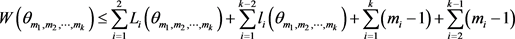 .
.
证明:设α是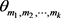 的一个区间
的一个区间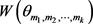 -着色。那么存在两条边
-着色。那么存在两条边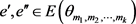 使得
使得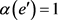 且
且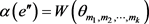 。我们分以下两种情况讨论。
。我们分以下两种情况讨论。
Case 1.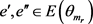 ,
, 。
。
首先,我们假设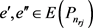 ,
,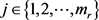 。令
。令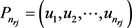 ,
,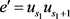 ,
,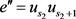 ,这里
,这里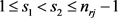 且
且 。那么
。那么 ,
,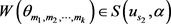 。由引理2.1,我们有
。由引理2.1,我们有
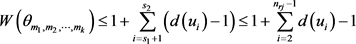 。 (4)
。 (4)
因为 且
且 ,由(4)我们有
,由(4)我们有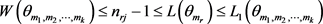 ,因此结论成立。
,因此结论成立。
其次,我们假设 且
且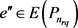 ,这里
,这里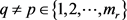 。设
。设 ,
,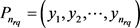 ,
,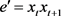 ,
,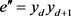 ,这里
,这里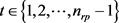 ,
,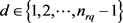 ,
, ,
, 。我们考虑以下两条路:
。我们考虑以下两条路:
 ,
,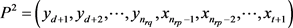 .
.
显然, ,因此
,因此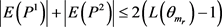 。我们能断言
。我们能断言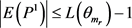 或者
或者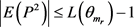 ,否则
,否则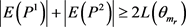 ,矛盾。不失一般性,设
,矛盾。不失一般性,设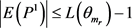 ,那么
,那么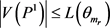 。注意到
。注意到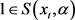 且
且 。由引理2.1,我们有
。由引理2.1,我们有
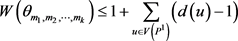 . (5)
. (5)
因为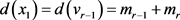 ,且对任意
,且对任意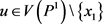 有
有 ,由(5),我们有
,由(5),我们有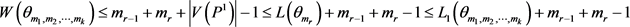 ,因此结论成立。
,因此结论成立。
Case 2.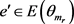 ,
, ,
, .
.
不失一般性,设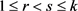 ,
,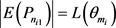 且
且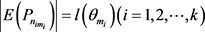 ,
,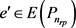 且
且 ,这里
,这里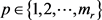 且
且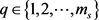 。设
。设 ,
, ,
, ,
,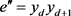 ,这里
,这里 ,
,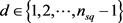 ,
,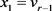 ,
,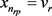 ,
,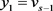 ,
,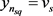 。那么
。那么
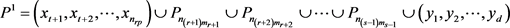
是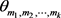 中的一条路满足
中的一条路满足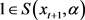 且
且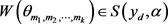 。由引理2.1,可得
。由引理2.1,可得
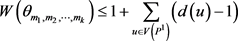 . (6)
. (6)
令

显然,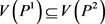 ,表明
,表明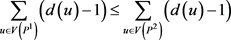 。因为
。因为
 ,且对任意
,且对任意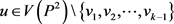 有
有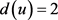 ,
,
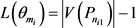 ,由(6),我们有
,由(6),我们有
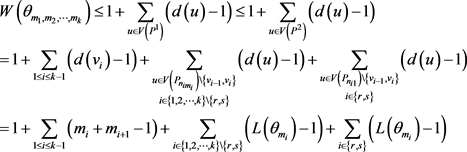
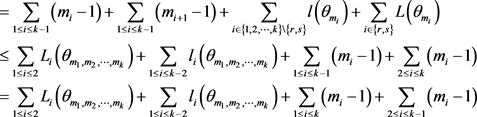
因此结论成立。
证毕。
文章引用
陈 勋. 广义θ-链的区间边着色的上界
The Upper Bound of the Interval Edge-Coloring of the Generalized θ-Chain[J]. 应用数学进展, 2018, 07(04): 418-422. https://doi.org/10.12677/AAM.2018.74052
参考文献
- 1. Asratian, A.S. and Kamalian, R.R. (1987) Interval Colorings of Edges of a Multigraph. Appl. Math., 5, 25-34. (In Russian)
- 2. Asratian, A.S. and Kamalian, R.R. (1994) Investigation on Interval Edge-Colorings of Graphs. Journal of Combinatorial Theory, Series B, 62, 34-43. https://doi.org/10.1006/jctb.1994.1053
- 3. Kamalian, R.R. (1990) Interval Edge Colorings of Graphs. Doctoral Thesis, Novosibirsk.
- 4. Giaro, K., Kubale, M. and MaLafiejski, M. (2001) Consecutive Colorings of the Edges of General Graphs. Discrete Mathematics, 239, 131-143. https://doi.org/10.1016/S0012-365X(00)00437-4
- 5. Axenovich, M.A. (2002) On Interval Colorings of Planar Graphs. Congressus Numerantium, 159, 77-94.