ABSTRACT

The transformation graph G^--- of a graph G is the graph with vertex set $V\left(G\right)\cup E\left(G\right)$ , in which two vertices u and v are joined by an edge if one of the following conditions holds: 1) $u,v\in V\left(G\right)$ and they are not adjacent in G, 2) $u,v\in E\left(G\right)$ and they are not adjacent in G, 3) one of u and v is in $V\left(G\right)$ while the other is in $E\left(G\right)$ , and they are not incident in G. The Wiener index $W\left(G\right)$ of G is the sum of the distances between all pairs of vertices in G. In this note, for any graph G, we determine the Wiener index of G^---, when G^--- is connected.

Keywords:Transformation Graph, Wiener Index

变换图G^---的Wiener指标

赵艳华

新疆大学，数学与系统科学学院，新疆 乌鲁木齐

收稿日期：2019年4月3日；录用日期：2019年4月18日；发布日期：2019年4月25日

摘 要

图G的变换图G^---的顶点集为 $V\left(G\right)\cup E\left(G\right)$ ，图G^---中任意两顶点 $u,v\in V\left(G^{---}\right)$ 只需满足下面任意一个条件便可以连边：1) $u,v\in V\left(G\right)$ ，它们在图G中不相邻，2) $u,v\in E\left(G\right)$ ，它们在图G中不相邻，3) $u\in V\left(G\right)$ ， $v\in E\left(G\right)$ ，它们在图G中不关联。图G的Wiener指标是图G中所有点对的距离之和。在本文中，我们确定了变换图G^---是连通图时的Wiener指标。

关键词 :变换图，Wiener指标

Copyright © 2019 by author and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

本篇文章中所有的图都为无向的简单图。所用到的符号和术语参考文献 [1] 。设简单图 $G$ 的顶点集为 $V\left(G\right)$ ，图 $G$ 的边集为 $E\left(G\right)$ 。对于 $V\left(G\right)$ 中的任意顶点 $v$ ，我们记 $N_G\left(v\right)$ 为图 $G$ 中所有和顶点 $v$ 相邻的顶点的集合。称 $d_G\left(v\right)=\left|N_G\left(v\right)\right|$ 为顶点 $v$ 的度数。

在一个连通图 $G$ 中，用 $d_G\left(u,v\right)$ 表示 $G$ 中任意两个顶点u和v之间的距离(两点之间最短路的长度)，图 $G$ 的Wiener指标是指图 $G$ 中所有顶点对的距离之和，即 $W\left(G\right)={\displaystyle \underset{u,v\in V\left(G\right)}{\sum }{d}_G}\left(u,v\right)$ 。在不引起歧义的情况下，我们把 $d_G\left(v\right)$ ， $d_G\left(u,v\right)$ 分别简记为 $d\left(v\right)$ ， $d\left(u,v\right)$ 。

这个概念最初是由Harry Wiener在1947年的文献 [2] 中提到的，之后作为一个重要的拓扑指标应用于化学研究中，用来研究分子的结构。后来Entringer等人在1976年文献 [3] 中首次引入到数学领域，引起许多数学家的兴趣。关于一些Wiener指标的化学应用和数学研究的调查可以参考文献 [4] 以及其中引用的参考资料。

吴和孟在文献 [5] 中给出了全变换图的基本性质。我们可以在文献 [6] [7] [8] 中查阅到变换图的更多结果。

在本文中，我们将根据吴和孟的结果确定连通的变换图 $G^{\text{---}}$ 的Wiener指标。

2. 主要内容

2.1. 预备知识

在文献 [5] 中吴和孟给出了下面的结果。

定理2.1.1： [5] 如果图 $G$ 既不是星图也不是三角形，则 $\text{diam}\left(G^{---}\right)\le 3$ 。

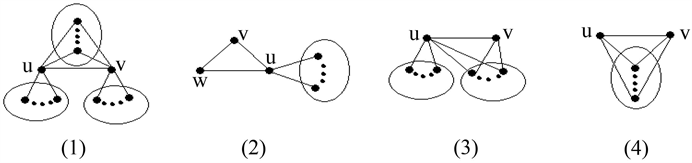
当图 $G$ 是星图或者是三角形的时候，图 $G^{\text{---}}$ 是不连通的。由定理2.1.1的证明过程可知，当 $u,v\in V\left(G\right)$ 时， $d\left(u,v\right)\le 3$ ；当 $u,v\in E\left(G\right)$ 时， $d\left(u,v\right)\le 2$ ；当 $u\in V\left(G\right),v\in E\left(G\right)$ 时， $d\left(u,v\right)\le 3$ 。而且当 $\text{diam}\left(G^{---}\right)=3$ ，我们有图 $G$ 的结构(如图1所示)。

如图1(1)中，在其变换图中距离是3的顶点对为 $u,v$ ；如图1(2)中，在其变换图中距离是3的顶点对为 $u,v$ 、 $u,w$ 、 $u,uv$ 及 $u,uw$ ；如图1(3)中，在其变换图中距离是3的顶点对为 $u,v$ 、 $u,uv$ ；如图1(4)中，在其变换图中距离是3的顶点对为 $u,v$ 、 $u,uv$ 及 $v,vu$ 。

在本文，我们主要根据上面直径求变换图 $G^{---}$ 的Wiener指标。

2.2. 直径小于等于2

当顶点 $u$ 和边 $e$ 关联时，我们记为 $m_{ue}=1$ ，当边 $e,f$ 相邻时记为 $m_{ef}=1$ 。否则，我们分别记为 $m_{uv}=0$ ， $m_{ef}=0$ 。

图1. $\text{diam}\left(G^{---}\right)=3$

定理2.2.1：如果图 $G$ 的顶点的阶数为 $n$ ，边的阶数为 $m$ ，且 $\text{diam}\left(G^{---}\right)\le 2$ ，则

$W\left(G^{---}\right)=\frac{1}{2}\left(m^2+n^2+{\displaystyle \underset{v\in V\left(G\right)}{\sum }{d}_G^2}\left(v\right)\right)+mn+\frac{3}{2}m-\frac{1}{2}n.$

证明：记 $u,v$ 为图 $G$ 中任意两个顶点， $e,f$ 为图 $G$ 中任意两条边， $V\left(G^{---}\right)=\left\{u_1,u_2,\cdots u_{m+n}\right\}$ 。在图 $G$ 相邻边的个数为 ${\displaystyle \underset{v\in V\left(G\right)}{\sum }\left(\begin{array}{c}{d}_G\left(v\right)\\ 2\end{array}\right)}$ ，又因为 $\text{diam}\left(G^{---}\right)\le 2$ ，所以对于任意的点 $u_1,u_2\in V\left(G^{---}\right)$ ， $u_1$ 和 $u_2$ 之间的距离为1或2。因此，由Wiener指标的定义可知：

$\begin{array}{c}W\left(G^{---}\right)={\displaystyle \underset{u,v}{\sum }{d}_{G^{---}}\left(u,v\right)}+{\displaystyle \underset{u,e}{\sum }{d}_{G^{---}}\left(u,e\right)}+{\displaystyle \underset{e,f}{\sum }{d}_{G^{---}}\left(e,f\right)}\\ =\left({\displaystyle \underset{uv\notin E\left(G\right)}{\sum }{d}_{G^{---}}\left(u,v\right)}+{\displaystyle \underset{uv\in E\left(G\right)}{\sum }{d}_{G^{---}}\left(u,v\right)}\right)+\left({\displaystyle \underset{m_{ue}=0}{\sum }{d}_{G^{---}}\left(u,e\right)}+{\displaystyle \underset{m_{ue}=1}{\sum }{d}_{G^{---}}\left(u,e\right)}\right)\\ +\left({\displaystyle \underset{m_{ef}=0}{\sum }{d}_{G^{---}}\left(e,f\right)}+{\displaystyle \underset{m_{ef}=1}{\sum }{d}_{G^{---}}\left(e,f\right)}\right)\\ =\left(\left(\begin{array}{c}n\\ 2\end{array}\right)-m+2m\right)+\left(mn-2m+4m\right)+\left(\left(\begin{array}{c}m\\ 2\end{array}\right)-{\displaystyle \underset{v\in V\left(G\right)}{\sum }\left(\begin{array}{c}{d}_G\left(v\right)\\ 2\end{array}\right)+2{\displaystyle \underset{v\in V\left(G\right)}{\sum }\left(\begin{array}{c}{d}_G\left(v\right)\\ 2\end{array}\right)}}\right)\\ =\frac{1}{2}\left(m^2+n^2+{\displaystyle \underset{v\in V\left(G\right)}{\sum }{d}_G^2\left(v\right)}\right)+mn+\frac{3}{2}m-\frac{1}{2}n.\end{array}$

2.3. 直径等于3

定理2.3.1：如果图 $G$ 的边数为 $m$ ，顶点数为 $n$ ，当 $\text{diam}\left(G^{---}\right)=3$ 时，则具有图1四类图中的某一种结构，且对应的Wiener指标分别为

1) $W\left(G^{---}\right)=\frac{1}{2}\left(m^2+n^2+{\displaystyle \underset{v\in V\left(G\right)}{\sum }{d}_G^2}\left(v\right)\right)+mn+\frac{3}{2}m-\frac{1}{2}n+1$

2) $W\left(G^{---}\right)=\frac{1}{2}\left(m^2+n^2+{\displaystyle \underset{v\in V\left(G\right)}{\sum }{d}_G^2}\left(v\right)\right)+mn+\frac{3}{2}m-\frac{1}{2}n+4$

3) $W\left(G^{---}\right)=\frac{1}{2}\left(m^2+n^2+{\displaystyle \underset{v\in V\left(G\right)}{\sum }{d}_G^2}\left(v\right)\right)+mn+\frac{3}{2}m-\frac{1}{2}n+2$

4) $W\left(G^{---}\right)=\frac{1}{2}\left(m^2+n^2+{\displaystyle \underset{v\in V\left(G\right)}{\sum }{d}_G^2}\left(v\right)\right)+mn+\frac{3}{2}m-\frac{1}{2}n+3$

证明：首先由定理2.1.1的证明可以知道，直径可以达到3的变换图 $G^{---}$ 的原图 $G$ 的结构只有图1中四种结构。下面分别给出它们的Wiener指标。

对于图1(1)，容易看出图 $G^{---}$ 中距离是3的点对只有 $u,v$ 。从而

$\begin{array}{c}W\left(G^{---}\right)={\displaystyle \underset{u,v}{\sum }{d}_{G^{---}}\left(u,v\right)}+{\displaystyle \underset{u,e}{\sum }{d}_{G^{---}}\left(u,e\right)}+{\displaystyle \underset{e,f}{\sum }{d}_{G^{---}}\left(e,f\right)}\\ =\left({\displaystyle \underset{uv\notin E\left(G\right)}{\sum }{d}_{G^{---}}\left(u,v\right)}+{\displaystyle \underset{uv\in E\left(G\right)}{\sum }{d}_{G^{---}}\left(u,v\right)}\right)+\left({\displaystyle \underset{m_{ue}=0}{\sum }{d}_{G^{---}}\left(u,e\right)}+{\displaystyle \underset{m_{ue}=1}{\sum }{d}_{G^{---}}\left(u,e\right)}\right)\\ +\left({\displaystyle \underset{m_{ef}=0}{\sum }{d}_{G^{---}}\left(e,f\right)}+{\displaystyle \underset{m_{ef}=1}{\sum }{d}_{G^{---}}\left(e,f\right)}\right)\\ =\left(\left(\begin{array}{c}n\\ 2\end{array}\right)-m+2\left(m-1\right)+3\right)+\left(mn-2m+4m\right)+\left(\left(\begin{array}{c}m\\ 2\end{array}\right)-{\displaystyle \underset{v\in V\left(G\right)}{\sum }\left(\begin{array}{c}{d}_G\left(v\right)\\ 2\end{array}\right)+2{\displaystyle \underset{v\in V\left(G\right)}{\sum }\left(\begin{array}{c}{d}_G\left(v\right)\\ 2\end{array}\right)}}\right)\\ =\frac{1}{2}\left(m^2+n^2+{\displaystyle \underset{v\in V\left(G\right)}{\sum }{d}_G^2\left(v\right)}\right)+mn+\frac{3}{2}m-\frac{1}{2}n+1.\end{array}$

对于图1(2)，容易看出图 $G^{---}$ 中距离是3的顶点对为 $u,v$ ； $u,w$ ； $u,uv$ 及 $u,uw$ 。从而

$\begin{array}{c}W\left(G^{---}\right)={\displaystyle \underset{u,v}{\sum }{d}_{G^{---}}\left(u,v\right)}+{\displaystyle \underset{u,e}{\sum }{d}_{G^{---}}\left(u,e\right)}+{\displaystyle \underset{e,f}{\sum }{d}_{G^{---}}\left(e,f\right)}=\left({\displaystyle \underset{uv\notin E\left(G\right)}{\sum }{d}_{G^{---}}\left(u,v\right)}+{\displaystyle \underset{uv\in E\left(G\right)}{\sum }{d}_{G^{---}}\left(u,v\right)}\right)\\ +\left({\displaystyle \underset{m_{ue}=0}{\sum }{d}_{G^{---}}\left(u,e\right)}+{\displaystyle \underset{m_{ue}=1}{\sum }{d}_{G^{---}}\left(u,e\right)}\right)+\left({\displaystyle \underset{m_{ef}=0}{\sum }{d}_{G^{---}}\left(e,f\right)}+{\displaystyle \underset{m_{ef}=1}{\sum }{d}_{G^{---}}\left(e,f\right)}\right)\\ =\left(\left(\begin{array}{c}n\\ 2\end{array}\right)-m+2\left(m-2\right)+3\times 2\right)+\left(mn-2m+2\left(2m-2\right)+3\times 2\right)\\ +\left(\left(\begin{array}{c}m\\ 2\end{array}\right)-{\displaystyle \underset{v\in V\left(G\right)}{\sum }\left(\begin{array}{c}{d}_G\left(v\right)\\ 2\end{array}\right)+2{\displaystyle \underset{v\in V\left(G\right)}{\sum }\left(\begin{array}{c}{d}_G\left(v\right)\\ 2\end{array}\right)}}\right)\\ =\frac{1}{2}\left(m^2+n^2+{\displaystyle \underset{v\in V\left(G\right)}{\sum }{d}_G^2\left(v\right)}\right)+mn+\frac{3}{2}m-\frac{1}{2}n+4.\end{array}$

对于图1(3)，容易看出图 $G^{---}$ 中距离是3的顶点对为 $u,v$ 和 $u,uv$ 。从而

$\begin{array}{c}W\left(G^{---}\right)={\displaystyle \underset{u,v}{\sum }{d}_{G^{---}}\left(u,v\right)}+{\displaystyle \underset{u,e}{\sum }{d}_{G^{---}}\left(u,e\right)}+{\displaystyle \underset{e,f}{\sum }{d}_{G^{---}}\left(e,f\right)}\\ =\left({\displaystyle \underset{uv\notin E\left(G\right)}{\sum }{d}_{G^{---}}\left(u,v\right)}+{\displaystyle \underset{uv\in E\left(G\right)}{\sum }{d}_{G^{---}}\left(u,v\right)}\right)\\ +\left({\displaystyle \underset{m_{ue}=0}{\sum }{d}_{G^{---}}\left(u,e\right)}+{\displaystyle \underset{m_{ue}=1}{\sum }{d}_{G^{---}}\left(u,e\right)}\right)+\left({\displaystyle \underset{m_{ef}=0}{\sum }{d}_{G^{---}}\left(e,f\right)}+{\displaystyle \underset{m_{ef}=1}{\sum }{d}_{G^{---}}\left(e,f\right)}\right)\\ =\left(\left(\begin{array}{c}n\\ 2\end{array}\right)-m+2\left(m-1\right)+3\right)+\left(mn-2m+2\left(2m-1\right)+3\right)+\left(\left(\begin{array}{c}m\\ 2\end{array}\right)-{\displaystyle \underset{v\in V\left(G\right)}{\sum }\left(\begin{array}{c}{d}_G\left(v\right)\\ 2\end{array}\right)+2{\displaystyle \underset{v\in V\left(G\right)}{\sum }\left(\begin{array}{c}{d}_G\left(v\right)\\ 2\end{array}\right)}}\right)\\ =\frac{1}{2}\left(m^2+n^2+{\displaystyle \underset{v\in V\left(G\right)}{\sum }{d}_G^2\left(v\right)}\right)+mn+\frac{3}{2}m-\frac{1}{2}n+2.\end{array}$

对于图1(4)，容易看出图 $G^{---}$ 中距离是3的顶点对为 $u,v$ ； $u,uv$ 及 $v,vu$ 。从而

$\begin{array}{c}W\left(G^{---}\right)={\displaystyle \underset{u,v}{\sum }{d}_{G^{---}}\left(u,v\right)}+{\displaystyle \underset{u,e}{\sum }{d}_{G^{---}}\left(u,e\right)}+{\displaystyle \underset{e,f}{\sum }{d}_{G^{---}}\left(e,f\right)}\\ =\left({\displaystyle \underset{uv\notin E\left(G\right)}{\sum }{d}_{G^{---}}\left(u,v\right)}+{\displaystyle \underset{uv\in E\left(G\right)}{\sum }{d}_{G^{---}}\left(u,v\right)}\right)+\left({\displaystyle \underset{m_{ue}=0}{\sum }{d}_{G^{---}}\left(u,e\right)}+{\displaystyle \underset{m_{ue}=1}{\sum }{d}_{G^{---}}\left(u,e\right)}\right)\\ +\left({\displaystyle \underset{m_{ef}=0}{\sum }{d}_{G^{---}}\left(e,f\right)}+{\displaystyle \underset{m_{ef}=1}{\sum }{d}_{G^{---}}\left(e,f\right)}\right)\\ =\left(\left(\begin{array}{c}n\\ 2\end{array}\right)-m+2\left(m-1\right)+3\right)+\left(mn-2m+2\left(2m-2\right)+3\times 2\right)+\left(\left(\begin{array}{c}m\\ 2\end{array}\right)-{\displaystyle \underset{v\in V\left(G\right)}{\sum }\left(\begin{array}{c}{d}_G\left(v\right)\\ 2\end{array}\right)+2{\displaystyle \underset{v\in V\left(G\right)}{\sum }\left(\begin{array}{c}{d}_G\left(v\right)\\ 2\end{array}\right)}}\right)\\ =\frac{1}{2}\left(m^2+n^2+{\displaystyle \underset{v\in V\left(G\right)}{\sum }{d}_G^2\left(v\right)}\right)+mn+\frac{3}{2}m-\frac{1}{2}n+3.\end{array}$

文章引用

赵艳华. 变换图G---的Wiener指标
Wiener Index of Transformation Graph G---[J]. 应用数学进展, 2019, 08(04): 703-707. https://doi.org/10.12677/AAM.2019.84080

参考文献