Advances in Applied Mathematics
Vol.
09
No.
03
(
2020
), Article ID:
34686
,
8
pages
10.12677/AAM.2020.93048
Extinction of the Density Dependent Nonautonomous Predator-Prey System with Beddington-DeAngelis Functional Response
Wenrui Zeng, Dingyong Bai, Jinshui Li
School of Mathematics and Information Science, Guangzhou University, Guangzhou Guangdong

Received: Mar. 1st, 2020; accepted: Mar. 16th, 2020; published: Mar. 24th, 2020

ABSTRACT
In this paper, the density dependent nonautonomous predator-prey system with Beddington-DeAngelis functional response is studied. The global asymptotic stability of boundary periodic solution is obtained by using the comparison theorem, differential inequality and the dynamics of Logistic equation. Our main result indicates that, even though there is no intraspecific competition, over a periodic interval if the average predation benefit is less than the average death number of predator species, the predator species will go extinction. In addition, some numerical simulations are performed to illustrate the theoretical results.
Keywords:Beddington-DeAngelis Functional Response, Nonautonomous Predator-Prey System, Global Asymptotic Stability, Boundary Periodic Solution, Extinction

具有Beddington-DeAngelis功能反应 和密度制约的非自治捕食–食饵系统的灭绝性
曾文瑞,白定勇,李金水
广州大学数学与信息科学学院,广东 广州

收稿日期:2020年3月1日;录用日期:2020年3月16日;发布日期:2020年3月24日

摘 要
本文研究具有Beddington-DeAngelis功能反应和密度制约的非自治捕食–食饵系统,利用比较定理和微分不等式及Logistic方程的动力学行为,得到边界周期解的全局渐近稳定性。我们的主要结论表明,即使没有种内竞争,但如果在一个周期区间上捕食者种群的平均收益小于平均死亡数,就会导致该种群的灭绝。另外,给出了数值模拟验证所得理论结果是正确的。
关键词 :Beddington-DeAngelis功能反应,非自治捕食–食饵系统,全局渐近稳定性,边界周期解,灭绝

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
捕食–食饵系统的动力学分析是生物数学研究中的热点问题。在捕食–食饵系统中,捕食者的功能反应对系统的动力学行为有着重要影响。常见的功能反应类型有:Holling I-IV型,比率依赖型,Michaelis-Menten型,Beddington-DeAngelis型以及Hassell-Varley型等(参见文 [1] - [7] )。Skalski [8] 等学者从大量捕食–食饵系统中得到的统计数据表明,在某些条件下Beddington-DeAngelis型功能反应
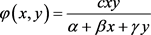 能更好地体现捕食者与捕食–食饵系统中各个生物参量之间的关系。这类模型不仅
能更好地体现捕食者与捕食–食饵系统中各个生物参量之间的关系。这类模型不仅
具有Holling-II型( 时)功能反应的特点,而且具有比率依赖型(
时)功能反应的特点,而且具有比率依赖型( 时)功能反应的特性。Beddington [9] 和DeAngelis等 [10] 最早分别独立提出具有Beddington-DeAngelis型功能反应的捕食–食饵模型
时)功能反应的特性。Beddington [9] 和DeAngelis等 [10] 最早分别独立提出具有Beddington-DeAngelis型功能反应的捕食–食饵模型
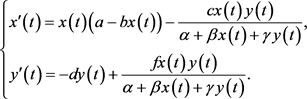
其中, 分别表示在t时刻食饵和捕食种群的密度,所有的参数都是正常数,a是食饵种群的内禀增长率,
分别表示在t时刻食饵和捕食种群的密度,所有的参数都是正常数,a是食饵种群的内禀增长率,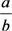 表示食饵种群的环境容纳量,捕食种群以Beddington-DeAngelis型
表示食饵种群的环境容纳量,捕食种群以Beddington-DeAngelis型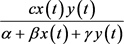 的功能反应捕食食饵,并且以
的功能反应捕食食饵,并且以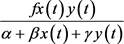 的速率促进其自身的繁殖或者生长。近年来具有Beddington-DeAngelis型
的速率促进其自身的繁殖或者生长。近年来具有Beddington-DeAngelis型
功能反应的生物模型得到了许多学者广泛的研究,例如,文献 [11] [12] [13] 研究了这类系统的平衡点、全局吸引子和极限环等动力学性质,但这些理论结果都是在常数环境下得到的。在实际的生态环境下,出生率、死亡率和其它生物参数都会随时间变化,因此非常有必要研究相应的非自治系统。
Fan和Kuang [5] 研究了具有Beddington-DeAngelis型功能反应的非自治捕食–食饵系统
 (1)
(1)
文 [5] 研究了系统(1)的持久性、灭绝性和全局渐近稳定性,在周期参数情形下,得到了正周期解存在性条件及边界周期解全局渐近稳定的充分条件。文 [14] 进一步研究了系统(1)的持久性,给出了新的正周期解存在性条件,改进了文献 [5] 中的理论结果。文 [6] 利用波动引理,证明了系统(1)边界解的全局渐近稳定性,得到积分形式的充分条件,推广了文 [5] 的结果。我们注意到,在文 [5] 中除了允许参数 是非负连续函数外,其余参数均要求有正的下界,而在文 [6] 中要求所有的参数有正的下界。在文 [14] 中,要求参数
是非负连续函数外,其余参数均要求有正的下界,而在文 [6] 中要求所有的参数有正的下界。在文 [14] 中,要求参数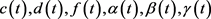 均是正值连续函数。然而在实际的自然环境中,生物参数的下确界可能为零,甚至于允许变号。比如,捕食者可能在某些时刻捕获不到食物,从而在该时刻参数
均是正值连续函数。然而在实际的自然环境中,生物参数的下确界可能为零,甚至于允许变号。比如,捕食者可能在某些时刻捕获不到食物,从而在该时刻参数 。考虑到在实际的生态环境中,种群在某些时刻的自然出生率可能小于死亡率,那么在该时刻的内禀增长率
。考虑到在实际的生态环境中,种群在某些时刻的自然出生率可能小于死亡率,那么在该时刻的内禀增长率 可能为负,在这种情况下,文 [6] 采用的方法将不能适用。
可能为负,在这种情况下,文 [6] 采用的方法将不能适用。
由于捕食者之间存在着内部竞争,那么有必要考虑捕食种群内部具有密度制约项的模型。Li和Takeuchi [7] 研究了捕食种群具有密度制约和Beddington-DeAngelis功能反应的非自治捕食–食饵系统
 (2)
(2)
周期情形下,文 [7] 得到如下灭绝性条件
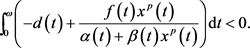 (3)
(3)
此外,利用Lyapunov函数,得到如下边界周期解的全局渐近稳定性条件
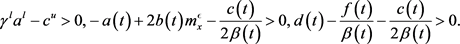 (4)
(4)
其中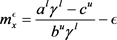 ,
, 是充分小实数。其中,
是充分小实数。其中,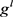 和
和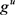 分别表示定义在
分别表示定义在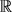 上有界连续函数
上有界连续函数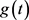 的下、上确界。
的下、上确界。
文 [7] 中要求所有的参数有正的下界。条件(3)事实上是文 [6] 得到的边界周期解全局稳定性条件,而文 [7] 得到的全局稳定性条件(4)很难给出恰当的生物解释。
本文在周期参数情形下,利用比较定理和微分不等式以及Logistic方程解的性质,研究系统(2)边界周期解的全局渐近稳定性,推广文 [7] 中的相应结论。当 时,也推广了文 [6] 中的结果。另外,我们将利用数值模拟验证所得到的理论结果。
时,也推广了文 [6] 中的结果。另外,我们将利用数值模拟验证所得到的理论结果。
考虑到生物意义,本文只考虑系统(2)过正初始值 的解
的解 。
。
2. 主要结果
我们假设所有的参数是定义在 上连续的
上连续的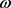 -周期函数,其中,
-周期函数,其中,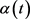 有正的下界,
有正的下界,
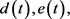
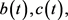 非负,讨论系统(2)边界周期解的全局渐近稳定性。
非负,讨论系统(2)边界周期解的全局渐近稳定性。
定义2.1:设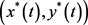 是系统(2)的一个有界非负解,若系统(2)过正初始值的任意解
是系统(2)的一个有界非负解,若系统(2)过正初始值的任意解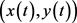 满足
满足
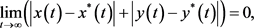
则称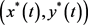 是全局渐近稳定(全局吸引)的。
是全局渐近稳定(全局吸引)的。
下面的结论是显然的。
定理2.2: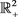 是系统(2)的正不变集。
是系统(2)的正不变集。
对连续的 -周期函数
-周期函数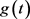 ,用
,用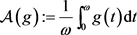 表示函数
表示函数 在一个周期区间上的平均值。考虑Logistic方程
在一个周期区间上的平均值。考虑Logistic方程
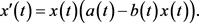 (5)
(5)
引理2.3: [15] 设 且
且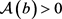 ,则方程(5)有唯一非负的
,则方程(5)有唯一非负的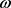 -周期解
-周期解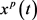 全局渐近稳定,即方程(5)满足正初始值的任意解
全局渐近稳定,即方程(5)满足正初始值的任意解 ,都有
,都有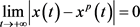 。进一步,若
。进一步,若 ,则
,则 ;若
;若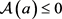 ,则
,则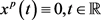 。
。
注 可以写成如下形式(参见文 [16] )
可以写成如下形式(参见文 [16] )
 (6)
(6)
由引理2.3,若 ,
, ,则系统(2)存在边界
,则系统(2)存在边界 -周期解
-周期解 。为方便起见,定义
。为方便起见,定义
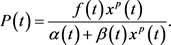
下面,我们给出本文的主要结果。
定理2.4:设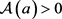 ,
,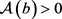 。若
。若 ,则系统(2)的边界周期解
,则系统(2)的边界周期解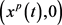 是全局渐近稳定的。
是全局渐近稳定的。
证明:由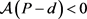 成立,则可选取
成立,则可选取 充分小,使得
充分小,使得
 (7)
(7)
设 是系统(2)的任一正解,
是系统(2)的任一正解, 是方程(5)满足初始条件
是方程(5)满足初始条件 的解。由系统(2)的第一个方程及比较定理我们有
的解。由系统(2)的第一个方程及比较定理我们有 。由引理2.3,有
。由引理2.3,有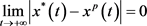 。则对上述
。则对上述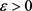 ,存在
,存在 ,当
,当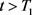 时,有
时,有
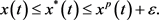 (8)
(8)
因此,当 时,由系统(2)的第二个方程,有
时,由系统(2)的第二个方程,有

则当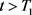 时,
时,
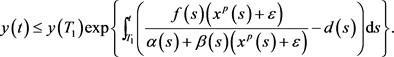
所以,由(7),得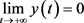 。
。
下证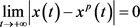 。由
。由 ,可选取充分小
,可选取充分小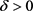 ,使得
,使得
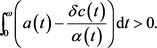 (9)
(9)
考虑方程
 (10)
(10)
由(9)及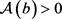 ,根据引理2.3知方程(10)存在全局渐近稳定的正解
,根据引理2.3知方程(10)存在全局渐近稳定的正解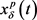 。设
。设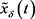 是方程(10)满足
是方程(10)满足 的解,则
的解,则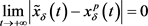 。那么,存在
。那么,存在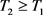 ,使得当
,使得当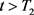 时,
时,
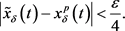
由解对参数的连续依赖性定理,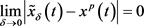 对
对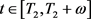 一致成立。则存在
一致成立。则存在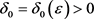 ,使得
,使得
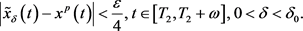
于是,
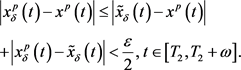
由于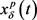 ,
, 都是
都是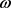 周期函数,得
周期函数,得
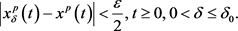
选取常数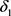 ,满足
,满足 且
且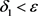 ,则
,则
 (11)
(11)
由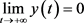 可知,存在
可知,存在 ,使得当
,使得当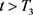 时,
时,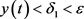 。由系统(2)的第一个方程,有
。由系统(2)的第一个方程,有
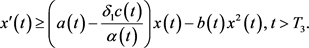
由比较定理知 ,其中,
,其中,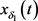 是方程(10)满足
是方程(10)满足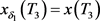 的解。由于
的解。由于 全局稳定,则存在
全局稳定,则存在 ,使得当
,使得当 时,
时,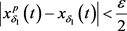 。于是
。于是
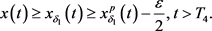 (12)
(12)
所以,由(11)和(12),得
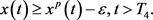 (13)
(13)
这样,由(13)和(8),得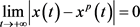 。因此,边界周期解
。因此,边界周期解 全局渐近稳定。
全局渐近稳定。
注:
1) 如果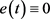 ,定理2.4仍然成立,条件
,定理2.4仍然成立,条件 与文 [6] 给出的一致,但文 [6] 要求
与文 [6] 给出的一致,但文 [6] 要求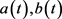 都有正的下界,而本文定理2.4允许
都有正的下界,而本文定理2.4允许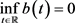 ,且
,且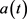 允许改变符号。在本文的假设条件下无法应用文 [6] 采用的方法来证明边界周期解的全局稳定性。
允许改变符号。在本文的假设条件下无法应用文 [6] 采用的方法来证明边界周期解的全局稳定性。
2) 生物解释:定理2.4表明,即使没有种内竞争(即 ),但如果在一个周期区间上捕食者种群的平均收益小于平均死亡数(即
),但如果在一个周期区间上捕食者种群的平均收益小于平均死亡数(即 ),就会导致该种群灭绝。
),就会导致该种群灭绝。
3. 数值模拟
本节通过数值模拟对上述得到的理论结果进行验证。
例3.1:取参数

则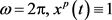 。显然,除了
。显然,除了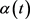 ,其余参数均非负,
,其余参数均非负, 。容易计算
。容易计算
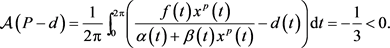
根据定理2.4,边界周期解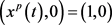 全局渐近稳定(见图1)。在图1中,初值取
全局渐近稳定(见图1)。在图1中,初值取

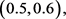 。
。

Figure 1. Global asymptotical stability of periodic 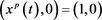 boundary solution of system (2)
boundary solution of system (2)
图1. 系统(2)的边界周期解 全局渐近稳定
全局渐近稳定
例3.2:取参数
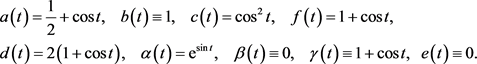
则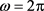 。显然,
。显然,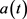 是变号的周期函数,但
是变号的周期函数,但 。因此,系统(2)存在边界周期解
。因此,系统(2)存在边界周期解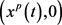 。由于
。由于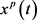 有下面形式
有下面形式

我们无法得到边界周期解的具体解析表达式。对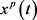 做估计,由
做估计,由
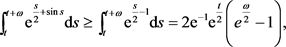
我们得到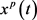 的估计式
的估计式 ,所以
,所以
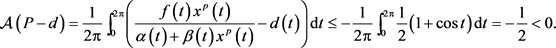
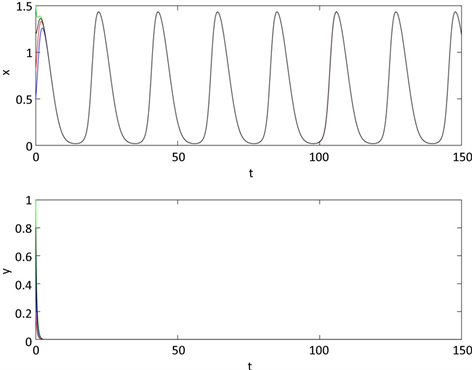
Figure 2. Global asymptotical stability of periodic 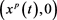 boundary solution of system (2)
boundary solution of system (2)
图2. 系统(2)的边界周期解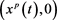 全局渐近稳定
全局渐近稳定
因此,根据定理2.4,系统(2)的边界周期解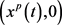 全局渐近稳定(见图2)。在图2中,初值取
全局渐近稳定(见图2)。在图2中,初值取
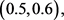 。
。
文章引用
曾文瑞,白定勇,李金水. 具有Beddington-DeAngelis功能反应和密度制约的非自治捕食–食饵系统的灭绝性
Extinctionof the Density Dependent Nonautonomous Predator-Prey System with Beddington-DeAngelis Functional Response[J]. 应用数学进展, 2020, 09(03): 400-407. https://doi.org/10.12677/AAM.2020.93048
参考文献
- 1. Yan, C.N., Dong, L.Z. and Liu, M. (2015) The Dynamical Behaviors of a Nonautonomous Holling III Predator-Prey System with Impulses. Journal of Applied Mathematics and Computing, 47, 193-209. https://doi.org/10.1007/s12190-014-0769-2
- 2. Li, Z., Chen, L. and Huang, J. (2009) Permanence and Periodicity of a Delayed Ratio-Dependent Predator-Prey Model with Holling Type Functional Response and Stage Structure. Journal of Applied Mathematics and Computing, 233, 173-187. https://doi.org/10.1016/j.cam.2009.07.008
- 3. Xu, R. and Chaplain, M.A.J. (2002) Persistence and Global Stability in a Delayed Predator-Prey System with Michaelis-Menten Type Functional Response. Applied Mathematics and Computation, 130, 441-455. https://doi.org/10.1016/S0096-3003(01)00111-4
- 4. Li, H. and She, Z. (2015) Uniqueness of Periodic Solutions of a Nonautonomous Density-Dependent Predator-Prey System. Journal of Mathematical Analysis and Applications, 422, 886-905. https://doi.org/10.1016/j.jmaa.2014.09.008
- 5. Fan, M. and Kuang, Y. (2004) Dynamics of a Nonautonomous Predator-Prey System with the Beddington-DeAngelis Functional Response. Journal of Mathematical Analysis and Applications, 295, 15-39. https://doi.org/10.1016/j.jmaa.2004.02.038
- 6. Chen, F., Chen, Y. and Shi, J. (2008) Stability of the Boundary Solution of a Nonautonomous Predator-Prey System with the Beddington-DeAngelis Functional Response. Journal of Mathematical Analysis and Applications, 344, 1057-1067. https://doi.org/10.1016/j.jmaa.2008.03.050
- 7. Li, H. and Takeuchi, Y. (2011) Dynamics of the Density Dependent Predator-Prey System with the Beddington-DeAngelis Functional Response. Journal of Mathematical Analysis and Applications, 374, 644-654. https://doi.org/10.1016/j.jmaa.2010.08.029
- 8. Skalski, G.T. and Gilliam, J.F. (2001) Functional Responses with Predator Interference: Viable Alternatives to the Holling Type II Model. Ecology, 82, 3083-3092. https://doi.org/10.1890/0012-9658(2001)082[3083:FRWPIV]2.0.CO;2
- 9. Beddington, J.R. (1975) Mutual In-terference between Parasites or Predators and Its Effect on Searching Efficiency. Journal of Animal Ecology, 44, 331-340. https://doi.org/10.2307/3866
- 10. DeAngelis, D.L., Goldstein, R.A. and Neill, R.V. (1975) A Model for Tropic Interaction. Ecology, 56, 67-68. https://doi.org/10.2307/1936298
- 11. Hwang, T.W. (2003) Global Analysis of the Predator-Prey System with Beddington-DeAngelis Functional Response. Journal of Mathematical Analysis and Applications, 281, 395-401. https://doi.org/10.1016/S0022-247X(02)00395-5
- 12. Hwang, T.W. (2004) Uniqueness of Limit Cycles of the Predator-Prey System with Beddington-DeAngelis Functional Response. Journal of Mathematical Analysis and Appli-cations, 290, 113-122. https://doi.org/10.1016/j.jmaa.2003.09.073
- 13. Cantrel, R.S. and Cosner, C. (2001) On the Dynamics of Preda-tor-Prey Models with the Beddington-DeAngelis Functional Response. Journal of Mathematical Analysis and Applica-tions, 257, 206-222. https://doi.org/10.1006/jmaa.2000.7343
- 14. Cui, J. and Takeuchi, Y. (2006) Permanence, Extinction and Periodic Solution of Predator-Prey System with Beddington-DeAngelis Functional Response. Journal of Mathematical Analysis and Applications, 317, 464-474. https://doi.org/10.1016/j.jmaa.2005.10.011
- 15. Tineo, A. (1995) An Iteretive Scheme for the N-Competing Spe-cies Problem. Journal of Differential Equations, 116, 1-15. https://doi.org/10.1006/jdeq.1995.1026
- 16. Fan, M. and Wang, K. (1998) Optimal Harvesting Policy for Single Population with Periodic Coefficients. Mathematical Bio-sciences, 152, 165-178. https://doi.org/10.1016/S0025-5564(98)10024-X