天津职业技术师范大学理学院，天津

收稿日期：2022年10月7日；录用日期：2022年11月1日；发布日期：2022年11月9日

摘要

计算单项式理想定义的簇的维数与计算任意簇的维数不同，可以简化为计算理想中最小公共变量集的元素个数。根据单项式理想的这一特性，本文给出一种算法并利用符号计算软件进行实现，从而可以自动计算单项式理想定义的簇的维数。

关键词

单项式理想，仿射簇，代数集，维数

Symbolic Implementation of Calculation Dimension of a Class of Affine Varieties

Qinghui Fu

School of Science, Tianjin University of Technology and Education, Tianjin

Received: Oct. 7^th, 2022; accepted: Nov. 1^st, 2022; published: Nov. 9^th, 2022

ABSTRACT

Calculating the dimension of varieties defined by a monomial ideal is different from calculating the dimension of any varieties, and can be reduced to finding the number of elements of the least common set of variables in the ideal. According to this characteristic of monomials, an algorithm is designed and a code is written by Maple to calculate the dimension of varieties defined by monomialideal.

Keywords:Monomialideal, Affinevarieties, Algebraic Set, Dimension

Copyright © 2022 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

簇的维数是代数几何中的一个基本概念，簇的一种刻画.但是计算一个簇的维数是比较困难的，其中计算由单项式理想定义的簇的维数是比较简单的。D. Cox等人在 [1] 中，总结了一种计算由单项式理想定义的簇的维数的方法。J. Herzog在 [2] 的第二部分中介绍了希尔伯特函数，可以用来计算簇的维数。K. Hulek在 [3] 中介绍了希尔伯特零点定理、克鲁尔维数的概念。这篇文章总结文献 [1] [2] [3] 中提到由单项式理想定义的簇的维数问题，并且介绍一种算法，用来计算由单项式理想定义的簇的维数。最后利用maple实现程序，并且通过实例论证整个过程是可以用计算机软件实现。

2. 基础知识

我们定义数域k上的n维仿射空间为：

$A^n:=\left\{\left(a_1,a_2,a_3,\cdots ,a_n\right)|\forall a_i\in k\right\}$.

定义1：设子集 $X\in A^n$，那么X生成的消失理想如下：

$I\left(X\right)=\left\{f\in k\left[x_1,x_2,\cdots ,x_n\right]|\forall P\in X,f\left(P\right)=0\right\}$.

可以证明上述定义的 $I\left(X\right)$ 为 $k\left[x_1,x_2,\cdots ,x_n\right]$ 中的一个理想。

定义2：设 $k\left[x_1,x_2,\cdots ,x_n\right]$ 是在数域k的n个元多项式环，对于环中的一个子集J，定义由J生成的簇(代数集)：

$V\left(J\right)=\left\{P\in A^n|\forall f\in J,f\left(P\right)=0\right\}$.

根据上面的定义以及希尔伯特零点定理 [3]，可以在 $k\left[x_1,x_2,\cdots ,x_n\right]$ 中的理想与 $A^n$ 中子集定义出一个映射。那么在这个映射下， $k\left[x_1,x_2,\cdots ,x_n\right]$ 中的素理想与 $A^n$ 不可约簇是一一对应的 [4]。

定理1：假设 $A=\langle f_1,f_2,\cdots ,f_s\rangle$ 和 $B=\langle g_1,g_2,\cdots ,g_t\rangle$ 是 $k\left[x_1,x_2,\cdots ,x_n\right]$ 中的理想， $V\left(A\right)$ 和 $V\left(B\right)$ 是 $A^n$ 中

的仿射簇，那么两个簇的交集和并集也是簇，并且

$V\left(A\right)\cup V\left(B\right)=V\left(f_1{g}_1|1\le i\le s,1\le j\le t\right)$,

$V\left(A\right)\cap V\left(B\right)=V\left(\langle f_1,f_2,\cdots ,f_s,g_1,g_2,\cdots ,g_t\rangle \right)$.

定理2：假设簇X非空，其对应的消去理想是 $I\left(X\right)$，那么X是不可约簇当且仅当 $I\left(X\right)$ 是素理想。

其中不可约簇是指不存在 $X=X_1\cup X_2$，其中 $X_1$，$X_2$ 是X的两个真子集， $I\left(X\right)$ 素理想是指，若 $a\cdot b\in I\left(X\right)$，那么必有 $a\in I\left(X\right)$ 或 $b\in I\left(X\right)$ 成立。

根据文献4定理3.9在 $k\left[x_1,x_2,\cdots ,x_n\right]$ 中素谱的诺特性质，和素理想和不可约簇的对应关系，可以证

明每个由不可约簇构成的降链具有有限长度。就像计算线性空间的维数一样。这里将降链的最大长度定义为簇的维数。

定义3：一个簇V的克鲁尔维数(krull)是V的最长降链的长度krdim $V=n$。其中降链是

$V=V_0⊋V_1⊋V_2⊋V_3⊋\cdots ⊋V_n\ne \varnothing$.

根据上述定义，计算簇的维数要找到一条最长不可约簇的降链。利用 $k\left[x_1,x_2,\cdots ,x_n\right]$ 中的素理想与 $A^n$ 中的不可约簇之间的对应关系，我们可以将上述问题转化为寻找最长素理想构成的降链的问题。

定义4：假设 $V\left(I\right)$ 是 $k\left[x_1,x_2,\cdots ,x_n\right]$ 中的一个单项式理想，那么 $I=\langle f_1,f_2,\cdots ,f_n\rangle$ 中的每一个生成元 $f_i$ $\left(i=1,2,\cdots ,n\right)$ 都是单项式。

由于计算一般簇的维数是比较困难的，下面本文考虑一类由单项式理想的定义的簇。

3. 单项式理想所定义的簇维数

由于单项式中的任意非零次数的变量取零时，单项式就会为零。所以单项式理想的簇我们只需要考虑由类似坐标超平面来构成的。如下例所示：

例1：假设在 $k\left[x_1,x_2,\cdots ,x_n\right]$ 中有一个单项式理想 $I=\langle x_2^2{x}_3^3,x_1^5{x}_3^4,x_1^2{x}_2{x}_3^2\rangle$，那么：

$\begin{array}{c}V\left(I\right)=V\left(\langle x_2^2{x}_3^3,x_1^5{x}_3^4,x_1^2{x}_2{x}_3^2\rangle \right)\\ =V\left(\langle x_2^2{x}_3^3\rangle \right)\cap V\left(\langle x_1^5{x}_3^4\rangle \right)\cap V\left(\langle x_1^2{x}_2{x}_3^2\rangle \right)\\ =V\left(\langle x_2{x}_3\rangle \right)\cap V\left(\langle x_1{x}_3\rangle \right)\cap V\left(\langle x_1{x}_2{x}_3\rangle \right)\\ =\left[V\left(\langle x_2\rangle \right)\cup V\left(\langle x_3\rangle \right)\right]\cap \left[V\left(\langle x_1\rangle \right)\cup V\left(\langle x_2\rangle \right)\right]\\ \cap \left[V\left(\langle x_1\rangle \right)\cup V\left(\langle x_2\rangle \right)\cup V\left(\langle x_3\rangle \right)\right]\end{array}$

簇 $V\left(\langle x_2\rangle \right)\cup V\left(\langle x_3\rangle \right)$，簇 $V\left(\langle x_1\rangle \right)\cup V\left(\langle x_1\rangle \right)$，簇 $V\left(\langle x_1\rangle \right)\cup V\left(\langle x_2\rangle \right)\cup V\left(\langle x_3\rangle \right)$ 如下图：

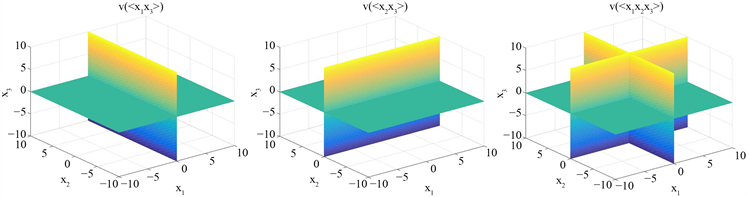
三个簇取交集不难看出是：

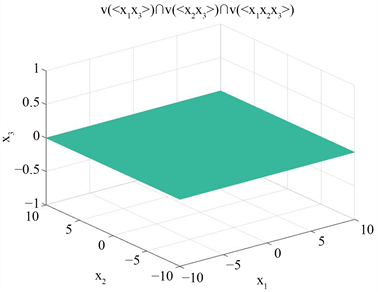
上面这个平面计算克鲁尔维数，先找到最长一条由不可约簇构成的链：

$V_2⊋V_1⊋V_0$.

$V_0$ 表示 $\left(0,0,0\right)$ 点， $V_1$ 表示 $\left(a,0,0\right)$ 其中 $a\in K$。$V_2$ 表示 $\left(a,b,0\right)$ 其中 $a,b\in K$，也就是上面的平面。在这个 $V\left(I\right)$ 中最长可以找到由三个不可约簇构成的降链。根据克鲁尔维数的定义可知：

$\text{krdim}\pi \left(V_2\right)=2$.

与之相对的素理想链：

$\langle x,y,z\rangle ⊋\langle x,y\rangle ⊋\langle x\rangle$.

受上例启发，可以将上述过程简化为计算理想中最小公共变量集的元素个数，一般的簇并不能做到这点。

定理3：设单项式理想 $I\in k\left[x_1,x_2,\cdots ,x_n\right]$，那么单项式理想的簇 $V\left(I\right)$ 的维数和理想I公共变量有下述关系：

$\text{krdim}\left(V\left(I\right)\right)=\text{krdim}\left(V\left(\langle x_{q1}\rangle \right)\cup V\left(\langle x_{q2}\rangle \right)\cup \cdots \cup V\left(\langle x_{qn}\rangle \right)\right)$,

其中 $x_{p1},x_{p2},\cdots ,x_{pq}$ 是在单项式理想I中出现的公共变量。

证明：设 $\left(m,n\in 0,1,2,\cdots \right)$，那么

$\begin{array}{l}V\left(\langle x_1^{\left(1,1\right)}{x}_2^{\left(1,2\right)}\cdots x_n^{\left(1,n\right)},x_1^{\left(2,1\right)}{x}_2^{\left(2,2\right)}\cdots x_n^{\left(2,n\right)},\cdots ,x_1^{\left(m,1\right)}{x}_2^{\left(m,2\right)}\cdots x_n^{\left(m,n\right)}\rangle \right)\\ =\underset{i=1}{\overset{m}{{\displaystyle \cap }}}V\left(\langle x_1^{\left(i,1\right)}{x}_2^{\left(i,2\right)}\cdots x_n^{\left(i,n\right)}\rangle \right)\\ =\underset{i=1}{\overset{m}{{\displaystyle \cap }}}\left[\underset{j=1}{\overset{n}{{\displaystyle \cup }}}V\left(\langle x_j^{i,j}\rangle \right)\right]\\ =V\left(\langle x_{p1}^{k1}\rangle \right)\cup V\left(\langle x_{p2}^{k2}\rangle \right)\cup \cdots \cup V\left(\langle x_{pn}^{ks}\rangle \right)\\ =V\left(\langle x_{p1}\rangle \right)\cup V\left(\langle x_{p1}\rangle \right)\cup \cdots \cup V\left(\langle x_{p1}\rangle \right),\end{array}$

其中 $x_{p1},x_{p2},\cdots ,x_{pq}$ 是在单项式理想I中出现的公共变量。

根据定理6，把例5改成寻找公共变量集，

$I=\langle x_2^2{x}_3^3,x_1^5{x}_3^4,x_1^2{x}_2{x}_3^2\rangle$.

公共变量集合为：

$\left\{\left\{x_1,x_2,x_3\right\},\left\{x_1,x_2\right\},\left\{x_1,x_3\right\},\left\{x_2,x_3\right\},\left\{x_3\right\}\right\}$,

其中最少的是 $\left\{x_3\right\}$，个数为1。那么该簇的维数就等于：

$\text{krdim}\left(V\left(I\right)\right)=3-1=2$.

4. 单项式理想簇的维数程序实现

根据上面的寻找最小公共变量集的做法，这里设计一种maple程序。先将全部的变元取出来，根据choose算法，做成公共变量集合，最后找到其中变元最少的。

用变量做成字符串，求全部子集。然后按照子集中元素的个数排列，将元素个数少的子集排在前面。choose算法如下：

下面是利用maple执行上述算法得出的结果。

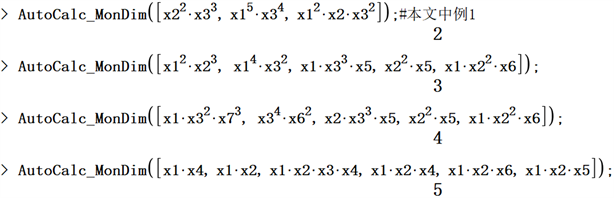
后面两个例子直接计算的话是比较复杂的。上面的几个例子可以看出到，利用maple执行上诉算法的程序，可以快捷有效的计算出一个由单项式定义的簇的维数。这里choose算法中对数据的处理会按照2ⁿ增加，本质上求理想中最少公共变量集的元素个数这一做法是不需要choose算法中全部的结果。如果可以精准的找到最少公共变量集，是可以对效率有很大的提升。

文章引用

富庆辉. 一类仿射簇的维数计算的程序实现
Symbolic Implementation of Calculation Dimension of a Class of Affine Varieties[J]. 应用数学进展, 2022, 11(11): 7653-7658. https://doi.org/10.12677/AAM.2022.1111810

参考文献