Pure Mathematics
Vol.08 No.03(2018), Article ID:25193,7
pages
10.12677/PM.2018.83041
The Rank of Eigenvalue of a Four-Order Ordinary Differential Operator under Coupled Boundary Condition
Tao Peng1, Yunlan Gao2*, Xiaojuan Qin2
1Zibo Construction Engineering School, Zibo Shandong
2School of Science, Inner Mongolia University of Technology, Hohhot Inner Mongolia
Received: May 10th, 2018; accepted: May 23rd, 2018; published: May 30th, 2018

ABSTRACT
In this paper, a class of four-order ordinary differential operators with coupled boundary conditions is discussed. By using the Lagrange equation of the operator's corresponding formula, the relation between the rank of the eigenvalue of the problem and the zero point weight of an entire function is obtained.
Keywords:Eigenvalue, Eigenfunction, Rank, Ordinary Differential Operators
某耦合边界条件下四阶常微分算子特征值的秩
彭涛1,高云兰2*,秦小娟2
1淄博建筑工程学校,山东 淄博
2内蒙古工业大学理学院,内蒙古 呼和浩特
收稿日期:2018年5月10日;录用日期:2018年5月23日;发布日期:2018年5月30日

摘 要
本文讨论了一类具有耦合边界条件的四阶常微分算子,利用该算子相应算式的拉格朗日等式,得到问题特征值的秩与某整函数的零点重数之间的联系。
关键词 :特征值,特征函数,秩,常微分算子

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 问题的提出
在微分算子的领域中,许多学者对特征值问题进行了研究,如文献 [1] - [7] ,这些文献的研究方法均为将特征值问题的讨论转化为一个整函数零点的讨论,本文研究了一类具有耦合边界条件的四阶微分算子,得到问题特征值的秩与某整函数的零点重数之间的联系。
记
,
,
。考虑以下耦合边界条件下的特征值问题:
(1)
(2)
设
是四个满足(1)式的解,它们分别在
处满足
,
,
显然,Wronsky行列式
,
是(1)的四个线性无关的解,且可以构成(1)的基础解系。
设
是问题(1) (2)的特征函数,其中
是特征值,则
满足(2)式,即:
(3)
方程组(3)的系数行列式为
,即:
(4)
方程组(3)可以看作是未知数
的方程组,由特征函数的定义知,此方程组存在非零解,故系数行列式
。类似于文献 [1] 中命题1,2的证明,我们可以得到如下两个命题。
命题1:记

显然,
。
是特征值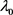 的秩,则以下两结论成立:
的秩,则以下两结论成立:
i)
为问题(1)(2)的特征值
。
ii)
。
命题2:设
是四个满足(1)式的解,记为
. (5)
记
,
,其中
。如果
且
,则:
i)
是问题(1)(2)的特征函数,则满足
ii)
的极大无关组个数为
。
引理1:算式
有以下的Lagrange恒等式
引理2:设
是(5)式所给出的特征函数。
是
的零点,则有:
其中
证明:利用引理1有
分别取
,即得结论。
引理3:设
是(5)式所给出的特征函数
,
是特征值。简记
,记一元函数
关于
求导后在 处的取值为
,记两个函数
,
的内积为
,其定义为
处的取值为
,记两个函数
,
的内积为
,其定义为
,
这样可以得到16个恒等式,写成矩阵形式如下:
证明:
其中
,接着利用洛必达法则,可得
当
分别取1,2,3,4时,就可以得到定理的结论。
2. 主要结果与证明
定理1:设
为问题(1) (2)的特征值,其秩记为
,则
1)
的充要条件是
且
。
2) 当满足条件
或
时,
的充要条件是

3) 当满足条件
和
时,
的充要条件是
4) 当满足条件
和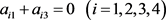 时,
时,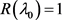 的充要条件是
的充要条件是
证明:(1)~(4)的充分性显然成立。下面证明必要性。
1)
,
对应4个线性无关的特征函数
,
。
因为
,且
,故
。
又因为求导后展开的每个行列式中至少有一行未被求导,从而行列式
。同理可得
。
对
关于
求四阶导数后,在
处只剩一项。
上式右端是Crame行列式,故由文献 [2] 知,
,故
。
2) 先证在
条件下的结论,另一种情况类似证明。
,可以生成3个线性无关的特征函数,不妨取为:
则右端
阶矩阵至少存在一个三阶子式非零,不妨取为:
此行列式展开的六项中至少有一项非零,为讨论方便取为
。
经过初等变换得
显然
,
,
。
经过等值变换得
当
时,
下面说明
,由以上假设知:
因此
是线性无关的。
另一方面,由引理2以及
知,
假设
,由上式可得到
因为系数行列式不等于零,故有
,
,即
也是特征函数,这与已知矛盾,故
。
(3) (4)仿照
的方法,进行证明。
基金项目
国家自然科学基金(11661059),内蒙古自然科学基金(2017MS(LH)0103)。
文章引用
彭 涛,高云兰,秦小娟. 某耦合边界条件下四阶常微分算子特征值的秩
The Rank of Eigenvalue of a Four-Order Ordinary Differential Operator under Coupled Boundary Condition[J]. 理论数学, 2018, 08(03): 308-314. https://doi.org/10.12677/PM.2018.83041
参考文献
- 1. 李梦如, 郑莹. 周期边界条件下四阶常微分算子特征值的秩[J]. 郑州大学学报(理学版), 2004, 36(4): 1-5.
- 2. 那汤松, 著. 实变函数论(上册) [M]. 徐瑞云, 译. 北京: 高等教育出版社, 1956.
- 3. 曹之江. 常微分算子[M]. 上海: 上海科学技术出版社, 1987.
- 4. 傅守忠, 王忠. Sturm-Liouville问题的m-函数与谱[J]. 应用数学学报, 2015, 38(2): 350-355.
- 5. 杨凤伟. 左定周期Sturm-Liouville问题的谱性质[J]. 黑龙江大学自然科学学报, 2012, 29(6): 764-766.
- 6. Kong, Q., Wu, H. and Zettl, A. (1999) Dependence of the nth Sturm-Liouville Eigenvalue on the Problems. Journal of Differential Equations, 156, 328-354. https://doi.org/10.1006/jdeq.1998.3613
- 7. Everitt, W.N., Wong, M.K.K. and Zettl, A. (1983) Oscillation of Eigenfunctions of Weighted Regular Sturm-Liouville Problems. Journal of the London Mathematical Society, 27, 106-120. https://doi.org/10.1112/jlms/s2-27.1.106






 的秩,则以下两结论成立:
的秩,则以下两结论成立: 处的取值为
,记两个函数
,
的内积为
,其定义为
处的取值为
,记两个函数
,
的内积为
,其定义为
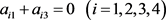 时,
时,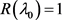 的充要条件是
的充要条件是