Pure Mathematics
Vol.08 No.04(2018), Article ID:26026,9
pages
10.12677/PM.2018.84060
A Class of Spectral Method for Solving Unsteady Navier-Stokes Equations
Jiansen Li, Jun Liu, Jiao Zhang, Xinyue Fan*
School of Mathematics and Statistics, Guizhou University, Guiyang Guizhou

Received: Jun. 30th, 2018; accepted: Jul. 15th, 2018; published: Jul. 23rd, 2018

ABSTRACT
This paper focuses on the issue about using numerical computation to solve unsteady Navier-Stokes equations. We present a scheme called nonlinear Galerkin-Legendre Spectral method, which combines the Legendre spectral method with nonlinear Galerkin-Legendre method. Therefore, it is not necessary to meet Babuska-Brezzi inequality condition in the velocity space and pressure space. In this paper, we give a spectral scheme of nonlinear Galerkin-Legendre methods for solving 2D N-S equations. What’s more, we also provide the error estimation and proof the stability of this scheme. The method based on the separate calculation of viscous flow and potential flow, was used to solve the problem of plane buffeting, and has been replaced by the method based on the incompressible N-S equations. Therefore, it is necessary to use the spectral method to study the chattering problem of aircraft and to reduce the resistance by error analysis and to save energy.
Keywords:Navier-Stokes Equation, Nonlinear Galerkin Method, Buffet Problem, Legendre Spectral Method, Error Estimation
基于Navier-Stokes方程分析飞机抖振问题
李建森,刘 俊,张 姣,范馨月*
贵州大学数学与统计学院,贵州 贵阳

收稿日期:2018年6月30日;录用日期:2018年7月15日;发布日期:2018年7月23日

摘 要
针对不定常的Navier-Stokes方程,给出了一种非线性Galerkin-Legendre谱方法(GL方法),该方法是将勒让德谱方法和非线性Gelerkin方法结合起来,使得速度与压力的混合元空间不需要满足离散的Babuška-Brezzi不等式条件,给出了GL方法的谱格式,并给出该方法的稳定性证明和误差估计。关于飞机抖振问题已经由基于不可压缩N-S方程的方法的研究取代了原来粘、位流分开计算的研究,因此用谱方法研究飞机抖振问题,通过误差分析,减少阻力,达到节约能源的目的。
关键词 :Navier-Stokes方程,非线性Galerkin法,抖振问题,Legendre谱方法,误差估计

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
飞机发生抖振的原因有很多。比如随着飞行迎角的增加,较强的逆压梯度引起飞机表面流动分离;飞机表面部分的非流线型外形(例如打开扰流片或减速板时)引起分离;跨音速飞行时,激波附面层干扰引起激波振荡和流动分离;一个部件处于另一个部件的尾流中;飞行器尾部的过度收缩引起分离等等。飞机抖振问题主要分为两类:抖振分为机翼抖振和垂尾抖振。一般情况下抖振是有害的。当飞机发生抖振时,会出现飞机上仰、机翼下坠、偏头、摇摆等现象,导致飞机的飞行品质变坏,除了使乘务员的工作效率下降、旅客感到不舒适外,还会引起机载设备工作环境恶化而不能正常工作。严重情况下,会出现机翼、垂尾折断等飞行事故;严重的抖振还可能导致驾驶员失去操纵能力,从而危及飞行及驾驶员的安全。所以,飞行器设计都把抖振作为一个重要的因素予以考虑,这就要求必须测出抖振产生的误差,通过预测出的误差结果,利用一些方法改进飞机机翼设计或者使用更好地材料;所以抖振响应的预测以及改进也显得很重要。N-S方程数值计算是利用数值方法研究抖振问题的基础。
非线性Galerkin方法是一种用在空间离散的分解方法,可以用来求解具有耗散项的偏微分方程的近似解的多重水平方法 [1]。该方法由Temam,Marion,Devulder,Titi在Fourier谱离散化时提出来的。Marion [2] 将非线性Galerkin方法应用于混合元法中,用来处理非定常的Navier-Stokes方程。罗振东 [3] 等又将非线性Galerkin混元法推广应用于非定常的热传导–对流问题的半离散和全离散格式,提出了定常Navier-Stokes非线性Glerkin混元法及其后验估计。
对于解定常的Navier-Stokes方程的混合有限元法,一个重要的约束条件就是必须满足Babuška-Brezzi不等式 [4]。为了摆脱这一局限,CBB方法随之产生,罗振东 [2] 将带有余量的最小二乘法和Galerkin方法结合起来应用于处理定常的Navier-Stokes方程,给出了N-S方程的解关于参数(H和h)的收敛性和稳定性。
研究的目的是将非线性Galerkin方法和Legendre谱方法结合起来(称为GL方法)处理定常的Navier-Stokes方程(飞机抖振数学模型),提出了该方程的GL格式,并且给出了误差估计 [5] ,最后数值算例验证了此结果的准确性,通过与变分法和有限元方法比较分析出,GL方法对改良飞机抖振问题有指导性作用。
2. 经典Galerkin方法下的结论
2.1. 预备知识
双线性 设 是一个双线性泛函 [6] ,则
三线性设 是一个三线性泛函,则
对于 有下列性质(参见 [7] ):
2.2. Galerkin方法的弱形式
设 是一个有界区域。考虑下面定常N-S方程 [8] :
问题I求 满足
(1)
其中u表示速度,p表示压力,f表示外力, 是雷诺数的倒数,是常数。
如下记号:
问题I的变分形式为:
问题I*求 满足
其中
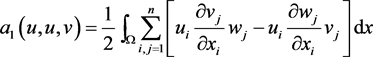 ,
,
.
设 和 分别是X和M空间中次数不超过N的多项式空间,则(1)的谱格式为:
(2)
从文献 [7] 可以得到以下结论。
定理1.1 如果Babuška不等式成立,那么
其中N为插值多项式的个数, 满足Babuška不等式。
3. 非线性Galerkin-Legendre谱方法
3.1. 准备知识
先引进一些记号。设
,
,
,
,
.
注意到
和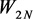 中的元素均在
处为零,即在边界上为零。
中的元素均在
处为零,即在边界上为零。
设 是 的正交投影算子,即
, ,
设 是 的投影算子,即
, ,
3.2. 非线性Galerkin-Legendre方法
问题I的非线性Galerkin-Lengedre格式为 [9]
问题I**求 ,和 ,使得
(3)
引理2.1根据三线性泛函的性质,有以下结论
以上引理在 [10] 中已经得证。
定理2.1 在引理2.1成立下,对充分大的N,我们有
,
其中C为与 有关的常数,K为与 有关的常数,M为与 有关的常数, ,N为插值多项式的个数。
证明:因为 的定义满足
记
, , .
显然 , , ,特别地
由(1)式与(3)相减
整理得到
不妨取 , ,于是
其中
注意到 。根据Young不等式
因为 ,应用Young不等式,Poincare不等式以及 ,对充分大的N,有
因为 ,
综上
.
由Gronwall不等式
其中 ,N为基函数个数。
现在对压力作误差估计。
记 在文献 [11] 中有以下结果:
引理2.2 如果Babuška条件成立,则
下面我们根据Babuška不等式性质以及速度误差的相关结论有
(1)式减去(3)式
由Babuška不等式,找任意 , 则
注意到 , 。
因此
根据 ,考虑到 与 正交,文献 [5] 有以下结论
,
因此
综上结论,我们有如下误差估计
其中C是与 有关的常数,K是与 有关的常数,M是与 有关的常数, 。
4. 数值算例
我们考虑如下的N-S方程(飞机抖振数学模型):
(4)
其中 , ,速度空间是一个狄利克雷边界,时间上使用差分法(显示欧拉格式),压强空间上用次数不超过N的多项式空间近似逼近,得到如下格式:
(5)
现对u做Legendre多项式插值,即
,
对p做Legendre多项式插值,即
、 是插值系数, 是插值基函数。
将这些近似多项式和代入上述(5),则有
这是一个线性方程组形式,算法的步骤如下:
已知方程(4) 的精确解
处理不可压缩N-S方程的谱方法与传统的变分法以及有限元法处理N-S方程的区别很明显,从表1和表2可以看出相同的时间间隔,谱方法得出来的结果比经典格式的结果更加精确;表3中的误差表
Table 1. The comparison of error estimates for velocity in two different formats with N = 16 and T = 1
表1. N = 16和T = 1两种不同格式下的速度的误差估计的比较
Table 2. The comparison of error estimates for pressure in two different formats with N = 16 and T = 1
表2. N = 16和T = 1两种不同格式下的压强的误差估计的比较
Table 3. The error estimates and convergence order for different time intervals and N with T = 1 and T = 2
表3. T = 1和T = 2时不同时间间隔和不同N的误差估计以及收敛阶
示在T = 1、T = 2时刻下的速度误差和压力误差总和,从表3中可以看出不同时间间隔下,时间间隔对方程的误差估计影响更大,该方程的收敛阶可以用 来刻画,并且速度收敛阶是1;在相同时间间隔和不同N下,N对方程的误差估计影响更大,该方程的收敛阶可以用N来刻画,且随着基函数的个数N的增加,误差越来越少,所得的精度越高,收敛结果也符合谱方法的收敛阶,以N的负指数次幂速度收敛精确解。
5. 结语
研究提出了一类求解定常纳维斯托克斯方程的谱方法,基于二维不可压缩N-S方程给出了LG格式,并且得出相关误差结果,比较了该方法与经典方法和有限元方法的区别,从数值结果我们可以发现LG谱方法下速度逼近的收敛率是最优的,而压强逼近的收敛率也很好。从表格上可以看出当解 是光滑的,即使对较小的N也能得到很好的结果,而且计算量不大,这充分体现了LG谱方法的优越性。基于N-S方程的GL方法的数值分析,可以看出对于飞机抖振问题,可以通过减少与空气阻力,达到节约能源的目的。
基金项目
贵州省科学技术基金项目(黔科合J字[2013]2128),贵州省大数据重点实验室开放课题 (2017BDKFJJ012)。
文章引用
李建森,刘 俊,张 姣,范馨月. 基于Navier-Stokes方程分析飞机抖振问题
A Class of Spectral Method for Solving Unsteady Navier-Stokes Equations[J]. 理论数学, 2018, 08(04): 450-458. https://doi.org/10.12677/PM.2018.84060
参考文献
- 1. Temam, R. (2013) Navier-Stokes Equations, Theory and Numerical Analysis. AMS Chelsea Edition, American Mathematical Society, Rhode Island.
- 2. Marion, M. and Temam, R. (1989) Nonlinear Galerkin Methods. SIAM Journal on Numerical Analysis, 2, 1139-1157. https://doi.org/10.1137/0726063
- 3. 罗振东, 朱江, 王会军, 等. 定常的Navier-Stokes方程的非线性Galerkin/Petrov最小二乘混元法[J]. 应用数学和力学, 2011, 7(7): 697-887.
- 4. Shen, J. and Wang, L.-L. (2011) Spectral Methods, Springer, Heideberg, Dordrecht, London, New York.
- 5. 何银年, 黄艾香. 非定常N-S方程的非线性Galerkin算法及其误差估计[J]. 系统科学与数学, 1991, 19(1): 116-122.
- 6. 向新民. 谱方法的数值分析[M]. 北京: 科学出版社, 2000: 153-156.
- 7. France, L.P. and Hughes, T.J. (1998) Two Classes of Mixed Finite Element Methods. Computer Methods in Applied Mechanics and Engineering, 69, 89-129. https://doi.org/10.1016/0045-7825(88)90168-5
- 8. 牟让科, 杨永年. 飞机抖振问题研究进展[J]. 应用力学学报, 2001, 18(s1): 143-149.
- 9. Shen, J. and Yu, H. (2010) Efficient Spectral Sparse Grid Methods and Applications to High Dimensional Elliptic Problems. SIAM Journal on Scientific Computing, 32, 3228-3250. https://doi.org/10.1137/100787842
- 10. 胡园园, 谢江, 张武, 等. 二维不可压缩Navier-Stokes方程的并行谱有限元法求解[J]. 计算机应用, 2017(1): 42-47
- 11. Liu, J. and Fan, X.Y. (2017) Legendre-Galerkin Methods for Nonlinear Partial Differential Equations. Advance in Intelligent Systems Research, 23, 1951-6851. https://doi.org/10.2991/icmia-17.2017.71
NOTES
*通讯作者。
