Pure Mathematics
Vol.
09
No.
03
(
2019
), Article ID:
30321
,
8
pages
10.12677/PM.2019.93048
Uniqueness of Entire Functions That Share Small Function with Their Difference Polynomials
Xiaohuang Huang, Dan Liu
Institute of Applied Mathematics, South China Agricultural University, Guangzhou Guangdong
Received: Apr. 26th, 2019; accepted: May 6th, 2019; published: May 21st, 2019

ABSTRACT
In this paper, we study the uniqueness of difference operators about transcendental entire function with a Borel entire exceptional function, which shares a small function with its difference polynomial. Furthermore, under the above assumption, we replace the condition “Borel entire exceptional function” by “ ”,and get the same result when shares CM with its difference polynomial.
Keywords:Entire Function, Shared Small Function, Difference Polynomials

整函数与其差分多项式的唯一性
黄小皇,刘丹
华南农业大学应用数学研究所,广东 广州
收稿日期:2019年4月26日;录用日期:2019年5月6日;发布日期:2019年5月21日

摘 要
本文研究关于涉及有穷级超越整函数
在有一个Borel整例外函数的条件下,
与其差分多项式
IM分担一个小函数
的唯一性问题。进一步在上述前提下,把条件“Borel整例外函数”改为“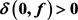 ”,且
与其差分多项式
IM分担一个小函数
,我们同样得到了相关的结果。
”,且
与其差分多项式
IM分担一个小函数
,我们同样得到了相关的结果。
关键词 :整函数,分担小函数,差分多项式

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在本文中,假设读者熟知Nevanlinna值分布理论的相关基础知识以及常见符号 [1] [2] 。设
是复平面上的亚纯函数,a∈C 为任意的复数,定义a关于f的亏量为
,当
时,a称为f的Nevanlinna亏值。定义
与
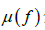 分别为
的级与下级。设a为开平面内的亚纯函数,如果
,则称a为f小函数。设f与g均为非常数亚纯函数,a为f与g的公共小函数,如果
与
的零点相同且每个零点重级也相同,则称f与g CM分担a。如果
与
的零点相同,不考虑零点重级,则称f与g IM分担a。
分别为
的级与下级。设a为开平面内的亚纯函数,如果
,则称a为f小函数。设f与g均为非常数亚纯函数,a为f与g的公共小函数,如果
与
的零点相同且每个零点重级也相同,则称f与g CM分担a。如果
与
的零点相同,不考虑零点重级,则称f与g IM分担a。
设k为正整数。记
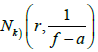 为
的重级
的零点密指量,且计重数。
为
的重级
的零点密指量且计重数。记
为
的零点精简密指量,且不计重数。
为
的零点精简密指量,且不计重数。
为
的重级
的零点密指量,且计重数。
为
的重级
的零点密指量且计重数。记
为
的零点精简密指量,且不计重数。
为
的零点精简密指量,且不计重数。
设F与G均为非常数亚纯函数,且F与G IM分担1。设
为F的一个重级为p的1值点,同时为G的一个重级为q的1值点。记
为F的那些重级
的1值点;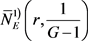 为F的那些重级
的1值点;记
为F的那些重级
的1值点。以上所定义的计数函数每一点只计一次。同样可以定义
,
,
。若F与G IM分担1,则
为F的那些重级
的1值点;记
为F的那些重级
的1值点。以上所定义的计数函数每一点只计一次。同样可以定义
,
,
。若F与G IM分担1,则
设f为非常数有穷正级为
的亚纯函数,
为f的一个小函数。若
,则称
为f的一个Borel例外函数。当 时,定义
的零点个数为有穷个。
时,定义
的零点个数为有穷个。
另外,我们需要定义一些差分算子的符号。设f为非常数亚纯函数, 为f的小函数, 为判别的有穷复数。令
为f的差分多项式。最近,许多人做了关于复差分唯一性的问题。2018年,Huang-Zhang [3] 证明了:
定理A 设 为开平面上的有穷级的超越整函数, 为f的一个Borel例外值, c∈C 为非零有穷复数。设 为 的一个小函数,若 与 CM分担 ,则 。
定理B 设 开平面有穷级的超越整函数, 为有穷复数。设 为 的一个小函数,若 与 CM分担 且 ,则 。
定理C 设 为开平面有穷级的超越整函数, 为有穷复数。设 为 的一个小函数。若 与 CM分担 且 ,则 。
本文推广并改进上述结果,证明了:
定理1 设 为开平面有穷级的超越整函数, 为f的一个Borel例外整函数,
为f的差分多项式,其中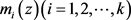 为f的整小函数,
为f的整小函数,
 k个判别的有穷复数。
k个判别的有穷复数。
又设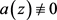 为
的一个整小函数,若
与
IM分担
,则
。
为
的一个整小函数,若
与
IM分担
,则
。
定理2 设 为开平面有穷级的超越整函数,
为f的差分多项式,其中
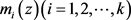 为f的整小函数
,
为f的整小函数
,
 为任意有穷复数。又
设
为
与
的一个公共小函数,若
与
CM分担
为任意有穷复数。又
设
为
与
的一个公共小函数,若
与
CM分担 且
且
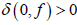 ,则
。
,则
。
2. 几个引理
引理1 [4] [5] [6] 设f为非常数有穷级亚纯函数, c∈C 为非零有穷复数。则
,
其中 ,除去r的一个集合E,且集合E的对数测度为有穷的。
引理2 [1] [2] 设f为非常数亚纯函数,则
.
引理3 [7] 设 ,其中F与G为两个非常数亚纯函数。若F与G IM分担1且 ,则
.
引理4 [2] 设f与g均为非常数亚纯函数, 分别为f与g的级。则
.
引理5 [2] 设f与g均为非常数亚纯函数,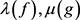 分别为f的级与g的下级。若
,则
分别为f的级与g的下级。若
,则
.
引理6 设f为非常数有穷级整函数。若 为f的一个Borel例外整函数,则 。
证 我们分为以下两种情形讨论:
情形1
。设
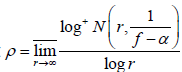 。因
。因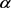 为f的一个Borel例外整函数且f为有穷级整函数,则有
。设
为f的一个Borel例外整函数且f为有穷级整函数,则有
。设
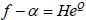 ,其中H为
的零点构成的典范乘积,以及Q为一非零多项式。由
,其中H为
的零点构成的典范乘积,以及Q为一非零多项式。由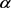 为f的整小函数,从而有
为f的整小函数,从而有
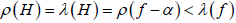 。显然有
,这可推出
。由引理4以及
为正规增长函数,我们可以得到
。显然有
,这可推出
。由引理4以及
为正规增长函数,我们可以得到
,
以及
,
即
。又由引理5可得
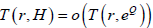 。因此
。因此
,
反过来也可得到 。这可推出 。故我们有
.
情形2
。由我们引言中所定义的
时
的零点个数为有穷个,直接可得
,于是有
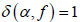 。证毕。
。证毕。
3. 定理1的证明
设
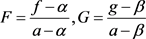 , (1)
, (1)
其中 。因为f与g IM分担a,a为整小函数。所以F与G IM分担1。由(1)有 。因为 为f的整Borel例外函数,则由引理6可以得到 。由引理1可以得到
,
即 。故 。从而有 与 。
定义H为引理3中的函数。假设 ,由引理3有
, (2)
其中 为 的零点计数函数,而不是F与 的零点计数函数。同样 也可类似定义。由Nevanlinna第二基本定理可得
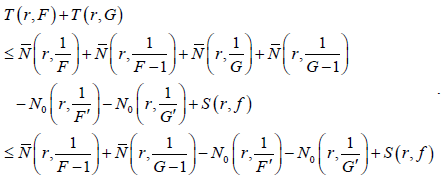 . (3)
. (3)
因为F与G IM分担1,所以我们有
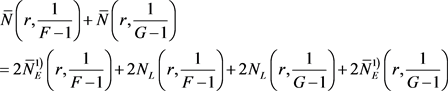 . (4)
. (4)
结合(2)与引理3可得
. (5)
容易发现
. (6)
由(5)与(6)得
. (7)
把(7)代入(3)可以得到
. (8)
由引理2又有
. (9)
由(8)与(9)可得
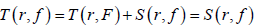 。矛盾。
。矛盾。
因此 。由引理3以及两边积分可得到
, (10)
其中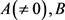 为常数。从(10)式又可以得到
为常数。从(10)式又可以得到
. (11)
我们分为以下三种情况讨论。
情形1 。由(11)可以得 。由Nevanlinna第二基本定理有
, (12)
即 。矛盾。
情形2 B = 0 。由(11)有
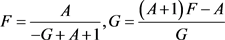 . (13)
. (13)
若 ,从(13)可得 。类似于情形1的证明过程我们同样可得矛盾。因此 A=1 。由(10)可知 ,即 。
情形3 。由(11)有
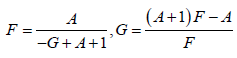 . (14)
. (14)
若 ,从(14)可得 ,即
. (15)
由(15)得到
. (16)
即 。矛盾。因此定理1得证。
4. 定理2的证明
假设 。因为f与g CM分担a,则
, (17)
其中H为非零多项式。从(17)可得
,
即 . (18)
根据上式可得到
,
即
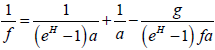 。
。
因此有
. (19)
另一方面,由Nevanlinna第二基本定理
,
于是有 。
因此我们有 。结合(19)立刻有 ,即 ,这与 矛盾。因此 ,其中C为非零常数。若 ,则有 ,这与设矛盾。故 ,从(17)得 。把上式代入(18),且由(19)可得 。即 ,这与 矛盾。因此 。定理2得证。
基金项目
国家自然科学基金(NO.11701188)资助。
文章引用
黄小皇,刘 丹. 整函数与其差分多项式的唯一性
Uniqueness of Entire Functions That Share Small Function with Their Difference Polynomials[J]. 理论数学, 2019, 09(03): 362-369. https://doi.org/10.12677/PM.2019.93048
参考文献
- 1. Yang, L. (1993) Value Distribution Theory. Springer-Verlag, Berlin
- 2. Yang, C.C. and Yi, H.X. (2003) Uniqueness Theory of Meromorphic Functions. Kluwer Academic Publishers Group, Dordrecht.
- 3. Huang, Z.B. and Zhang, R.R. (2018) Uniqueness of the Difference of Meromorphic Functions. Analysis Mathematica, 44, 461-473.
- 4. Heittokangas, Korhonen, R., Laine, I. and Rieppo, J. (2011) Uniqueness of Meromorphic Functions Sharing Values with Their Shifts. Complex Variables and Elliptic Equations, 56, 81-92.
https://doi.org/10.1080/17476930903394770 - 5. Halburd, R.G. and Korhonen, R.J. (2006) Nevanlinna Theory for the Difference Operator. Annales Academiæ Scientiarum Fennicæ Mathematica, 31, 463-478.
- 6. Chiang, Y.M. and Feng, S.J. (2008) On the Nevanlinna Characteristic of f (z + η) and Difference Equations in the Complex Plane. The Ramanujan Journal, 16, 105-129.
https://doi.org/10.1007/s11139-007-9101-1 - 7. Yi, H.X. (1997) Uniqueness Theorems for Meromorphic Functions Whose n-th Derivatives Share the Same 1-Points. Complex Variables, Theory and Application, 34, 421-436.
https://doi.org/10.1080/17476939708815064