Pure Mathematics
Vol.
11
No.
05
(
2021
), Article ID:
42628
,
14
pages
10.12677/PM.2021.115102
鲁洛克斯三角形上的Schwarz边值问题
郝延帅,刘华
天津职业技术师范大学理学院,天津

收稿日期:2021年4月17日;录用日期:2021年5月19日;发布日期:2021年5月26日

摘要
本文给出了鲁洛克斯三角形上一类特殊函数——其实部在边界上是循环对称函数——的Schwarz边值问题的解法,首先根据这类函数的特殊性将原问题进行改造,使其分别转化为实部在边界上关于实轴对称的Schwarz边值问题和实部在边界上关于实轴反对称的Schwarz边值问题,我们发现改造后的两个问题解之和就是原问题的解,然后通过对称扩张将改造后的两个问题转换为两组Riemann边值问题,最后通过求解这两组Riemann边值问题得到原问题的解。
关键词
Schwarz边值问题,鲁洛克斯三角形,Riemann-Hilbert边值问题
Schwarz Boundary Value Problem on Reuleaux Triangle
Yanshuai Hao, Hua Liu
School of Science, Tianjin University of Technology and Education, Tianjin

Received: Apr. 17th, 2021; accepted: May 19th, 2021; published: May 26th, 2021

ABSTRACT
This paper presents the approach to the Schwarz boundary value problem of a special function on the Reuleaux triangle, the real part of this function is a cyclosymmetric function on the boundary. According to the particularity of this type of function, the original problem is first transformed into a Schwarz boundary value problem with the real part symmetric about the real axis on the boundary and the real part antisymmetric Schwarz boundary value problem with the real axis on the boundary. The sum of the solutions of these two problems is equal to the solution of the original problem. After that, the two problems after the conversion are further converted into two sets of Riemann boundary value problems through the symmetric expansion, finally, the solution of the original problem is obtained by solving the solutions of the two sets of Riemann boundary value problems.
Keywords:Schwarz Boundary Value Problem, Reuleaux Triangle, Riemann-Hilbert Boundary Value Problem

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
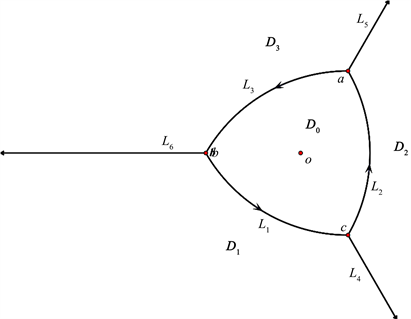
记
,其边界
,如图1所示。其中
,
图1. 鲁洛克斯三角形
定义1 [1]:设
定义于(开口或封闭的)光滑曲线
上,若对
上任意两点
,恒有
其中
都是确定的常数,则称
在
上满足
阶的Hölder条件或
条件,记为
或简记为
,而
称为Hölder指数,若不强调指出指数
,也可简记为
。
定义2 [1] [2]:设
是在射线
上的连续复函数。如果:
1) 在任意有限闭区间
上
2) 在
的邻域
内满足条件
则称
,或简记为
。若不强调
,可记为
。
注 [2]:若
且
,我们记为
或简记为
。
2. 提出问题
求在
内的全纯函数
,连续到
上,满足边值条件
(1)
其中
是已给在L上
的实函数。为简单起见,我们假设
3. 问题转化
令
代入(1)式,得到
(2)
(3)
由上述定义可知,
关于实轴对称,
关于实轴反对称,即
再由
可知
同理可知,
定义3:若
与
满足
则称
与
关于
互为对称点。
我们令 [3] [4] [5]
则,
与
关于
互为对称点,
与
关于
互为对称点,
与
关于
互为对称点。
由 [1] 可知,通过构造对称扩张可以将Schwarz边值问题等价转化为Riemann边值问题。下面我们给出
在外域
中的对称扩张,如下
记
易证,
是一分区全纯函数。
类似的,我们给出
在外域
中的对称扩张,如下
记
易证,
是一分区全纯函数。

Figure 2. Positive boundary value and its equivalent relation
图2. 正边值及其等价关系
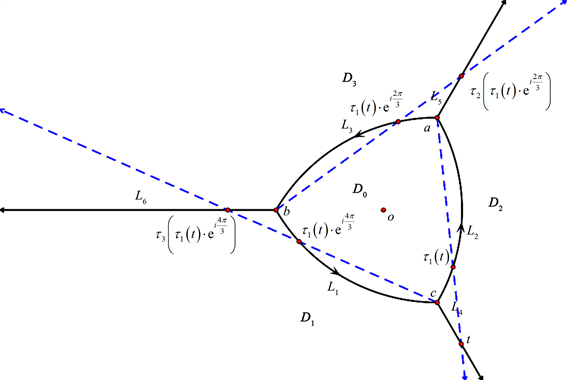
Figure 3. Negative boundary value and its equivalent relation
图3. 负边值及其等价关系
如图2和图3所示,通过计算可以得到如下性质:
其中
。如图4所示,有
可得
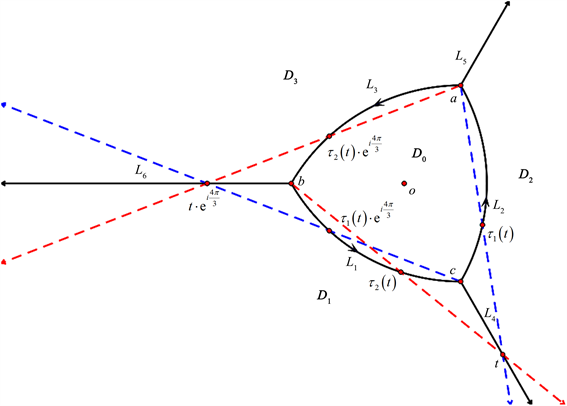
Figure 4. The boundary value problem on L4
图4. L4上的边值问题
同理,如图5所示,有
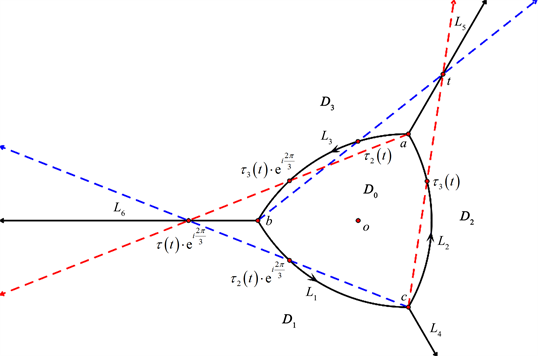
Figure 5. The boundary value problem on L5
图5. L5上的边值问题
可得
这就意味着,所求函数
在
上正负边值的实部相等,接下来我们将讨论其虚部之间的关系。
设
我们有
由C-R方程可得
记
是
关于
的对称点,有
其中
是
到
的直线段,
是
到
的直线段。从而,有
同理,我们有
问题(2)在满足条件
(4)
时,可等价转化为
(5)
由
可得
同理,由
可得
设
我们有
由C-R方程可得
记
是
关于
的对称点,有
其中
是
到
的直线段,
是
到
的直线段。我们假设
,从而有
同理,我们有
问题(3)在满足条件
(6)
时,可等价转化为
(7)
4. 求解问题
首先考虑开口弧段
上的边值问题,由于
,我们取
。引入函数
由 [1] 可知,在端点附近有
其中
分别在
附近沿
剖开的邻域
中全纯。
令
有
其中
分别在
中全纯。
我们假设在
类中求解,可知
,典则函数为
易得
在端点
附近是
阶的极点。
同理可知,
在
的端点
附近是
阶的极点,
在
的端点
附近是
阶的极点。从而,由对称扩张的性质可以推出
在
处是
阶的极点。
记
,给出函数
这里引用 [1] 中幂函数正负边值的定义
方程组(5)两边同时除以
,得
其中
由于
故
从而上述方程组的解为
为了满足条件(4),需构造
[1],我们令
其中
,
那么
是问题(2)的解,且满足条件(4)。
接下来,我们来求解方程组(7),令
易得
方程组(7)两边同时除以
,得
因为
所以,有
又
故解为
同样的,为了满足条件(6),下面需构造
,通过计算可得
其中
,那么
是问题(3)的解,且满足条件(6)。
5. 结论
最后,我们将问题(2)与问题(3)的解相加就得到了问题(1)的解,即
致谢
感谢在论文撰写期间对我提供指导和帮助的老师,感谢各位审稿专家的辛勤工作和指导。
文章引用
郝延帅,刘 华. 鲁洛克斯三角形上的Schwarz边值问题
Schwarz Boundary Value Problem on Reuleaux Triangle[J]. 理论数学, 2021, 11(05): 889-902. https://doi.org/10.12677/PM.2021.115102
参考文献
- 1. 路见可. 解析函数边值问题[M]. 武汉: 武汉大学出版社, 2004.
- 2. 王莹, 段萍, 杜金元. 正实轴上的Riemann边值问题[J]. 中国科学: 数学, 2017, 47(8): 887-918.
- 3. Begehr, H. (2014) Green Function for a Hyperbolic Strip and a Class of Related Plane Domains. Applicable Analysis, 93, 2370-2385. https://doi.org/10.1080/00036811.2014.926336
- 4. Begehr, H., Burgumbayeva, S. and Shupeyeva, B. (2018) Harmonic Green Functions for a Plane Domain with Two Touching Circles as Boundary. Advanced Mathematical Models and Applications, 3, 18-29.
- 5. Begehr, H., Burgumbayeva, S., Dauletkulova, A. and Lin, H.X. (2020) Har-monic Green Functions for the Almaty Apple. Complex Variables and Elliptic Equations, 65, 1814-1825. https://doi.org/10.1080/17476933.2019.1681413