Statistics and Application
Vol.
08
No.
02
(
2019
), Article ID:
29913
,
6
pages
10.12677/SA.2019.82040
VaR Research Based on Quantile Regression Model
—Taking Guizhou Bailing Stock as an Example
Shitong Fu, Liangqiong Jin
Institute of Data Science and Information Engineering, Guizhou Minzu University, Guiyang Guizhou

Received: Apr. 4th, 2019; accepted: Apr. 19th, 2019; published: Apr. 26th, 2019

ABSTRACT
Taking Guizhou Bailing as the research object, this paper established the VaR model of Quantile Regression to describe the risk measurement of stock data. The Quantile Regression model and the traditional GARCH model were compared with the risk measurement results of VaR. The empirical results show that the Quantile Regression method achieves relatively optimistic results in the data samples, and the accuracy of the results based on the Quantile Regression model is higher than that of the traditional model.
Keywords:Value-at-Risk, Quantile Regression Method, Garch Model
基于 分位数回归模型的VaR研究
——以贵州百灵股票为例
扶仕彤,金良琼
贵州民族大学,数据科学与信息工程学院,贵州 贵阳

收稿日期:2019年4月4日;录用日期:2019年4月19日;发布日期:2019年4月26日

摘 要
本文以贵州百灵股票作为研究对象,通过建立分位数回归的VaR模型,进行描述股票数据的风险测度研究。将分位数回归模型和传统GARCH模型对VaR的风险测度结果进行比较。实证结果表明,分位数回归方法在所取数据样本内取得了较为乐观的结果,基于分位数回归模型所得结果的精度要比传统模型要高。
关键词 :VaR风险测度,分位数回归方法,GARCH模型

Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
风险价值模型也称为VaR (Value at Risk),它具有金融市场风险测量的功能。金融市场的风险测量有很多不同的方法,其中,也逐渐广泛地出现了VaR的身影。一般情况下,金融时间序列通常并不符合正态分布,而基于统计学的观点,认为VaR实质是损失分布的一个分位数。因此这也是我们把VaR与分位数回归联想到一起的主要因素之一,其存在着一定的理论可行性。目前我国正处于金融市场的逐步发展阶段,国内不少学者也针对分位数回归模型对VaR风险测度方向上做了许多相关研究。张晨 [1] 等人在讲述我国金融风险管理的研究应用中,提及并且运用到了VaR模型。而像关静、史道济 [2] 不仅将分位数回归方法用于上证综指的风险测度上,并且文中还提出“外推法”的数据处理方法对比较极端情况下的分位数的VaR风险测度进行预测,结果可观。
分位数回归不再局限于统计领域而是被推广到经济领域上,第一次是由Konenker R. [3] 等研究者在1978年的文章中提及。分位数回归应用广泛,不仅是统计学领域上的一大重要工具,它在计量经济学的研究方向上也逐渐应用甚广。我们可以将其基本思想概括为响应变量通过解释变量的多个分位数以获得条件分布的对应方程。由于分位数回归方法能周到地表示出分布函数的局部信息,所以它相较于普通的回归方法有着更明显的优势。这也是金融数据的某些处理及研究可以从分位数回归模型入手理论思想的可行之处。VaR可以使用分位数回归模型来估计,实则是与分位数本身所具有的特征相关。而许启发 [4] 等人则将非参估计的神经网络方法与分位数回归方法结合在一起,对上证综指的VaR估计作了另一番的研究。
广义自回归条件异方差模型的一个特点在于对误差的方差也进行了建模,这是其与普通回归模型的不同之处。尤其适用在波动性的分析及预测上。这也是GARCH模型也被广泛运用到VaR研究中的原由之一。在互联网如此发达的如今,李治章和王帅 [5] 在2018年发表的文章中就提出了一个关于偏t分布的GARCH模型,并将其在互联网金融对各类商行的风险溢出效应的VaR研究上实现了,有着一定的指导意义。
本文以贵州百灵股票数据作为基础,主要给出基于分位数回归的VaR测度模型(模型一),将模型一和传统的GARCH模型进行对比分析,所得结果显示不论在稳健性方面还是精确度上,分位数回归模型均好于传统GARCH模型。
2. 基于分位数回归模型的VaR风险测度
设 为一元随机变量,其右连续分布函数 ; ,得到 的第 位分位数表示为:
(1)
是 维回归变量,当 时,定义 的条件分布为:
(2)
上式中, 是分位点,回归系数向量是 ,分位数回归系数向量 的取值与均值回归的不同点在于 的取值是随着分位点 的变化而变化的。我们通过(1.3)式的求解可以得到系数向量 的估计量 :
(3)
其中
(4)
金融时间序列为 时,假设 为金融资产收益, 为影响 的解释变量。则 的第 分位数表示为:
(5)
即是:
(6)
由VaR的性质即可得到基于分位数回归模型的VaR风险测度结果为:
(7)
通过设方程解释变量为滞后收益率可建立如下模型:
(8)
其中 为收益率; 为收益率 在 时刻的条件分位数,即是VaR; 为待估参数。当估计出上述模型的参数值后,即可得到不同置信水平下的对数收益率的VaR值。
3. 基于GARCH模型的VaR风险测度
一般地,GARCH模型可以表示为:
(9)
其中 为零均值、单位方差的独立同分布随机扰动序列。GARCH模型可以揭示金融市场的“波动聚集”特征和金融数据中的“后尾”现象。考虑一个GARCH(1, 1)模型的波动方程:
(10)
其中, 保证条件方差的正定性; 。若 易知模型的 无条件峰度将满足:
(11)
由(1)可知,若某金融资产的对数收益率 的一般时间序列模型可表示为:
(12)
(13)
由(4),(5)可得对数日收益率 的条件均值及方差向前一步预测,即得:
(14)
(15)
若假定 服从自由度为s的标准student -分布,则可得出持有期为1日的VaR为:
(16)
4. 实证研究
本文选取贵州百灵股票从2016年1月4日开始至2018年12月31日的时间区间共732个日收盘价格为研究对象。数据均来自锐思数据库,采取 计算对数形式收益率,其中 为各指数的每日收盘价, 为前一日收盘价。本文计算使用R.3.5.2软件进行编程。
4.1. 分位数回归的VaR模型
分位数回归本身的半参数性质使得无需假设参数的分布,故可直接建立分位数回归的VaR模型。首先我们将贵州百灵的收盘价的日对数收益率作为分位数回归的相应变量,设其滞后3期的收益率作为解释变量,在95%的置信水平下,通过R语言编程所得如下模型一:
(17)
通过上述模型,我们可以求得基于分位数回归模型在持有期内的VaR序列。例如2018年12月31日一天内的VaR值为155.88203万元,即表示贵州百灵公司在置信度95%的VaR值为150.88203万元。根据VaR的定义,其含义是指,该公司能够以95%的可能性保证,在2018年12月31日这一天内每一特定时点上的投资收益在未来24小时内,由于市场价格变动而带来的损失不会超过155.88203万元。
分别取 ,得到如图1的分位数回归估计结果。实线表示线性均值回归的估计结果,长、短虚线分别表示线性中位数回归估计结果( )以及剩余分位数取值时的回归估计结果。
根据定义,分位数回归的VaR模型可以简便的找到与置信度相对应的分位数,也就可以得到不同置信水平下的VaR值。并且,分位数 的取值足够小时,能够看出分位数回归模型对极端值的拟合更好。说明分位数回归模型对于边界数据的信息也能够描述。
4.2. GARCH的VaR模型
首先我们原始数据进行基本统计性质进行检验并做出序列的时序图(见图2),结果表明贵州百灵收益拒绝了正态分布的原假设,检验结果见表1。

Figure 1. Quantile regression model
图1. 分位数回归模型
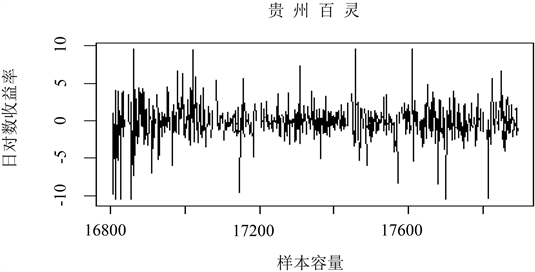
Figure 2. Time series diagram
图2. 时间序列图
Table 1. The result of the basic characteristic of logarithmic rate of return
表1. 对数收益率的基本特性结果表
从表1的检验结果中,偏度值为−11.57492,呈现出负偏性;峰度为9.28574,大于正态分布的峰度临界值3。因此,该收益率序列存在尖峰、后尾的特征。J-B统计量的P值远远小于0.05,从而得知序列拒绝了正态分布再通过LM统计量的P值接近于0则表明了序列有ARCH效应的情况存在。
由以上对原数据进行简单分析后,分布故考虑随机误差项服从student -分布,采用GARCH(1, 1)模型,通过R语言编程实现基于GARCH的VaR模型所得结果如下:
(18)
通过Kupiec似然比检验方 [6] 对模型一和GARCH模型作对比分析。由R软件得知其接受域大致在 。在置信度为95%的条件下,模型一下的VaR失败率约为4.74%,而GARCH模型中的VaR失败率为6.89%。两者对比之后,分位数回归模型的失败率要更接近5%,即GARCH模型低估了市场风险。因此分位数回归模型更优于传统的GARCH模型。分位数回归模型还可以更加简便的得到不同置信水平下的VaR值。并且通过取不同 的取值最后能够把整体数据的全面信息都反映出来。综上所述,模型一是可以较好地适应VaR风险测度的。
5. 总结
VaR已然成为当今国际上最为主流的一种有效的金融风险度量的工具,被金融各界人士广泛运用。文章基于分位数回归模型,对贵州百灵股票的VaR进行测度研究,通过Kupiec似然比检验将模型一与GARCH模型作了对比,得出GARCH模型失败率要高于模型一,故分位数回归模型在对VaR的风险测度研究上要比GARCH模型略稳定。当然由于金融数据本身的特点过于复杂,也意味着金融风险测度不会是一个简单的问题。虽然它的计算方法随着研究人员们的不断努力在不停地改善着,但时至今日,大部分的方法、模型也都是为VaR的测度研究提供参考。
基金项目
贵州民族大学科研资助项目。
文章引用
扶仕彤,金良琼. 基于分位数回归模型的VaR研究——以贵州百灵股票为例
VaR Research Based on Quantile Regression Model—Taking Guizhou Bailing Stock as an Example[J]. 统计学与应用, 2019, 08(02): 364-369. https://doi.org/10.12677/SA.2019.82040
参考文献
- 1. 张晨. VaR模型在我国金融风险管理中的运用研究[J]. 合肥工业大学学报:自然科学版, 2003, 26(3): 441-445.
- 2. 关静, 史道济. 分位数回归与上证综指VaR研究[J]. 统计与信息论坛, 2008, 23(12): 15-19.
- 3. Konenker, R. and Bassett, G. (1978) Regression Quantiles. Econometrica, 46, 33-50. https://doi.org/10.2307/1913643
- 4. 许启发, 徐金菊, 蒋翠侠. 基于神经网络分位数回归的多期CVaR风险测度[J]. 数理统计与管理, 2017, 36(4): 715-730.
- 5. 李治章, 王帅. 互联网金融对中国商业银行系统性风险溢出效应的测度——基于GARCH-CoVaR模型的研究[J].经济研究导刊, 2018(36): 50-53.
- 6. 许启发, 张金秀, 蒋翠侠. 基于非线性分位数回归模型的多期VaR风险测度[J]. 中国管理科学, 2015, 23(3): 56-65.
