Advances in Applied Mathematics
Vol.05 No.02(2016), Article ID:17704,12
pages
10.12677/AAM.2016.52038
Exponential Synchronization of Reaction-Diffusion Neural Networks with time Delay in the Leakage Term Based on Periodically Intermittent Control
Lili Wang, Rui Xu
Institute of Applied Mathematics, Shijiazhuang Mechanical Engineering College, Shijiazhuang Hebei

Received: May 4th, 2016; accepted: May 27th, 2016; published: May 30th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, the exponential synchronization of neural networks with spacial diffusion, mixed time-varying delays and leakage delay is investigated. By means of Lyapunov functional technique and some inequality techniques, exponential synchronization criteria dependent on leakage delay, diffusion coefficients and diffusion space are derived for the neural networks based on periodically intermittent control. The model studied in this paper is more general. The results obtained remove the restriction on the time-delays and are less conservative. Numerical simulations are carried out to illustrate the feasibility of the proposed theoretical results.
Keywords:Exponential Synchronization, Leakage Delay, Spacial Diffusion, Periodically Intermittent Control

一类具有Leakage时滞的反应扩散神经网络在间歇控制下的指数同步
王丽丽,徐瑞
军械工程学院应用数学研究所,河北 石家庄

收稿日期:2016年5月4日;录用日期:2016年5月27日;发布日期:2016年5月30日

摘 要
本文研究了一类具有混合时滞和Leakage时滞的反应扩散神经网络的指数同步问题。通过构造适当的Lyapunov泛函,结合不等式分析技巧,得到了系统在周期性间歇控制下实现指数同步的条件,且这些条件既依赖于Leakage时滞,又依赖于扩散系数和扩散空间。本文所研究的模型更具有一般性,所得结果去掉了对时滞的限制,降低了同步条件的保守性。最后通过数值模拟说明了所得结论的可行性。
关键词 :指数同步,Leakage时滞,反应扩散,间歇控制

1. 引言
近年来,由于混沌同步在保密通讯、信息处理、生命科学等领域的广泛应用,使得混沌同步控制成为人们研究的热点问题。人们提出了许多实现混沌同步的控制方法,例如自适应控制 [1] 、滑膜控制 [2] 、脉冲控制 [3] 、间歇控制 [4] 等。间歇控制和脉冲控制都是不连续的控制方法,脉冲控制是仅在某些点处加以控制,而间歇控制具有非零的控制宽度,因此间歇控制可以看作是脉冲控制与连续控制的过度,同时具备这两种方法的优点。与连续的控制方法相比,间歇控制降低了控制成本,在实际应用中更经济、有效、易于实现。正因如此,混沌系统在间歇控制下的指数同步问题已得到人们的广泛关注 [5] - [8] 。在文献 [8] 中,Xing等研究了一类具有离散时滞的递归神经网络在间歇控制下实现指数同步的问题:
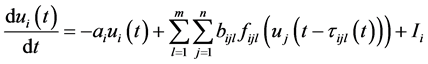 (1.1)
(1.1)
其中, ,
,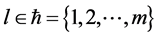 ,
,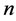 表示神经元的个数,
表示神经元的个数,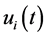 表示第
表示第 个神经元在
个神经元在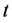 时刻的状态变量,
时刻的状态变量,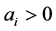 表示自反馈连接权,
表示自反馈连接权,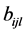 表示第
表示第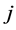 个神经元与第
个神经元与第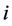 个神经元的连接权,
个神经元的连接权, 表示激励函数,
表示激励函数,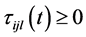 表示离散时滞,
表示离散时滞,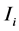 表示第
表示第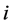 个神经元的外部输入。
个神经元的外部输入。
系统(1.1)被视作驱动系统,其响应系统为
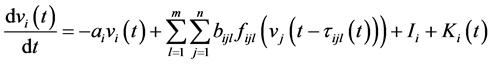 (1.2)
(1.2)
其中,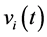 表示响应系统的第
表示响应系统的第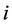 个神经元在
个神经元在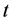 时刻的状态,
时刻的状态,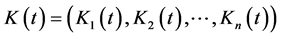 表示间歇控制器,系统中其它参数的意义与系统(1.1)相同。
表示间歇控制器,系统中其它参数的意义与系统(1.1)相同。
文献 [8] 给出了系统(1.1)和系统(1.2)实现指数同步的充分条件,所给的充分条件中要求离散时滞的导数小于1,即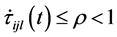 ,也就是要求离散时滞是慢变时滞,这显然是不符合实际情况的。另外,文献
,也就是要求离散时滞是慢变时滞,这显然是不符合实际情况的。另外,文献
[8] 只考虑了离散时滞对系统实现同步的影响,没有考虑空间扩散,分布时滞和Leakage时滞这些因素。事实上,当电子在一个非均匀的电磁场中运动时,扩散现象不可避免,也不能被忽视。而从空间上看,许多神经元的细胞体聚成球形或层状并相互作用,且通过轴突又连接成各种复杂的神经网络和神经通路,沿着这些路径就会出现传输时滞的分布。此时,信号传输不是即时的,不能用离散时滞来刻画,分布时滞更适宜刻画这种情形 [9] 。进一步,在实际的神经网络电路中,神经元的自衰减过程不是瞬时的,当神经元与神经网络和外部输入断开时,重置到隔离静止状态需要时间,为了刻画这种现象,有必要引入Leakage时滞。
基于上述讨论,本文将在文献 [8] 的基础上,研究下面的具有离散时滞,分布时滞和Leakage时滞的反应扩散神经网络在间歇控制下实现指数同步的问题,并降低同步条件的保守性:
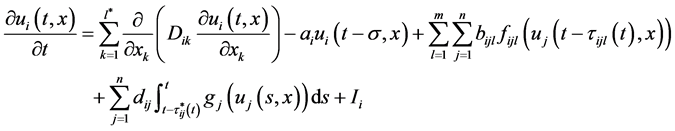 (1.3)
(1.3)
其中, ,
,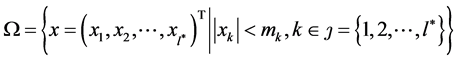 是具有光滑边界的紧集且测度
是具有光滑边界的紧集且测度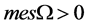 ,
,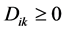 为扩散算子,
为扩散算子, 表示第
表示第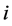 个神经元在
个神经元在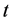 时刻和空间位置
时刻和空间位置 处的状态变量,
处的状态变量,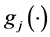 表示激励函数,
表示激励函数,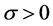 表示负反馈项时滞,
表示负反馈项时滞,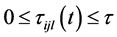 和
和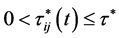 分别表示离散时滞和分布时滞,
分别表示离散时滞和分布时滞,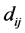 表示与分布时滞相关的第
表示与分布时滞相关的第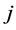 个神经元与第
个神经元与第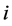 个神经元的连接权,模型中其他参数的意义与系统(1.1)相同。
个神经元的连接权,模型中其他参数的意义与系统(1.1)相同。
系统(1.3)满足以下的边界条件和初始条件:
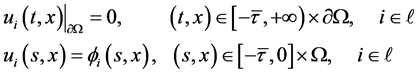 (1.4)
(1.4)
其中,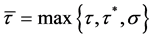 ,
,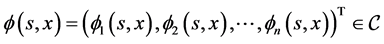 是有界连续函数,
是有界连续函数,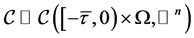 表示具有
表示具有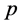 (
(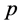 是正整数)范数的Banach连续函数空间,p-范数的定义为
是正整数)范数的Banach连续函数空间,p-范数的定义为
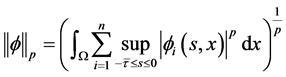
系统(1.3)是驱动系统,为了研究系统(1.3)的指数同步,我们引入响应系统为
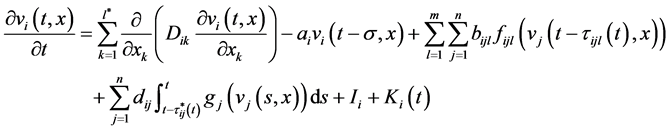 (1.5)
(1.5)
其中,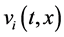 表示第
表示第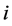 个神经元在
个神经元在 时刻和空间位置
时刻和空间位置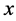 处的状态变量,
处的状态变量,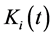 表示待设计的间歇控制器,定义为
表示待设计的间歇控制器,定义为
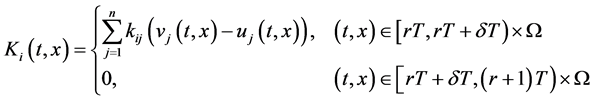 (1.6)
(1.6)
其中,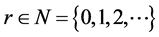 ,
, 为控制强度,且
为控制强度,且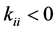 ,
,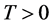 为控制周期,
为控制周期,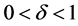 为切换率。模型中其他参数的意义与系统(1.3)相同。
为切换率。模型中其他参数的意义与系统(1.3)相同。
响应系统(1.5)满足下面的边界条件和初始条件:
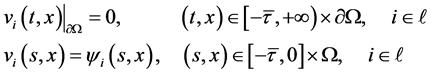 (1.7)
(1.7)
其中,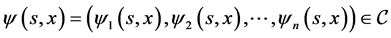 是有界连续函数。
是有界连续函数。
本文研究目的是设计合适的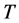 ,
,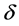 和
和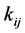 ,使得系统(1.3)和系统(1.5)在间歇控制器(1.6)下实现指数同步。我们的研究工作基于下面的假设:
,使得系统(1.3)和系统(1.5)在间歇控制器(1.6)下实现指数同步。我们的研究工作基于下面的假设:
(H1)激励函数 是Lipschitz连续的,即存在常数
是Lipschitz连续的,即存在常数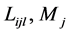 使得
使得
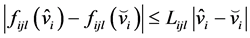 ,
,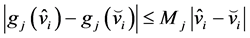
其中,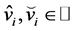 。
。
(H2)存在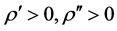 ,使得
,使得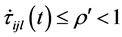 或
或 。
。
2. 预备知识
在本节中,我们引入证明中将用到的定义和引理。
定义2.1:若存在常数 和
和 ,使得
,使得
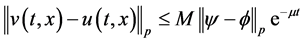 ,
,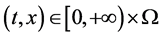
成立,则称系统(1.3)和系统(1.5)是基于p-范数指数同步的,其中
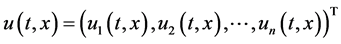

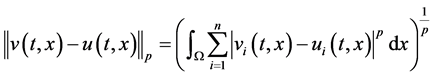
引理2.1 [10] :设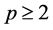 是正整数,
是正整数,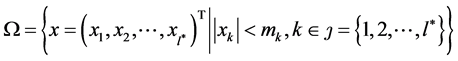 ,
,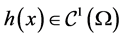 且满足
且满足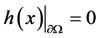 ,则
,则
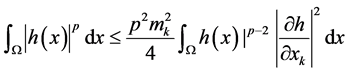
引理2.2 [11] :设 是连续函数,
是连续函数,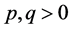 且满足
且满足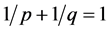 ,则
,则
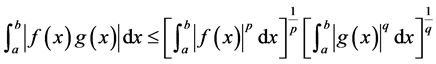
3. 主要结论
本节通过构造适当的Lyapunov泛函,给出系统(1.3)和系统(1.5)在间歇控制器(1.6)下实现指数同步的充分条件。
为了讨论方便,我们记:
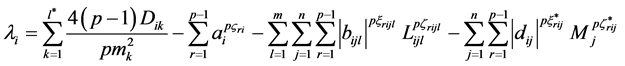
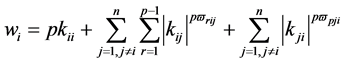 ,
, 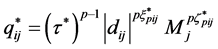
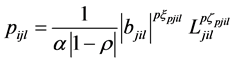 ,
, 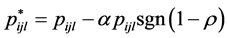 ,
, 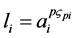
其中, ,
,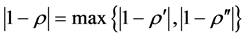 ,
,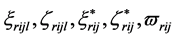 和
和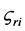 是非负实数,且分别满足
是非负实数,且分别满足
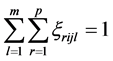 ,
,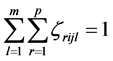 ,
,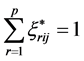 ,
,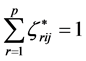 ,
,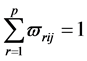 ,
,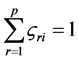
设

其中 。
。
若条件
(H3) 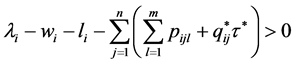
成立,则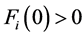 。因为
。因为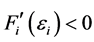 ,
,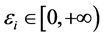 且当
且当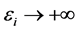 时,
时,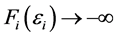 ,故由零点定理可知:存在唯一的
,故由零点定理可知:存在唯一的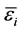 ,使得
,使得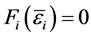 ,且
,且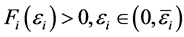 。
。
记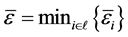 ,则
,则
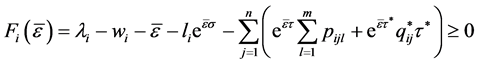 (3.1)
(3.1)
定理 3.1:若条件(H1)-(H3)成立,则当条件
(H4)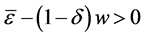 ,
,
成立时,系统(1.3)和系统(1.5)在间歇控制器(1.6)下是指数同步的。
证明:定义同步误差为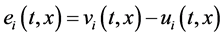 ,则由系统(1.3)和系统(1.5)可得
,则由系统(1.3)和系统(1.5)可得
 (3.2)
(3.2)
 (3.3)
(3.3)
其中,
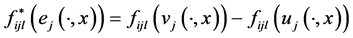

构造如下的Lyapunov-Krasovskii泛函:
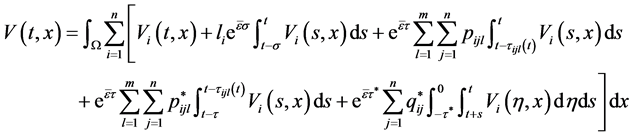 (3.4)
(3.4)
其中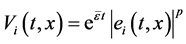 ,
,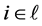 。
。
当 时,沿着系统(3.2)的解求
时,沿着系统(3.2)的解求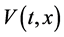 的Dini导数可得
的Dini导数可得
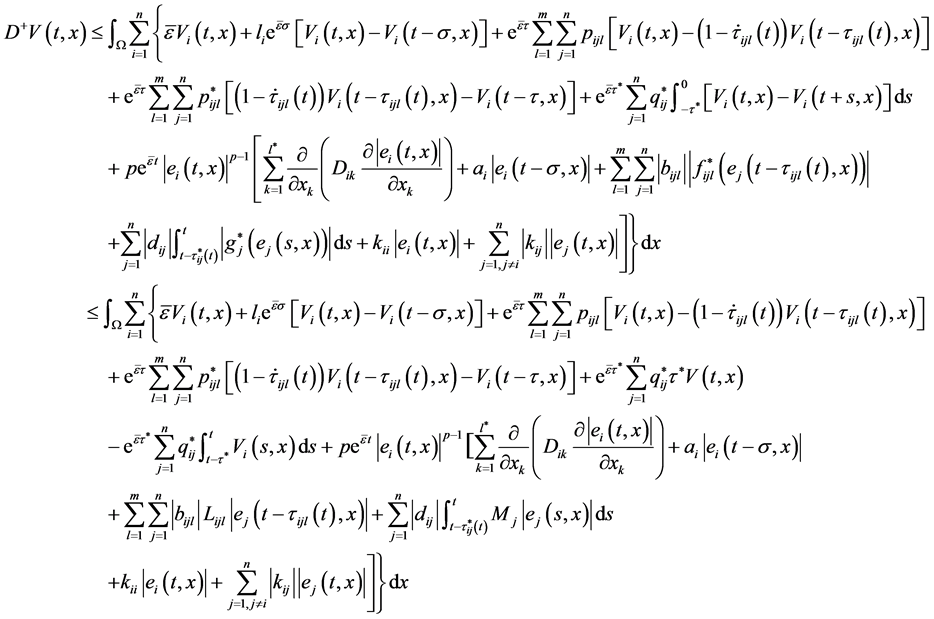 (3.5)
(3.5)
由引理2.2可得
 (3.6)
(3.6)
由边界条件(1.4),(1.7)和引理2.1可得
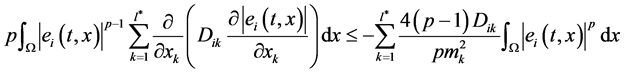 (3.7)
(3.7)
进一步,由于
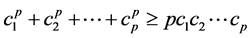 ,
,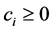 ,
,
所以
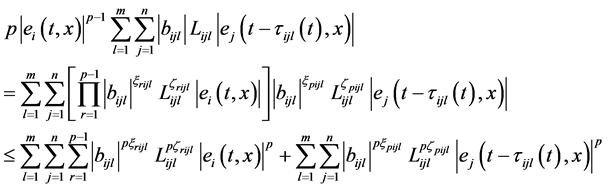 (3.8)
(3.8)
类似地,
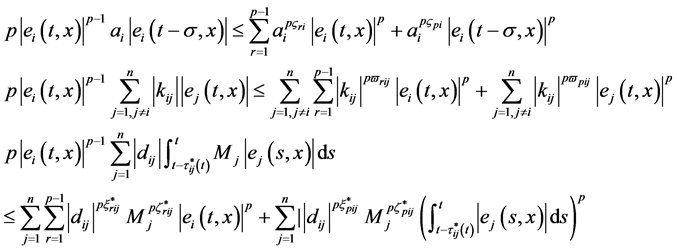 (3.9)
(3.9)
将(3.6)~(3.9)代入(3.5)可得
 (3.10)
(3.10)
由(3.1)和(3.10)可知
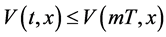 ,
, (3.11)
(3.11)
类似地,当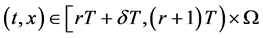 时,
时,
 (3.12)
(3.12)
由(3.12)可得
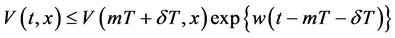 ,
,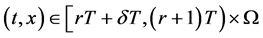 (3.13)
(3.13)
接下来,我们将使用数学归纳法证明对任意的正整数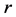 ,下面的不等式成立:
,下面的不等式成立:
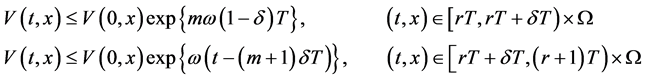 (3.14)
(3.14)
(1) 当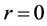 时,若
时,若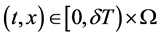 ,由(3.11)可知
,由(3.11)可知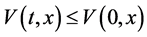 。
。
若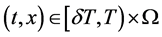 ,由(3.13)可知
,由(3.13)可知
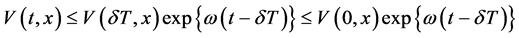
(2) 假设当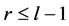 时,不等式(3.14)成立。
时,不等式(3.14)成立。
(3) 当 时,若
时,若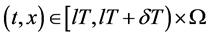 ,
,

若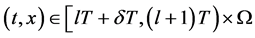 ,
,

综上所述,对任意的正整数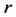 ,不等式(3.14)成立。
,不等式(3.14)成立。
根据(3.14)可知,若 ,则
,则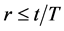 ,那么
,那么
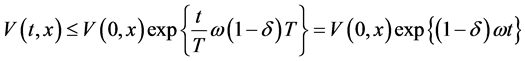 (3.15)
(3.15)
若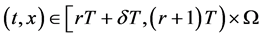 ,则
,则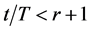 ,那么
,那么
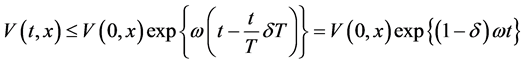 (3.16)
(3.16)
故由(3.15)和(3.16)可知,当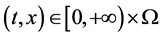 时,
时,
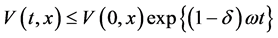 (3.17)
(3.17)
又由于
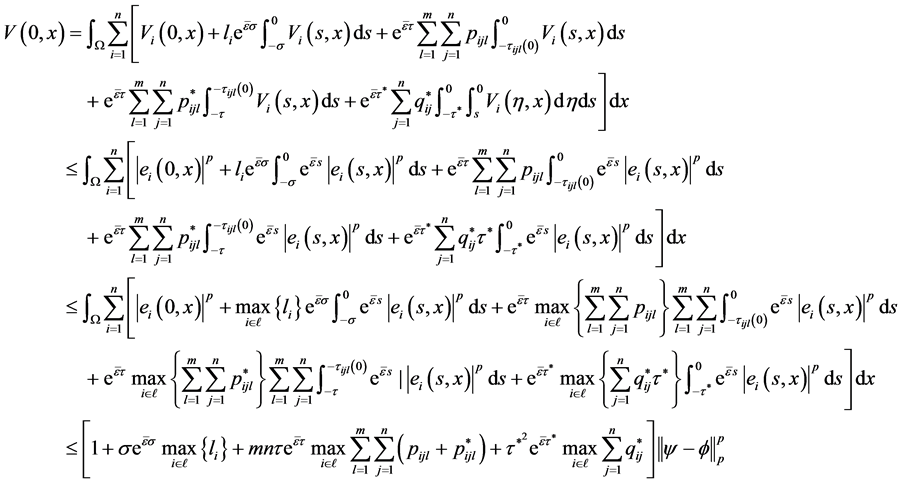
所以
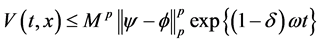 (3.18)
(3.18)
其中,
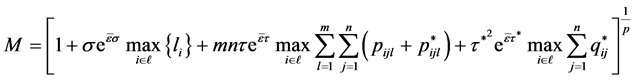
另一方面,
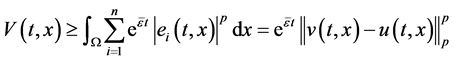 (3.19)
(3.19)
故由(3.18)和(3.19)得
 (3.20)
(3.20)
设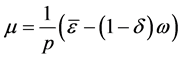 ,则
,则
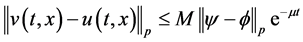
根据定义2.1可知系统(1.3)和系统(1.5)在间歇控制器(1.6)下是指数同步的。
注1文献 [6] ,文献 [7] 和文献 [8] 分别研究了几类时滞神经网络在间歇控制下的指数同步。文献 [6] 和文献 [8] 没有考虑分布时滞和反应扩散对系统实现指数同步的影响,文献 [7] 虽然考虑了上述因素,但分布时滞是常时滞。所以从这个意义上讲,文献 [6] ,文献 [7] 和文献 [8] 所研究的模型是本文的特殊情形,本文研究的模型具有一般性,更符合实际情况。
注2在文献 [6] ,文献 [7] 和文献 [8] 所给出的系统实现混沌同步的充分条件中,都要求时滞的导数小于1,也就是要求时滞是慢变的,实际上这是不必要而且也是不符合实际情况的,因为时滞的连续变化可能存在快变和慢变。而本文通过构造适当的Lyapunov泛函,去掉了对时滞的这一限制,因此降低了同步条件的保守性,所得结果也更具有普适性。
4. 数值模拟
在本节中,我们通过数值模拟说明定理3.1的可行性。
考虑如下具有两个神经元的驱动系统:
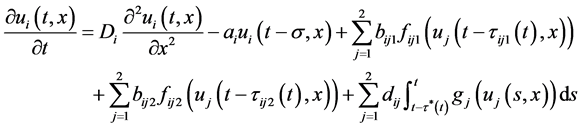 (4.1)
(4.1)
其中,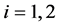 ,
,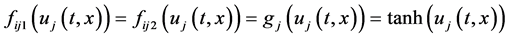 ,
,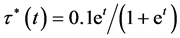 ,
,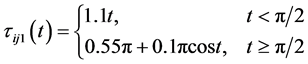 ,
,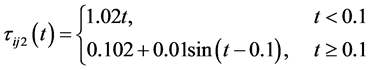 。选取连接权参数值为
。选取连接权参数值为 ,
, ,
,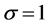 ,
, ,
,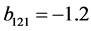 ,
, ,
,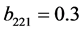 ,
,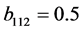 ,
,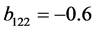 ,
,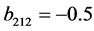 ,
, ,
,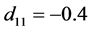 ,
,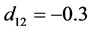 ,
,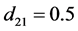 ,
, ,
, 。取初始条件为
。取初始条件为
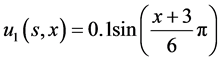 ,
, (4.2)
(4.2)
数值模拟表明系统(4.1)存在混沌现象(见图1)。
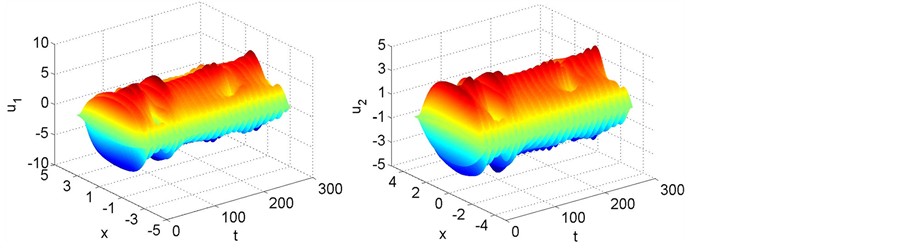
Figure 1. Chaotic behaviors of system (4.1) with initial conditions (4.2)
图1. 系统(4.1)满足初始条件(4.2)的混沌轨迹
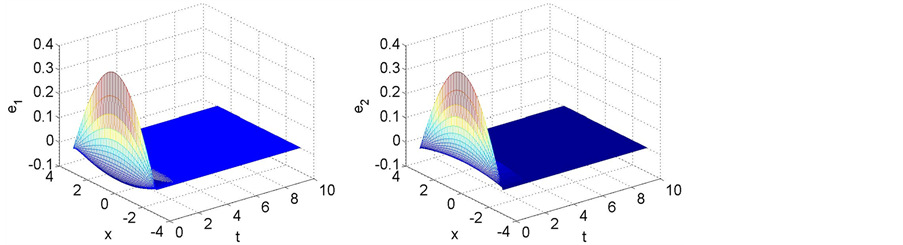
Figure 2. Dynamical behaviors of the synchronization errors between systems (4.1) and (4.3)
图2. 系统(4.1)和(4.3)的同步误差系统的动力学性态

Figure 3. Dynamical behaviors of the synchronization errors with different Leakage delays
图3. 同步误差系统在Leakage时滞取不同值时的动力学性态

Figure 4. Dynamical behaviors of the synchronization errors with different diffusion coefficients
图4. 同步误差系统在扩散系数取不同值时的动力学性态
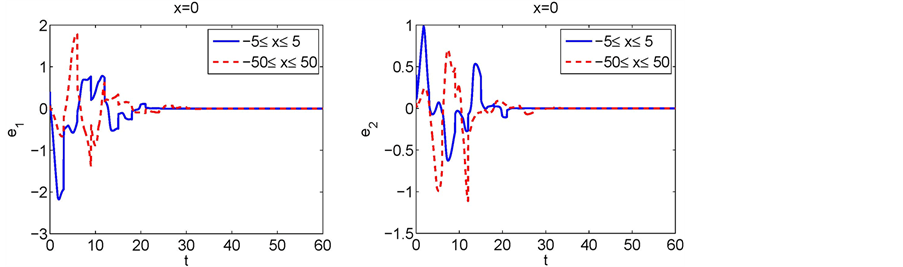
Figure 5. Dynamical behaviors of the synchronization errors with different space variables
图5. 同步误差在不同扩散空间下的动力学性态
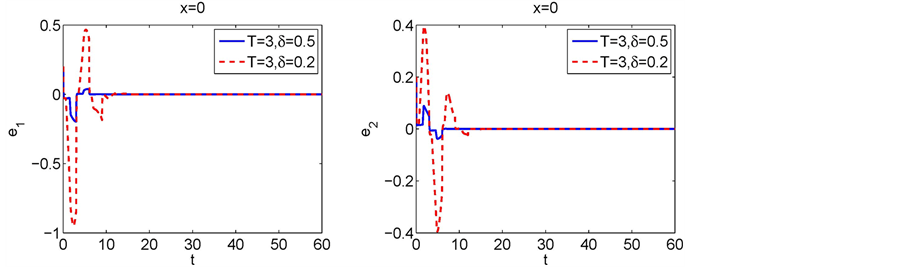
Figure 6. Dynamical behaviors of the synchronization errors with different control rate
图6. 同步误差在不同切换率下的动力学性态
系统(4.1)的响应系统为
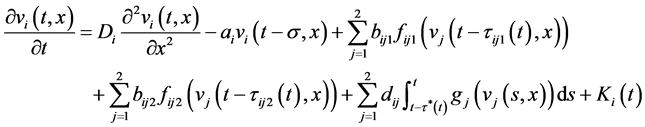 (4.3)
(4.3)
取初始条件为
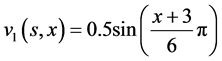 ,
,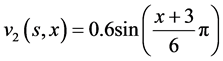 (4.4)
(4.4)
其中,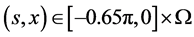 。
。
经计算可得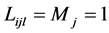 ,
,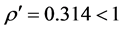 ,
, ,
,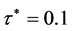 。可验证定理3.1中的条件(H1)~(H3)均满足。
。可验证定理3.1中的条件(H1)~(H3)均满足。
设 ,
, ,
,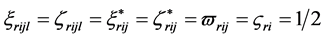 ,控制参数为
,控制参数为 ,
,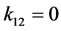 ,
,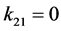 ,
,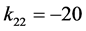 ,
,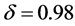 ,
,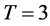 ,则
,则
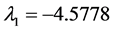 ,
,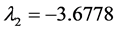 ,
,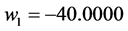 ,
,
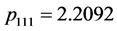 ,
,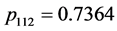 ,
,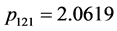 ,
,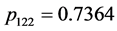 ,
,
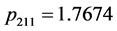 ,
,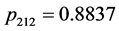 ,
, ,
, ,
,
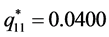 ,
,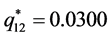 ,
, ,
,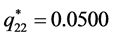 ,
,
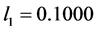 ,
,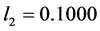
经计算可得 ,
,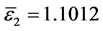 ,所以
,所以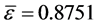 ,
, 。容易验证定理3.1中的条件(H4)成立。由定理3.1可知,驱动系统(4.1)和响应系统(4.3)在所给出的间歇控制器下是指数同步的。数值模拟验证了我们的结果(见图2)。
。容易验证定理3.1中的条件(H4)成立。由定理3.1可知,驱动系统(4.1)和响应系统(4.3)在所给出的间歇控制器下是指数同步的。数值模拟验证了我们的结果(见图2)。
定理3.1给出了系统(1.3)和系统(1.5)在间歇控制器(1.6)下实现混沌同步的充分条件。很显然,所给出的同步条件依赖于Leakage时滞,反应扩散系数,反应扩散空间和切换率。从定理3.1可以看出,较小的Leakage时滞,较大的扩散系数 ,较小的扩散空间
,较小的扩散空间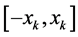 以及较大的切换律,均可以使系统更容易实现同步。数值模拟验证了我们的结论(见图3~6)。
以及较大的切换律,均可以使系统更容易实现同步。数值模拟验证了我们的结论(见图3~6)。
基金项目
本文受到国家自然科学基金(11371368),国家自然科学基金(61305076),军械工程学院基础部科学研究基金(Jcky1507)等项目资助。
文章引用
王丽丽,徐瑞. 一类具有Leakage时滞的反应扩散神经网络在间歇控制下的指数同步
Exponential Synchronization of Reaction-Diffusion Neural Networks with time Delay in the Leakage Term Based on Periodically Intermittent Control[J]. 应用数学进展, 2016, 05(02): 298-309. http://dx.doi.org/10.12677/AAM.2016.52038
参考文献 (References)
- 1. Dai, D. and Ma, X.K. (2011) Chaos Synchronization by Using Intermittent Parametric Adaptive Control Method. Physics Letters A, 288, 23-28. http://dx.doi.org/10.1016/S0375-9601(01)00521-7
- 2. Yahyazadeh, M., Noei, A.R. and Ghaderi, R. (2011) Synchronization of Chaotic Systems with Known and Unknown Parameters Using a Modified Active Sliding Mode Control. ISA Transactions, 50, 262-267. http://dx.doi.org/10.1016/j.isatra.2010.10.009
- 3. Li, X.D. and Song, S.J. (2014) Research on Synchronization of Chaotic Delayed Neural Networks with Stochastic Perturbation Using Implusive Control Method. Communications in Nonlinear Science and Numerical Simulation, 19, 3892-3900. http://dx.doi.org/10.1016/j.cnsns.2013.12.012
- 4. Huang, J.J., Li, C.D. and Han, Q. (2009) Stabilization of De-layed Chaotic Neural Networks by Periodically Intermittent Control. Circuits, Systems, and Signal Processing, 28, 567-579. http://dx.doi.org/10.1007/s00034-009-9098-3
- 5. Gan, Q.T. (2012) Exponential Synchronization of Stochastic Cohen-Grossberg Neural Networks with Mixed Time- Varying Delays and Reaction-Diffusion via Periodi-cally Intermittent Control. Neural Networks, 31, 12-21. http://dx.doi.org/10.1016/j.neunet.2012.02.039
- 6. Hu, C., Yu, J., Jiang, H.J. and Teng, Z.D. (2010) Exponential Stabilization and Synchronization of Neural Networks with Time-Varying Delays via Periodically Intermittent Control. Nonlinearity, 23, 2369-2391. http://dx.doi.org/10.1088/0951-7715/23/10/002
- 7. Hu, C., Yu, J., Jiang, H.J. and Teng, Z.D. (2012) Exponential Synchronization for Reaction-Diffusion Networks with Mixed Delays in Terms of p-Norm via Intermittent Control. Neural Networks, 31, 1-11. http://dx.doi.org/10.1016/j.neunet.2012.02.038
- 8. Xing, J.J., Jiang, H.J. and Hu, C. (2013) Exponential Syn-chronization for Delayed Recurrent Neural Networks via Periodically Intermittent Control. Neucomputing, 82, 122-129. http://dx.doi.org/10.1016/j.neucom.2013.01.041
- 9. Zhou, P.P. and Chen, F.Q. (2011) Existence of Periodic Solutions for Bidirectional Associative Memory Neural Networks with Distributed Delays. Acta Analysis Functionalis Applicata, 13, 145-153.
- 10. Hu, C., Jiang, H.J. and Teng, Z.D. (2010) Impulsive Control and Synchronization for Delayed Neural Networks with Reaction-Diffusion Terms. IEE Transactions on Neural Networks, 21, 67-81. http://dx.doi.org/10.1109/TNN.2009.2034318
- 11. Mao, X. (2006) Stochastic Differential Equations and Appli-cations. Horwood Publication, Chichester.