Advances in Applied Mathematics
Vol.07 No.04(2018), Article ID:24707,6
pages
10.12677/AAM.2018.74053
Judicious Balanced Bipartitions of (k, k − 1)-Biregular Graphic Degree Sequence
Haiyan Li, Jin Guo
College of Information Science and Technology, Hainan University, Haikou Hainan

Received: Apr. 11th, 2018; accepted: Apr. 21st, 2018; published: Apr. 28th, 2018

ABSTRACT
Let be a graphic sequence of nonnegative integers and are two sequences that are obtained by partitioning the elements of π into two sets. A balanced bipartition of π is a bipartition such that , where is denoted to the number of elements of . In this paper, let k and m be positive integers, we determine the values and of -biregular graphic sequence .
Keywords:Graph, Degree Sequence, -Biregular Graphic Sequence, Judicious Balanced Bipartition

(k, k − 1)-双正则可图序列的公平划分
李海燕,郭锦
海南大学信息科学技术学院,海南 海口

收稿日期:2018年4月11日;录用日期:2018年4月21日;发布日期:2018年4月28日

摘 要
设 是非负整数序列, 是将 的所有元素划分为两部分后的两个子序列。如果 ,则称 是 的一个平衡二部划分,其中 表示 中的元素数目。设k和m是两个正整数, 是双正则可图序列。本文确定了 的值和 的值。
关键词 :图,度序列, -双正则可图序列,公平划分

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文中只限于讨论有限简单图。未给出的定义请参照文献 [1] 。设G和H是简单图,图 表示G与H的和,其顶点集为 ,其边集为 。
设 是图G的一个二部划分,如果 ,则称 是G的一个二部平衡划分。对于 , 表示两个端点都在 中的边的数目, 表示两个端点分别在顶点子集 中的边数。通常 用来表示平衡二部划分的大小。图G的一个最大(最小)平衡二部划分 是图G的所有平衡二部划分中 的值达到最大(最小)。与最大,最小平衡划分问题不同,公平划分问题是寻找图G的一个划分,使得多个分量同时进行优化。
本文将把图的公平划分问题变形到度序列的公平划分问题。
若简单图有顶点集 且 的度为 ,则序列 称为G的度序列。记 为所有满足 的整数序列的集合。如果π是某个n阶简单图G的度序列,那么称π为可图序列,且G为π的一个实现。记 为 中的所有可图序列组成的集合。在可图度序列中, 表示有n个r,即度序列的实现中有n个顶点的度为r。
给定可图序列π, 是将π的元素划分为两部分后的两个子序列。如果 ,则称 是π的一个平衡二部划分,其中 表示 中的元素数目。若G是π的一个实现, 是G的一个平衡二部划分且 在π中的度序列分别为 ,则称 为π的平衡二部划分 的一个实现。
类似于图的“公平”划分问题,我们考虑度序列的“公平”划分问题:寻找已知可图序列π的一个平衡二部划分 ,使得 的某个实现 在π的所有平衡二部划分的所有实现下 达到最大或者 达到最小,记 , 。若 是π的某个平衡二部划分的一个实现,显然 , 。
2. 主要定理及引理
定理2.1:(Erdös和Gallai [2] )设 且 是偶数。则 当且仅当对任意整数t,
都成立。
设
,
是两个非负整数序列。如果存在一个简单二部图
使得X和Y中的顶点度分别是
和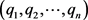 ,那么称序列对
,那么称序列对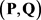 是二部可图的,并称二部图
是二部可图的,并称二部图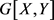 为
为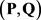 的一个实现。Gale [3] 和Ryser [4] 分别独立地给出了关于二部可图序列的刻划定理。
的一个实现。Gale [3] 和Ryser [4] 分别独立地给出了关于二部可图序列的刻划定理。
定理2.2:(Gale [3] , Ryser [4] ) 设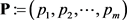 和
和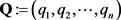 是两个非负整数序列且满足
是两个非负整数序列且满足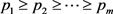 ,
,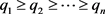 。若
。若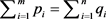 ,则
,则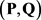 是二部可图的当且仅当
是二部可图的当且仅当
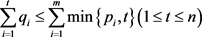
成立。
引理2.3:(Yin和Li [5] )设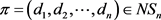 ,
, 且
且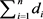 是偶数。如果
是偶数。如果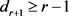 ,则
,则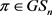 。
。
设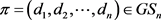 ,若
,若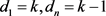 ,则称π是
,则称π是 -双正则可图的。本文主要给出双正则可图序列
-双正则可图的。本文主要给出双正则可图序列 的公平划分的上下界。
的公平划分的上下界。
3. (k, k − 1)-双正则可图序列的公平划分 的上界
的上界
定理3.1:设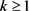 是一个正整数,m是4的整数倍且
是一个正整数,m是4的整数倍且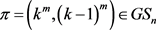 。那么
。那么
1) 若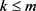 ,则
,则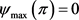 ;
;
2) 若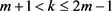 ,则
,则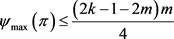 。
。
证明:情形(1):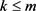 。
。
设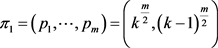 ,
,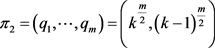 ,那么
,那么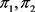 是π的一个平衡二部
是π的一个平衡二部
划分。这里,
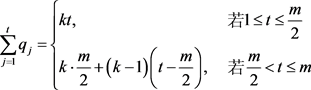 (1)
(1)
且
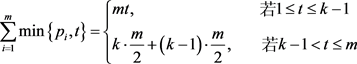 (2)
(2)
接下来我们比较 和
和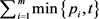 的大小。显然,由(1)和(2)得
的大小。显然,由(1)和(2)得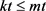 且
且
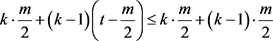 。
。
若 ,由(1)和(2)得,
,由(1)和(2)得,
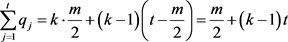 ;
;
 。
。
据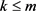 和
和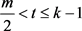 可得
可得
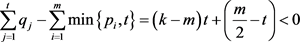 。
。
若 ,由(1)和(2)得,
,由(1)和(2)得,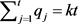 ;
;
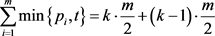 。
。
显然,
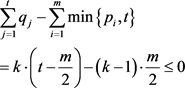 。
。
由定理2.2, 是二部可图的。设
是二部可图的。设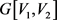 是
是 的一个实现,则G也是
的一个实现,则G也是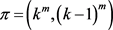 的一个实现且
的一个实现且 是G的一个平衡二部划分。因此,
是G的一个平衡二部划分。因此,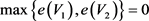 。
。
故,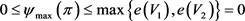 ,且
,且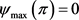 。
。
情形(2):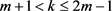 。
。
设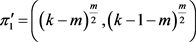 ,
,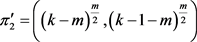 。由于
。由于 是偶数,所以
是偶数,所以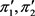 的度和
的度和 为偶数。由引理2.3知,
为偶数。由引理2.3知, 。设
。设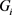 是
是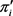 的一个实现且
的一个实现且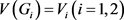 ,
,
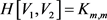 。令
。令 。容易验证G是π的一个实现,且
。容易验证G是π的一个实现,且
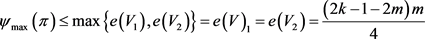 。
。
证毕。
4. (k, k-1)-双正则可图序列的公平划分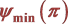 的下界
的下界
定理4.1:设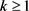 是一个正整数,m是4的整数倍且
是一个正整数,m是4的整数倍且 。那么
。那么
1) 若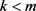 ,则
,则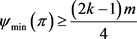 ;
;
2) 若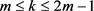 ,则
,则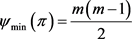 。
。
证明:情形(1):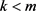 。
。
设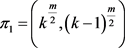 ,
,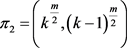 ,则
,则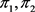 是π的一个平衡二部划分。由于
是π的一个平衡二部划分。由于 是偶数,所以
是偶数,所以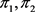 的度和
的度和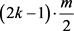 为偶数。又由引理2.3可得,
为偶数。又由引理2.3可得,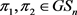 。设
。设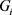 是
是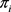 的一个实现且
的一个实现且
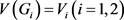 ,令
,令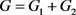 。容易验证G是π的一个实现,
。容易验证G是π的一个实现,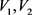 是G的一个平衡二部划分且
是G的一个平衡二部划分且
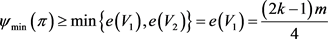 。
。
情形(2):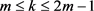 。显然
。显然 。
。
设 ,
,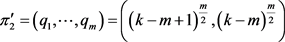 。这里,
。这里,
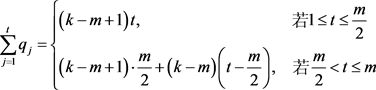 (3)
(3)
且
 (4)
(4)
接下来我们比较 和
和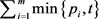 的大小。显然,由(3)和(4)得
的大小。显然,由(3)和(4)得 且
且
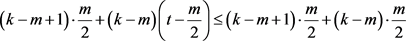 。
。
若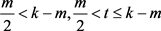 ,由(3)和(4)得,
,由(3)和(4)得,
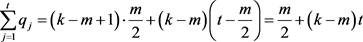 ;
;
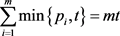 。
。
据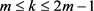 和
和 可知
可知

若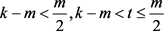 ,由(3)和(4)得,
,由(3)和(4)得,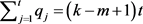 ;
;
 。
。
显然,
 。
。
由定理2.2,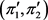 是二部可图的。设
是二部可图的。设 是
是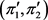 的一个实现,
的一个实现,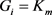 且
且 。令
。令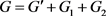 ,则G是
,则G是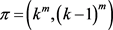 的一个实现且
的一个实现且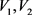 是G的一个平衡二部划分。故,
是G的一个平衡二部划分。故,
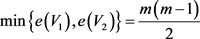 。
。
因此,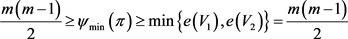 ,
,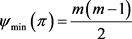 。证毕。
。证毕。
基金项目
海南省自然科学基金(No. 20161003, 20161002);国家自然科学基金(No. 11601108)。
文章引用
李海燕,郭 锦. (k,k-1)-双正则可图序列的公平划分
Judicious Balanced Bipartitions of (k,k-1)-Biregular Graphic Degree Sequence[J]. 应用数学进展, 2018, 07(04): 423-428. https://doi.org/10.12677/AAM.2018.74053
参考文献
- 1. Bondy, J.A. and Murty, U.S.R. (1976) Graphy Theory with Applications. Macmillan Ltd Press, New York. https://doi.org/10.1007/978-1-349-03521-2
- 2. Erdös, P. and Gallai, T. (1960) Graphs with Prescribed Degrees of Vertices. Matematikai Lapok, 11, 264-274.
- 3. Gale, D. (1957) A Theorem on Flows in Networks. Pacific Journal of Mathematics, 7, 1073-1082. https://doi.org/10.2140/pjm.1957.7.1073
- 4. Ryser, H.J. (1957) Combinatorial Properties of Matrices of Zeros and Ones. Canadian Journal of Mathematics, 9, 371-377. https://doi.org/10.4153/CJM-1957-044-3
- 5. Yin, J.H. and Li, J.S. (2005) Two Sufficient Conditions for a Graphic Sequence to Have a Realization with Prescribed Clique Size. Discrete Mathematics, 301, 218-227. https://doi.org/10.1016/j.disc.2005.03.028