Advances in Applied Mathematics
Vol.
08
No.
01
(
2019
), Article ID:
28656
,
10
pages
10.12677/AAM.2019.81018
Detecting the Early Warning Signals of Disease Progression Based on Individual Difference Time Series Network
Xiaoling Guan
School of Mathematics, South China University of Technology, Guangzhou Guangdong

Received: Jan. 2nd, 2019; accepted: Jan. 21st, 2019; published: Jan. 28th, 2019

ABSTRACT
Pre-disease state is a critical stage of the disease state. Patients in this state can return to the normal state as long as they receive reasonable and effective treatment. Therefore, it is of great significance for medical workers and patients to detect the pre-disease state. In this paper, an algorithm is developed to establish the sampling-specific temporal differential network (SSDN) based on the individual single sample, and according to the sampling-specific temporal differential network, the signal of disease progression can be detected effectively. The validity of the method is verified by numerical simulation and two real data.
Keywords:Single Sample, Temporal Differential Network, Dynamic Network Biomarkers, Composite Variable, Critical-Point
基于个体时序列差异网络探测疾病恶化 的预警信号
关小玲
华南理工大学数学学院,广东 广州

收稿日期:2019年1月2日;录用日期:2019年1月21日;发布日期:2019年1月28日

摘 要
前疾病状态是疾病状态的一个临界期,处于这个状态的患者,只要经过合理有效的治疗,就可以回到正常状态。所以,探测前疾病状态对于医疗工作者以及病人来说有着极其重要的意义。本文开发了一种算法,基于个体单样本建立个体时序列差异网络,并根据所建立的个体时序列差异网络,可以有效地探测疾病恶化的信号。该方法的有效性得到了数值模拟和两个真实数据的检验。
关键词 :个体单样本,时序列差异网络,动态网络生物标志物,复合变量,临界点

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
考虑到人类细胞中分子组分之间的功能相互依赖性,疾病表型很少是单个生物分子发生异常表达的结果,而是由基因、蛋白质和代谢物等相关因素共同作用导致的,它们所构成的复杂相互作用网络,是我们用来研究生物疾病进展的有效依据 [1] [2] 。因此,了解生物分子相互作用网络的动态变化,对于全面研究复杂疾病的进展,从而更好地检测相关疾病的预警信号具有重要意义。
已有理论表明,处于前疾病状态和正常状态的生物系统在分子表达上是静态相似的,但在动力学上不同 [3] [4] [5] ,利用这些动态差异的特征,探索正常状态和前疾病状态的分子间的差异关联信息,可以有效地识别出处于前疾病状态的系统。本文基于单样本结合差异网络开发了一种新的检测疾病恶化的预警信号的方法,即利用时间进程数据构建一系列个体特异网络,获得相邻时间点个体特异网络的时序差异信息,进而得到个体时序列差异网络,用以整合具有时间上不同特征的生物分子,包括具有差异表达方差的基因和具有差异表达协方差的基因对之间的相互作用。由此从个体时序列差异网络的角度系统地展示了生物系统发展的动态变化,可以准确地描述个体的特定疾病状态。
为了更好的量化这些动态差异并准确地识别临界点,我们提出了一个复合变量I,作为用于识别即将到来的临界点的特定标识符,I的快速上升预示着前疾病状态的出现,而在正常状态或疾病状态中平稳地发展,I几乎没有显著波动。为了验证方法的有效性,我们将之应用于一个数值仿真实验和两个从NCBI的GEO数据库(https://www.ncbi.nlm.nih.gov/geo/)下载得到真实疾病数据集,即前列腺癌数据(GSE 5345)和肝癌数据(GSE 80018)。通过计算发现,两种疾病发生恶化的早期预警信号出现的时间与实验观察结果一致。
2. 方法
2.1. 个体差异性时序网络的构造
当样本数量少甚至只有一个样本时,我们无法计算出样本的皮尔逊相关系数。而通过利用单样本动态网络标志物的方法可以解决这个问题。本文所述的用个体时序列差异网络检测复杂疾病恶化的临界信号方法的主要步骤如下(图1):
1) 构造个体特异网络(Sampling-specific differential network, SSN) (图1(a))。首先,利用疾病数据,选定适量正常的样本作为参考样本,并利用样本的两两基因间的皮尔逊相关系数,作为两个基因节点的边 [6] ,构造参考样本网络。其次,通过把单个样本加到参考样本里,通过两两基因间的皮尔逊相关系数构造扰动样本网络。最后,对比参考网络和扰动网络,根据z-score,保留两个网络共有的具有显著表达的边,进而得到个体特异网络 [1] 。
2) 构造个体时序列差异网络(图1(b))。对比两两相邻时间点的个体特异网络,保留它们的差异边,得到个体差异性时序网络(Sampling-specific temporal differential network, SSDN)。
3) 由步骤二,得到个体时序列差异网络(图1(c)),结合差异网络中边和网络节点的特性,用一个复合变量检测出复杂疾病发生病变的临界点。
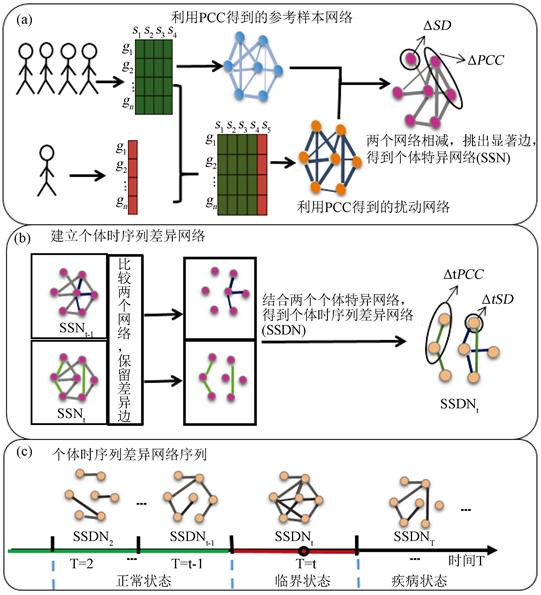
Figure 1. Flow chart of construction of sample-specific temporal differential network
图1. 个体时序列差异网络的构造的流程图
2.2. 基于动态网络标志物的复合变量
基于2.1,得到的单样本动态网络标志物满足以下两个条件:
1) 单样本动态网络标志物中两两元素所构成的个体时序列差异网络边的皮尔逊相关系数的绝对值
均数 大幅增加;
2) 单样本动态网络标志物中任意元素的表达方差的差的绝对值( )的大幅增加。
引入复合变量
其中, 表示个体时序差异网络SSDN中显著边的皮尔逊相关系数的绝对值的和的,N即表示SSDN中显著边的数量。 表示SSDN中基因节点的标准差的绝对值。对以上复合变量I进行验算,若I的值在某点处急剧上升并达到峰值时,表示该点为疾病发生病变的临界点。
3. 主要结果
3.1. 八个节点的仿真数据
在这里,为了检测方法的有效性,我们使用八个基因节点网络(图2,节点间的连线表示基因间的调控关系,其中箭头线表示正调节,钝化线表示负调节)进行数值模拟,并从理论上论证了通过复合变量I可以检测复杂疾病的预警信号。这种类型的基因调控网络常常应用于研究基因转录、翻译等影响基因调控的活动。下面的八个微分方程表示网络中八个基因的一般规律 [7] ,其中基因调控以Michaelis-Menten方程加入基因自身的降解率的形式表示,降解率与相应基因浓度成线性比例关系。
(1)
微分方程系统(1)中的P表示的是标量控制参数, 是均值为零,方差为 的高斯噪声, 表示基因的表达浓度。八个基因的降解率分别为 。从微分系统(1)可以看出,系统有一个稳定的平衡点 。运用欧拉序列,可以把微分方程转换成 的形式,即
(2)
表示微小的时间间隔,注意到 是 在 时刻的向量。我们把差分系统(1)的雅可比矩阵用 表示,其中
(3)
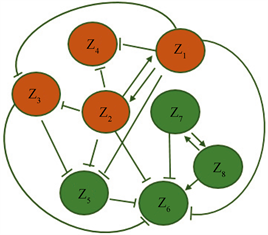
Figure 2. Eight gene regulatory networks and their differential equations
图2. 八个基因的调控网络及其微分方程系统
这里A为微分方程线性系统的系数矩阵,并且矩阵A的八个不同的特征值组成的向量为
。
对于矩阵J,存在一个非退化矩阵
满足 。明显地,当 时, ,这时差分系统(1)的状态失去原有的稳定性,发生临界转变。所以,当 ,系统在临界点 是稳定的。我们的目标是检测当控制参数P从 接近临界值0的时候,系统状态发生转变的一个早期预警信号。利用公式 ,我们可以得到
可知 中的四个变量 是与 直接相关的,根据已有的理论可知, 构成了八个结点仿真网络系统的主要部分,即相当于真实数据中的动态网络生物标志物。
在这里,为了检测方法的有效性,我们使用八个基因节点网络(图2,节点间的连线表示基因间的调控关系,其中箭头线表示正调节,钝化线表示负调节)进行数值模拟,并从理论上论证了通过复合变量I。
基于仿真模型,采集得到了12个样本在41个时间点下的八个基因节点的数据,其中容易知道,第21个时间点为我们所模拟的临界点。在这次的仿真数据中,参考样本选取来自于第一个时间点的任意6个样 本,疾病样本取自剩余的6个样本中的任3个,正常样本则为最后的3个样本,并且把这三个样本在第21个时间点的数据用第一个时间点的任意三个样本的数据替换掉,以保证每一个正常样本与疾病样本区分开来。然后根据这些模拟数据计算出个体时序列差异网络的复合变量I,得到以图3(a)的折线图,红色曲线代表由3个疾病样本计算得到的复合变量的平均值,绿色曲线表示3个由正常样本计算得到的的复合变量的平均值。图3(b)的3个网络表示个体样本在p = −0.3,p = −0.02和p = 0.3处的个体时序列差异网络,分别处于正常状态,前疾病状态和疾病状态,它们都是分别由处于三个不同状态的两个相邻时间点的个体特异网络得到的。在每个个体时序差异网络中,连接两个节点的边代表的是时间差异相关性。由图3可以容易得到,p = 0的点为系统状态临界转换点。
由实验结果可知,此实验验证了复合变量I在临界状态信号传递过程中的可靠性和准确性。因此,基于个体时序列差异网络,复合变量I能够利用高维信息来区分前疾病的样本和正常样本。
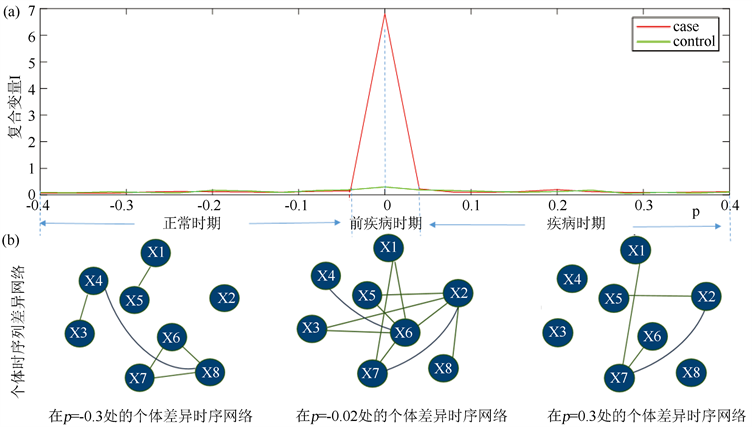
Figure 3. The line chart of numerical simulation and the sample-specific temporal differential network
图3. 数值模拟结果折线图和个体时序列差异网络
3.2. 方法应用于两个真实的疾病数据
本节我们把这个方法运用到两个来源于NCBI的GEO数据库(https://www.ncbi.nlm.nih.gov/geo/)的真实数据,即前列腺癌数据(GSE5345)和肝癌数据(GSE80018)。通过建立个体特异时序差异网络的方法,我们把每个时间点都当作是候选的临界转化点。
前列腺癌的数据是通过前人的工作实验而得到的。实验工作者把用合成雄激素培养的前列腺癌细胞系(LNCaP)作为实验组,把用乙醇培养的前列腺癌细胞LNCaP作为对照组,分别在0、6、9、12、18、24、48小时分离RNA并采集基因表达数据。使用合成的雄激素R1881刺激人体的前列腺癌细胞系LNCaP 的24小时内,部分RNA表达水平下调2-3倍直至48小时后恢复正常,部分上调2~3倍甚至3~6倍后恢复正常 [8] 。
基于前列腺癌的数据,利用2中的方法,计算每一个样本的复合变量I,可以得到4个样本都在24小时处出现临界转变信号(图4(a)),并且他们的动态网络标志物的数量分别为246,239,217,201,其中4个样本之间两两共有的动态网络生物标志物的数量分别是66,18,10,11,16,76,一共得出164个基因作为识别前列腺癌临界转变的动态网络标志物,图4(c)表示这164个差异表达基因在临界点前后时间点的动态翻转网络。图4(b)的圆盘图分别展示了分子网络在0 h,9 h,12 h,18 h,24 h和48 h的动态变化。每一个网络都是基于表达数据的人体前列腺基因相互作用网络构建的。节点的颜色表示基因表达的波动情况,每个网络中左上角表示164个差异表达最显著的基因。从圆盘图中可以看出,所选择的基因在24 h处表达波动最激烈,在这一时期其网络结构变化最为显著。因此,可以得出,前列腺癌病变的临界时间点在24 h处,与实验观测以及数值计算结果相吻合。
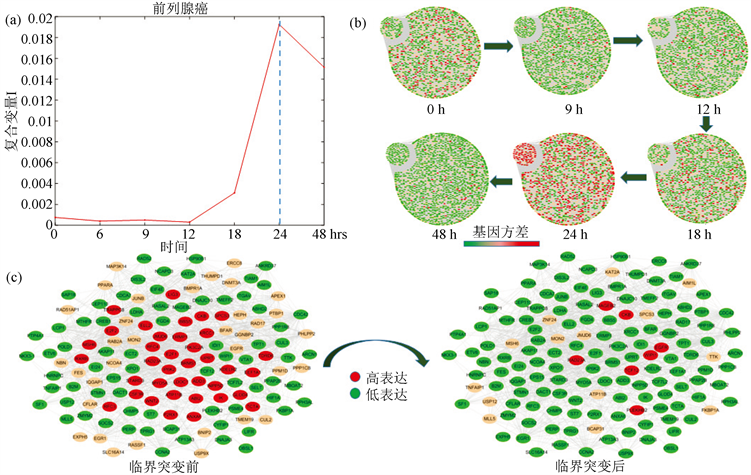
Figure 4. The line chart of early-warning signals, the dynamically changes in the network and overturn network during the progression of prostate cancer
图4. 前列腺癌临界信号折线图,分子网络动态变化以及翻转网络图
对肝癌数据,是由实验工作人员随机给雄性小鼠分为两组,把用含有0.05% [wt/vol]苯巴比妥(Phenobarbital, PB)饮用水喂养的那组作为实验组,把用不含PB的正常饮用水喂养的那组作为对照,并在第1、3、7、14、28,57和91天后对小鼠进行处理并收集小鼠的肝脏基因表达数据而得到的,以用来研究PB对小鼠的影响。通过实验观测可知,在PB处理的第1天,检测到肝脏切片有短暂的有丝分裂反应,而且最显著的病理异常表现为肝细胞在第7天后开始变得肥大,且在后期严重程度增加。PB处理影响了肝脏中大量基因的转录,其中PB诱导的异型生物代谢酶,包括CYP450酶和POR还原酶,从利用PB处理第1天开始,它们的蛋白水平在整个表达过程中均发生上调 [9] 。
利用本文开发的方法,基于5个样本分别计算它们的复合变量I,发现5个样本都在第3天出现早期疾病预警信号,由此可知,5个样本的状态都在第3天发生转变(图3(b))。并得到5个样本的动态网络标志物的数量分别为181,189,178,185,204,其中5个样本之间两两共有的动态网络生物标志物的数量分别有6,6,11,17,15,12,2,30,30,16,一共有87个基因。图5(b)表示这87个差异表达基因在临界时间点前后的动态翻转网络。
4. 讨论
本文基于单样本生物动态网络的性质,从生物数据中提取生物系统中的一些动态信息,即通过对比相邻时间点的个体特异网络,提取它们之间边的相关性以及基因的表达方差等,从而获得疾病发病密切相关的主要基因,最终识别疾病进展过程中的临界状态或者是临界点,达到预测疾病的目的。基于前列腺癌数据,本文所用到的方法成功地探测出了第六个时间点为疾病恶化的临界时间点。同样,对于肝癌数据,我们也成功地探测出第二个时间为疾病恶化的临界点。这些探测结果与实验结果相一致。
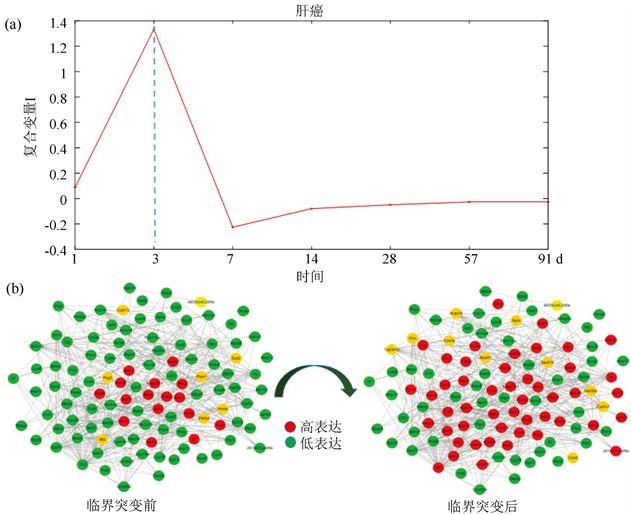
Figure 5. The line chart of early-warning signals and the overturn network during the progression of liver cancer
图5. 肝癌临界信号折线图以及翻转网络图
基金项目
广州市科技计划珠江科技新星专项项目资助(No. 201610010029)。
文章引用
关小玲. 基于个体时序列差异网络探测疾病恶化的预警信号
Detecting the Early Warning Signals of Disease Progression Based on Individual Difference Time Series Network[J]. 应用数学进展, 2019, 08(01): 160-169. https://doi.org/10.12677/AAM.2019.81018
参考文献
- 1. Liu, X., Wang, Y., Ji, H., et al. (2016) Personalized Characterization of Diseases Using Sample-Specific Networks. Nucleic Acids Research, 44, e164. https://doi.org/10.1093/nar/gkw772
- 2. Pei, C., Yongjun, Li., Liu, X., Liu, R. and Luonan, C. (2017) Detecting the Tipping Points in a Three-State Model of Complex Diseases by Temporal Dif-ferential Networks. Journal of Translational Medicine, 15, 217. https://doi.org/10.1186/s12967-017-1320-7
- 3. Liu, R., et al. (2012) Identifying Critical Transitions and Their Leading Biomolecular Networks in Complex Diseases. Scientific Reports, 2, 813. https://doi.org/10.1038/srep00813
- 4. Liu, R., Yu, X., Liu, X., Xu, D., Aihara, K. and Chen, L. (2014) Identifying Critical Transitions of Complex Diseases Based on a Single Sample. Bioinformatics, 30, 1579-1586. https://doi.org/10.1093/bioinformatics/btu084
- 5. Chen, P. and Li, Y. (2016) The Decrease of Consistence Probability: At the Crossroad of Catastrophic Transition of a Biological System. BMC Systems Biology, 10, 50. https://doi.org/10.1186/s12918-016-0295-y
- 6. Liu, X.P., Liu, Z.-P., Zhao, X.-M. and Chen, L.N. (2012) Iden-tifying Disease Genes and Module Biomarkers by Differential Interactions. Journal of the American Medical Informatics Association, 19, 241-248. https://doi.org/10.1136/amiajnl-2011-000658
- 7. Chen, L., Liu, R., Liu, Z., Li, M. and Aihara, K. (2012) De-tecting Early-Warning Signals for Sudden Deterioration of Complex Diseases by Dynamical Network Biomarkers. Scientific Reports, 2, 342. https://doi.org/10.1038/srep00342
- 8. Louro, R., Nakaya, H.I., Amaral, P.P., et al. (2007) Androgen Responsive Intronic Non-Coding RNAs. BMC Biology, 5, 4. https://doi.org/10.1186/1741-7007-5-4
- 9. Lempiäinen, H., Couttet, P., Bolognani, F., et al. (2013) Identification of Dlk1-Dio3 Imprinted Gene Cluster Noncoding RNAs as Novel Candidate Biomarkers for Liver Tumor Promotion. Toxicological Sciences, 131, 375-386. https://doi.org/10.1093/toxsci/kfs303