Advances in Applied Mathematics
Vol.
08
No.
02
(
2019
), Article ID:
29025
,
7
pages
10.12677/AAM.2019.82036
The Generalized 3-Connectivity of Cartesian Product of Complete Graphs
Hengzhe Li, Yuanyuan Lu, Jiajia Wang
College of Mathematics and Information Science, Henan Normal University, Xinxiang Henan

Received: Feb. 3rd, 2019; accepted: Feb. 18th, 2019; published: Feb. 26th, 2019

ABSTRACT
Let S be a set of at least two vertices in a graph G. A subtree T of G is an S-Steiner tree if . Two S-Steiner trees and are internally disjoint if and . Let be the maximum number of internally disjoint S-Steiner trees in G, and let be the minimum for S ranges over all k-subsets of . In this paper, we study the -connectivity of Cartesian product of complete graphs, determine for any two complete graphs; for any k complete graphs, where .
Keywords:Complete Graphs, -Connectivity, Cartesian Product

完全图的笛卡尔积的广义3-连通度
李恒哲,芦园园,王佳佳
河南师范大学数学和信息科学学院,河南 新乡

收稿日期:2019年2月3日;录用日期:2019年2月18日;发布日期:2019年2月26日

摘 要
设S是图G中至少有2个顶点的集合,T是G的一棵子树。如果 ,则称T是G的一棵S-斯坦纳树。设 与 是S-斯坦纳树,如果 且 ,则称 与 是内部不交的S-斯坦纳树。 表示图G中内部不交的S-斯坦纳树的最大数目, 是当S遍及 的所有k元子集时的最小的 。在本文中,我们研究完全图的笛卡尔积的 -连通度。对于任意两个完全图 与 ,确定 ;对于任意 个完全图,确定 。
关键词 :完全图, -连通度,笛卡尔积

Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在本文中,所有的图都是无向、有限的简单图。对于在本文中没有提到的图论的概念与术语,我们可以参考 [1] 。
设图G是一个连通图,S是图G中至少有2个顶点的集合,T是G的一棵子树。如果 ,则称T是G的一棵S-斯坦纳树。设 与 是S-斯坦纳树,如果 且 ,则称 与 是内部不交的S-斯坦纳树。对于 的一个子集S, 表示图G中内部不交的S-斯坦纳树的最大数目。如果 ,则 是局部点连通度。对于 的整数, 是当S遍及 的所有k元子集时的最小的 ,称它为广义k-连通度,简称 -连通度。Chartrand等人 [2] 引入了 -连通度。显然,当 时, 。
笛卡尔积是最重要的图运算之一,并且在网络的设计与分析中有重要作用。在过去的几十年,许多图论学者研究了笛卡尔积图的(边)连通度 [3] - [9] 。显然,在同构意义下,该运算满足交换律,即 ,该运算满足结合律,即 。
对于一般图G来说,确定 是一件非常困难的事情。到目前为止,只有少数图类的 -连通度被确定,例如,Chartrand等人 [10] 确定了完全图的 -连通度;Lin和Zhang确定了超立方体的 -连通度;Li和Wang [11] 确定了递归循环图的 -连通度与 -连通度,等等。图论学者研究了图的广义连通度的上界与下界 [12] [13] [14] [15] [16] ,图论学者研究了图运算的广义(边)连通度的上界与下界 [12] [17] 。更多的结果,可以参考 [18] 。
在本文中,我们将研究完全图的笛卡尔积的 -连通度。本文的结构如下,在第2部分,我们将介绍一些定义和已知的结论;在第3部分,我们将给出主要的结果。
2. 预备知识
设G和H是两个图,图G与H的笛卡尔积,记作 ,其顶点集为 ,两个顶点 与 相邻当且仅当 且 ,或 且 。特别地,n条路的笛卡尔积是n-维网格图。长为1的n条路的笛卡尔积是n-维超立方体。
设G与H是两个图,顶点集分别为 , 。我们用 来表示 的子图,这个子图是由顶点集 诱导出来的。类似的,我们用 来表示 的子图,这个子图是由顶点集 诱导出来的。显然,对于图G中的不同顶点 与 ,有 。为了简单,我们可以用 来代替 。类似的,我们也可以用 来代替 。下面的几个符号可以简化我们的证明。
给定一个顶点 ,对于 中的任意顶点u,有 ,对于G中的任意子图 ,有 ,其中 , 。
给定一个顶点 ,对于任意顶点 ,有 ,对于任意子图 ,有 ,其中 , 。
类似的,给定一个顶点 ,对于 可以定义映射 ,对于 可以定义映射 ;给定一个顶点 ,对于 可以定义映射 ,对于 可以定义映射 。
下面的几个定理和引理对我们要证明的结果很重要。
定理2.1 [10] :对于任意两个整数n和k, ,有 。
引理2.2 [13] :设图G是一个至少有3个顶点的连通图,如果图G有两个最小度为 的相邻顶点,则有 ;而且,上界是紧的。
定理2.3 [1] :设图G是一个k-连通图,如果x与y是G中的一对不同顶点,那么在图G中存在k条内部不交的xy-路 。
引理2.4 [19] :如果图G是k-连通的,那么对于任意顶点x和子集 ,满足 ,都有一个大小为k的x,U-扇。
定理2.5 [20] : , 。
引理2.6 [20] :设 是两个整数, ,G是一个r-正则图,如果 ,那么 。
引理2.7 [17] :设 是k个圈,则 。
3. 主要定理及其证明
在本文中, 表示有 个顶点的完全图,其中 。一条xy-路是一条起始于x,终止于y的路。对于一条路P来说,其中 ,我们用 去表示P上连接 的子路。
定理3.1:对于任意两个完全图 与 ,有 。
证明:根据 与 的取值情况,考虑如下三种情形。
情形1: 。
因为 ,所以两个完全图都是 。显然, 。
情形2: 。
由引理2.2知, ,故只需证 。令 , , 。下面分两种子情形讨论。
子情形2.1: , 。
不失一般性,假设 。由定理2.1知, ,故在 中有 棵内部不交的S-斯坦纳树,记作 。令 。显然, 是 棵内部不交的S-斯坦纳树。
子情形2.2:S中的某两个顶点属于某个 , 。
不失一般性,假设
,
。因为
,
,
,所以由定理2.3知,在
中存在
条内部不交的xy-路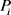 ,
,在
中存在
条内部不交的
-路
,
。令
是在
上的x的邻点。令
,
。显然,
是
棵内部不交的S-斯坦纳树。
,
,在
中存在
条内部不交的
-路
,
。令
是在
上的x的邻点。令
,
。显然,
是
棵内部不交的S-斯坦纳树。
情形3: 。
由引理2.2知, ,故只需证 。令 , , 。下面分三种子情形讨论。
子情形3.1: , 。
因为此情形与子情形2.1的讨论类似,所以留给读者证明。
子情形3.2:S中的某两个顶点属于某个 , 。
因为此情形与子情形2.2的讨论类似,所以留给读者证明。
子情形3.3:S中的三个顶点分别属于不同的 , 。
不失一般性,设 , , 。下面分三种情形讨论。
如果 ,不妨设 。由定理2.1知, ,所以在 中有 棵内部不交的S-斯坦纳树,记作 。令 , 。显然, 是 棵内部不交的S-斯坦纳树。
如果 , , 其中 。因为 , ,所以由定理2.3知,在 中存在 条内部不交的 -路 , 。因为 是简单图,所以在 中可以找到 条长度至少为2的 -路 , 。令 是在 上的x的邻点, , ; ; ; , 。显然, 是 棵内部不交的S-斯坦纳树。
如果 , , ,其中 不相等。当 时,由引理2.7知, ,故定理成立。当 和 时,令 是在图 中除顶点 与 外的x的邻点,则 , 。令 ; ; ; , 。显然, 是 棵内部不交的S-斯坦纳树。
定理3.2:对于任意 个完全图,有 。
证明:对k用归纳法。因为图的笛卡尔积满足交换律和结合律,所以可设 。如果 ,那么 是超立方体 ,由定理2.5与引理2.6知,定理成立。
接下来只讨论 即可。当 时,由定理3.1知,定理成立;假设对于任意不超过 个完全图的笛卡尔积,定理都成立,即 成立;现在证明对于任意k个完全图的笛卡尔积,定理成立。由引理2.2知, ,故只需证 。为了简便,令图G表示图 , , 。令 , , 。考虑如下三种情形。
情形1: , 。
不失一般性,假设 。由归纳假设知,在 中可以找到a棵内部不交的S-斯坦纳树,记作 。我们只需在 外找 棵内部不交的S-斯坦纳树,令 , 。显然, 是b棵内部不交的S-斯坦纳树。
情形2:S中的某两个顶点属于某个 , 。
不失一般性,假设 , 。下面分两种子情形讨论。
子情形2.1: 。
因为 , , ,所以由定理2.3知,在 中存在 条内部不交的xy-路 , ,在 中存在 条内部不交的 -路 , 。令 是在 上的x的邻点。在 中任取一棵 -斯坦纳树 , 。令 , ; , 。显然, 是b棵内部不交的S-斯坦纳树。
子情形2.2: 。
不失一般性,假设
。因为
,
,所以由定理2.3知,在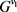 中存在
条内部不交的xy-路
,
。令
是在
上的x的邻点。令
,
;
,
。显然,
是b棵内部不交的S-斯坦纳树。
中存在
条内部不交的xy-路
,
。令
是在
上的x的邻点。令
,
;
,
。显然,
是b棵内部不交的S-斯坦纳树。
情形3:S中的三个顶点分别属于不同的 , 。
不失一般性,假设 , , 。下面分三种子情形讨论。
子情形3.1: , 。
不失一般性,假设 。因为 ,所以在 中,顶点x有 个邻点,记作 。令 , 。又因为 是完全图,所以由定理2.1知, ,故在 中有 棵内部不交的S-斯坦纳树,记作 。显然, 是b棵内部不交的S-斯坦纳树。
子情形3.2: , , 。
因为 , ,所以由定理2.3知,在 中存在 条内部不交的 -路 , 。因为图G是简单图,所以在 中可以找到a条长度至少为2的 -路 , 。令 是在 上的x的邻点。令 , ; ; ; , 。显然, 是b棵内部不交的S-斯坦纳树。
子情形3.3: , , ,其中 不相等。
令 , 。考虑如下两种情况。
如果在G中, 中的某两个顶点不相邻。不失一般性,假设在G中 不相邻。因为 ,所以在G中存在 条内部不交的 -路,记作 ,设 是 的邻点, 。假设 不在 上, 。由引理2.4知,在G中存在一个从 到 的 -扇,记作 ,其中有一条 -路, , 是一条 -路。令 , 。因为每个 有一棵支撑树 , ,所以我们找到a棵内部不交的S-斯坦纳树,记作 。因为 是 -连通的,所以在 中存在 条内部不交的 -路,记作 ,设 是 的邻点, 。又因为 是完全图,所以可假设 ,令 , ,故 , 。
因为 ,所以在 中存在一个从 到 的 -扇,记作 ,其中有一条 -路, ,有一条 -路 。令 , ; ; 。显然, 是b棵内部不交的S-斯坦纳树(如图1所示)。

Figure 1. Solid lines in bold for , ; Solid lines for , ; Dashed lines for ; Dashed lines in bold for
图1. 粗实线表示 , ;细实线表示 , ;细虚线表示 ;粗虚线表示
如果在G中, 两两相邻。由引理2.7知,在 中有3条内部不交的S-斯坦纳树,记作 。因为G是 -连通的,所以 ,故在 中存在 条内部不交的 -路,记作 。令 是 的邻点, 。由引理2.4知,在 中存在一个从 到 的 -扇。类似于情况1,可以构造 棵内部不交的S-斯坦纳树 。又因为 ,所以可以构造 棵内部不交的S-斯坦纳树 。显然, 是b棵内部不交的S-斯坦纳树。
基金项目
国家自然科学基金(No. 11401181)。
致谢
作者非常感谢审稿人和编辑的宝贵意见和建议,改善了本文的呈现。
文章引用
李恒哲,芦园园,王佳佳. 完全图的笛卡尔积的广义3-连通度
The Generalized 3-Connectivity of Cartesian Product of Complete Graphs[J]. 应用数学进展, 2019, 08(02): 320-326. https://doi.org/10.12677/AAM.2019.82036
参考文献
- 1. Bondy, J.A. and Murty, U.S.R. (2008) Graph Theory, GTM 244. Springer, Berlin.
- 2. Chartrand, G., Kapoor, S.F., Lesniak, L. and Lick, D.R. (1984) Generalized Connectivity in Graphs. Bulletin of the Bombay Mathematical Colloquium, 2, 1-6.
- 3. Chiue, W.-S. and Shieh, B.-S. (1999) On Connectivity of Cartesian Product of Two Graphs. Applied Mathematics and Computation, 102, 129-137. https://doi.org/10.1016/S0096-3003(98)10041-3
- 4. Imrich, W. and Klavžar, S. (2000) Product Graphs. Structure and Recognition. Wiley-Interscience Series in Discrete Mathematics and Optimization, Wiley, New York.
- 5. Imrich, W., Klavžar, S. and Rall, D.F. (2008) Topics in Graph Theory. Graphs and Their Cartesian Product. AK Peters, Wellesley.
- 6. Klavžar, S. and Spacapan, S. (2008) On the Edge-Connectivity of Cartesian Product Graphs. Asian-European Journal of Mathematics, 1, 93-98.
- 7. Sabidussi, G. (1957) Graphs with Given Group and Given Graph-Theoretic Properties. Canadian Journal of Mathematics, 9, 515-525. https://doi.org/10.4153/CJM-1957-060-7
- 8. Špacapan, S. (2008) Connectivity of Cartesian Products of Graphs. Applied Mathematics Letters, 21, 682-685. https://doi.org/10.1016/j.aml.2007.06.010
- 9. Xu, J. and Yang, C. (2006) Connectivity of Cartesian Product Graphs. Discrete Mathematics, 306, 159-165. https://doi.org/10.1016/j.disc.2005.11.010
- 10. Chartrand, G., Okamoto, F. and Zhang, P. (2010) Rainbow Trees in Graphs and Generalized Connectivity. Networks, 55, 360-367.
- 11. Li, H. and Wang, J. (2018) The λ3-Connectivity and κ3-Connectivity of Recursive Circulants. Applied Mathematics and Computation, 339, 750-757. https://doi.org/10.1016/j.amc.2018.07.065
- 12. Li, H., Li, X. and Sun, Y. (2012) The Generalied 3-Connectivity of Cartesian Product Graphs. Discrete Mathematics and Theoretical Computer Science, 14, 43-54.
- 13. Li, S., Li, X. and Zhou, W. (2010) Sharp Bounds for the Generalized Connectivity κ3(G). Discrete Mathematics, 310, 2147-2163. https://doi.org/10.1016/j.disc.2010.04.011
- 14. Li, X. and Mao, Y. (2014) The Generalized 3-Connectivity of Lexicographic Product Graphs. Discrete Mathematics and Theoretical Computer Science, 16, 339-354.
- 15. Li, X., Mao, Y. and Sun, Y. (2014) On the Generalized (Edge-)Connectivity of Graphs. Australasian Journal of Combinatorics, 58, 304-319.
- 16. Li, H., Wu, B., Meng, J. and Ma, Y. (2018) Steiner Tree Packing Number and Tree Connectivity. Discrete Mathematics, 341, 1945-1951. https://doi.org/10.1016/j.disc.2018.03.021
- 17. Li, H., Ma, Y., Yang, W. and Wang, Y. (2017) The Generalized 3-Connectivity of Graph Products. Applied Mathematics and Computation, 295, 77-83. https://doi.org/10.1016/j.amc.2016.10.002
- 18. Li, X. and Mao, Y. (2016) Generalized Connectivity of Graphs. In: Springer Briefs in Math, Springer, New York. https://doi.org/10.1007/978-3-319-33828-6
- 19. Dirac, G.A. (1960) In abstrakten graphen vorhandene voll-standige 4-graphen und ihre unterteilungen. Mathematische Nachrichten, 22, 61-85. https://doi.org/10.1002/mana.19600220107
- 20. Lin, S. and Zhang, Q. (2017) The Generalized 4-Connectivity of Hypercubes. Discrete Applied Mathematics, 220, 60-67. https://doi.org/10.1016/j.dam.2016.12.003