Advances in Applied Mathematics
Vol.
08
No.
03
(
2019
), Article ID:
29321
,
9
pages
10.12677/AAM.2019.83059
The Linear Bayesian Estimation of Parameters in Seemingly Unrelated Model Based on Covariance Autoregressive Matrix
Xiaoling Ma*, Xijian Hu#
College of Mathematics and System Sciences, Xinjiang University, Urumqi Xinjiang

Received: Mar. 1st, 2019; accepted: Mar. 13th, 2019; published: Mar. 20th, 2019

ABSTRACT
In this paper, we propose a mean-covariance seemingly uncorrelated model with known covariance structures. The mean-covariance model is used to describe the autoregressive model with time correlation, and the parameters of this model were estimated by using linear Bayesian estimate. Under the criterion of mean square error matrix, the generalized least squares estimation method and the linear Bayes estimation method were compared; with respect to the generalized least squares estimation method, the superiority of Bayes Linear Estimator is verified by simulation.
Keywords:Seemingly Uncorrelated Model, Autoregressive Model, Linear Bayesian Estimation Method, Mean Square Error Criterion
基于自回归协方差阵的似乎不相关模型参数的线性贝叶斯估计
马晓玲*,胡锡健#
新疆大学数学与系统科学学院,新疆 乌鲁木齐

收稿日期:2019年3月1日;录用日期:2019年3月13日;发布日期:2019年3月20日

摘 要
在本文中,构造了已知协方差矩阵结构的均值–协方差似乎不相关模型,该均值–协方差模型考虑了具有时间相关性的自回归模型,并得到该模型参数的线性Bayes估计。在均方误差矩阵准则下对与广义最小二乘估计方法和线性Bayes估计方法进行了对比,通过模拟验证了相对于广义最小二乘估计方法的优良性。
关键词 :似乎不相关模型,自回归模型,线性Bayes估计方法,均方误差准则

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
Zellner [1] [2] 首次提出了似乎不相关模型(seemingly unrelated regression,简称SUR);一般研究不同区域或不同因素之间的相关关系,通过随即扰动项相互关联建立这种相关关系,在实际生活中,纵向数据有时也存在着某种相关联系,因此我们研究具有时间异质性的似乎不相关模型。线性贝叶斯方法最早是由Rao [3] [4] 提出的,主要是在参数的线性类中利用最优化方法选取能使线性估计Bayes风险达到最小的一种方法,该方法假定参数的先验分布的二阶矩存在;Gruber [5] 研究了线性回归模型中可估参数的线性Bayes估计;张伟平等人 [6] 研究了多元线性模型的线性贝叶斯无偏估计的优越性;李胜宏等人 [7] 在给定的先验信息条件下得到了似乎不相关模型的参数Bayes估计,并在均方误差和PC准则下,比较了线性贝叶斯估计与最小二乘估计的优良性;宋慧明 [8] 讨论了半相依回归模型参数的Bayes线性无偏估计及与广义最小二乘估计方法相比较的优良性。
在纵向数据的研究中,群集数据的一个特征是其数据之间是相关的。魏凤荣 [9] 曾将均值协方差模型与似乎不相关模型相结合,讨论了其极大似然估计方法;对于协方差矩阵模型的研究中,有些学者引入
了自回归模型 [10] ,其表现形式 。
本文将具有时间相关性的似乎不相关模型与自回归模型相结合,利用线性Bayes估计方法对参数进行估计。
2. 模型介绍
(1)
其中i表示第i个时期, 是 维的被解释列向量, 是已知的 的解释变量矩阵,且是列满秩的,即 ; 是 维的未知回归系数向量; 是 维随机扰动的列向量,并假定随机扰动项的均值为0,其协方差阵是均值协方差阵 是未知的。并假设 是相互独立的。为方便起见, 是对称正定矩阵。令 ,
用矩阵表示(1)式为:
即
(2)
3. 三个时期似乎不相关模型参数的线性贝叶斯估计
由模型(2)可知回归系数的广义最小二乘估计为:
(3)
为求(2)式参数的线性贝叶斯估计,假设参数 的先验分布为 ,并满足条件:
(4)
其中 , , 均已知。
假设所求的参数 的线性贝叶斯估计是在以下线性类中产生的最优:
并选取损失函数:
相对应的风险函数为:
定理1. 在Gauss-Markov条件下,设待估参数的先验分布的二阶矩存在且是无偏估计,其风险函数在某线性类中可以找到最优解,则该参数的线性Bayes估计为:
其中 是广义最小二乘估计式, 的表现形式如(4)式。
证明:
由 的无偏性可知
为求最小的C矩阵,让其风险函数达到最小,即
令
有
由矩阵公式:
从而有
又因为
所以有:
(5)
下证无偏性:
由广义最小二乘估计的无偏性知 所以有
4. 线性贝叶斯估计的优良性
均方误差矩阵下的线性Bayes估计的优良性
定义4.1设参数向量 的一个估计量为 ,则 的均方误差定义为:
,而 称为 的均方误差矩阵。设 是参数向量 的两个不同的估计,如果 或 ,则称 在MSEM准则(或MSE准则)下优于 。
显然,MSEM准则比MSE准则的判别效果要强,一个估计量在MSEM准则下优于另一个估计量,则在MSE准则下也成立,反之不然。
定理2: 、 分别表示参数 的广义最小二乘估计和线性贝叶斯估计,且分别满足(3)式和(5)式,则有:
证明:由(5)式和均方误差矩阵定义可知
其中:
(7)
(8)
将(8)式代入(7)式得:
(9)
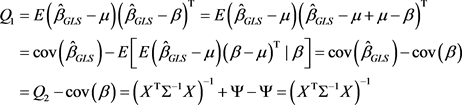 (10)
(10)
将(9)、(10)式带入(6)式得:
所以
其中 是对称正定矩阵。
5. 模拟实验
5.1. 实验设计
取模拟试验方程组为表示不同时期即 的三个时间异质性问题的似乎不相关模型,每个时期的参数个数为 ,其中包含常系数,三个时期参数总个数为 ,其中自变量的观测值 都是 维的矩阵并分别取自不同的分布: ,且每个自变量都是列满秩矩阵即 。
对广义最小二乘估计方法设定参数 初值:
随即扰动项 满足特殊的均值——协方差矩阵 。其中k,l表示时期。
在模拟中分别取各个时期的相关关系 为0.2,0.4,0.6,0.8。并令 ,用线性Bayes估计方法对参数 估计时须设定参数的先验信息,我们假定参数 的均值与协方差矩阵分别为:
、
由于线性Bayes的估计方法依赖于先验信息的设定,在此假定每个时期的各参数均值与真实值相同,然后分别用广义最小二乘估计方法与线性Bayes估计方法得到 的估计值。
5.2. 拟合效果的评价指标
分别选取绝对偏差的均值和均方误差均值作为拟合效果的评价指标。重复试验下的N个参数估计值的平均值为:
绝对偏差表示为: ,
绝对偏差的均值表示为: 。
在N次重复试验下,系数估计值的均方误差为:
当 和 的值越小时,说明系数函数估计的精确度越高。
表示广义最小二乘估计, 表示线性Bayes估计。
5.3. 实验结果及分析
为了更全面的考察线性Bayes估计的有效性,重复试验 次,分别计算广义最小二乘方法和线性Bayes估计方法下的 和 的值,在给定广义最小二乘均值及线性Bayes均值条件下,
我们分别得到在已知相关系数 情况下参数广义最小二乘估计值及线性Bayes估计值,为了方便比较,把各模拟结果列表如表1:
Table 1. The estimates of two estimates and their means of absolute deviation
表1. 两种估计的估计值及其绝对偏差均值
从表中我们可以看出,两种估计方法的估计值都比较接近初值的设定,但线性Bayes估计方法的绝对偏差均值和均方误差都小于广义最小二乘估计方法所计算的结果,说明线性Bayes估计方法的估计结果更精确。
相关系数 的变化范围在(−1,1)之间,在模拟过程中给 取了几个特殊值,我们不难从表中发现,随着 的增大,两种方法的估计值越接近真实值,并且两个方法的绝对偏差均值和均方误差都是逐渐缩小,说明不同时期之间是存在着相关性的,且具有较强的相关性。
6. 结论
本文在 已知的情况下,通过用线性Bayes估计方法和广义最小二乘估计方法得到三个时期含有不同维度的自变量的估计表达式,并用均方误差矩阵准则得到线性Bayes估计方法的优良性;随后在模拟
过程中通过 和 两个指标作为两种估计方法的拟合指标,分析出线性Bayes估计方法比
广义最小二乘估计方法拟合效果好。
文章引用
马晓玲,胡锡健. 基于自回归协方差阵的似乎不相关模型参数的线性贝叶斯估计
The Linear Bayesian Estimation of Parameters in Seemingly Unrelated Model Based on Covariance Autoregressive Matrix[J]. 应用数学进展, 2019, 08(03): 531-539. https://doi.org/10.12677/AAM.2019.83059
参考文献
- 1. Zellner, A. (1962) An Efficient Method of Estimating Seemingly Unrelated Regressions and Tests for Aggregation Bias. Publications of the American Statistical Association, 57, 348-368. https://doi.org/10.1080/01621459.1962.10480664
- 2. Zellner, A. (1963) Estimators for Seemingly Unrelated Regression Equations: Some Exact Finite Sample Results. Publications of the American Statistical Association, 58, 977-992. https://doi.org/10.1080/01621459.1963.10480681
- 3. Rao, C.R. (1973) Linear Statistical Inference and Its Applications. 2nd Edition, Wiley, New York. https://doi.org/10.1002/9780470316436
- 4. Rao, C.R. (1980) Some Comments on the Minimum Mean Square Error as a Criterion of Estimation. Statistics & Related Topics, Ottawa, 5-8 May 1980, 123-143. https://doi.org/10.21236/ADA093824
- 5. Gruber, M.H.J. (1990) Regression Estimators, A Comparative Study. Academic Press, Boston.
- 6. Zhang, W.-P., Wei, L.-S. and Chen, Y. (2012) The Superiorities of Bayes Linear Un-biased Estimator in Multivariate Linear Models. Acta Mathematicae Applicatae Sinica (English Series), 28, 383-394. https://doi.org/10.1007/s10255-012-0150-x
- 7. 李胜宏, 周占功. 相依回归系统参数的Bayes估计[J]. 江苏科技大学学报(自然科学版), 2006, 20(5): 32-36.
- 8. 宋慧明. 半相依回归模型参数的Bayes估计[D]: [硕士学位论文]. 合肥: 中国科学技术大学, 2006.
- 9. 魏凤荣. 似乎不相关回归方程组中参数的极大似然估计[J]. 系统工程理论与实践, 1999, 19(2): 62-64.
- 10. Littell, R.C., Pendergast, J. and Natarajan, R. (2000) Modelling Covariance Structure in the Analysis of Repeated Measures Data. Statistics in Medicine, 19, 1793-1819. 3.0.CO;2-Q>https://doi.org/10.1002/1097-0258(20000715)19:13<1793::AID-SIM482>3.0.CO;2-Q
NOTES
*第一作者。
#通讯作者。
