Advances in Applied Mathematics
Vol.
09
No.
03
(
2020
), Article ID:
34689
,
6
pages
10.12677/AAM.2020.93049
Multiple Online List Coloring
Jiayan Yan
College of Mathematics and Computer Science, Zhejiang Normal University, Jinhua Zhejiang

Received: Mar. 1st, 2020; accepted: Mar. 16th, 2020; published: Mar. 24th, 2020

ABSTRACT
In online list coloring (introduced by Zhu and by Schauz in 2009), the list configuration of the graph is given online as the online coloring game proceeds. James Carraher, Sarah Loeb and Thomas Mahoney etc. proved a partial result toward the paint analogue of Ohba's Conjecture. We extend this result to multiple online coloring.
Keywords:Multiple Online List Coloring, Ohba’s Conjecture

多重在线列表染色
颜嘉燕
浙江师范大学数学与计算机科学学院,浙江 金华

收稿日期:2020年3月1日;录用日期:2020年3月16日;发布日期:2020年3月24日

摘 要
在2009年Zhu和Schauz分别提出的在线列表染色中,图的列表配置是随着在线染色游戏的进行在线给出的。James Carraher,Sarah Loeb和Thomas Mahoney等人证明了在线版本的Ohba猜想的一部分。我们将这个结果推广到了多重染色中。
关键词 :多重在线列表染色,Ohba猜想

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
设G是一个图,f和g是由 映射到
映射到 的两个函数,其中对G中的任意一点v都满足
的两个函数,其中对G中的任意一点v都满足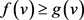 。G的一个f-列表配置是一个映射L,分配给G中的每一点v一个由
。G的一个f-列表配置是一个映射L,分配给G中的每一点v一个由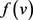 个正整数组成的集合
个正整数组成的集合 作为点v可以用的颜色。G的一个g-染色是一个映射S,分配给G中的每一点v一个由
作为点v可以用的颜色。G的一个g-染色是一个映射S,分配给G中的每一点v一个由 个颜色组成的集合
个颜色组成的集合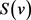 ,使得对G中任意相邻的两点u和v都满足
,使得对G中任意相邻的两点u和v都满足 。对于G的一个列表配置L,G的一个
。对于G的一个列表配置L,G的一个 -染色是G的一个g-染色,且对于G中每个点v都满足
-染色是G的一个g-染色,且对于G中每个点v都满足 。如果G有一个
。如果G有一个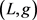 -染色,就称G是
-染色,就称G是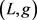 -可染的。称G是
-可染的。称G是 -可选当且仅当G对于任意f-列表配置L,都是
-可选当且仅当G对于任意f-列表配置L,都是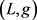 -可染的。根据定义,我们可以得到如下结论:
-可染的。根据定义,我们可以得到如下结论:
• 如果 ,其中b是一个常数,则
,其中b是一个常数,则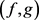 -可选就是
-可选就是 -可选。
-可选。
• 如果 ,则
,则 -可选就是f-可选。
-可选就是f-可选。
• 如果 ,其中a和b都是常数,则
,其中a和b都是常数,则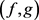 -可选就是
-可选就是 -可选。
-可选。
列表染色已经有了很多广泛的研究。一般,我们称最小的使得G是k-可选的正整数k为图G的选择数,用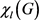 表示。
表示。
在本文中,我们还考虑了列表染色的另一个版本。在2009年,Zhu和Schauz [1] 介绍了由列表染色推广而来的一种染色,称为在线列表染色。在线列表染色的定义可以通过一个双人游戏来表示。
定义1:设G是一个图,f和g是两个映射 ,G的
,G的 -列表染色游戏由两个玩家组成,分别叫Lister和Painter。游戏的开始,G中的每个点v都有
-列表染色游戏由两个玩家组成,分别叫Lister和Painter。游戏的开始,G中的每个点v都有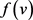 个筹码。在游戏的每一轮i:
个筹码。在游戏的每一轮i:
Lister先从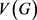 中还没有染到
中还没有染到 个颜色的点中选一个非空子集
个颜色的点中选一个非空子集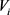 ,同时,
,同时, 中的每个点都将减少一个筹码;而玩家Painter将从
中的每个点都将减少一个筹码;而玩家Painter将从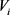 中选择一个独立集
中选择一个独立集 ,给
,给 中每个点染颜色i。
中每个点染颜色i。
如果存在某个正整数m使得在游戏的第m步时,有一个点v已经没有筹码了并且这个点还没有被染到 个颜色,那么Lister赢了。
个颜色,那么Lister赢了。
否则,也就是在某一步,每个点v都已经被染了 个颜色。这个情况,我们就称Painter赢了游戏。
个颜色。这个情况,我们就称Painter赢了游戏。
如果Painter在 -列表染色游戏中有一个赢的策略,那么我们就称G是在线
-列表染色游戏中有一个赢的策略,那么我们就称G是在线 -可选的。当f和g是两个常数函数
-可选的。当f和g是两个常数函数 时,称G是在线
时,称G是在线 -可选的。如果
-可选的。如果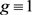 ,则在线
,则在线 -可选就是在线f-可选。
-可选就是在线f-可选。
我们称最小的使得G是在线k-可选的正整数k为图G的在线选择数,用 表示。根据定义我们可以知道对于所有图G,都有
表示。根据定义我们可以知道对于所有图G,都有 且
且 。
。
Ohba [2] 在2002年提出了一个猜想,一个图G如果满足 ,则这个图就满足
,则这个图就满足 。这个猜想已经被Noel,Reed和Wu [3] 证明了是正确的。
。这个猜想已经被Noel,Reed和Wu [3] 证明了是正确的。
定理1:如果图G满足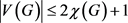 ,则
,则 。
。
而关于在线选择数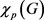 ,也有一个类似的猜想。
,也有一个类似的猜想。
猜想1:如果图G满足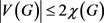 ,则
,则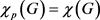 。
。
尽管已经有一些结果证明了存在图G满足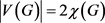 是在线选择数等于选择数的,但是在线版本的Ohba猜想目前还没有被证明。关于在线版本的Ohba猜想的一个弱一点的版本的猜想是存在常数
是在线选择数等于选择数的,但是在线版本的Ohba猜想目前还没有被证明。关于在线版本的Ohba猜想的一个弱一点的版本的猜想是存在常数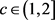 使得当
使得当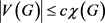 时,
时,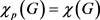 。Kozik,Micek和Zhu [4] 证明了如果
。Kozik,Micek和Zhu [4] 证明了如果 ,则
,则 。Carraher,Loeb和Mahoney [5] 证明了如果
。Carraher,Loeb和Mahoney [5] 证明了如果 ,则
,则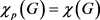 。
。
定理2:如果 ,则
,则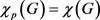 。
。
定理3:如果 ,则
,则 。
。
定理4:设G是一个独立数为m的图,且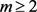 ,若
,若

则 。
。
Erdös,Rubin和Taylor提出了猜想如果G是k-可选的,则G对于任意正整数m是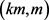 -可选的。然而,Zdenĕk Dvořák,Xiaolan Hu和Jean-Sébastien Sereni [6] 证明了若
-可选的。然而,Zdenĕk Dvořák,Xiaolan Hu和Jean-Sébastien Sereni [6] 证明了若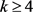 ,存在图G是k-可选的,但不是
,存在图G是k-可选的,但不是 -可选的。但是这个图是不满足Ohba猜想的条件的,因此我们可以思考,在Ohba猜想的条件下,Erdös猜想是否成立。也就是,当
-可选的。但是这个图是不满足Ohba猜想的条件的,因此我们可以思考,在Ohba猜想的条件下,Erdös猜想是否成立。也就是,当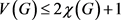 ,如果
,如果 ,G是否对于任意正整数m都是是
,G是否对于任意正整数m都是是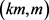 -可选的。
-可选的。
问题1:设G是一个简单图且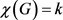 ,如果
,如果 ,G是否对于任意正整数m都是
,G是否对于任意正整数m都是 -可选的?
-可选的?
根据在线列表染色的定义,我们可以知道如果G对任意正整数m都是在线 -可选的,则G对任意正整数m都是在线
-可选的,则G对任意正整数m都是在线 可选的。
可选的。
因此对于在线列表染色,我们有类似的问题。
问题2:设G是一个简单图且 ,如果
,如果 ,G是否对于任意正整数m都是在线
,G是否对于任意正整数m都是在线 -可选的?
-可选的?
然而,在线版本的Ohba猜想目前还没有被证明,因此我们在弱Ohba猜想的结果上进行了推广,证明了如果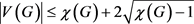 ,则G是否对于任意正整数m都是在线
,则G是否对于任意正整数m都是在线 -可选的。
-可选的。
2. 主要定理证明
在这个部分,我们将证明如果对任意正整数m,图G都是在线 列表可选的,那么我们可以通过加上一个点数有限制的独立集来构造一个对于任意正整数m都是在线
列表可选的,那么我们可以通过加上一个点数有限制的独立集来构造一个对于任意正整数m都是在线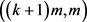 -列表可选的图。
-列表可选的图。
在此之前,我们先介绍一些证明中将用到的表示方法。对于图G和图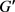 ,将通过加上图G的点与图
,将通过加上图G的点与图 的点之间的所有的边联合所获得图称为图G和图
的点之间的所有的边联合所获得图称为图G和图 的结合,用
的结合,用 表示。对于图G的任意一点v,令
表示。对于图G的任意一点v,令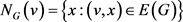 ,
, 。
。
在证明主要定理之前,先介绍多重在线列表染色的一个重要性质。
定理5:对于图G中的一点v,如果 ,则G是在线
,则G是在线 -列表可选的等价于
-列表可选的等价于 是在线
是在线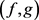 -列表可选的。
-列表可选的。
我们称多重在线列表染色的这个性质为退化。利用这个性质,我们希望能由一个对任意正整数m都是在线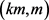 -列表可选的图构造出一个对任意正整数m都是在线
-列表可选的图构造出一个对任意正整数m都是在线 -列表可选的图。
-列表可选的图。
当我们描述两个玩家的策略的时候,称Lister标记了集合M,称Painter染了集合M中的一个独立集。
定理6:图G是一个色数为k的图,若对于任意正整数m,G都是在线 -列表可选的且
-列表可选的且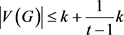 ,那么
,那么 也是在线
也是在线 -列表可选的。
-列表可选的。
证明:令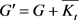 ,在游戏的第i步,我们令fi(v)表示v的现有筹码数,
,在游戏的第i步,我们令fi(v)表示v的现有筹码数, 表示v待染的颜色数。所以,
表示v待染的颜色数。所以, ,
, 。如果第i轮中,v被Lister选中,则
。如果第i轮中,v被Lister选中,则 ,若没被Lister选中,则
,若没被Lister选中,则 。若v被Painter染色,则
。若v被Painter染色,则 ,若v没被Painter染色,则
,若v没被Painter染色,则 ,根据定理5,如果
,根据定理5,如果 ,则我们可以把v点去掉。
,则我们可以把v点去掉。
记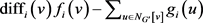 。我们关注游戏过程中对于T中的点v,
。我们关注游戏过程中对于T中的点v,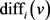 的值。若
的值。若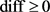 ,则点v在之后的游戏中就可以忽略不计。
,则点v在之后的游戏中就可以忽略不计。
若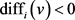 ,根据定义我们可以知道对于每个点v,游戏每进行一轮,
,根据定义我们可以知道对于每个点v,游戏每进行一轮, 的值都不会减小。尤其,如果某一回合点v没有被Lister选中而点v的邻居被Painter染色,则
的值都不会减小。尤其,如果某一回合点v没有被Lister选中而点v的邻居被Painter染色,则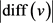 的值至少减少1。因此,当某一回合点v遇到这种情况时,我们就称点v赚到了一次。
的值至少减少1。因此,当某一回合点v遇到这种情况时,我们就称点v赚到了一次。
记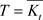 ,且
,且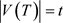 。我们要证明
。我们要证明 是在线
是在线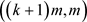 −列表可选的,也就是要证明在
−列表可选的,也就是要证明在 的在线
的在线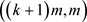 −染色游戏中,Painter有一个赢的策略。
−染色游戏中,Painter有一个赢的策略。
我们用 表示Painter在G的
表示Painter在G的 −在线染色游戏中用的策略。Painter在
−在线染色游戏中用的策略。Painter在 的在线
的在线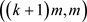 −染色游戏中,除了有m次的特殊回合出现的时采用其他策略外,其他的回合仍按照策略
−染色游戏中,除了有m次的特殊回合出现的时采用其他策略外,其他的回合仍按照策略 进行染色。
进行染色。
Painter采取的策略是:每次都根据策略 选择
选择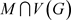 中的点染,除非情况(*)发生:
中的点染,除非情况(*)发生:
 中的每个点都已经至少赚了
中的每个点都已经至少赚了 次,其中
次,其中 。
。
当(*)发生的时候,Painter染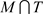 否则,Painter将根据策略
否则,Painter将根据策略 染
染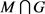 。
。
下面我们证明该策略是Painter的一个赢的策略。假设Painter使用该策略,Lister赢得游戏。
首先我们证明情形(*)至多发生了 次。
次。
假设情形(*)发生了m次,发生在游戏的第 轮,第
轮,第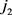 轮,...,
轮,..., 轮。记第i轮时,Lister选取的顶点的集合为
轮。记第i轮时,Lister选取的顶点的集合为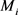 ,Painter染色的顶点集为
,Painter染色的顶点集为 。令
。令
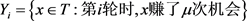
对任意 ,
, ,根据定义,x至少赚了
,根据定义,x至少赚了 次机会,而由于当x没有赚到时,即因为它被Lister选中了,因此x至多被Lister选中了
次机会,而由于当x没有赚到时,即因为它被Lister选中了,因此x至多被Lister选中了 次。即有
次。即有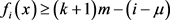 。
。
根据定义,

因此 。
。
根据情形(*)的定义,对 ,有
,有

且有,

所以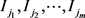 包含
包含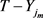 。即
。即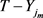 中的顶点在第
中的顶点在第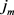 轮均已染色m次。而根据引理??,
轮均已染色m次。而根据引理??,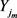 中的顶点均不需再考虑,故Painter只需将G中的顶点染色即可。因为G的每个顶点有
中的顶点均不需再考虑,故Painter只需将G中的顶点染色即可。因为G的每个顶点有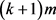 枚筹码,扣除上述m次情形(*),G的每个顶点还有
枚筹码,扣除上述m次情形(*),G的每个顶点还有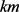 枚筹码。因此根据策略
枚筹码。因此根据策略 ,Painter可以将G的顶点染好。
,Painter可以将G的顶点染好。
即根据这个策略,Painter可以将 中的每个点都染到m个颜色。这与我们的假设相矛盾,因此情况(*)至多发生了
中的每个点都染到m个颜色。这与我们的假设相矛盾,因此情况(*)至多发生了 次。
次。
由于情况(*)至多发生了 次。对于T中的每一个点v而言,点v被标记同时被染色的次数至多有
次。对于T中的每一个点v而言,点v被标记同时被染色的次数至多有 次。且每当Painter染了T中的点时,T中没有点赚到一次机会。并且,对于Painter染了G中点时的每一回合,T中至少有一个点还没有赚到
次。且每当Painter染了T中的点时,T中没有点赚到一次机会。并且,对于Painter染了G中点时的每一回合,T中至少有一个点还没有赚到 次机会。故T中的每一个点v被Lister标记但是没被Painter染色的次数至多为
次机会。故T中的每一个点v被Lister标记但是没被Painter染色的次数至多为 次。
次。
否则 中的每个点都赚了
中的每个点都赚了 次机会,根据命题?? ,同理,
次机会,根据命题?? ,同理,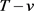 中的每个点都不需再考虑。在之后的游戏中,只要v被Lister选中,Painter就将其染色直到点v被Painter染了m次。这样Painter将赢得游戏,不符合假设条件。
中的每个点都不需再考虑。在之后的游戏中,只要v被Lister选中,Painter就将其染色直到点v被Painter染了m次。这样Painter将赢得游戏,不符合假设条件。
则此时v一共被Lister选中的次数至多为 次。我们可以发现对于T中的每一点v,v一共被Lister选中的次数少于
次。我们可以发现对于T中的每一点v,v一共被Lister选中的次数少于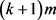 。因此Lister不可能赢得游戏。
。因此Lister不可能赢得游戏。
综上,在 的在线
的在线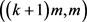 −染色游戏中,Painter有一个赢的策略。定理得证 ■
−染色游戏中,Painter有一个赢的策略。定理得证 ■
定理7:设G是一个图且 ,如果
,如果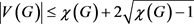 ,则对任意正整数m,G都是在线
,则对任意正整数m,G都是在线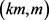 -列表可选。
-列表可选。
证明:令 。由于
。由于 ,我们可以假设G是一个完全k-部图。设
,我们可以假设G是一个完全k-部图。设 为图G中点数为1的部集的个数,其中
为图G中点数为1的部集的个数,其中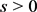 。否则,G中没有点数为1的部集,则
。否则,G中没有点数为1的部集,则 ,这和图G的点数矛盾。称图G中点数为1的部集中的点为单点。我们将对
,这和图G的点数矛盾。称图G中点数为1的部集中的点为单点。我们将对 进行归纳。
进行归纳。
当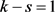 时,图G可以看成是由
时,图G可以看成是由 联合一个点数为
联合一个点数为 的独立集T得到的图。根据定理6,G是在线
的独立集T得到的图。根据定理6,G是在线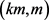 -列表可选的。
-列表可选的。
当 时,令T是点数最少的非单点的部集,其中
时,令T是点数最少的非单点的部集,其中 ,并且令
,并且令 。接下来我们将证明对任意正整数m,
。接下来我们将证明对任意正整数m, 都是在线
都是在线 -列表可选的,并且t的大小一定满足定理2.1的条件。
-列表可选的,并且t的大小一定满足定理2.1的条件。
我们希望 的点足够小使得我们可以利用归纳假设,也就是
的点足够小使得我们可以利用归纳假设,也就是

事实证明这是对的,因为当 且
且 时,
时,

接下来,我们将证明t的大小满足定理6的条件。我们希望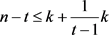 。也就是需要证明
。也就是需要证明 ,也就是
,也就是

该不等式成立且当 时,等号成立,定理得证。 ■
时,等号成立,定理得证。 ■
对于一个图G,如果把图中的每个点替换成一个完全图 ,如果两点在原图中是邻点,则在新图中对应的两个
,如果两点在原图中是邻点,则在新图中对应的两个 完全图中的点也对应是邻点,我们将由图G都经过这样变换得到的新图记为
完全图中的点也对应是邻点,我们将由图G都经过这样变换得到的新图记为 。如果对于任意正整数m,
。如果对于任意正整数m, ,则说明对任意正整数m,G都是在线
,则说明对任意正整数m,G都是在线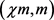 -可选的。
-可选的。
定理8:设G是一个独立数为a的图,且 ,若
,若
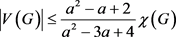
则对任意正整数m来说,G都是在线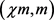 -可选的。
-可选的。
证明:因为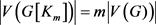 且
且 ,所以
,所以

因此 。根据定理可知,
。根据定理可知, 。则对任意正整数m来说,G都是在线
。则对任意正整数m来说,G都是在线 -可选的。 ■
-可选的。 ■
但是,这种方法不适用于Ohba猜想的多重列表染色的推广,只适用于点数与色数关系成比例的条件下列表染色的推广。同时,用此方法我们还可以得到以下结果。
定理9:设G是一个独立数为a的图,如果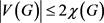 且
且 ,则对任意正整数m来说,G都是在线
,则对任意正整数m来说,G都是在线 -可选的。
-可选的。
文章引用
颜嘉燕. 多重在线列表染色
Multiple Online List Coloring[J]. 应用数学进展, 2020, 09(03): 408-413. https://doi.org/10.12677/AAM.2020.93049
参考文献
- 1. Zhu, X. (2009) On-Line List Colouring of Graphs. Electronic Journal of Combinatorics, 16, 3665-3677. https://doi.org/10.37236/216
- 2. Ohba, K. (2002) On Chromatic-Choosable Graphs. Journal of Graph Theory, 40, 130-135. https://doi.org/10.1002/jgt.10033
- 3. Noel, J.A.; Reed, B.A. and Wu, H. (2015) A Proof of a Conjecture of Ohba. Journal of Graph Theory, 79, 86-102. https://doi.org/10.1002/jgt.21819
- 4. Kozik, J., Micek, P. and Zhu, X. (2014) Towards an On-Line Version of Ohba’s Conjecture. European Journal of Combinatorics, 36, 110-121. https://doi.org/10.1016/j.ejc.2013.07.003
- 5. Carraher, J., Loeb, S., Mahoney, T., et al. (2014) Three Topics in Online List Coloring. Journal of Combinatorics, 5, 115-130. https://doi.org/10.4310/JOC.2014.v5.n1.a5
- 6. Dvo?ák, Z., Hu, X. and Sereni, J.-S. (2017) A 4-Choosable Graph That Is Not (8:2)-Choosable. Journal of Graph Theory, 1-4.