Advances in Applied Mathematics
Vol.
12
No.
01
(
2023
), Article ID:
60655
,
6
pages
10.12677/AAM.2023.121018
一类特殊坚韧图的性质
马惠,杨卫华*
太原理工大学,数学学院,山西 晋中
收稿日期:2022年12月19日;录用日期:2023年1月11日;发布日期:2023年1月29日

摘要
连通图G的坚韧度定义为 。如果G的坚韧度是t,并且删去G的任意一条边后其坚韧度减小,则称G是极小t-坚韧的。Matthews等证明了 -free图的连通度是其坚韧度的2倍。本文证明了坚韧度为t的 -free图的连通度不超过 ,且极小1-坚韧, -free图的连通度为2。此外,Kriesell猜想极小1-坚韧图的最小度是2。Katona等推广了上述猜想,极小t-坚韧图的最小度是 。本文证明了极小 -坚韧, -free图的最小度为1,其中 。
关键词
坚韧度,极小t-坚韧图,连通度,最小度, -free图

Properties of Some Class of Special Tough Graphs
Hui Ma, Weihua Yang*
School of Mathematics, Taiyuan University of Technology, Jinzhong Shanxi
Received: Dec. 19th, 2022; accepted: Jan. 11th, 2023; published: Jan. 29th, 2023

ABSTRACT
The toughness of G is defined as . A graph G is minimally t-tough if the toughness of G is t and the deletion of any edge from G decreases the toughness. Matthews et al. has proved that the connectivity of -free graphs is twice its toughness. This paper shows that the connectivity of -free graphs with toughness t is at most , and the connectivity of minimally 1-tough, -free graphs is 2. In addition, Kriesell conjectured that the minimum degree of minimally 1-graphs is 2. Katona et al. proposed a generalized version of the conjecture that the minimum degree of minimally t-tough graph is . This paper proves that the minimum degree of minimally -tough, -free graphs is 1, where .
Keywords:Toughness, Minimally t-Tough Graphs, Connectivity, Minimum Degree, -Free Graphs

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
是无向,有限阶的简单图。对于G的任意一点v, 是指G中相邻的点集, 是指G中与v关联的边的数目。用 表示G的顶点的最小度,用 表示G的连通度,且用 表示G的边连通度。对于任意点集 ,用 和 分别表示S和 的导出子图,并且用 表示 的分支个数。设S和T是G的子图或者 的子集,用 表示在 中与T中点相邻的点集,用 表示S与T之间的边集。
定义1.1:设G是一个非完全连通图,其坚韧度定义为:
如果G是完全图,则其坚韧度 ;如果G不连通,则其坚韧度 。
定义1.2:如果G的坚韧度为 ,那么称G是t-坚韧的。若G的割集S满足 ,则称S是G的坚韧集。
Chvátal [1] 在1973年首次提出坚韧度的定义,并提出了一个著名的猜想:存在正实数 ,使得每个 -坚韧图都是哈密顿图。之后,很多学者开始研究图的坚韧度和哈密顿图的关系。Thomassen给出了一个坚韧度为3/2的非哈密顿图:选择一个3-正则,3-连通且不存在哈密顿路的图G (Bermond [2] 证明了这样的图是存在的),将图中的每个点都替换成三角形后得到图H,Chvátal [3] 证明了 ,因此满足
Chvátal猜想的 。之后,Bauer等在 [1] 中证明了,任给 ,都存在一个 -坚韧,不包含哈
密顿路的图,因此 。在一些特殊的图类中,我们可以确定 的值。例如,10-坚韧弦图 [4] 和3/2-坚韧分离图 [5] 是哈密顿图;4-坚韧,2k-连通 -free图 [6] 是哈密顿图;2-坚韧, -free图 [7] 是哈密顿图;7-坚韧, -free图 [8] 是哈密顿图。此外,有些学者开始研究图的坚韧度和k-因子的关系 [9]。Enomoto等 [10] 给出了k-坚韧图有一个k-因子的充分条件是 是偶数。Bauer等 [1] 证明了每个3/2-坚韧,5-弦图都有一个2-因子。1999年,Broersma [11] 在研究2-坚韧图的哈密顿性的过程中给出了极小t-坚韧图的定义。
定义1.3:如果G的坚韧度为t,且对于任意一条边 都有 ,则称G是极小t-坚韧的。
由坚韧度的定义可知每个t-坚韧非完全图都是2t-连通的,因此t-坚韧图的最小度至少是 。在 [12] 中,Mader [13] 证明了极小k-连通图的最小度为k。据此,Kriesell [7] 针对极小1-坚韧图提出了以下猜想。后来,Katona [12] 推广了他的猜想。
猜想1.4: [14] 每个极小1-坚韧图都有一个2度顶点。
猜想1.5: [12] 每个极小t-坚韧图都有一个 度顶点。
目前为止Kriesell的猜想还未被证明。2018年,Katona [12] 等给出了一个极小1-坚韧图最小度的上界,这是现在得到的最好的结果。虽然现在还没有证明Kriesell的猜想在所有图类上都成立,但是可以证明这个猜想在一些特殊图上成立,例如:Katona [12] 证明了极小1-坚韧, -free图的最小度是2。同样,推广的Kriesell猜想也被证明在一些特殊图类中成立。例如: [15] 中证明了极小t-坚韧弦图,分离图和 -free图的最小度为1,其中 。
定理1.6: [12] 每个极小1-坚韧图最小度不超过 。
根据极小t-坚韧图的定义,可以得到下面的命题。
命题1.7: [15] 设G是极小t-坚韧图,其中t是正实数。对于G的任意一条边e,
1) e是G的一条割边,或
2) 存在一个点集 满足: 和 ,且e是 的割边。
在第一种情况下,我们定义 。
本文主要研究t-坚韧, -free图的性质,并证明推广的Kriesell猜想在极小 -坚韧, -free图上成立。下面我们给出了 -free图的定义。
定义1.8:如果G不包含 包含作为它的导出子图,则称G是 -free图。
2. 主要结论及其证明
2.1. t-坚韧, -Free图的连通度
在这一节中,我们研究t-坚韧, -free图的连通度。Matthews等 [16] 证明了 -free图的坚韧度和连通度有以下关系。
定理2.1: [16] 如果G是非完全 -free图,那么 。
设 。对于 -free图,上述定理中的等式不成立。例如: 的坚韧度是1,但其连通度是 ,但其连通度是 。下面我们给出了一个t-坚韧, -free图的连通度的上界。
定理2.2:设G是非完全 -free图,其中 。下面的结论成立。
(i) 。
(ii) 如果 且 ,那么 或者对于G的坚韧集S, 的每个分支在S中有且仅有三个邻点,且S中的每个点都与 的每个分支相邻。
证明:由坚韧度的定义知,图G中存在割集S满足 。将 的每个分支都收缩到一个点,用S表示这些点的集合,并将S与T之间的重边删掉。由于G是 -free图,所以S中的每个点都与T中的最多 个邻点相邻,从而 。另一方面,由于T中的每个点在S中至少有 个邻点,所以可以得到 。因此 ,从而 。
由上面的证明知,当 且 时,有 。如果 ,由 知 。这时 的每个分支在S中有且仅有三个邻点,且S中的每个点都与 的每个分支相邻。
由上面的定理知,坚韧度为1的 -free图的连通度不一定为2,若Kriesell的猜想正确,则极小1-坚韧, -free图的连通度是2。
定理2.3:极小1-坚韧, -free图的连通度是2。
证明:设G是极小1-坚韧, -free图。假设 ,由 知中G没有割边。
任给边 ,设 是满足命题1.6的点集。由于e不是割边,所以 且 。这时 ,否则 或 是G的一个二点割,这与 矛盾。因此 ,即 是G的坚韧集。设 是 中包含边e的分支,且 和 分别表示 中包含u和v的分支。由定理2.2 (ii)知,可设 。若 ,由 ,容易得到 且 。再由 ,可得 。不妨设 。根据引理2.2 (ii),点 和 中除 外的另外两个分支相邻。显然, 中包含一个 子图,与G是 -free图矛盾。因此 。同理, 。由于 ,我们可以设 且 。
令 。设 是满足定理1.6的点集。类似于 的讨论,我们可以证明 也是G的坚韧集。显然, 。由定理2.2 (ii)知,点v与 的三个分支相邻。而 ,所以 ,这与 矛盾。
因此 。再由 知 。
2.2. 极小 -坚韧, -Free图
在这一节中,我们将研究极小 -坚韧, -free图的最小度。Katona等在 [4] [10] 中给出了极小1/2-坚韧和极小1-坚韧, -free图的结构。
定理2.4: [15] 极小1/2-坚韧, free图可以用下面的方式构造。
1) 任取一颗最大度为3的树,且树中所有3度点和1度点组成的点集是独立集。
2) 删掉每个度为3的点v,然后将v在树中每个邻点用一个三角形连接起来。
定理2.5: [12] 点数大于3的极小1-坚韧, -free图都是圈。
由上面的定理知,对于极小1/2-坚韧和极小1-坚韧, -free图,Kriesell的猜想是正确的。下面我们将研究,当 时,极小 -坚韧, -free图的最小度。由极小 -坚韧, -free图G的定义,容易得到以下引理。任给边 ,令 。
引理2.6:设G是极小 -坚韧, -free图。对于G的任意一条非割边e,
(i) 。
(ii) 有且仅有一个圈包含边e,且圈长为3。
证明:对于G的任意一条非割边e,由命题1.6知存在一个非空点集 满足
。
这时 。
将 的每个分支都收缩到一个点,用T表示这些点的集合,并将 与T之间的重边删掉。由于G是 -free图,所以S中的每个点都与T中的最多 个邻点相邻,从而 。另一方面,由G是连通图知T中的每个点在 中至少有1个邻点,所以 。故有
。
由 知 。因此 的每个分支在 中有且仅有一个邻点,且 中的每个点都与 的 个分支相邻。
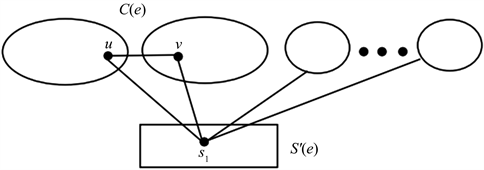
设 是 中包含边e的分支,令 。因为在 中与 相邻的 个分支不与 中的点相邻,所以 。不难看出 是满足命题1.6的点集,所以 (见图1)。
图1.
由于e是非割边,所以G中至少有一个圈包含边e。再由 知包含边e的圈一定包含 。设e的两个端点分别是u和v。因为 与 的 个分支相邻且G是 -free的,所以 ,即e只包含在三角形 中。
定理2.7:设 。极小 -坚韧, -free图的最小度是1。
证明:设G是极小 -坚韧, -free图。对于G的每个三角形,删掉三角形的三条边,然后增加一个点,将每个点与原来三角形的三个点连边。把G经过上述操作后得到的图记为H。由引理2.6 (ii)知G中的所有圈都是三角形,因此H是树。
下面我们将证明H中的每个叶子节点都是G中的1度点。假设H中存在一个叶子节点s不是G中的1度点。由H的构造过程知G中有且仅有一个三角形包含点s且 ,设这个三角形的点集为 。令 ,设 是满足命题1.6的点集,且 。由引理2.6 (i)知 。由命题1.6知 。由G是连通图且 ,所以 ,矛盾。
3. 结论
根据坚韧度的定义,我们可以得到t-坚韧图的连通度是2t-连通的,但是其连通度不一定为2t。对于一些特殊图类,我们可以确定图的坚韧度和连通度的关系。Matthews等 [16] 证明了坚韧度为t的 -free图的连通度是2t。由本文的定理2.2 (i)知,坚韧度小于2/3的 -free图的连通度为1,坚韧度大于等于2/3且小于1的 -free图的连通度是2且坚韧度为1的 -free图的连通度不超过3。Kriesell [14] 猜想极小1-坚韧图的最小度为2。由 知,如果Kriesell的猜想正确,容易推知极小1-坚韧图的连通度是2。本文证明了极小1-坚韧, -free图的连通度为2。Katona [12] 将Kriesell的猜想推广到了2t上。本文证明了对于极小 -坚韧, -free图,推广的Kriesell的猜想是正确的。
基金项目
山西省基础研究项目(20210302123097)。
文章引用
马 惠,杨卫华. 一类特殊坚韧图的性质
Properties of Some Class of Special Tough Graphs[J]. 应用数学进展, 2023, 12(01): 147-152. https://doi.org/10.12677/AAM.2023.121018
参考文献
- 1. Chvátal, V. (2006) Tough Graphs and Hamiltonian Circuits. Discrete Mathematics, 306, 910-917. https://doi.org/10.1016/j.disc.2006.03.011
- 2. Bermond, J.C. (1978) Hamiltonian Graphs. In: Beineke, L. and Wilson, R.J., Eds., Seleted Topics in Graph Theorey, Academic Press, London, 127-167.
- 3. Bauer, D., Katona, G.Y., Kratsch, D. and Veldman, H.J. (2000) Chordality and 2-Factors in Tough Graphs. Discrete Applied Mathematics, 99, 323-329. https://doi.org/10.1016/S0166-218X(99)00142-0
- 4. Kabel, A. and Kaiser, T. (2017) 10-Tough Chordal Graphs Are Hamiltonian. Journal of Combinatorial Theory, Series B, 122, 417-427. https://doi.org/10.1016/j.jctb.2016.07.002
- 5. Kratsh, D., Lehel, J. and Müller, H. (1996) Toughness, Hamiltonic-ity and Split Graphs. Discrete Mathematics, 150, 231-245. https://doi.org/10.1016/0012-365X(95)00190-8
- 6. Shi, L. and Shan, S. (2022) A Note on Hamiltonian Cycles in 4-Tough -Free Graphs. Discrete Mathematics, 345, Article ID: 113081. https://doi.org/10.1016/j.disc.2022.113081
- 7. Ota, K. and Sanka, M. (2022) Hamiltonian Cycles in 2-Tough -Free Graphs. Journal of Graph Theory, 101, 769-781. https://doi.org/10.1002/jgt.22852
- 8. Gao, Y. and Shan, S. (2022) Hamiltonian Cycles in 7-Tough -Free Graphs. Discrete Mathematics, 345, Article ID: 113069. https://doi.org/10.1016/j.disc.2022.113069
- 9. Lu, H. and Kano, M. (2020) Characterization of 1-Tough Graphs Using Factors. Discrete Mathematics, 343, Article ID: 111901. https://doi.org/10.1016/j.disc.2020.111901
- 10. Enomoto, H., Jackson, B., Katerinis, P. and Saito, A. (1985) Toughness and the Existence of k-Factors. Journal of Graph Theory, 9, 87-95. https://doi.org/10.1002/jgt.3190090106
- 11. Broersma, H., Engbers, E. and Trommel, H. (1999) Various Results on the Toughness of Graphs. Networks, 33, 233-238. https://doi.org/10.1002/(SICI)1097-0037(199905)33:3<233::AID-NET9>3.0.CO;2-A
- 12. Katona, G.Y., Soltesz, D. and Varga, K. (2018) Properties of Minimally t-Tough Graphs. Discrete Mathematics, 341, 221-231. https://doi.org/10.1016/j.disc.2017.08.033
- 13. Mader, W. (1971) Eine Eigenschaft der Atome endlicher Graphen. Archiv der Mathematik, 22, 333-336. https://doi.org/10.1007/BF01222585
- 14. Kaiser, T. (2003) Problems from the Workshop on Dominating Cycles. http://iti.zcu.cz/history/2003/Hajek/problems/hajek-problems.ps
- 15. Katona, G.Y. and Varga, K. (2018) Minimally Toughness in Special Graph Classes. ArXiv: 1802.00055.
- 16. Matthews, M.M. and Sumner, D.P. (1984) Hamiltonian Results in -Free Graphs. Journal of Graph Theory, 8, 139-146. https://doi.org/10.1002/jgt.3190080116
NOTES
*通讯作者。