Advances in Education
Vol.
12
No.
06
(
2022
), Article ID:
52690
,
8
pages
10.12677/AE.2022.126297
火箭所受空气动力必在总攻角平面的 理解与教学
张学阳,张雅声,周海俊,程文华
航天工程大学,北京
收稿日期:2022年5月10日;录用日期:2022年6月13日;发布日期:2022年6月22日

摘要
火箭(或导弹)所受空气动力必在总攻角平面的结论,是利用总攻角分析零攻角再入、以配平攻角飞行等典型的再入段运动的基础,但在现行弹道轨道动力学的教材中,往往不加证明地给出这一并不显然的结论,在教学中容易引起学生的困惑,也不利于学生掌握这一结论。针对这一问题,综合应用速度坐标系与箭体坐标系的变换关系、火箭气动系数的对称关系以及小角度三角函数的近似计算,给出了该结论的两种证法与分析,指出这个结论的证明依赖于火箭气动系数的对称关系,可以推广至返回与再入段的弹头或返回舱。证明过程的综合性较强,可帮助学生对前期所学知识融会贯通,同时这一证明也是运用纯数学工具解决工科专业问题的典型范例,有助于培养工科学生的应用数学思维,提高学生的数学建模能力。
关键词
空气动力,总攻角平面,总攻角,数学思维,数学建模,工科教学

Approach to Teaching That the Aerodynamic Force on the Rocket Must Be in the Plane of the Total Angle of Attack
Xueyang Zhang, Yasheng Zhang, Haijun Zhou, Wenhua Cheng
Space Engineering University, Beijing
Received: May 10th, 2022; accepted: Jun. 13th, 2022; published: Jun. 22nd, 2022

ABSTRACT
The conclusion that the aerodynamic force of the rocket (or missile) must be in the plane of total angle of attack is often given without proof in the current textbook of ballistic trajectory dynamics, but this is not an obvious conclusion, which is easy to cause students’ confusion in teaching. To solve this problem, two proofs and analysis of this conclusion are given by comprehensively applying the transformation relationship between the velocity coordinate system and the body coordinate system, the symmetry relationship of the rocket aerodynamic coefficient and the approximate calculation of trigonometric functions with the small angle. It is pointed out that the proof of this conclusion depends on the symmetry relationship of the rocket aerodynamic coefficient and can be extended to the warhead or return capsule in the return and reentry phase. The proof process is highly comprehensive and is very suitable to be explained as a typical example, which is helpful for students to master the previous knowledge. At the same time, this proof is also a typical example of using pure mathematical tools to solve engineering problems, which is helpful to cultivate engineering students’ applied mathematical thinking and improve students’ mathematical modeling ability.
Keywords:Aerodynamic Force, Plane of Total Angle of Attack, Total Angle of Attack, Mathematical Thinking, Mathematical Modeling, Engineering Teaching

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
对于火箭(或导弹,下省略)的运动来说,总攻角是指导弹速度方向与箭体(或弹体,下省略)纵对称轴的夹角 [1],以区别于攻角。攻角是指速度在箭体主对称面内的投影,与纵对称轴的夹角 [1]。显然,总攻角要比攻角的定义更加简单,在对火箭运动进行刻画时,具有重要作用,是一个非常重要的概念。
总攻角平面是指由火箭纵对称轴与速度确定的平面 [1],火箭所受气动力必在总攻角平面的结论,是利用总攻角分析零攻角再入、以配平攻角飞行等典型的再入段运动的基础 [1],但是现行的弹道轨道动力学教材中 [1] - [6],往往不加证明地给出这一结论,并在此结论的基础上进行相关推导与计算。然而这并不是一个显然的结论,授课时每次讲到这里,学生都表示不理解,让学生自己思考,也鲜有学生能够完成证明。
本文综合应用速度坐标系与箭体坐标系的变换关系、火箭气动系数的对称关系以及小角度三角函数的近似计算,给出该结论的两种证明,证明过程综合性较强,非常适合作为典型例题讲解,有助于学生对前期所学知识的融会贯通。
2. 坐标系定义
2.1. 箭体坐标系
如图1所示,该坐标系原点 位于火箭的质心,各坐标轴的定义如下:
1) 轴:与箭体的纵对称轴一致,指向箭体的头部。
2) 轴:垂直于 轴,且位于箭体主对称面(即火箭发射瞬时与射击平面重合的平面)内,指向上方。
3) 轴:满足右手直角坐标系准则。

Figure 1. Rocket body frame and velocity frame
图1. 箭体坐标系与速度坐标系
箭体坐标系通常用字符B表示。
2.2. 速度坐标系
如图1所示,该坐标系原点 位于火箭的质心,各坐标轴的定义如下:
1) 轴:沿火箭的飞行速度方向。
2) 轴:在火箭的主对称面内,垂直于 轴;通过满足右手直角坐标系准则来确定其方向。
3) 轴:垂直于 平面,顺着飞行方向看去 轴指向右方。
速度坐标系通常用字符V表示。
2.3. 速度坐标系V与箭体坐标系B间的方向余弦阵
如图2所示,速度坐标系与箭体坐标系间的方向余弦阵为
(1)
其中M2与M3为初等转换矩阵,两个欧拉角 的定义如下:
1) 角 称为攻角,为导弹速度矢量 在导弹主对称面 内的投影与弹体轴 间的夹角,且投影在 轴下方为正。
2) 角 称为侧滑角,为导弹速度矢量 与弹体主对称面 间的夹角,且顺 轴正向看,速度矢量 在主对称面右边为正。
在火箭的实际飞行中, 的数值均很小。
由于箭体坐标系与速度坐标系的坐标原点重合,都在箭体质心,所以,将速度坐标系中的坐标 转换成箭体坐标系中的坐标 的关系式为
(2)
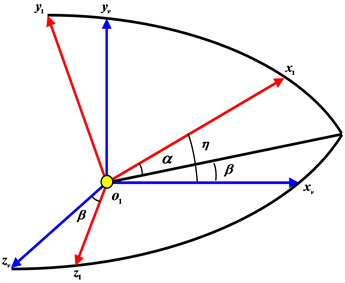
Figure 2. Conversion diagram from velocity frame to rocket body frame
图2. 速度坐标系与箭体坐标系的关系图
2.4. 总攻角
如图2所示,总攻角为速度轴o1xv与箭体纵轴o1x1之间的夹角,记为η。速度轴o1xv与箭体纵轴o1x1确定的平面x1o1xv,称为总攻角平面。
3. 空气动力的表示
如果物体与大气有相对运动,此时作用在物体上的大气压强不是处处相等,从而产生了不平衡的大气压强的合作用力,即空气动力。因此,空气动力是由物体外表面上压强分布不同而造成的,即空气动力是物体外表面压强差的合作用力,通常以符号 表示,即
(3)
其中: 为空气密度, 称为速度头,V为火箭相对于大气的飞行速度, 为火箭的特征面积(取其最大横截面积), 为无因次空气动力系数。
3.1. 空气动力在不同坐标系中的表示形式
根据空气动力 在不同坐标系中的投影,可以表示成不同的坐标。若将空气动力 投影到速度坐标系,则 的坐标为 ,三个分量分别称为阻力、升力和侧力,且
(4)
其中: 、 、 分别称为空气阻力系数、升力系数和侧力系数。
若将空气动力 投影到箭体坐标系,则 的坐标为 ,三个分量分别称为轴向力、法向力和横向力,且
(5)
其中: 、 、 称为轴向力系数、法向力系数和横向力系数。
3.2. 气动系数
由空气动力产生的原理可知,升力 和法向力 与攻角 有关,侧力 和横向力 与侧滑角 有关,即
(6)
(7)
因为火箭为轴对称物体,所以,根据力的定义有
(8)
4. 空气动力在总攻角平面的证明
欲证命题:火箭所受的空气动力 必定在总攻角平面x1o1xv内。
分析:欲证明一个矢量位于一个平面内,是典型的线性代数问题 [7],有两种思路,第一种是证明该矢量与平面的法向量垂直,第二种是证明该矢量可表示为平面两个矢量的线性组合,下面将分别按这两种思路进行证明。
4.1. 通过证明空气动力与总攻角平面的法向量垂直得证
证明1:箭体纵轴o1x1的单位矢量在箭体坐标系下的坐标为
速度轴o1xv的单位矢量在箭体坐标系下的坐标,可以由速度坐标系与箭体坐标系间的方向余弦阵式(1)得到:
则箭体坐标系下平面x1o1xv的法向量为
气动力 在箭体坐标系下的坐标为
则
代入式(6)、式(7)与式(8),可得
(9)
因为 为小角度,可以近似认为
(10)
从而
即
故空气动力 必在平面x1o1xv内。证毕。
4.2. 通过证明空气动力可表示为总攻角平面内两个矢量的线性组合得证
证明2:已知箭体坐标系下空气动力 的坐标为 ,与箭体纵轴o1x1轴向力的坐标为
空气动力 在速度坐标系速度轴o1xv上分量阻力的坐标为
由速度坐标系与箭体坐标系间的方向余弦阵式(1)可得,箭体坐标系下阻力的坐标为
对常数 ,在箭体坐标系下有
(11)
因为 为小角度,可以近似认为
(12)
将式(12)代入式(11),可得:
(13)
令 ,则
(14)
结合式(5),(6),(7),(8),可得:
(15)
令 ,可得:
(16)
由式(14),(15),(16)可得:
(17)
即空气动力 可以表示为 和 的线性组合,从而必在 和 确定的平面内,也就是平面x1o1xv内。证毕。
4.3. 证明小结
可以看到,证明过程的综合性较强,两种证明方法都综合应用了速度坐标系与箭体坐标系的变换关系(式(1))、火箭气动系数的对称关系(式(6)、(7)、(8))以及小角度三角函数的近似计算(式(10)、(12)),火箭所受的空气动力必定在总攻角平面的结论依赖于两点:
1) 攻角 和侧滑角 为小角度;
2) 火箭气动系数的对称关系,即 ,这来自于火箭外形的对称性。
对于返回与再入段的弹头或返回舱而言,这两个前提条件也是成立的,故其所受气动力也必在总攻角平面内,这是现行教材中分析返回与再入段运动的一个基础。
5. 总结
针对现行教材中火箭(或导弹)所受空气动力必在总攻角平面的这一结论,综合应用速度坐标系与箭体坐标系的变换关系、气动力系数关系以及小角度三角函数近似关系,给出了该结论的两种证法与分析,指出这个结论的证明依赖于火箭气动系数的对称关系,可以推广至返回与再入段的弹头或返回舱。证明过程的综合性较强,在教学实践中,证明一更为简洁,非常适合作为典型例题讲解,可帮助学生对前期所学知识融会贯通,证明二相对繁琐,在讲解了证明一的基础上,可作为课后作业由学生完成。同时,本证明是纯数学工具(《线性代数》知识)在工科专业课中的典型应用,小角度假设及其三角函数近似关系是运用数学工具解决工程问题的常用近似假设,证明过程有助于培养工科学生的应用数学思维,提高学生的数学建模能力。
基金项目
全军重点院校建设精品课程建设工程“弹道与轨道基础”(4142ZK314)、航天工程大学重点课程建设项目“弹道与轨道基础”(4142ZF1)、航天工程大学教学研究暨教学成果立项培育计划课题“《弹道与轨道基础》精品课程建设研究”(4142Z1)资助。
文章引用
张学阳,张雅声,周海俊,程文华. 火箭所受空气动力必在总攻角平面的理解与教学
Approach to Teaching That the Aerodynamic Force on the Rocket Must Be in the Plane of the Total Angle of Attack[J]. 教育进展, 2022, 12(06): 1955-1962. https://doi.org/10.12677/AE.2022.126297
参考文献
- 1. 张雅声. 弹道与轨道基础[M]. 北京: 国防工业出版社, 2019.
- 2. 于小红, 张雅声, 等. 发射弹道与轨道基础[M]. 北京: 国防工业出版社, 2007.
- 3. 王志刚, 施志佳. 远程火箭与卫星轨道力学基础[M]. 西安: 西北工业大学出版社, 2006.
- 4. 方群, 李兴国, 等. 航天飞行动力学[M]. 西安: 西北工业大学出版社, 2015.
- 5. 曾颖超. 航天器飞行力学[M]. 西安: 西北工业大学出版社, 1993.
- 6. 陈克俊, 刘鲁华, 等. 远程火箭飞行动力学与制导[M]. 北京: 国防工业出版社, 2014.
- 7. 同济大学数学系. 线性代数[M]. 第六版. 北京: 高等教育出版社, 2014.