Pure Mathematics
Vol.
12
No.
12
(
2022
), Article ID:
59880
,
14
pages
10.12677/PM.2022.1212239
带有反循环结构的三维近爱因斯坦流形
黄志明,卢卫君,孔祥硕
广西民族大学数学与物理学院,广西 南宁
收稿日期:2022年11月26日;录用日期:2022年12月22日;发布日期:2022年12月30日

摘要
三维黎曼流形上添加一个局部分量为Toeplitz矩阵的循环结构,可以应用于线性编码、图论、震动分析和调和伯格曼空间的研究等。而带有反循环结构的黎曼流形与爱因斯坦流形有着密切联系。本文从反循环角度出发,研究带有反循环结构的三维黎曼流形,给出反循环结构相容的等价条件。并利用反循环结构构建新的度量,结合新的度量证明这种流形是近爱因斯坦流形,进而给出近爱因斯坦流形的一些曲率特性。最后给出反循环结构作用到李群上的例子。
关键词
Toeplitz矩阵,反循环结构,相容性,近爱因斯坦流形,李群

Three-Dimensional Almost Einstein Manifolds with Skew-Circulant Structures
Zhiming Huang, Weijun Lu, Xiangshuo Kong
School of Mathematics and Physics, Guangxi Minzu University, Nanning Guangxi
Received: Nov. 26th, 2022; accepted: Dec. 22nd, 2022; published: Dec. 30th, 2022

ABSTRACT
An imposing circulant structure with local components of Toeplitz matrices on three-dimensional Riemannian manifolds can be applied to the linear coding, graph theory, vibration analysis and the study of harmonic Bergman space. The Riemannian manifold with skew-circulant structure whose local components are skew-circulant matrices is closely related to Einstein manifold. In this paper, from the point of view of skew-circulant structure, the equivalent conditions compatible with the skew-circulant structure are obtained, and some new metrics are constructed by using the skew-circulant structure. Combined with the new metric, it is showed that this kind of manifold with skew-circulant structure is an almost Einstein manifold, and then some curvature properties of the almost Einstein manifold are derived. Finally, an example of skew-circulant structure acting on Lie groups is given.
Keywords:Toeplitz Matrix, Skew-Circulant Structure, Compatibility, Almost Einstein Manifold, Lie Group

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
黎曼流形上的微分结构、拓扑结构、度量结构、附加结构等在几何研究中扮演着重要的角色。带有附加几何结构的黎曼流形是众多几何学者的主要研究对象之一。这种附加几何结构与黎曼曲率张量、里奇曲率张量、数量曲率、截面曲率往往有着密切的关联。若附加的几何结构能够以更具体的形式表示出来,比如矩阵形式,那么研究工作将能更加顺利进行。
主对角线上的元素相等,平行于主对角线的线上的元素也相等的矩阵叫做Toeplitz矩阵,简称为T型矩阵。这种矩阵主要应用于几何 [1]、线性编码 [2]、图论 [3]、震动分析 [4]。黎曼流形上添加一个额外的循环结构,这个结构在局部坐标基底下的分量矩阵是循环矩阵(Toeplitz矩阵),带有这种循环结构的黎曼流形已被广泛研究。在文献 [5] 中,Dzhelepov等学者在三维黎曼流形上引入满足三阶恒等的循环结构Q。
是一个三维黎曼流形,考虑在每一点p对应的切空间
有一个
型张量Q,Q在局部坐标基底
下形成一个循环矩阵,如下
, (1.1)
这个循环矩阵满足性质
, (1.2)
这个循环结构在局部坐标基底下的分量是全为1的循环矩阵。在文献 [6] [7] [8] [9] [10] 中,他们对带有循环结构的三维黎曼流形进行更进一步的研究,给出了黎曼曲率分量的具体表达式,也得到了很多有趣的几何特征。通过循环结构构建新的度量关系,给出了不同度量下的曲率关系 [11] [12] 和物理中的应用 [13] [14]。
在上述关于文献的启迪下,本文研究带有反循环结构的三维黎曼流形,且反循环结构S满足三阶反恒等关系
。这个反循环结构的分量矩阵是一个反循环的Toeplitz矩阵。从反循环角度出发,获得了反循环结构的相容性等价条件。利用这个反循环结构构建新的度量关系,证明带有反循环结构的三维黎曼流形是近爱因斯坦流形的证明过程,进而给出里奇曲率表达式中
、
满足一定条件下为常数。
论文组织结构如下:在第二节中,在考虑反循环结构与黎曼联络相容的前提下,推出黎曼曲率张量满足性质
和
,并利用反循环结构的特性构造新的度量关系。在第三节中,根据联络系数公式,计算出流形黎曼度量所对应联络系数。在假设反循环结构是相容的前提下,引出相容性的等价条件,同时也给出第二节中两个性质的等价条件。在第四节中,根据已有的定义进行拓展,给出近爱因斯坦流形的定义,并证明在反循环结构下的三维黎曼流形
是近爱因斯坦流形,继而给出相关系数的关系。结合新的度量关系,给出在不同度量结构下的里奇曲率关系和截面曲率关系。最后给出带有反循环结构的三维实连通李群是近爱因斯坦流形的例子。
2. 预备知识
首先给出部分黎曼几何的知识 [15] [16],
定义2.1. 设
为m维黎曼流形,
是与g相容的黎曼联络,则对
,定义映射
,如下
, (2.1)
这里的
称为黎曼流形
关于光滑切向量场X、Y的曲率算子。
定义2.2. 流形
上的
型的黎曼曲率张量
,
对
,黎曼曲率张量也可以表示为
. (2.2)
定义2.3. 设
为m维黎曼流形,
为黎曼联络,对
,由
, (2.3)
决定了一个
的2阶协变张量场,称为里奇张量场。如果
为
的规范正交基,则对
,
,
其中里奇曲率的分量
。
定义2.4. 设
是m维黎曼流形,
, 为
的规范正交基,数值
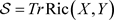 , (2.4)
, (2.4)
称为黎曼流形
在p点的数量曲率。在局部坐标系下,数量曲率的表达式,如下
. (2.5)
本文在
上的每一点p对应的切空间
考虑一个
型张量S,S在局部坐标基底
下形成一个反循环矩阵,如下
. (2.6)
这个反循环矩阵满足性质
. (2.7)
假设黎曼度量g和结构S满足
. (2.8)
由(2.6),(2.8)可得度量g在局部坐标基底
下的分量矩阵和逆矩阵,如下
,, (2.9)
这里
, 和
是在点
的光滑函数。如果光滑函数a,b之间满足
.
即度量g是正定的。带有反循环结构S的黎曼流形可以通过
来表示。
接下来考虑反循环结构S与黎曼联络是相容的,即
. (2.10)
命题2.5. 对于流形
,若反循环结构S是相容的,则对
,黎曼曲率张量满足
. (2.11)
证明:由于
,有
, (2.12)
由(2.1),有
。又由
,
可得
,
证毕。
根据(2.11),可以进一步推出
. (2.13)
接下来, 结合反循环结构S给出
,,, 的表达式
,,,, (2.14)
这里
,。
在反循环结构S下构造与黎曼度量g相关联的度量,关联度量与
、
、
、
的关系如下
,, (2.15)
,. (2.16)
度量
在局部坐标基底
下的分量矩阵和逆矩阵如下
,, (2.17)
这里
,度量
是一个负定度量。度量
在局部坐标基底
下的分量矩阵和逆矩阵如下
,,(2.18)
这里
,度量
是一个正定度量。
3. 反循环结构下的几何性质
是一个三维黎曼流形,
是在点
的切空间
的正交基底。联络系数
的公式如下
, (3.1)
这里
。由(2.9),(3.1)得
, (3.2)
这里
,,,,。
3.1. 黎曼曲率性质的等价条件
下面考虑反循环结构S与黎曼联络
相容的前提下,给出反循环结构的相容性等价条件。
命题 3.1.在流形
中,反循环结构S与黎曼联络
相容,即满足(2.11),当且仅当
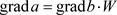 , (3.3)
, (3.3)
这里
。
证明:S是相容的,即
。在局部坐标表示下,满足
, (3.4)
这里
。由(2.6),上式等价于
, (3.5)
即
, (3.6)
由(3.2),(3.6),则有
, (3.7)
这里
。
,,,即(3.3)得证。
反之,将
、
、
代入(3.2),则(3.6),(3.7)成立,再由(3.4)得
,证毕。
3.2. 黎曼曲率性质的等价条件
接下来,在考虑流形
的黎曼曲率张量分别满足性质(2.11)和(2.13)的前提下,给出对应的等价条件。
与
分别表示曲率张量R和里奇曲率张量Ric在局部基底
下的分量,那么有下面的命题。
命题3.2.
满足
,等价于以下条件成立
. (3.8)
证明:在局部坐标表示下,(2.11)的局部表达形式为
. (3.9)
由(2.6),(3.9)有
,,,
,,,
结合黎曼曲率张量的对称和反对称性质得(3.8)。
反之,根据黎曼曲率张量的对称和反对称性质,由(2.6)和(3.8),则可得到(3.9),即(2.11)成立,证毕。
命题 3.3.
满足
,等价于以下条件成立
,. (3.10)
证明:在局部坐标表示下,(2.13)的局部表达形式为
. (3.11)
根据(2.6),(3.11)有
,,,
,,,
结合黎曼曲率张量的对称和反对称性质得(3.10)。
反之,根据黎曼曲率张量的对称和反对称性质,由(2.6)与(3.10),可以得到(3.11),即(2.13)成立,证毕。
4. 近爱因斯坦流形
度量
和度量
对应的里奇曲率张量分量定义如下
,. (4.1)
命题4.1. 若
的黎曼曲率张量满足
,那么里奇曲率张量Ric,
, 的分量满足
,,, (4.2)
这里
。
4.1. 近爱因斯坦流形的证明
定义4.2. 如果一个m维
黎曼流形
的里奇曲率张量与黎曼度量g满足
,
且
为常数,则称
为爱因斯坦流形。
在文献 [17] 中,对于局部可分解的黎曼流形,定义了一类近爱因斯坦流形(almost爱因斯坦流形),这是一类比爱因斯坦流形性质更弱的流形。而在文献 [11] 中,关于带有循环结构的三维黎曼流形,结合度量
给出了新的近爱因斯坦流形的定义。在此定义基础上,我们对这个定义进一步拓展,给出以下定义。
定义4.3. 如果一个n维
黎曼流形
的里奇曲率张量满足
, (4.3)
这里
, 为光滑函数,
是指在黎曼度量g下通过反循环结构S限制所给出的相关联度量。则称带有结构S的黎曼流形
为近爱因斯坦流形。当
时,这种流形是爱因斯坦流形。
在局部坐标系下与度量
和度量
对应的数量曲率如下
,. (4.4)
定理4.4.
的黎曼曲率张量满足
,那么在度量g与度量
下,M是近爱因斯坦流形。
证明:根据(2.5),(2.9),(2.18),(4.4),数量曲率
与
表达式如下
,. (4.5)
由(4.5)可以得到
, (4.6)
由(2.9),(2.18),那么(4.6)可以表示为
,. (4.7)
根据(4.2)和(2.9),(2.18),(4.7)有
,
即
. (4.8)
证毕。
利用上述的证明方法,结合度量
,可以得到以下推论。
推论4.5.
的黎曼曲率张量满足
,在度量g与度量
下,M是近爱因斯坦流形。
下面,我们结合比安基恒等式给出近爱因斯坦流形
中,系数
和
的关系。
定理 4.6.在反循环结构S与黎曼联络相容的前提下,一个带有反循环结构S的三维黎曼流形
的满足
,且里奇曲率满足
, (4.9)
这里
,。则
为常数。且
,. (4.10)
证明:在局部坐标系下,度量
的分量
. (4.11)
为了方便,
记为
,则对
有
即
.
在三维黎曼流形
中,里奇曲率满足
.
局部坐标系下的里奇曲率分量满足
. (4.12)
由
, 以及(4.12)有
. (4.13)
根据命题4.1,有
。比安基第二恒等式为
. (4.14)
将
,,, 分别作用于(4.14)两边,有
,
,
,
.
对上述式子进行化简,可以得到
,,. (4.15)
由(4.15),通过指标求和可以得到(4.10),以及
, (4.16)
即
为常数,证毕。
4.2. 不同度量结构下的曲率关系
在
中,
。如果X是非零的,那么根据(2.6),有
,所以X与SX的夹角
。
定义4.7. 如果在切空间
中一组基的形式是
,那么就叫这组基为S基底,也可看作是向量X诱导了切空间
中的一个S基底。
命题4.8. 非零向量
诱导出切空间中一个S基底,当且仅当
. (4.17)
定义4.9. 里奇曲率张量在非零向量X的方向上的值,为
. (4.18)
命题4.10. 在度量g和度量
下,
是近爱因斯坦流形,如果非零向量X诱导一个S基底,那么在这个基底向量方向上的里奇曲率张量为
, (4.19)
这里
。
证明:根据(2.8),(2.16),(4.8)可以得到
.(4.20)
向量X诱导一个S基底,
,由(2.8),(2.16)得
, (4.21)
结合(4.18),(4.20),(4.21)则可得到(4.19),证毕。
流形
在满足
的前提下,度量g和度量
的数量曲率有着以下关系。
命题4.11. 在度量g与度量
下,流形
是近爱因斯坦流形,数量曲率满足
, (4.22)
这里
,。
证明:由黎曼几何中对于数量曲率与里奇曲率的关系可以表示为
, (4.23)
这里
。如果流形
是近爱因斯坦流形,那么里奇曲率的表达式(4.8)成立。由(2.6),(2.9),(2.16)可以得到
. (4.24)
由(2.10),(4.23)有
. (4.25)
又因为(2.6),得(4.22),证毕。
命题4.12. 在度量g与度量
下,流形
是近爱因斯坦流形,数量曲率满足
, (4.26)
这里的
,。
4.3. 反循环结构下的截面曲率
设
是两个不共线的切向量,
所张成的二维子空间
是黎曼流形M在p点的二维截面。
定义4.13. 在黎曼流形
中,
,对
,如果
,
那么
在点p的二维截面
的截面曲率可以表示为
. (4.27)
非零向量
诱导切空间
的一个S基底,就有二维截面
,,。
接下来讨论这些二维截面分别在条件(2.11)和(2.13)下的截面曲率关系。
命题4.14. 流形
满足
,如果非零向量X诱导S基底,那么对于这些二维截面的截面曲率,有
. (4.28)
证明:由(2.11),可得
. (4.29)
根据(4.29),对X、Y、Z、U进行替换,有
,
,
.
由上述式子有
,
即
. (4.30)
由(2.8)可知
. (4.31)
由(4.31),可得
, (4.32)
由于
,
. (4.33)
结合(4.27),(4.30),(4.31),(4.33),得(4.28),证毕。
命题4.15. 流形
满足
,如果非零向量X诱导S基底,那么对于这些二维截面的截面曲率,有
.
证明:由(2.13),得
. (4.34)
根据(4.34),对Y、Z、U进行替换,有
. (4.35)
结合(4.27),(4.31),(4.35),得
,证毕。
5. 带有反循环结构的李群
在这一节中,讨论带有反循环结构S的李群,给出带有反循环结构的三维实连通李群是近爱因斯坦流形的例子。
首先,考虑一个
型基本张量F以及两个1-形式
, (5.1)
,. (5.2)
可以看出
,即
. (5.3)
根据(5.1)可以得到基本张量F在局部坐标系下的分量
,结合基本张量F的分量
以及两个1-形式,通过计算可以得到以下关系
.
定理5.1. 张量F满足
, (5.4)
这里
。
G是一个三维实连通李群,且李代数
是它的左不变向量场集合,李代数
的基底是
。在G中引入一个反循环结构S,且满足
,,, (5.5)
. (5.6)
流形
对于等式(2.7),(2.8)是成立的。关于李括号积满足
,,,, (5.7)
这里
,且
。根据(5.6),(2.15),度量
的分量如下
. (5.8)
利用Koszul公式
. (5.9)
可以得到
, 的表达式如下
,,,
,,
,,
,.
由(5.1)和
的表达式,可以得到基本张量F的分量
的第一种表达式以及1-形式
和
的表达式。然后根据定理5.1张量F的表达式,给出基本张量F的分量
的第二种表达式。
根据两种表达式相等,可以得出以下关系
,,. (5.10)
现在假设反循环结构S在李代数
中关于李括号积满足
. (5.11)
那么就有以下命题,
命题5.2. 三维李群
在李括号满足条件(5.11)下,这个李群是一个近爱因斯坦流形。
证明:李群满足条件(5.11),可以得到
. (5.12)
由(5.7),(5.12)有
,,. (5.13)
令
,,,那么(5.12)可以表示为
.(5.14)
又由(5.10)可知,
。根据(5.9)给出
的表达式
,,,
,,, (5.15)
,,
将上述
的表达式代入公式
,经过计算可以得到
,即
。再由命题2.5和命题3.2,有
.
再结合(2.1),(2.2),(5.6),(5.14)和(5.15),可以得到
. (5.16)
通过计算得到里奇曲率的分量
,. (5.17)
进一步得到的数量曲率
和
如下
,. (5.18)
根据(5.6),(5.8),(5.17),(5.18),里奇曲率张量满足
.
所以带有反循环结构的三维李群
是近爱因斯坦流形。
基金项目
课题由项目12061014,2019GXNSFAA245043资助。
文章引用
黄志明,卢卫君,孔祥硕. 带有反循环结构的三维近爱因斯坦流形
Three-Dimensional Almost Einstein Manifolds with Skew-Circulant Structures[J]. 理论数学, 2022, 12(12): 2217-2230. https://doi.org/10.12677/PM.2022.1212239
参考文献
- 1. Dzhelepov, G., Razpopov, D. and Dokuzova, I. (2010) Almost Conformal Transformation in a Class of Riemannian Manifolds.
- 2. Roth, R.M. and Lempel, A. (1990) Application of Circulant Matrices to the Construction and Decoding of Linear Codes. IEEE Transactions on Information Theory, 36, 1157-1163. https://doi.org/10.1109/18.57218
- 3. Muzychuk, M. (2004) A Solution of the Isomorphism Problem for Circulant Graphs. Proceedings of the London Mathematical Society, 88, 1-41. https://doi.org/10.1112/S0024611503014412
- 4. Olson, B., Shaw, S., Shi, C., et al. (2014) Circulant Matrices and Their Application to Vibration Analysis. Applied Mechanics Reviews, 66, Article ID: 040803. https://doi.org/10.1115/1.4027722
- 5. Dzhelepov, G., Dokuzova, I. and Razpopov, D. (2009) On a Three Di-mensional Riemannian Manifold with an Additional Structure.
- 6. Dokuzova, I., Razpopov, D. and Dzhelepov, G. (2017) Three-Dimensional Riemannian Manifolds with Circulant Structures. Advances in Mathematics: Scientific Journal, 7, 9-16.
- 7. Dokuzova, I. (2018) On a Riemannian Manifold with a Circulant Structure Whose Third Power Is the Identity. Filomat, 32, 3529-3539. https://doi.org/10.2298/FIL1810529D
- 8. Dokuzova, I. and Razpopov, D. (2010) On Affine Connections in a Riemannian Manifold with a Circulant Metric and Two Circulant Affinor Structures. Proceedings, 63, 63-70.
- 9. Dokuzova, I. (2015) Riemannian Manifolds with Two Circulant Structures. Journal of Geometry, 105, 529-538.
https://doi.org/10.1007/s00022-014-0218-2
- 10. Dzhelepov, G. (2022) On an Indefinite Metric on a 3-Dimensional Riemannian Manifold. International Journal of Geometry, 11, 12-19.
- 11. Dokuzova, I. (2020) On 3-Dimensional Almost Einstein Manifolds with Circulant Structures. Turkish Journal of Mathematics, 44, 1484-1497. https://doi.org/10.3906/mat-1904-97
- 12. Dokuzova, I. (2017) Almost Einstein Manifolds with Circulant Structures. Journal of the Korean Mathematical Society, 54, 1441-1456.
- 13. Razpopov, D. and Dzhelepov, G. (2020) The Value of the Work Done by an Isotropic Vector Force Field along an Isotropic Curve. IOP Conference Series: Materials Science and Engineering, 878, Article ID: 012021.
https://doi.org/10.1088/1757-899X/878/1/012021
- 14. Dzhelepov, G. (2017) Spheres and Circles with Respect to an Indefinite Metric on a Riemannian Manifold with Circulant Structures.
- 15. 陈维桓, 李兴校. 黎曼几何引论上册[M]. 北京: 北京大学出版社, 2004.
- 16. 徐森林, 薛春华. 微分几何[M]. 北京: 中国科学技术大学出版社, 1997.
- 17. Yano, K. (1965) Differential Geometry on Complex and Almost Complex Spaces. Pergamon Press, Ox-ford.






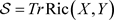 , (2.4)
, (2.4)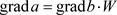 , (3.3)
, (3.3)