Pure Mathematics
Vol.
13
No.
06
(
2023
), Article ID:
67870
,
6
pages
10.12677/PM.2023.136175
双圈图的补图的谱半径
邱欢,王岚,王国平*
新疆师范大学数学科学学院,新疆 乌鲁木齐
收稿日期:2023年5月20日;录用日期:2023年6月21日;发布日期:2023年6月28日

摘要
设 是将 条悬挂边粘到 的一个三度点得到的双圈图。本文我们证明了n个点的双圈图的补图的最大谱半径只在 取到。
关键词
邻接矩阵,谱半径,补图

The Spectral Radius of the Complement of Bicyclic Graphs
Huan Qiu, Lan Wang, Guoping Wang*
School of Mathematical Sciences, Xinjiang Normal University, Urumqi Xinjiang
Received: May 20th, 2023; accepted: Jun. 21st, 2023; published: Jun. 28th, 2023

ABSTRACT
Let be the bicyclic graph obtained by attaching pendant edges to a vertex of degree 3 on . In this paper we show that the maximum spectral radiu is achieved uniquely by among all complements of bicyclic graphs of order n.
Keywords:Adjacency Matrix, Spectral Radius, Complement Graphs

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
设 是一个连通图,它的邻接矩阵 是一个 实对称矩阵。所以它的特征值都是实数,从大到小的排序为: ,其中最大的特征值 为图G的谱半径,记为 。刻画图的谱半径的文章很多,诸如文献 [1] [2] [3] 等。刻画带限制条件的谱的文章也很多,例如在文献 [4] 中作者刻画了具有完美匹配的双圈图的谱半径,文献 [5] 中作者刻画了有n个点k个悬挂点的双圈图的谱半径。相对来说刻画图的补图的谱半径的文章还不太多,在文献 [6] 中作者刻画了单圈图的补图的谱半径。本文主要刻画了双圈图补图的谱半径,以及谱半径达到最大时的极图。在本文中我们假设图G和它的补图 都是连通的,定义矩阵 的特征值 对应的特征向量为 ,其中 是点 对应的分量。
边数等于点数加一的连通图是双圈图。令 和 分别表示n个点的圈和路,我们定义图 是由两个点不交的圈 , 和一条路 组成的图形,其中 的两个端点分别和 , 有一个公共点,而当 和 有唯一的公共点时,我们记这个图形为 。定义图 为给定两个点中间连接有三条路 , 和 ,其中这三条路两两之间除了两个给定的点外没有公共点。我们把 和 粘上一些树构成的图形记作 ,把 粘上一些树构成的图形记作 。显然,所有n个点的双圈图由 和 组成。
设 是将 条悬挂边粘到 的一个三度点得到的双圈图。本文我们证明了n个点的双圈图的补图的最大谱半径只在 取到。
2. 主要结果
下面的定理在矩阵的研究中起到了非常重要的作用。
非负矩阵的Perron-Frobenius定理 [7] :如果M是一个 阶的非负不可约矩阵,那么有以下结论成立:
i) 若 是矩阵A的最大特征值,则 ;
ii) 是矩阵A的单重根;
iii) M有对应于特征值 的一个正的特征向量,使得 。
众所周知图G是连通图的充分必要条件是图G对应的邻接矩阵是不可约的。
引理1 [6] 假设u和v是图G的两个不同的点, ,其中 表示点v的邻点集。令 ,若 ,则有 成立。
假设u是图G的一个点, 是以v为根节点的一个l个点的树。我们将图G的u点和图 的v点粘接成一个点得到的图形记作 。接下来用 来表示以w为根节点的l个点的星图。由引理1容易得到下面的引理。
引理2 若图G, 和 如上所定义,那么有 ,其中等号成立的充分必要条件是 。
引理3 [6] 假设图G和 都是连通的,uv是图G的一条非悬挂的割边,图G压缩边uv为一个点w并给w带一条悬挂边得到的图形记作图 ,那么有 。
假设G与其补图 都是连通的。在接下来的内容里都用 表示 的对应于 的特征向量,其中 对应点v。
定理4 若 ,u是G的子图 的4度点,则 ,当且仅当 时等号成立。
证明:令 使得它的补图 具有极大的谱半径。
首先我们来证明 是图G的子图。
假设图G的子图是 ,其中 , 是连接两个圈 和 的路,其中 , 。
如果 ,令
如果 ,令
其中 , 。显然 ,由引理1有 且 ,这与 有极大的谱半径相矛盾,故 ,因此 是图G的子图。
其次我们证明图G只有一个树子图,并且它以G的两个圈唯一的公共点u为根节点。
假设点v是图G的一个树子图 的根节点,其中 并且 。
如果 ,令
如果 ,令
显然 ,由引理1有 且 ,这与 有极大的谱半径相矛盾,因此 。继续上述过程我们可以证得图G只有一个树子图,并且它的根节点为图G的圈上的4度点u。
由引理3很容易证明接在点u出的树是一个星子图。
最后我们证明两个圈 和 都是3长圈。
不失一般性,假设 ,并且 。
如果 ,令
如果 ,令
显然 ,由引理1有 且 ,这与 有极大的谱半径相矛盾,因此 ,同理可证得 。
综上所述,如果 ,要使得 极大,则必有 。 □
定理5若 ,则有 ,其中点u是图G的子图 的3度点,等号成立的充要条件是 。
证明:令 使得它的补图 有极大的谱半径。
首先我们来证明图G只有一个树子图。
假设 和 是图G的两个树子图,它们分别以 上的点u和v为根节点。
如果 ,令
如果 ,令
显然 ,由引理1有 且 ,这与 有极大的谱半径相矛盾,继续上述过程可知图G只含有一个树子图。
由引理3很容易证明接在点u出的树是一个星子图,我们记该树子图的根节点为 。
接下来我们证明 。
假设 ,并且 。
如果 ,令
如果 ,令
显然 ,由引理1有 且 ,这与 有极大的谱半径相矛盾,继续上述过程我们可以得到 ,同理可以证得 , ,由双圈图的定义可知l,p和q最多有一个为1。不失一般性我们令 。因此 。
若 ,则 ,若 ,则 ,如图1所示。
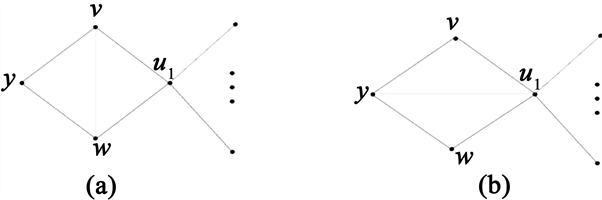
Figure 1. (a) ; (b)
图1. (a) ;(b)
最后我们证明 。
用反证法,假设 ,比较 和 的大小。
如果 ,令
如果 ,令
显然 ,且 和 均与 同构。由引理1有 且 ,这与 有极大的谱半径相矛盾。 □
定理6 假设G是一个n个点的连通的双圈图,则 ,当且仅当 时等号成立。其中 如图1所示。
证明:令v是图G的子图 的4度点,由定理4.2.4和定理4.2.5可知在双圈图中我们只需证明 即可。
令 , 。则有
因为实对称矩阵的特征值非负,所以 。
令 ,则 。
如果 ,则有 ,因此当 时 是个增函数。显然 ,并且
因为 是方程 的一个根,所以 成立。 □
基金项目
新疆自治区研究生创新项目(XJ2021G253)。
文章引用
邱 欢,王 岚,王国平. 双圈图的补图的谱半径
The Spectral Radius of the Complement of Bicyclic Graphs[J]. 理论数学, 2023, 13(06): 1714-1719. https://doi.org/10.12677/PM.2023.136175
参考文献
- 1. Cvertković, D., Doob, M. and Sachs, H. (1980) Spectra of Graphs. Academic Press, New York.
- 2. Cvertković, D. and Rowlinson, P. (1990) The Largest Eigenvalue of a Graph: A Survey. Linear and Multilinear Algebra, 28, 3-33. https://doi.org/10.1080/03081089008818026
- 3. Hong, Y. (1998) Upper Bounds of the Spectral Radius of Graphs in Terms of Genus. Journal of Combinatorial Theory, Series B, 74, 153-159. https://doi.org/10.1006/jctb.1998.1837
- 4. Chang, A., Tian, F. and Yu, A.M. (2004) On the Index of Bicyclic Graphs with Perfect Matchings. Discrete Mathematics, 283, 51-59. https://doi.org/10.1016/j.disc.2004.02.005
- 5. Guo, S.G. (2005) The Spectral Radius of Unicyclic and Bicyclic Graphs with n Vertices and k Pendant Vertices. Linear Algebra and Its Applications, 408, 78-85. https://doi.org/10.1016/j.laa.2005.05.022
- 6. Liu, J. and Zhang, Z. (2010) Spectral Radius of the Complement of Unicyclic Graphs. Journal of East China Normal University (Natural Science), 5, 14-19.
- 7. Horn, R.A. and Johnson, C.R. (1986) Matrix Analysis. Cambridge University Press, Cambridge.
NOTES
*通讯作者。