Computer Science and Application
Vol.
09
No.
07
(
2019
), Article ID:
31406
,
10
pages
10.12677/CSA.2019.97155
Study on Improvement of Dragonfly Algorithm
Xiaoping Hu, Feiwu Zhou*
Engineering Research Center of Advanced Mining Equipment, Ministry of Education, Hunan University of Science and Technology, Xiangtan Hunan

Received: Jul. 4th, 2019; accepted: Jul. 18th, 2019; published: Jul. 25th, 2019

ABSTRACT
An improved dragonfly algorithm (IDA) was proposed to overcome the disadvantages of the standard dragonfly algorithm, such as slow convergence rate and easy to be trapped in local solutions. In order to improve the ability of balancing exploration and exploitation, IDA algorithm proposes two kinds of nonlinear function that can dynamically adjust the convergence factors of the alignment weight and cohesion weight. Grey Wolf mechanism has good performance in exploitation and rate of convergence. In order to improve the convergence accuracy and speed of the dragonfly algorithm, the grey Wolf mechanism was incorporated into the dragonfly algorithm. In the late iteration of the algorithm, the diversity of the population decreases, which makes the algorithm easy to fall into the local solution. The lowliest place elimination series is introduced to improve the diversity of the population and make the algorithm jump out of the local solution. The improved algorithm is simulated with six complex functions and compared with the other three algorithms. The results show that the convergence accuracy, convergence speed and stability of IDA algorithm are better than the other three algorithms.
Keywords:Dragonfly Algorithm, Nonlinear Function, Grey Wolf Mechanism, Lowliest Place Elimination Series
基于蜻蜓算法的改进研究
胡小平,周非无*
湖南科技大学先进矿山装备教育部工程研究中心,湖南 湘潭

收稿日期:2019年7月4日;录用日期:2019年7月18日;发布日期:2019年7月25日

摘 要
针对标准蜻蜓算法中存在的收敛速度慢,易于局部解的缺点,提出一种改进的蜻蜓算法(IDA)。该算法提出两种非线性函数,分别动态调节列队权重和聚集权重的收敛因子,提高算法平衡全局搜索和局部开发的能力;灰狼机制有较强的局部开发能力和收敛速度,融合灰狼机制以提高蜻蜓算法的收敛精度和速度;算法迭代后期种群多样性下降,引入末位淘汰策略来提高种群的多样性,使算法跳出局部解。通过6个复杂的测试函数对改进算法进行仿真,并和其他三个算法进行对比。结果表明,IDA算法的收敛精度、收敛速度和稳定性都优于其他三个算法。
关键词 :蜻蜓算法,非线性函数,灰狼机制,末位淘汰

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
蜻蜓算法(Dragonfly Algorithm)是由Seyedali Mirjalili在2015年提出的一种新兴群智能算法 [1] 。在自然界中,蜻蜓有种独特而罕见的群集行为,蜻蜓聚集只有两个目的:捕猎和迁徙。作者以此为出发点提出两个新的概念:静态和动态。静态(狩猎),群指蜻蜓群体分成多个小群体分布在不同区域进行来回飞行,类似于全局搜索;动态(迁徙),是指蜻蜓形成亚群,并向一个方向长距离迁徙,有利于局部开发。DA算法自提出,因良好的性能引来众多学者的广泛关注。Lang Xu等 [2] 提出用差分进化改进蜻蜓算法并且应用于多级彩色图像分割;Mohamed Abdel-Basset等 [3] 把二进制版的蜻蜓算法(BDA)来解决0~1背包问题, Suresh V等 [4] 利用DA算法求解太阳能静态经济调度问题的方法。Babayigit等 [5] 提出用DA算法实现低旁瓣的CCAAs设计方法。Jafari,Mohammad等 [6] 利用DA算法对具有准三角剖分的正交各向异性无限板进行优化。Mohammed Amroune等 [7] 用蜻蜓算法对电力系统电压稳定进行评估。Gururaghav Raman等 [8] 将蜻蜓算法(DA)应用于光伏系统全局最大功率点(GMPP)跟踪。
虽然该算法有一定的优势,但存在易陷入局部解和收敛速度慢的缺点,针对这些缺点,Sree R. K. S.等 [9] 提出融合粒子群优化算法中的记忆功能,加强蜻蜓个体间的信息交流,以提高算法的收敛精度;Hossam M. Zawbaa等人 [10] 提出基于极值学习机(ELM)的混合蜻蜓算法;Sayed Gehad Ismail [11] 等人提出将混沌映射嵌入到搜索迭代蜻蜓算法中;吴伟民等 [12] 提出加强个体信息交流的算法,增强个体之间的信息交流。
为改善蜻蜓算法容易陷入局部解,收敛速度慢的缺点,本文提两种非线性函数分别动态调节列队和聚集权重的收敛因子,以提高算法的稳定性。将灰狼机制和末位淘汰策略融入到算法当中,改善易于局部解和收敛速度慢的缺点。提出一种有着较强的全局搜索能力和局部开发能力,且能较好的调节全局搜索和局部开发的改进蜻蜓算法(IDA)。
2. 蜻蜓基本算法
Reynoldz [13] 在文章中指出三个关于蜂群体行为准则:分离度、对齐度与聚合度。分离度是指相邻个体间保持适当距离,以免碰撞;对齐度是指速度和方向与相邻个体对齐;聚合度是指个体飞向相邻区域中心。蜻蜓主要目标都是生存,作者Seyedali Mirjalili提出五个因素影响蜻蜓算法的位置更新:分离,列队,聚集,捕食,逃离。数学模型如下:
1) 分离,由公式得:
(1)
X为蜻蜓当前所在位置,Xj表示与X蜻蜓相邻的第j个蜻蜓的位置,N表示与X蜻蜓相邻的个体总数。
2) 列队,由公式得:
(2)
Vj指第j个相邻个体的速度
3) 聚集,由公式得:
(3)
X是当前个体位置。
4) 捕食,指蜻蜓向猎物靠拢,由公式得:
(4)
X+指食物的位置。
5) 逃离,指蜻蜓逃离天敌,由公式得:
(5)
X−指天敌的位置,食物源位置是算法当前最优位置,天敌位置是当前最差的位置。通过以上五种纠正方式的组合形成了蜻蜓的行为,作者通过模仿PSO算法提出步长向量、位置向量来描述蜻蜓的位置。
6) 步长向量更新由公式得:
(6)
Si,Ai,Ci,Fi,Ei指上文的5中纠正方式, 为惯性权重,而s,a,c,f,e分别指的是分离权重,列队权重,聚集权重,捕食权重,天敌权重,t表示当前迭代次数。
7) 位置向量更新由公式得:
当N > 0时 (7)
当N = 0时,利用随机游走(Levy flight)在搜索空间中飞行。
(8)
3. 灰狼算法
灰狼优化算法(GWO) [14] 是一种群智能算法,通过模拟灰狼群的社会等级制度和捕食方式达到优化的目的。灰狼群体社会的统治阶层比较严格,可以分为四个等级:
、
、
、
。灰狼小组的领导者被称为
,为最优解;灰狼等级体系中的第二级是
,为次有解;
可以满足整个群体,为普通狼,保持群体的主导架构,为第四层。第三层是
,第三优解。以
、
、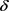 为引导,对目标物进行搜寻。设
为引导,对目标物进行搜寻。设
灰狼种群个数为M,则第i只灰狼在d维度的位置记为 。
在狩猎时,灰狼的位置更新公式如下:
(9)
(10)
(11)
(12)
式中,t为当前迭代次数,A和C为协同系数向量,Xp为猎物的位置,X为灰狼个体的位置。a为A系数的收敛因子, , 表示[0, 1]间的随机数,tmax为最大迭代次数
由于猎物的具体位置未知,可根据灰狼算法中的等级制度,以 、 、 进行引导使狼群接近猎物,灰狼群体可依据 、 、 进行位置更新,公式如下:
(13)
(14)
(15)
(16)
根据(16)对灰狼个体进行更新。
4. 蜻蜓算法的改进
4.1. 非线性调节收敛因子
在前文提到作者把蜻蜓群体运动分为两种状态:静态和动态。静态类似于全局搜索,动态类似于局部探索。为了保证DA算法的收敛性,蜻蜓算法通过调节惯性权重和其他五种权重,使得算法从全局搜索过渡到局部开发。并且,在静态群体中蜻蜓以捕食小型飞行猎物,有较高的聚集权重和较低的列队权重。而在动态群体中,有较低的聚集权重和较高的列队权重 [1] 。标准算法中聚集、列队权重更新方式的数学表达式如下:
(17)
(18)
my_q为列队权重和聚集权重的收敛因子,呈线性变化,当my_q < 0时,my_q = 0, 为为[0, 1]之间的随机数。为了提高算法平衡全局搜索和局部开发的能力,当处于静态群体时赋予高列队权重和较低的聚集权重;在动态群体时应赋予低列队权重和较高的聚集权重。因此提出两种非线性函数动态控制列队和聚集权重的收敛因子,数学表达式如下:
(19)
(20)
Tmax为最大迭代次数,常数b,q为非线性调节系数,t为当前迭代,fmax,fmin分别为a,c取值的上限和下限。当my_qa < 0,my_qc < 0时,则my_qa = 0,my_qc = 0。
用my_qa调节列队权重的收敛因子和用my_qc调节聚集权重的收敛因子。通过两种不同的非线性函数分别调节列队权重和聚集权重的收敛因子,使得算法平衡全局搜索和局部开发的能力得到提高。
4.2. 融合灰狼机制
灰狼算法中的灰狼机制具有结构简单、需要调节的参数少、容易实现的特点,使灰狼机制在局部开发和收敛速度有着良好的性能 [15] [16] [17] 。为提高DA算法的收敛精度和收敛速度,将灰狼机制和蜻蜓算法相结合,即公式(16)。对位置向量更新公式(7)提出改进,公式如下:
(21)
在改进的位置向量更新公式中,包含了个体当前的位置和群体历史最优位置,也包括了蜻蜓算法的步长向量,使得改进后的算法不但融合灰狼机制较强的局部开发能力又能保留了标准DA算法较强的全局搜索能力,并且提高算法的收敛速度。
4.3. 末位淘汰策略
在自然界中适者生存不适者淘汰,鲍义东 [18] 等提出,为了增强狼群的竞争力,引入新的狼,淘汰生存能力较弱的一些狼,以此提高狼群的生存能力。由此受到启发,提出末位淘汰策略来提高算法的多样性。
随着迭代的进行,蜻蜓之间的差异性较小,容易使算法陷入局部解。为了提高算法的多样性,避免陷入局部解,本文引入末位淘汰策略。末位淘汰策略是以蜻蜓个体的适应度值为衡量标准,以适应度值按升序排列,淘汰排在末位的k个蜻蜓个体,同时随机产生k个新的蜻蜓个体,以保持蜻蜓群体数量的稳定。淘汰蜻蜓的个数影响种群的多样性,k值较大时,种群的多样性较大,有利于全局搜索,但不利于算法收敛。k值较小,有利于局部开发。通过对k值大小的控制来保证算法的收敛性。k的值变化如下公式。
(22)
k值为整数,kmax为淘汰的最大值,kmin为淘汰的最小值。
4.4. 算法实现
IMDA具体步骤如下:
步骤1:初始化参数,包括种群大小N、维度d、最大迭代次数Max,五种行为权重和惯性权重,邻域半径;
步骤2:随机初始化位置向量X和步长向量 ;
步骤3:t > 1,更新s, a, c, f, e权重和惯性权重,其中列队权重的收敛因子和聚集权重收敛因子分别由4.1章提出的公式(19) (20)进行更新;
步骤4:计算个体适应度值,更新食物和天敌的位置;
步骤5:利用公式(1)~(5)更新S, A, C, F, E;
步骤6:若存在至少一个相邻个体,则通过(6)公式更新步长向量,用4.2章提出的融合灰狼机制策略更新位置向量,即公式(21)。若不存在相邻个体,则以公式(8)更新位置向量;
步骤7:计算种群个体的适应度值,适应度值以升序排列;
步骤8:用4.3章提出的末位淘汰策略对种群进行淘汰和随机生成。淘汰排在后k位的蜻蜓个体,同时随机生成k个蜻蜓个体;
步骤9:t = t + 1,如果t < Max,返回步骤3。
5. 实验结果及分析
为了进一步验证IDA的优化效果,选取两组具有不同特征的基准测试函数,从不同角度对IDA算法的性能进行基准测试,测试函数分为两组:单模态函数(f1~f4)、多模态函数(f5~f6)。将IDA与标准蜻蜓算法进行对比测试。基准测试函数的具体情况如下表1。
Table 1. Benchmark function test
表1. 基准函数测试
为保证实验的公平性,统一实验环境,实验环境为Windows 7操作系统。所用MATLAB为2016a版本。为了更加合理比较算法的性能,此处选用标准DA算法外还选取了一个改进的蜻蜓算法,差分进化的蜻蜓算法(DEDA) [19] ,遗传算法(GA),GDA是指4.2章提出的融合灰狼机制的蜻蜓算法。分别对6个基准测试函数进行求解。并从最优解、平均解、标准差三个方面对各算法进行评价。共同参数设置:种群规模N = 40,Max = 500。IDA中的fmax = 0.1,fmin = 0,kmax = 0.7 * N,kmin = 0.25 * N差分进化的蜻蜓算法F = 0.5,CR = 0.1。经典遗传算法pc = 0.8,pm = 0.05。由于算法具有随机性,本实验对每个测试函数均运行20次。各算法对6个基准测试函数的计算结果统计如表2所示。
Table 2. Test data of each algorithm
表2. 各算法的测试数据
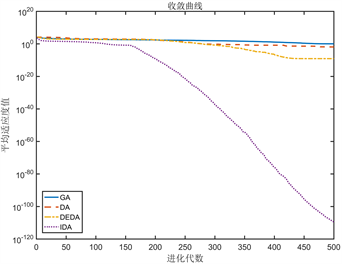
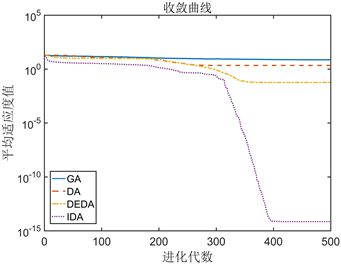
1) 最优解和平均解反应算法的收敛精度,由表2的测试数据可得,GDA算法在求解 TF1~TF4单峰基准测试函数时,寻优能力优于标准蜻蜓算法、GA算法和DEDA算法,对于复杂的多峰的基准测试函数优化效果虽不及单峰基准测试函数,但寻优能力依旧优于标准蜻蜓算法、GA算法和DEDA算法,说明引入灰狼机制有利于提高算法的收敛精度。IDA算法是在GDA算法基础上引入末位淘汰策略,由表2的测试数据可知,无论是单峰基准测试函数还是多峰基准测试函数,IDA的寻优能力优于GDA,说明末位淘汰策略的引入有利于提高算法的多样性,使得算法跳出出局部解。这说明算法经过三方面的改进,使得算法收敛精度和解的整体质量有很大提高,而DA、GA和DEDA都存在过早收敛。
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
 (e)
(e)
 (f)
(f)
Figure 1. Average convergence curves under different test functions. (a) Average convergence curve of TF1 test function; (b) Average convergence curve of TF2 test function; (c) Average convergence curve of TF3 test function; (d) Average convergence curve of TF4 test function; (e) Average convergence curve of TF5 test function; (f) Average convergence curve of TF6 test function
图1. 不同测试函数下的平均收敛曲线图。(a) TF1测试函数的平均收敛曲线图;(b) TF2测试函数的平均收敛曲线图;(c) TF3测试函数的平均收敛曲线图;(d) TF4测试函数的平均收敛曲线图;(e) TF5测试函数的平均收敛曲线图;(f) TF6测试函数的平均收敛曲线图
2) 标准差反应算法的稳定性,对于基准测试函数TF1~TF4来说,IDA比标准函数优化精度分别高出110,61,54,19个数量级。对于多峰函数TF5和TF6的优化效果也分别提高了15和7个数量级,优于其他三个算法,说明改进后的算法在整体上稳定性强,抗“早熟”能力优于其他三个算法。
3) 从图1(a)~(f)可以看出无论是多峰基准测试函数还是单峰基准测试函数,IDA算法的收敛速度比其他三个算法都要快,这说明融合灰狼算法有利于提高算法的收敛速度。
总体来说,无论是对于多峰函数还是单峰函数,相同条件下IDA所得解的质量皆优于其他三个算法。很大程度上改善了标准算法中收敛精度不高、收敛速度慢和易“早熟”的缺点。
6. 结论
针对标准DA算法中的易于陷入局部解、收敛精度低和收敛速度较慢的缺点,本文提出三点改进:基于非线性函数调节列队和聚集权重的收敛因子,提高算法对全局搜索和局部开发的调节能力;融合灰狼机制改进的位置向量,提高算法的收敛精度的同时又能提高算法的收敛速度;末位淘汰策略,淘汰适应度值排在末位的k个蜻蜓个体,同时引入k个新的个体,以此提高了算法的多样性。通过6个基准测试函数仿真结果可知,IDA算法在整体上,函数优化问题的结果优于DA标准算法和其他两个算法。下一步研究目标是应用到机器人路径规划上。
基金项目
国家自然科学基金No. 61572185。
文章引用
胡小平,周非无. 基于蜻蜓算法的改进研究
Study on Improvement of Dragonfly Algorithm[J]. 计算机科学与应用, 2019, 09(07): 1377-1386. https://doi.org/10.12677/CSA.2019.97155
参考文献
- 1. Mirjalili, S. (2016) Dragonfly Algorithm: A New Meta-Heuristic Optimization Technique for Solving Single-Objective, Discrete, and Multi-Objective Problems. Neural Computing and Applications, 27, 1053-1073. https://doi.org/10.1007/s00521-015-1920-1
- 2. Xu, L., Jia, H., Lang, C., et al. (2019) A Novel Method for Multilevel Color Image Segmentation Based on Dragonfly Algorithm and Differential Evolution. IEEE Access. https://doi.org/10.1109/ACCESS.2019.2896673
- 3. Abdel-Basset, M., Luo, Q., Miao, F., et al. (2017) Solving 0-1 Knapsack Problems by Binary Dragonfly Algorithm. In: International Conference on Intelligent Computing, Springer, Cham, 491-502. https://doi.org/10.1007/978-3-319-63315-2_43
- 4. Suresh, V. and Sreejith, S. (2017) Generation Dispatch of Combined Solar Thermal Systems Using Dragonfly Algorithm. Computing, 99, 59-80. https://doi.org/10.1007/s00607-016-0514-9
- 5. Babayigit, B. (2017) Synthesis of Concentric Circular Antenna Arrays Using Dragonfly Algorithm. International Journal of Electronics, 105, 784-793. https://doi.org/10.1080/00207217.2017.1407964
- 6. Jafari, M. and Bayati Chaleshtari, M.H. (2017) Using Dragonfly Algorithm for Optimization of Orthotropic Infinite Plates with a Quasi-Triangular Cut-Out. European Journal of Mechanics A/Solids, 66, 1-14. https://doi.org/10.1016/j.euromechsol.2017.06.003
- 7. Amroune, M., Bouktir, T. and Musirin, I. (2018) Power System Voltage Stability Assessment Using a Hybrid Approach Combining Dragonfly Optimization Algorithm and Support Vector Regression. Ara-bian Journal for Science & Engineering, 43, 3023-3036. https://doi.org/10.1007/s13369-017-3046-5
- 8. Raman, G., Manickam, C., et al. (2016) Dragonfly Algorithm Based Global Maximum Power Point Tracker for Photovoltaic Systems. Advances in Swarm Intelligence, Springer International Publishing, Berlin. https://doi.org/10.1007/978-3-319-41000-5_21
- 9. Sree, R.K.S. and Murugan, S. (2017) Memory Based Hybrid Dragonfly for Numerical Optimization Problems. Expert Systems with Application, 83, 63-78. https://doi.org/10.1016/j.eswa.2017.04.033
- 10. Zawbaa, H.M., Emary, E., Salam, M.A., et al. (2016) A Hybrid Dragonfly Al-gorithm with Extreme Learning Machine for Prediction. International Symposium on Innovations in Intelligent Systems and Applica-tions, Sinaia, 2-5 August 2016.
- 11. Ismail, S.G., Alaa, T. and Ella, H.A. (2018) Chaotic Dragonfly Algorithm: An Improved Me-taheuristic Algorithm for Feature Selection. Applied Intelligence, 49, 188-205.
- 12. 吴伟民, 吴汪洋, 林志毅, 李泽熊, 方典禹. 基于增强个体信息交流的蜻蜓算法[J]. 计算机工程与应用, 2017, 53(4): 10-14.
- 13. Reynolds, C.W. (1987) Flocks, Herds, and Schools: A Distributed Behavioral Model. ACM, New York. https://doi.org/10.1145/37401.37406
- 14. Mirjalili, S., Mirjalili, S.M. and Lewis, A. (2014) Grey Wolf Optimizer. Advances in Engineering Software, 69, 46-61. https://doi.org/10.1016/j.advengsoft.2013.12.007
- 15. Malik, M.R.S., Mohideen, E.R. and Ali, L. (2016) Weighted Distance Grey Wolf Optimizer for Global Optimization Problems. IEEE International Conference on Computational Intelligence & Computing Research, Madurai, 10-12 December 2015. https://doi.org/10.1109/ICCIC.2015.7435714
- 16. Long, W., Liang, X., Cai, S., et al. (2016) A Modified Augmented Lagrangian with Improved Grey Wolf Optimization to Constrained Optimization Problems. Neural Computing and Applications, 28, 1-18. https://doi.org/10.1007/s00521-016-2357-x
- 17. Zhang, S., Luo, Q. and Zhou, Y. (2017) Hybrid Grey Wolf Optimizer Using Elite Opposition-Based Learning Strategy and Simplex Method. International Journal of Computational Intelligence and Applications, 16, Article ID: 1750012. https://doi.org/10.1142/S1469026817500122
- 18. 鲍义东, 夏栋梁, 赵伟艇. 基于凸策略优胜劣汰蚁群算法的机器人路径规划[J]. 计算机系统应用, 2015, 24(8): 122-127.
- 19. 赵齐辉, 杜兆宏, 刘升, 陈思静. 差分进化的蜻蜓算法[J]. 微电子学与计算机, 2018, 35(7): 101-105.
NOTES
*通讯作者。
