Computer Science and Application
Vol.
10
No.
04
(
2020
), Article ID:
35268
,
7
pages
10.12677/CSA.2020.104079
A Hybrid Particle Swarm Optimization for Solving Nash Equilibrium
Huaqin Li
College of Science, Guizhou Institute of Technology, Guiyang Guizhou

Received: Apr. 4th, 2020; accepted: Apr. 19th, 2020; published: Apr. 26th, 2020

ABSTRACT
At present, many intelligent algorithms have been used for solving the Nash equilibrium. They have their own advantages and disadvantages. To overcome local optimum, it designs a hybrid Particle Swarm Optimization for solving Nash equilibrium, by combining the crossover operator in Genetic Algorithm with the basic Particle Swarm Optimization. Experiments show that the algorithm designed is effective, and it is superior to the immune algorithm, immune Particle Swarm Optimization, and basic Particle Swarm Optimization.
Keywords:Nash Equilibrium, Particle Swarm Optimization, Crossover, Hybrid

一种混合粒子群算法求解Nash平衡
黎华琴
贵州理工学院理学院,贵州 贵阳

收稿日期:2020年4月4日;录用日期:2020年4月19日;发布日期:2020年4月26日

摘 要
目前,已有多种智能算法应用于求解Nash平衡,这些算法各有优缺点,为避免粒子群算法在求解Nash平衡时陷入局部最优,本文将遗传算法中的杂交算子引入基本粒子群算法中,设计了一个求解博弈Nash平衡的混合粒子群算法。实验表明,设计的算法具有较好的性能,优于免疫算法,免疫粒子群算法与基本粒子群算法。
关键词 :Nash平衡,粒子群算法,杂交,混合

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
粒子群优化(Particle Swarm Optimization, PSO)算法是由Kennedy和Eberhart于1995年率先提出的,源于对鸟群或鱼群捕食过程的模拟。目前,粒子群优化算法已经在多个领域中得到应用 [1] [2] [3] [4] [5]。
Nash证明了n人非合作博弈Nash平衡的存在性 [6],但迄今未有通用算法来求解所有的博弈模型。Nash平衡的求解,最终可归结为求解一个约束优化问题,要得到此优化问题的准确解通常是很难的。然而在许多实际问题中,我们必须得到此优化问题的一个具体的解。一般采用某些数值方法求其近似,但数值方法通常要求可导、连续等条件。另一类方法是采用智能算法,这些算法直接对结构对象进行操作,不要求可导、连续等条件,它们具有内在的并行性和较好的寻优能力,可以自动调整搜索方向,从而较好地得到优化问题的解。目前,已有多种智能算法用来求解Nash平衡,包括遗传算法 [7]、启发式搜索算法 [8]、免疫算法 [9]、粒子群算法 [5] 及一些改进的粒子群算法 [10] [11] 等。
注意到一方面,求解优化问题时,智能算法后期收敛速度较慢,且容易陷入局部最优;另一方面,粒子群优化算法容易实现,将之作为博弈演化模型,能够比较合理地解释局中人的行为,即局中人是理性的,其目标是最大化自己的收益。本文以粒子群算法为基础,引入遗传算法的杂交算子,设计了一个求解Nash平衡的混合粒子群优化算法。实验表明,本文算法的收敛速度优于目前已有的一些算法。
2. 问题描述
设在一个n人非合作博弈G中,局中人
的纯策略集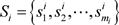 ,其中,
是局中人i的纯策略的个数,局中人i的支付函数为
。称
,其中,
是局中人i的纯策略的个数,局中人i的支付函数为
。称 为局中人i的一个混合策略,其中
为局中人i的一个混合策略,其中
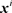 满足
,,即纯策略集
上的一个概率分布。记局中人i的混合策略集记为
。博弈的混合策略组合可记为
。在此混合策略组合下,局中人
的期望支付
。
满足
,,即纯策略集
上的一个概率分布。记局中人i的混合策略集记为
。博弈的混合策略组合可记为
。在此混合策略组合下,局中人
的期望支付
。
定义1 [12] 设
是n人非合作博弈G的一个混合策略组合,如果对任意
及
,均有
,则称
是博弈G的一个混合策略Nash平衡,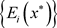 为对应的平衡结果。这里
为对应的平衡结果。这里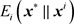 是将局中人i的混合策略
换成混合策略
是将局中人i的混合策略
换成混合策略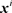 后的期望支付。
后的期望支付。
注意到局中人i的纯策略
等同于混合策略
,其中第k个分量为1,其余分量为0。Nash平衡具备重要性质 [5]: 是n人非合作博弈G的一个混合策略Nash平衡的充要条件是:对于每个局中人i及每个纯策略
,有
。
是n人非合作博弈G的一个混合策略Nash平衡的充要条件是:对于每个局中人i及每个纯策略
,有
。
特别地,对双矩阵博弈 (简记 ),其中, 分别为局中人1与局中人2的混合策略, 是 维支付矩阵,即 与 分别为局中人1采取混合策略 、局中人2采取混合策略 时,局中人1与局中人2的期望支付。
本节余下内容,我们将求解Nash平衡问题转化为优化问题。
我们给每个混合策略组合赋予一个适应度。对混合策略组合
,根据Nash平衡的定义与性质,定义
的适应度
,这里
为局中人i关于混合策略组合
的适应度,
为所有局中人关于混合策略组合
的适应度之和。由Nash平衡的性质,混合策略组合 为纳什均衡解当且仅当适应度函数在
处取得最小值0。故博弈的混合组合空间内只有Nash平衡点的适应度最小。
为纳什均衡解当且仅当适应度函数在
处取得最小值0。故博弈的混合组合空间内只有Nash平衡点的适应度最小。
特别地,对双矩阵博弈 ,其中 是 维支付矩阵, 混合策略组合 的适应度 如下:
其中, 为矩阵A的第i行所对应的向量, 为矩阵B的第j列所对应的向量。
3. 混合粒子群算法设计
在粒子群算法中,优化问题的任一可行解都是搜索空间中的一个粒子,每个粒子都有一个由目标函数所确定的适应度。粒子群算法首先初始化一群随机粒子(包括初始位置及速度),然后这些粒子追随当前的最优粒子在搜索空间中随机搜索,最后通过迭代找到近似最优解 [13]。
每个粒子在搜索时,根据自己的速度、自己搜索到的历史最好点与群体内其他粒子的历史最好点,进行位置与速度的更新。记 为第i个粒子的位置, 为第i个粒子的速度, 为第i个粒子经过的最好点, 为群体内所有的粒子经过的最好点。一般地,粒子的位置和速度都在连续的实数空间内取值。在粒子群算法的迭代中,第i个粒子的速度与位置的更新公式如下:
(1)
(2)
其中,
是第i个粒子在第k次迭代时的速度, 是第i个粒子在第k次迭代时的位置。
是惯性权重,大小决定了对粒子当前速度继承的多少;
是
是第i个粒子在第k次迭代时的位置。
是惯性权重,大小决定了对粒子当前速度继承的多少;
是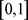 区间内的随机数,
区间内的随机数,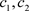 是学习因子。粒子的速度被限制在一个最大速度
的范围内。
是学习因子。粒子的速度被限制在一个最大速度
的范围内。
杂交(交叉)是遗传算法中的一个非常重要的遗传算子,它同时对两个染色体进行操作,组合二者的特性产生新的后代。遗传算法的性能在很大程度上取决于采用的杂交运算的性能。可将杂交算子引入粒子群算法中,基于这一思想,我们设计了一个求解博弈Nash平衡的混合粒子群算法。
在算法中,粒子就是一个混合策略组合,算法如下:
Step 1确定学习因子
,群体规模N,最大迭代代数
,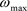 ,
及精确度
。
,
及精确度
。
Step 2随机初始化粒子群及其速度,使每个粒子的第i个向量满足
每个粒子速度的第i个向量满足 。
Step 3计算各个粒子的适应度,并对粒子按照适应度大小进行排序,适应度小的一半粒子直接进入下一代
(另一半记为
),对适应度大的一半粒子进行杂交,杂交之后先对粒子作归一化处理,使之满足
;并与 形成粒子池,计算粒子池中粒子的适应度,选择适应度小的一半粒子与
形成下一代粒子
。
形成粒子池,计算粒子池中粒子的适应度,选择适应度小的一半粒子与
形成下一代粒子
。
Step 4计算当前粒子群 中粒子的适应度值及 , 并把 作为记忆粒子存入记忆库中。
Step 5判断是否满足 或 。 若满足,则停止并输出迭代次数 以及 的适应值;否则,继续。
Step 6利用公式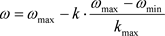 计算惯性权重
。
计算惯性权重
。
Step 7按公式(1)与(2)更新 中粒子的速度与位置。
Step 8依次检验第i个粒子 是否属于 。否则,计算控制步长 (此技术来自文献 [11]),并令 ,然后作归一化处理,使得 回到混合策略组合空间中,形成新一代粒子群体 。然后转到第3步。
关于算法的性能,本文以算法获得Nash平衡或其近似解的平均迭代次数来度量。
4. 数值例子
本文用文献 [9] [10] 中给出的4个经典的 博弈和一个 博弈(例1~5)以及文献 [7] [10] [11] 中共同给出的一个 博弈(例6)作为算例,用本文给出的混合粒子群算法求解这些博弈。
例1 囚徒困境博弈 ,其中, , ;
例2 智猪博弈 ,其中, , ;
例3 猜谜博弈 ,其中, , ;
例4 监察博弈 ,其中, , ;
例5 博弈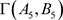 ,其中,
, ;
,其中,
, ;
例6 博弈 ,其中, ,。此博弈具唯一解 。
利用本文设计的混合粒子群算法求解上述博弈,例1~5中算法的参数设置为:群体规模 ,学习因子 ,最大迭代次数为1000,精度设置为 ,其计算结果如表1~5所示。例6中精度设置为 ,其余参数不变,计算结果如表6。
Table 1. Computing result of game Γ ( A 1 , B 1 )
表1. 博弈 的计算结果
Table 2. Computing result of game Γ ( A 2 , B 2 )
表2. 博弈 的计算结果
Table 3. Computing result of game Γ ( A 3 , B 3 )
表3. 博弈 的计算结果
Table 4. Computing result of game Γ ( A 4 , B 4 )
表4. 博弈 的计算结果
Table 5. Computing result of game Γ ( A 5 , B 5 )
表5. 博弈 的计算结果
的计算结果
Table 6. Computing result of game Γ ( A 6 , B 6 )
表6. 博弈 的计算结果
考虑算法的性能,即获得近似解的平均迭代次数。通过计算实验可知,用本文算法在适应函数精度 和群体规模 的情况下,例1~5的5次计算结果分别需要平均迭代2代、3 代、2代、7代和9代。在平均迭代次数方面,优于文献 [10] 用免疫粒子群算法给出的结果(文献 [10] 中例1~5在适应函数精度 的情形下,5次计算结果需要平均迭代7代、3代、4代、14代和15代),特别是例6(本算法在适应度函数精度 )情况下,5次的计算结果需要平均迭代为46,文献 [10] 在适应度函数精度为 ,5次的计算结果需要平均迭288代),本算法有较大的改进,在计算过程中运行速度非常快。当然,本算法也优于 [9] 的算法。
5. 结束语
本文算法的目标在于找到博弈的一个Nash平衡或其近似解。但一个博弈中,可能存在多个Nash平衡,究竟哪个平衡才是最终的博弈结果,本文的算法并没有作这方面的考虑。进一步工作中,我们希望能够引入一些机制,使得算法找到的平衡点更接近与现实的博弈结果。此外,实验还表明,当局中人纯策略数增大时,算法的迭代次数呈指数增长。
致谢
感谢匿名审稿人对本文初稿提出的宝贵意见。
基金项目
贵州省教育厅青年科技人才成长项目(黔教合KY字[2017]225)。
文章引用
黎华琴. 一种混合粒子群算法求解Nash平衡
A Hybrid Particle Swarm Optimization for Solving Nash Equilibrium[J]. 计算机科学与应用, 2020, 10(04): 760-766. https://doi.org/10.12677/CSA.2020.104079
参考文献
- 1. 卿东升, 邓巧玲, 李建军, 刘帅, 刘鑫, 曾素平. 基于粒子群算法的满载需求可拆分车辆路径规划[J]. 控制与决策, 2020, 35(2): 1-9.
- 2. 梁静, 葛士磊, 瞿博阳, 于坤杰. 求解电力系统经济调度问题的改进粒子群优化算法[J]. 控制与决策, 2019, 34(3): 1-10.
- 3. 唐红亮, 吴柏林, 胡旺, 康承旭. 基于粒子群优化的地震应急物资多目标调度算法[J]. 电子与信息学报, 2020, 42(3): 737-745.
- 4. 李倩. 粒子群优化算法在港口船舶物流中的应用[J]. 舰船科学技术, 2020, 42(2): 205-207.
- 5. 余谦, 王先甲. 基于粒子群优化求解纳什均衡的演化算法[J]. 武汉大学学报, 2006, 52(1): 25-29.
- 6. Nash, J. (1951) Non-Cooperative Games. The Annals of Mathematics, 54, 286-295. https://doi.org/10.2307/1969529
- 7. 陈士俊, 孙永广, 吴宗鑫. 一种求解Nash均衡解的遗传算法[J]. 系统工程, 2001(19): 67-70.
- 8. 隗立涛, 修乃华. 基于启发搜索算法的纳什均衡计算[J]. 北京交通大学学报, 2001, 40(33): 87-92.
- 9. 邱中华, 高洁, 朱跃星. 应用免疫算法求解博弈问题[J]. 系统工程学报, 2006, 21(4): 398-404.
- 10. 刘露萍, 贾文生, 蔡江华. 协同免疫量子粒子群算法求非合作博弈Nash平衡[J]. 计算机应用于软件, 2019(8): 203-209.
- 11. 贾文生, 向淑文, 杨剑锋, 等. 基于免疫粒子群算法的非合作博弈Nash均衡问题求解[J]. 计算机应用研究, 2012, 29(1): 28-31.
- 12. 汪贤裕, 肖玉明. 博弈论及其应用[M]. 北京: 科学出版社, 2008: 15-48.
- 13. 汪定伟, 王俊伟, 王洪峰, 等. 智能优化方法[M]. 北京: 高等教育出版社, 2007: 217-252.
