Operations Research and Fuzziology
Vol.
13
No.
03
(
2023
), Article ID:
67083
,
8
pages
10.12677/ORF.2023.133162
一种基于多水平蒙特卡罗方法的最优控制在 金融上的应用
雷鹏
贵州大学数学与统计学院,贵州 贵阳
收稿日期:2023年4月10日;录用日期:2023年6月8日;发布日期:2023年6月15日

摘要
本文使用多水平蒙特卡洛梯度投影优化方法求解一类随机最优控制问题。蒙特卡洛方法,是一种广泛使用的方法,是求解最优控制问题的一种常用方法,但它有自身的局限性,收敛速度慢。我们选取收敛速度较快的多水平蒙特卡洛方法。对这种方法的理论进行分析,之后将该方法用于具体实例,求解金融问题,并通过数值实验验证方法的有效性。
关键词
随机微分方程,最优控制,多水平蒙特卡洛方法,梯度投影,期权定价

Application of Optimal Control Based on Multilevel Monte Carlo Method in Finance
Peng Lei
School of Mathematics and Statistics, Guizhou University, Guiyang Guizhou
Received: Apr. 10th, 2023; accepted: Jun. 8th, 2023; published: Jun. 15th, 2023

ABSTRACT
This paper uses a multi-level Monte Carlo gradient projection optimization method to solve a class of stochastic optimal control problems. Monte Carlo method is a widely used method for solving optimal control problems, but it has its own limitations and slow convergence speed. We selected a multi-level Monte Carlo method with fast convergence speed to analyze the theory of this method, and then applied it to specific examples to solve financial problems. The effectiveness of the method was verified through numerical experiments.
Keywords:Stochastic Differential Equation, Optimal Control, Multilevel Monte Carlo Method, Gradient Projection, Option Pricing

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随机最优控制问题在工程、金融和金融领域得到了广泛的应用,许多学者研究了不同情况下的随机最优控制问题,并将其使用在了求解金融问题。对于随机微分方程,有时候很难找到显式解,因此数值逼近是一个很好的选择。近年来有了一些方法,比如说:有限维随机规划 [1] [2] ,随机最大值原理 [3] ,Bellman动态规划原理 [4] 和鞅方法 [5] ,近年来广泛地应用于数值求解。
金融安全是国家安全的重要体现,当初亚洲金融危机,世界都受其影响,因此对于金融问题的研究很重要,也是国家安全的保障。因此用随机微分方程这一个工具,去研究金融问题,用数值模拟去求解随机微分方程,是本文研究的目的。
蒙特卡洛方法是一种常见的求解随机问题的方法,但收敛速度慢。于是对它加以改进,改进的方法有很多,如多水平蒙特卡洛方法 [6] 和拟蒙特卡洛(QMC)方法 [7] 。对于一个随机微分状态方程,当控制是确定之时,求解随机最优控制问题应当考虑它的不确定性,此时梯度经常包含求期望,多水平蒙特卡洛方法是求解这类问题的一种好方法。
本文将多水平蒙卡洛方法与梯度投影方法相结合,求解随机最优控制问题。为了减少梯度计算带来的统计误差和离散误差的影响,我们使用MLMC方法来估计每次迭代中的梯度,其中的均方误差(MSE)被动态地更新。对这种方法给出理论依据,将金融问题转化为随机最优控制问题,进行数值模拟。
2. 随机最优控制问题
给定一个完全的概率空间 , 是一个实值平方可积的 -适应过程空间,于是有 。 是一维标准布朗运动 生成的自然过滤。定义:
(2.1)
我们给定如下的一个目标函数:
(2.2)
其中h和j都是具有一阶连续导数的光滑函数, 是一个确定性控制, 是一个在控制空间 下的闭凸控制集。 是由如下随机微分方程生成的随机过程:
(2.3)
设f是一个关于 连续可微的函数,g是一个关于 连续可微的函数。可得方程(2.2)存在唯一解 , 。于是函数 是关于 相对应的, 是方程(2.2)的最优解。这个问题称之为随机最优控制问题。
3. 梯度投影方法
函数 , 是(2.2)的解。假设 是一个凸函数,U是一个希尔伯特空间,K是U上的一个闭凸子集。 是一个对称且正定的双线性形式,定义B: 满足 。根据投影运算符 以及一阶优化的必要条件,可以得到
(3.1)
其中 是由 生成的Gateaux导数, 一个正常数 [8] 。
设 , , ,则分段常数空间 可以如下定义:
(3.2)
其中 是 的示性函数。于是公式(3.1)可以做如下的近似计算:
(3.3)
其中 。
为了对(2.1)和(2.2)数值近似求解,我们可以采用下面的迭代公式:
(3.4)
是迭代步长, 是 的数值近似。用下面式子表示 与 之间的误差
(3.5)
于是有如下定理3.1。
定理3.1:若 满足利普西茨条件,并且关于 和 是一直单调的,于是存在正常数c和C满足
(3.6)
(3.7)
(3.8)
(3.9)
假设
时, , (3.10)
对于一些常数 ,我们可选择 ,使得满足
(3.11)
则(3.4)是收敛的。更准确的,我们有
当 时, 。
根据随机最大值原理,可以用下面的修正公式方便地计算目标函数的梯度:
(3.12)
的导数可以由下面式子表示:
根据Riesz表示定理,可得
(3.13)
上述就是梯度投影方法。由于梯度包含期望,因此期望估计的准确性直接影响梯度投影算法的收敛性。通常,它需要大量样本。特别地,当扩散系数 大时样本数量需要更多。因此,我们使用MLMC方法来估计期望。
4. 基于梯度投影的蒙特卡洛方法
我们考虑期望 ,其中 时状态方程和(3.12)的解。我们假设 有连续的导数,通过 作数值近似,在理论分析之前,我们做如下的假设:
H1:y的误差估计满足 。
H2:修正的状态p的误差估计满足 。
H3:对样本估计的计算成本 满足 。
在这假设下我们给出如下的定理。
定理4.1:假设H1和H2成立, ,f和g满足利普西茨连续,则多水平蒙特卡洛法(MLMC)对A的期望误差满足:
(4.1)
定理4.2:假设H1和H2和H3都成立, ,f和g满足利普西茨连续,则通过下面样本数 的选择,可以得到MLMC估计 [7] 。
(4.2)
其中
(4.3)
有 。
当 时,MLMC的总的计算成本 是渐进有界的,如下:
(4.4)
基于梯度投影的MLMC方法的最优控制,它的算法如下:
1) 输入 ,给出迭代误差、初始MSE、最大迭代步长和控制函数。
2) 用MLMC和MSE 去估算梯度 。
3) 用梯度投影(3.4)去更新 。
4) 如果 ,返回 ,开始程序下一步;否则结束。
5) 如果有 或者 成立,决定下一步的MSE 或者 。如果条件不成立,则 。
其中 是2个服从某种确定分布的随机向量,h是离散步长。 是通过这样定义的内积产生的, 。
如果通过上述算法产生的梯度 ,定理3.1的条件都成立,当 时, 由这 决定。我们有(3.4)的基于多水平蒙特卡洛估计是收敛的,于是有
(4.5)
证明:根据(3.8) (3.9)和定理3.1,有
(4.6)
(4.7)
可以得到
(4.8)
其中 , 是(2.2)和(2.3)的精确解。根据上述算法有
(4.9)
我们根据定理有 时, 。
因此可得
.
5. 金融上的应用与数值模拟
随机最优控制问题在工程、金融和金融领域得到了广泛的应用,梯度投影算法下的多水平蒙特卡洛方法可以用在金融问题上,求解金融问题。接下来根据具体问题,实例分析投影梯度下的蒙特卡洛方法的应用,并进行数值模拟。
例子:这个例子来自于金融中的期权定价问题,根据B-S模型 [9] [10] 可得
(5.1)
可将期权定价转化为下面的优化控制问题:
(5.2)
其中 为常数。对这个问题求优化问题可以转化为求解下面的优化控制问题:
(5.3)
最优控制问题的精确解如下:
(5.4)
为了用投影梯度算法下的多水平蒙特卡洛法求解优化控制问题,我们设置以下参数进行数值模拟实验:
。
当MLMC方法被用于估算梯度时,参数 需要被模拟,由于欧拉算法用于数值模拟伴随方程和状态方程,相关参数已经理论上确定了。因此
.
数值实验结果见图1。当 时,实验计算过程的部分信息,见表。
6. 结论
从图1可以知道:当 时,这种算法时收敛的,最终的误差 分别是 。当 时迭代的总时间为 秒。因为我们选择负梯度方向,当 逐步增加时,图中最后一排体现出误差缓慢的增加 。
从表1可以知道:此算法的精度高,用时也比较少,梯度投影下的MLMC能高效准确的数值模拟最优控制问题,为金融中的期权定价问题提供一种好的数值计算方案。
Table 1. Partial information of numerical calculation process (σ = 0.2)
表1. 实验计算过程的部分信息(σ = 0.2)
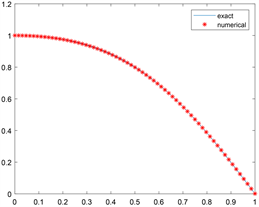
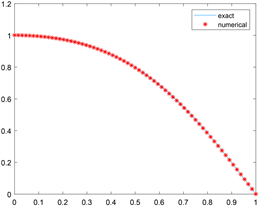

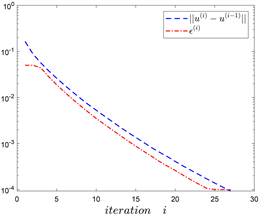
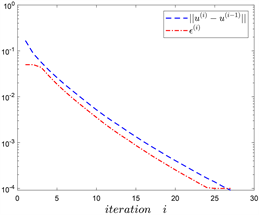
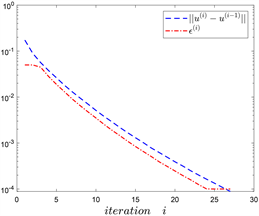
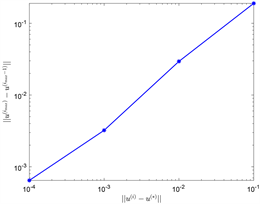
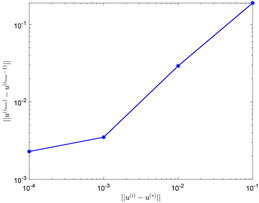
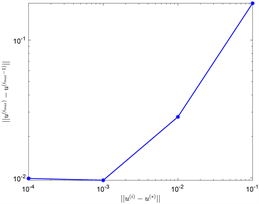
Figure 1. Numerical experimental results (h = 1/64)
图1. 数值实验结果(h = 1/64)
本文讨论了梯度投影下的MLMC的随机最优问题,并将之用于金融问题的实例分析中,数值实验体现了这种方法的高效性和准确性,为分析金融问题提供了一种好的手段。这种方法为求解高维随机最优控制问题提供一种可能,也可以用在随机倒向微分方程上面,也可以求解高维下的期权定价问题。
文章引用
雷 鹏. 一种基于多水平蒙特卡罗方法的最优控制在金融上的应用
Application of Optimal Control Based on Multilevel Monte Carlo Method in Finance[J]. 运筹与模糊学, 2023, 13(03): 1610-1617. https://doi.org/10.12677/ORF.2023.133162
参考文献
- 1. Heitsch, H. and Romisch, W. (2003) Scenario Reduction Algorithms in Stochastic Programming. Computational Optimization and Applications, 24, 187-206.
- 2. Raffard, R., Hu, J. and Tomlin, C. (2005) Adjoint-Based Optimal Control of the Expected Exit Time for Stochastic Hybrid Systems. In: Morari, M. and Thiele, L., Eds., Hybrid Systems: Computation and Control, Lecture Notes in Computer Science, Vol. 3414, Springer-Verlag, Berlin. https://doi.org/10.1007/978-3-540-31954-2_36
- 3. Archibald, R., Bao, F., Yong, J. and Zhou, T. (2020) An Efficient Numerical Algorithm for Solving Data Driven Feedback Control Problems. Journal of Scientific Computing, 85, Article Number: 51. https://doi.org/10.1007/s10915-020-01358-y
- 4. Kushner, H.J. and Dupuis, P. (2001) Numerical Methods for Stochastic Control Problems in Continuous Time. 2nd Edition, Springer-Verlag, New York. https://doi.org/10.1007/978-1-4613-0007-6
- 5. Korn, R. and Kraft, H. (2001) A Stochastic Control Approach to Portfolio Problems with Stochastic Interest Rates. SIAM Journal on Control and Optimization, 40, 1250-1269. https://doi.org/10.1137/S0363012900377791
- 6. Giles, M.B. (2015) Multilevel Monte Carlo Methods. Acta Numerica, 24, 259-328. https://doi.org/10.1017/S096249291500001X
- 7. 谢非. 资产定价与数据科学中的拟蒙特卡洛方法[D]: [硕士学位论文]. 北京: 清华大学, 2019.
- 8. Gong, B., Liu, W., Tang, T., et al. (2017) An Efficient Gradient Pro-jection Method for Stochastic Optimal Control Problems. SIAM Journal on Numerical Analysis, 55, 2982-3005. https://doi.org/10.1137/17M1123559
- 9. 姜礼尚. 期权定价的数学模型与方法[M]. 北京: 高等教育出版社, 2008.
- 10. 蒲兴成, 张毅. 随机微分方程及其在数理金融中的应用[M]. 北京: 科学出版社, 2010.
