Statistics and Application
Vol.07 No.02(2018), Article ID:24681,9
pages
10.12677/SA.2018.72029
Application of Hierarchical Bayesian Model Based on Gibbs Sampling in Statistical Inference of Fire Occurrences
Kang Cao
Shanghai Maritime University, Shanghai

Received: Apr. 3rd, 2018; accepted: Apr. 21st, 2018; published: Apr. 28th, 2018

ABSTRACT
Gibbs sampling method is the most widely used method in MCMC algorithm. The basic idea of Gibbs sampling is to construct the Markov chain by the conditional distribution family of the components of the parameter vector when the high-dimensional parameters are posteriorly inferred, so that its invariant distribution is the target distribution. This topic is based on the method to determine the parameters of the model, which can be based on existing information to estimate the number of years, the number of fire occurred in the region and the estimated confidence interval of the parameters.
Keywords:Gibbs Sampling, Hierarchical Bayesian Model, Markov Chain, Fire
基于Gibbs抽样的分层贝叶斯模型在火灾发生次数统计推断中的应用
曹康
上海海事大学,上海

收稿日期:2018年4月3日;录用日期:2018年4月21日;发布日期:2018年4月28日

摘 要
Gibbs抽样是MCMC抽样算法中应用最广泛的方法之一,其核心思想是对高维参数进行后验推断时,通过参数向量的分量的条件分布族来构造Markov链,使其不变分布为目标分布。本文利用Gibbs抽样方法结合分层贝叶斯模型,对我国各地区火灾发生次数进行了回测,结果显示,相比于传统的poisson分布刻画方法,基于Gibbs抽样的分层贝叶斯方法充分利用了历史信息使结果更具可信度。
关键词 :Gibbs抽样,分层贝叶斯模型,马尔科夫链,火灾

Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近年来,由于我国在城镇化进程中的快速推进,城市规模和人口越来越多,因此而产生的城市问题也越来越多,火灾即是其中之一。据公安部消防局公布的数据,2016年全国共接报火灾31.2万起,造成死亡1582人,伤1065,直接财产损失37.2亿元。可见,火灾对市民人身和财产安全造成了巨大的危害,如何寻找出火灾易发区域,采取有效措施及时防范已是一项十分艰巨和重要的任务。
影响火灾发生率的因素有很多,如Schaeman [1] (1997)认为经济越发达的地区,火灾发生次数可能越少;同样,杨立中 [2] (2003)也研究得出经济水平欠发达地区发生火灾的次数相应也较高。此外,也有很多学者也关注于对火灾影响因素进行量化分析,如邓欧 [3] (2012)等建立了Logistic全局火灾预报回归模型;Bisquert [4] 等(2012)利用人工神经网络对火灾发生率进行建模;Dlamini [5] (2011)也建立了基于贝叶斯网络的火灾发生率模型。总的来说,目前已有研究中无论是Logistic回归、人工神经网络还是贝叶斯都关注的是传统影响因素下模型精度的问题,对火灾发生率的空间分布考虑较少。
本文即是在此背景下,从统计抽样的角度,利用贝叶斯思想,建立分层贝叶斯模型,再利用Gibbs抽样方法得到不同地区火灾发生次数的Markov链,借此分析了不同地区火灾发生次数的分布特点。
2. 分层贝叶斯模型
分层贝叶斯模型 [6] 是贝叶斯模型的一种,用来为具有不同水平的问题进行建模,通过贝叶斯方法估计后验分布的参数。很多时候模型会具有多个参数,这些参数也有可能具有结构性的联系。例如在研究第i次射击命中10环的概率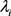 ,很显然我们预估
,很显然我们预估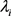 是相互联系的,利用贝叶斯方法,将
是相互联系的,利用贝叶斯方法,将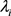 看做总体分布的一个样本,观测数据
看做总体分布的一个样本,观测数据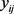 ,其中j为第j次试验,利用观测数据可以用来估计
,其中j为第j次试验,利用观测数据可以用来估计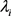 的分布。这样就构成了一个分层的贝叶斯模型。分层贝叶斯模型是通过计算参数在已知观恶量下的条件后验概率,推到过程为:
的分布。这样就构成了一个分层的贝叶斯模型。分层贝叶斯模型是通过计算参数在已知观恶量下的条件后验概率,推到过程为:
1) 写出联合后验密度p(θ,φ|y),其非正规化的形式是超先验分布p(φ)、总体分布p(θ|φ)和似然函数p(y|θ)的乘积。
2) 在给定超参数φ的情况下,确定θ的条件后验密度,固定观测值y的情况下,它是φ的函数p(θ|φ, y)。
3) 使用贝叶斯分析范例估计φ,也就是要获取边缘后验分布p(φ|y)。
3. Gibbs抽样
3.1. Gibbs抽样原理
Gibbs抽样 [7] 简单、应用最广泛的MCMC抽样方法之一,应用该抽样方法的前提是要分布π(x)的满条件分布已知,即对于任意i,在已知x的第i个分量以外其他分量值的条件下,第i个分量的条件分布
已知。在给定初值点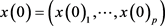 后,假定第t次迭代值为x(t),则第t + 1次迭代分为如下p步(这里p表示x共有p个分量)。具体算法为:
后,假定第t次迭代值为x(t),则第t + 1次迭代分为如下p步(这里p表示x共有p个分量)。具体算法为:
给定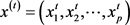 ,
,
(1) 生成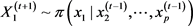 ,
,
···
(i) 生成 ,
,
···
(p) 生成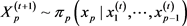
3.2. Gibbs抽样的具体实现方法
设 是p维参数向量,
是p维参数向量,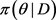 是观察到数据集D后θ的后验分布。Gibbs抽样方法 [8] 如下:
是观察到数据集D后θ的后验分布。Gibbs抽样方法 [8] 如下:
第0步.任意选取一个初始点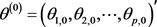 ,并置
,并置 ;
;
第1步.按下列方法生成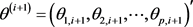 :
:
生成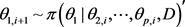 ,
,
生成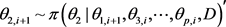 ,
,
···
生成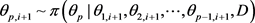 ;
;
第2步。置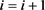 ,并返回到第1步.
,并返回到第1步.
在这个算法过程中,θ的每一个分量按照自然顺序生成,每一个循环需要生成p个随机变量。
4. 应用实例
4.1. 案例介绍
本文根据2012年全国各地区发生火灾的次数(见表1,数据来源于公安部消防局中国火灾消防统计年鉴)为样本,使用分层贝叶斯方法对各地区的火灾发生次数进行统计推断,具体数据如表1所示。
4.2. 模型建立
假设第i地区发生火灾的次数服从参数为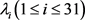 的poisson分布。对于观察时间
的poisson分布。对于观察时间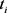 ,发生火灾次数
,发生火灾次数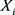 服从参数为
服从参数为 的poisson分布
的poisson分布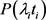 。考虑到gamma分布是poisson分布和gamma分布的共轭先验分布,故取参数
。考虑到gamma分布是poisson分布和gamma分布的共轭先验分布,故取参数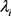 和β服从gamma分布。综上,考虑下列分层贝叶斯模型:
和β服从gamma分布。综上,考虑下列分层贝叶斯模型:
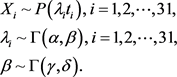
则,各层的条件密度分别为:
Table 1. Number of fire occurrences by region in 2012
表1. 2012年各地区火灾发生次数数据
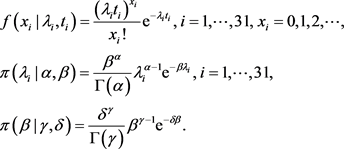
参数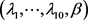 联合后验分布为:
联合后验分布为:
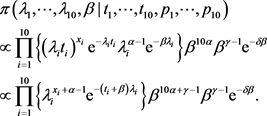
各参数的全条件后验分布为:
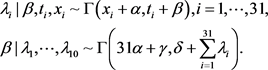
4.3. 算法的实现与结果
该Gibbs抽样是直接从各参数的全条件后验中进行抽样的,取超参数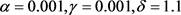 ,进行10,000次迭代,结果见图1、图2 (由于地区较多,这里只给出了表1中的前10个地区的λ及β)。
,进行10,000次迭代,结果见图1、图2 (由于地区较多,这里只给出了表1中的前10个地区的λ及β)。
由上可以看出参数大部分都是在迭代2000次后趋于稳定,故将前2000次作为预迭代剔除出去,得到的结果见图3。
剔除前2000次最后得到的参数估计值(均值)及95%置信区间见表2。
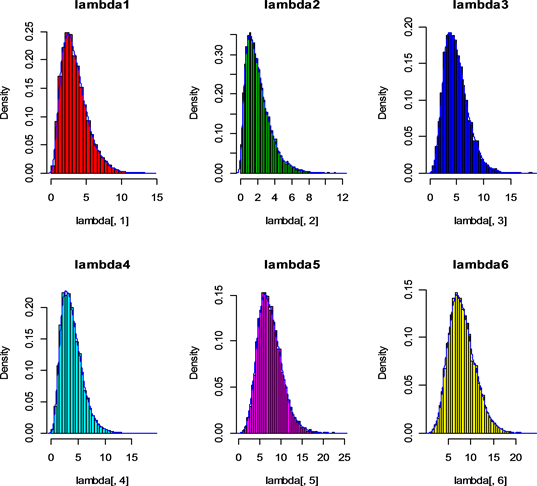
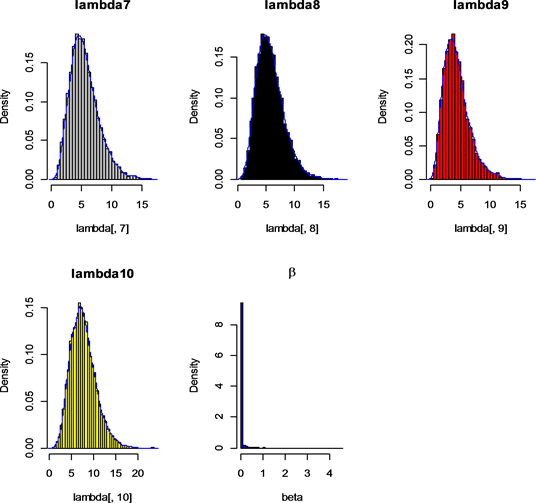
Figure 1. Some parameters posterior histogram and density curve
图1. 部分参数后验直方图和密度曲线图

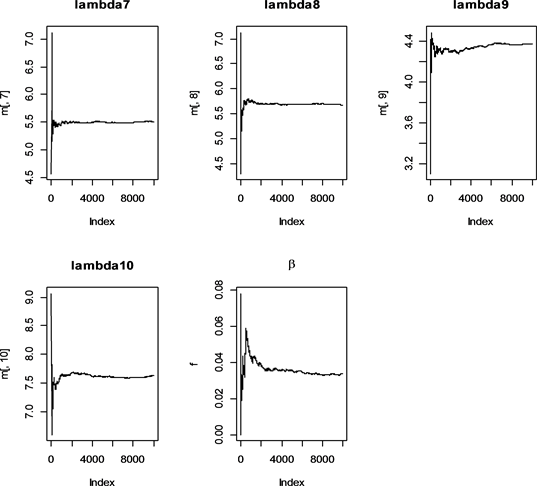
Figure 2. Iterate over 10,000 times the dynamic average of some parameters
图2. 迭代10,000次的部分参数的动态均值
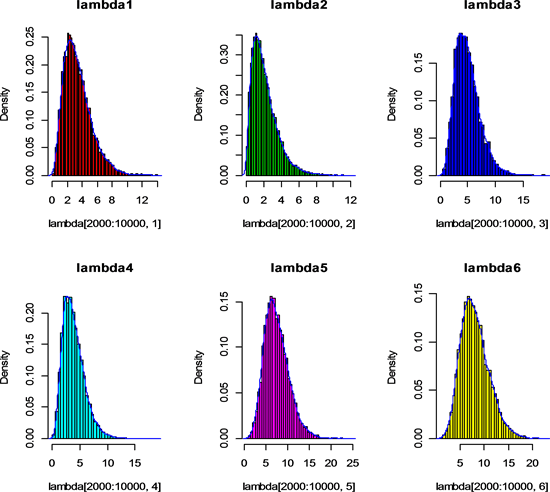
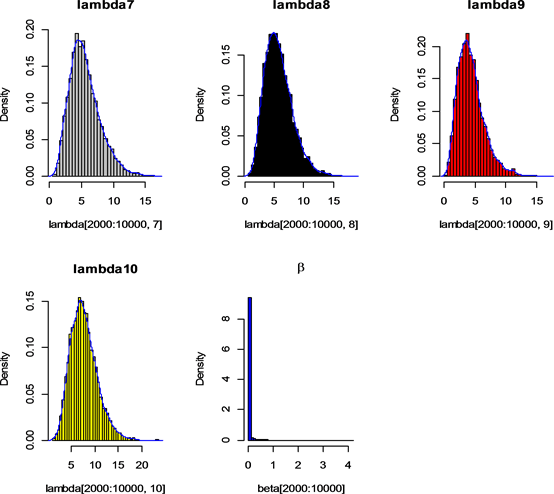
Figure 3. Remove the first 2000 posterior histograms and density plots
图3. 剔除前2000次的后验直方图和密度曲线图
Table 2. Parameter confidence interval
表2. 参数置信区间
5. 结论
以上得到了31个地区的λ、β及其95%置信区间。在此基础上可对2012年以后火灾发生次数进行统
计推断。以北京地区为例,其火灾发生次数xi概率为 。计算北京地
。计算北京地
区2013发生1千次火灾的概率为c由于火灾发生次数数据的不可重复性,传统经典统计方法在样本量较小的情形下很难得到具有说服力的结论,而贝叶斯方法充分利用了历史数据中所包含的信息,通过Gibbs抽样,可推断下一期的火灾发生次数的概率,为消防部门的工作安排提供理论指导,具有很强的实际意义。
文章引用
曹康. 基于Gibbs抽样的分层贝叶斯模型在火灾发生次数统计推断中的应用
Application of Hierarchical Bayesian Model Based on Gibbs Sampling in Statistical Inference of Fire Occurrences[J]. 统计学与应用, 2018, 07(02): 247-255. https://doi.org/10.12677/SA.2018.72029
参考文献
- 1. Schaenman, P.S., Hall, J. and Schainblatt, A. (1977) Procedures for Improving the Measurement of Local Fire Protection Effectiveness.
- 2. 杨立中, 江大白. 中国火灾与社会经济因素的关系[J]. 中国工程科学, 2003, 5(2): 62-67.
- 3. 邓欧, 李亦秋, 冯仲科, 张冬有. 基于空间Logistic的黑龙江省林火风险模型与火险区划[J]. 农业工程学报, 2012, 28(8): 200-205.
- 4. Bisquert, M., Caselles, E., Sánchez, J.M., et al. (2012) Application of Artificial Neural Networks and Logistic Regression to the Prediction of Forest Fire Danger in Galicia Using MODIS Data. International Journal of Wildland Fire, 21, 1025-1029. https://doi.org/10.1071/wf11105
- 5. Dlamini, W.M. (2011) Application of Bayesian Networks for Fire Risk Mapping Using GIS and Remote Sensing Data. Geojournal, 76, 283-296. https://doi.org/10.1007/s10708-010-9362-x
- 6. 王宁. 基于分层贝叶斯分析的城镇登记失业率估计方法[D]: [硕士学位论文]. 天津: 天津财经学, 2012
- 7. 张颖, 傅强. GJR-CAViaR模型的贝叶斯分位数回归——基于Gibbs抽样MCMC算法实现[J]. 中央财经大学学报, 2017(7): 87-95.
- 8. 马跃渊, 徐勇勇. Gibbs抽样算法及软件设计的初步研究[J]. 计算机应用与软件, 2005(2): 124-126.
