Advances in Applied Mathematics
Vol.05 No.03(2016), Article ID:18448,15
pages
10.12677/AAM.2016.53058
Distributed Strategies for Group-Balancing General Weighted Directed/Undirected Graphs
Fan Yang1, Junyan Yu1, Yulan Gao2, Mei Yu3, Jinliang Shao1
1School of Mathematical Sciences, University of Electronic Science and Technology of China, Chengdu Sichuan
2National Key Laboratory of Science and Technology on Communications, University of Electronic Science and Technology of China, Chengdu Sichuan
3School of Electrical and Electronic Engineering, North China Electric Power University, Beijing

Received: Aug. 17th, 2016; accepted: Aug. 27th, 2016; published: Aug. 30th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
A key problem of solving the consensus coordination control of multi-agent systems is to design appropriate protocols or algorithms which guarantee the agents reaching consensus. Although existing theoretical results have illustrated the balance conditions and the group-balance conditions are necessary when it comes to average consensus and group average consensus respectively, there are few results on how to balance and group-balance a general graph. In this paper, we design two distributed algorithm to group-balance directed and undirected graphs respectively, and prove the validity of the algorithms via both theoretical analysis and example illustrations.
Keywords:Multi-Agent Systems, Group Consensus, Distributed Algorithms, Group-Balance, Directed/Undirected Graphs

群平衡化赋权有向图/无向图的分布式算法研究
杨繁1,于俊燕1,高玉兰2,禹梅3,邵晋梁1
1电子科技大学,数学科学学院,四川 成都
2电子科技大学,通信抗干扰技术国际级重点实验室,四川 成都
3华北电力大学,控制与计算机工程学院,北京

收稿日期:2016年8月17日;录用日期:2016年8月27日;发布日期:2016年8月30日

摘 要
解决多智能体系统一致性协调控制的关键问题是设计合适的协议或算法使得多智能体的状态最终达到一致。己有的理论结果说明一些图平衡条件,如平衡条件和群平衡条件,是解决多智能体系统平均一致性问题和群平均一致性问题的一个必要条件。因此怎样平衡化和群平衡化一个一般图是一个值得研究的问题。然而目前涉及到如何平衡化和群平衡化一个一般图的结果还很少。本文针对有向拓扑图和无向拓扑图,分别提出两种不同的群平衡化算法,并从理论分析和数值仿真两方面验证两种算法的有效性。
关键词 :多智能体系统,群一致性,分布式算法,群平衡,有向/无向图

1. 引言
多智能体系统是由许多相互关联的个体通过局部规则组成的系统,其控制理论在过去的十几年中引起诸多学者关注,并得到了快速发展。由于多智能体控制是通过协调控制多智能体系统每个个体,最终达到解决大型、复杂的问题,这一系统特点使得多智能体系统在工程上的潜在应用价值得到了不同学科领域学者的广泛关注,例如:多机器人/车辆系统、传感器网络、人造卫星簇等。
作为多智能体协调控制的基本问题,一致性问题得到广泛关注,己涌现出很多优秀成熟的结果 [1] [2] 。Olfati-Saber在 [1] 中研究了固定/切换拓扑下一致性问题,确立了一致性问题研究的基本理论框架。随后,更深入的结果和有效的方法不断被提出 [3] - [17] 。其中基于图理论Ren和Beard [3] 得到了固定拓扑下一阶线性多智能体系统达到一致性的充要条件是系统的拓扑图包含生成树;切换拓扑下,若在给定长度的时间区间上的并包含生成树,则系统能实现状态一致。在文献 [5] - [8] 中,作者运用代数思想解决了离散时间多智能体系统一致性问题的充要条件,并基于Lyapunov稳定性理论解决了连续时间多智能系统的一致性问题。随着对一致性问题研究的深入,二阶多智能体系统作为一种更一般的模型也得到了不同学科的关注 [9] - [12] 。在 [10] 中作者运用代数理论分析系统方程的特征根得到了系统达到一致的充要条件,并指出拓扑结构包含生成树只是二阶系统达到一致的必要条件而非充分条件。文献 [11] 研究切换拓扑下具有时滞的二阶离散多智能体系统的一致性问题,利用模型变换(增广系统)和非负矩阵理论,作者给出了在有联合生成树的情形下一致性问题可解的充分条件。
对于一般的多智能体一致性问题,最终所有个体的状态渐近收敛到同一个值。但是很多情况下,由于个体性能的差异或者任务分配的不同,多智能体系统的个体被分成不同的群体,针对这样的复杂多智能体网络, [18] - [25] 研究了比较广泛的一致性——群一致性。对于多智能体群一致性问题,一个关键问题是设计合适的协议和算法使被分为多个群的图的图中相同群内个体达到相同状态而不同群内的个体状态最终可以不尽相同。对于一阶连续时间多智能体系统,在文献 [18] - [20] 中作者给出了定常拓扑和切换拓扑下群平均一致性可解的条件。值得注意的是文中增加了平衡对这一条件用以限制群之间的藕合作用。随后,关于多智能体系统两个群的一致性问题,在文献 [25] 中,作者给出了弱于 [18] 的有向图能达到群一致性的充分条件,即对于每一个群,群内每个点对于另一个群的邻接出权值在任何时间都是相同的群平衡条件。
基于以上分析,可以看到,当涉及平均一致性和群平均一致性时,平衡条件和群平衡条件是必需的。因此,对于多智能体系统的平均一致性和群平均一致性问题,如何平衡化(群平衡化)一个一般图让它满足平衡条件(群平衡条件)成为一个待解决的关键问题。近几年,基于平均一致性平衡条件己有一些有趣的结果被提出来。文献 [26] 中提供了平衡化一个赋权有向图的两个算法,它用迭代条件去改变某些权值,最终达到每个点的出权值之和等于它的入权值之和的平衡条件。在初始拓扑图是强连通的(或强连通并图)的条件下,文献 [27] 中提出了一个分布式迭代算法,通过给每个边设计一个正整数边权,使得拓扑图达到平衡。文献 [28] 中提出了一个分散式算法去平衡化一个强连通赋权图,其特点是依赖于Laplacian的零特征值的左特征向量的分布式估计。文献 [29] 中作者证明了只要一个有向图的关联矩阵的零空间包含正向量,这个有向图就能被平衡。
然而,多智能体系统问题中图往往被用来描述个体或群体之间的信息交流模式,因而实际的模型可以很复杂,从而对图的要求也不仅仅局限于一个图的内部的特性。一个很好的例子就是群一致性问题,该问题就对两个或两个以上图之间的连接有一定的要求。然而目前关于平衡化的结果均只涉及到一个图的平衡,而没有考虑两个或更多图之间的信息。在此背景下,本文以含有两个群的多智能体系统为研究对象,以代数图理论为主要分析工具,设计分布式群平衡化算法。本文的主要贡献是设计了两种算法分别对应于赋权有向图和赋权无向图。由于两种算法初始条件对图本身无任何要求,从而基于这两种算法,一般的拓扑图最终达到群平衡,从而为分布式多智能体系统达到群平均一致提供必要条件。本文的结构如下:第2节为问题描述和基础理论;第3、4节分别给出赋权有向图和赋权无向图的群平衡算法描述、算法收敛性分析和算例;第5节是本文小结。
2. 图理论及准备工作
令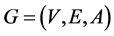 是由
是由 个顶点组成的赋权有向图,其中点集表示为
个顶点组成的赋权有向图,其中点集表示为 ,边集表示为
,边集表示为 ,一个赋权邻接矩阵表示为
,一个赋权邻接矩阵表示为 ,其中
,其中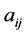 为实数。点指标集
为实数。点指标集 属于一个有限集,
属于一个有限集, 的一条边表示为
的一条边表示为 (从
(从 到
到 )。图的边权值是实数,即
)。图的边权值是实数,即 而且,我们假设对所有
而且,我们假设对所有 ,有
,有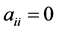 。
。
不失一般性,本文考虑由 个节点组成的网络
个节点组成的网络 ,
, 是一个赋权有向图
是一个赋权有向图 ,
,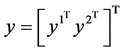 ,
, ,
,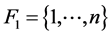 ,
, ,
, ,
,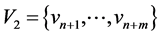 ,则
,则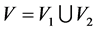 ,
,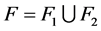 。
。 ,
, ,目标是设计算法使得
,目标是设计算法使得 ,
,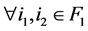 ,
,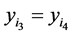 ,
, (群平衡条件)。定义
(群平衡条件)。定义 ,其中
,其中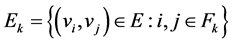 ,
,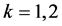 。赋权邻接矩阵
。赋权邻接矩阵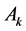 依附于
依附于 。则
。则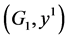 和
和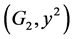 是
是 的两个子网络。因此,网络
的两个子网络。因此,网络 是由两个子网络
是由两个子网络 和
和 组成的。
组成的。
本文的目标是通过设计算法实现一个一般的图的群平衡,即设计有效的算法达到群平衡化一个任意图的目的。这里考虑的平衡是 [25] 为了实现多智能体的群一致性而提出的群平衡条件,具体地,群平衡条
件数学表达式如下:满足群平衡条件 [25] :1)  2)
2) 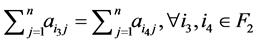 。该条件表明:对于每一群组(子图),群(子图)中每个个体(结点)接受另一个群(子图)的综合影响(邻接出权值)在任何时间都相同。
。该条件表明:对于每一群组(子图),群(子图)中每个个体(结点)接受另一个群(子图)的综合影响(邻接出权值)在任何时间都相同。
3. 赋权有向图的群平衡化算法
由于多智能体系统群一致性研究多智能体渐近达到两个以上的最终状态,因此个体往往有两个或两个以上的分组,每一组的个体渐近达到一致。这导致拓扑图往往按照个体的分组被分成两个或两个以上的子图。我们针对群一致的拓扑特性设计两种分布式算法,使得一个一般的图在有限步满足群平衡条件。由于设计的算法对初始图没有限定,因此这一节设计的算法可以应用到任何一个一般的图上,最终实现该图的群平衡。
含有两个子图的赋权有向图的群平衡化
A. 算法I
输入对象:一个有 个点的赋权有向图
个点的赋权有向图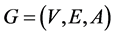 ,它包含两个子图,分别是有
,它包含两个子图,分别是有 个点的赋权有向图
个点的赋权有向图 和有
和有 个点的赋权有向图
个点的赋权有向图 。
。
初始化: ,如果
,如果 ,则
,则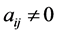 ,否则
,否则 。
。
迭代:1) 对于每个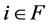 ,计算
,计算

如果对于任意的 ,有
,有 ,则群平衡条件达到,退出算法。
,则群平衡条件达到,退出算法。
2) 计算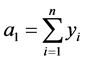 (
(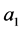 为
为 中所有点的群外邻接出权值和),
中所有点的群外邻接出权值和), (
(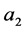 为
为 中所有点的群外邻接出权值和)。如果
中所有点的群外邻接出权值和)。如果 且
且 ,转3);如果
,转3);如果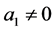 或
或 ,转4)。
,转4)。
3) 由 ,
, 知,对于每个群,群内所有点的群外邻接出权值之和为零,如果群内每个点的群外邻接出权值都为零,则群内每个点的群外邻接出权值相等,平衡条件达到。为了达到此目的设计了(i)~(iii)。
知,对于每个群,群内所有点的群外邻接出权值之和为零,如果群内每个点的群外邻接出权值都为零,则群内每个点的群外邻接出权值相等,平衡条件达到。为了达到此目的设计了(i)~(iii)。
(i) 在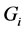 中选择有最大
中选择有最大 值的点
值的点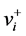 ,它的
,它的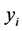 值表示为
值表示为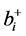 ,在
,在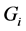 中选择有最小值的点
中选择有最小值的点 。
。
(ii) 找到 的其中一条出边
的其中一条出边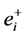 和
和 的其中一条出边
的其中一条出边 ,
, 的权值减去
的权值减去 ,
, 的权值加上
的权值加上 。
。
(iii) 置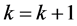 ,转1)并重复以上迭代。
,转1)并重复以上迭代。
4) 以下(i)~(ii)为 与
与 重新赋值。因为某个群中可能存在没有群外出邻居的点(点
重新赋值。因为某个群中可能存在没有群外出邻居的点(点 的群外出邻居是指与点
的群外出邻居是指与点 的出边相关联并且与点
的出边相关联并且与点 不在同一个群内的点),这样的点群外邻接出权值只能是零。在此情况下,要使此群内每个点的群外邻接出权值相等,则此群内所有点的群外邻接出权值之和必需为零。若图中每个点都有群外出邻居,假设在
不在同一个群内的点),这样的点群外邻接出权值只能是零。在此情况下,要使此群内每个点的群外邻接出权值相等,则此群内所有点的群外邻接出权值之和必需为零。若图中每个点都有群外出邻居,假设在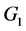 中有
中有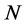 个点,在
个点,在 中有
中有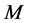 个点。如果群
个点。如果群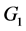 内每个点的群外邻接
内每个点的群外邻接
出权值都为 ,
, 群内每个点的群外邻接出权值都为
群内每个点的群外邻接出权值都为 ,则对于每个群,群内每个点的群外邻接出权
,则对于每个群,群内每个点的群外邻接出权
值相等,为了便于此条件下的有向图的群平衡化,(iii)中定义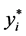 作为
作为 值与目的值的偏差,只要使每个点的
值与目的值的偏差,只要使每个点的 值都为零就达到了群平衡条件。以下为算法的具体步骤:
值都为零就达到了群平衡条件。以下为算法的具体步骤:
(i) 如果 ,若
,若 中存在没有群外出邻居的点,让
中存在没有群外出邻居的点,让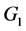 中某一点的某一出边的边权值减
中某一点的某一出边的边权值减 ,重新计算
,重新计算 ,则
,则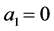 ;若
;若 中每个点至少有一个群外出邻居,则
中每个点至少有一个群外出邻居,则 。
。
(ii) 如果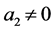 ,若
,若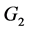 中存在没有群外出邻居的点,让
中存在没有群外出邻居的点,让 中某一点的某一出边的边权值减
中某一点的某一出边的边权值减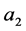 ,重新计算
,重新计算 ,则
,则 。若此时
。若此时 ,算法转3);若
,算法转3);若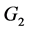 中每个点至少有一个群外出邻居,则
中每个点至少有一个群外出邻居,则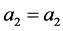 。
。
(iii) 令 ,
, ,如果对任意
,如果对任意 ,有
,有 ,此时
,此时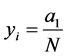 ,
, ,
, ,
, ,满足平衡条件(1)和(2),则图达到群平衡,退出算法。
,满足平衡条件(1)和(2),则图达到群平衡,退出算法。
以下(iv)~(vi)中与3)中的方法类似。
(iv) 在 中选择有最大
中选择有最大 值的点
值的点 ,它的
,它的 值表示为
值表示为 ,在
,在 中选择有最小值
中选择有最小值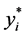 的点
的点 ;
;
(v) 找到 的其中一条出边
的其中一条出边 和
和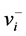 的其中一条出边
的其中一条出边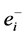 ,
, 的权值减去
的权值减去 ,
, 的权值加上
的权值加上
(vi) 置 ,转1) 并重复以上迭代。
,转1) 并重复以上迭代。
为了更直接地理解上述算法,请看下面一个例子。
例1:考虑赋权有向图图1。 ,其中
,其中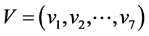 ,
, ,
,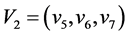 ,
,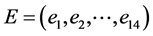 ,
, 。假设
。假设 ,
, ,
,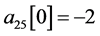 ,
,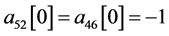 。
。
计算
 ,
,
 ,
,
因为 中每个点至少有一个群外出邻居,所以转4)-(iii),
中每个点至少有一个群外出邻居,所以转4)-(iii),
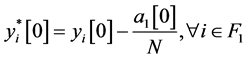 ,
,
算法演示(见图1)。
一旦计算出每个点的 值,转入算法(4)-iv):选择每个群中具有最大
值,转入算法(4)-iv):选择每个群中具有最大 值的点,如
值的点,如 中的
中的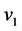 (
( )
) 中的
中的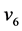 (
( ),再选择每个群中具有最小
),再选择每个群中具有最小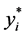 值的点,如
值的点,如 中的
中的 ,
,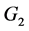 中的
中的 ,如果在每个群内至少有两个最大的
,如果在每个群内至少有两个最大的 值或者至少有两个最小的
值或者至少有两个最小的 值,则随机选择一个。
值,则随机选择一个。
如图2,令
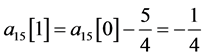 ,
,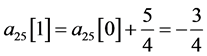 ,
,
 ,
,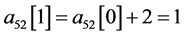 。
。
一些权值改变后,在下次迭代中,计算 ,
, ,并
,并
且执行与之前相同的步骤。重复上述步骤直到对任意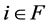 ,有
,有 。这个例子在三次迭代之后成立,最终边权如图3所示,可以看到图3为群平衡图。
。这个例子在三次迭代之后成立,最终边权如图3所示,可以看到图3为群平衡图。
B. 算法有效性分析
在每个群中,前提条件 意味着如果在迭代中的第三步有具有最大
意味着如果在迭代中的第三步有具有最大 值的点,则至
值的点,则至
少必有一个最小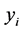 值的点,反之亦然。从迭代中第3)-ii)步中的权值改变,我们能发现
值的点,反之亦然。从迭代中第3)-ii)步中的权值改变,我们能发现
1) 与
与 的
的 值变为零;
值变为零;
2) 除了 ,
, ,
, 和
和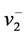 ,其他点的
,其他点的 值没有改变;
值没有改变;
3) 和
和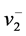 的
的 值增加了。
值增加了。

Figure 1. The weights of the edges in Example 1 and the initial values of  and
and 
图1. 例1中图的边权值及每个点的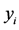 值,
值, 值的初始化
值的初始化

Figure 2. Some changes of weights in Example 1 after the procedure 4)-v)
图2. 例1中执行4)-v)后的边权改变

Figure 3. The weights of edges in Example 1 and the real-time values of  and
and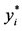 , when the graph reaches balance
, when the graph reaches balance
图3. 例1中达到平衡后的图的边权值及每个点的 值,
值,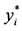 值
值
因此,有这样的事实:如果在某一步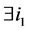 ,
, ,它将会永远都等于零。也就是说,在接下来的迭代中,它的值不会改变。基于以上的事实,如果一个点在某步迭代是平衡的,它将会永远平衡。并且在每次迭代中,每个群中至少一个点
,它将会永远都等于零。也就是说,在接下来的迭代中,它的值不会改变。基于以上的事实,如果一个点在某步迭代是平衡的,它将会永远平衡。并且在每次迭代中,每个群中至少一个点 值变为0,这个点是第3)-i)步中被选择的具有最大
值变为0,这个点是第3)-i)步中被选择的具有最大 值的点。在某次迭代中,某个群中也可能有两个点的
值的点。在某次迭代中,某个群中也可能有两个点的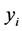 值变为0。如果最小
值变为0。如果最小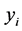 值也变为0,事实上,这一定出现在最后一步。因此,很容易发现,算法达到平衡所需的步数至多为
值也变为0,事实上,这一定出现在最后一步。因此,很容易发现,算法达到平衡所需的步数至多为 步。下面的定理给出了这一节的主要结论。
步。下面的定理给出了这一节的主要结论。
定理1:赋权有向图 达到群平衡条件(1)和(2)的迭代次数
达到群平衡条件(1)和(2)的迭代次数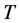 满足
满足 。
。
4. 赋权无向图的群平衡化算法
4.1. 含有两个子图且子图间连通的赋权无向图的群平衡化
定义1:对于包含两个子图的赋权无向图,如果去掉图中所有子图内的边后得到的图仍是连通的,就称此无向图的子图间是连通的;如果去掉图中子图内的所有边后得到的图是由 个连通分支构成的,就称此无向图的子图间是不连通的。
个连通分支构成的,就称此无向图的子图间是不连通的。
注:由于子图体现的是处于一个群内的个体间的拓扑关系,因此子图间关系连通表明:对于图中相同群内任意两点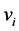 和
和 ,都能找到一个从
,都能找到一个从 到
到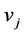 且满足以下条件的无圈路:存在一系列点
且满足以下条件的无圈路:存在一系列点  (奇数个),使得
(奇数个),使得 ,其中
,其中 ,
,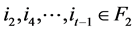 ,或者
,或者 ,
, 。
。
算法II
输入对象:一个有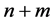 个点的赋权无向图
个点的赋权无向图 ,包含两个群,分别是有
,包含两个群,分别是有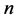 个点的赋权无向图
个点的赋权无向图 和有
和有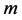 个点的赋权无向图
个点的赋权无向图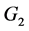 ,并且群间关系为连通的。
,并且群间关系为连通的。
初始化: ,如果
,如果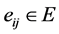 ,则
,则 ,否则
,否则 。
。
迭代:1)对于每个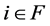 ,计算
,计算

如果对于任意的 ,有
,有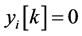 ,这表明群平衡条件达到,则退出算法。
,这表明群平衡条件达到,则退出算法。
2) 计算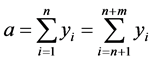 。如果
。如果 ,转3);如果
,转3);如果 ,转4)。
,转4)。
3) 由 知,对于每个群,群中所有点的群外邻接出权值之和为零,如果群内每个点的群外邻接出权值都为零,则群平衡条件达到,由此设计了(i)~(iii)。
知,对于每个群,群中所有点的群外邻接出权值之和为零,如果群内每个点的群外邻接出权值都为零,则群平衡条件达到,由此设计了(i)~(iii)。
(i) 在 中选择有最大
中选择有最大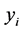 值的点
值的点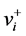 ,它的
,它的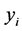 值表示为
值表示为 ,在
,在 中选择有最小
中选择有最小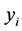 值的点
值的点 ,
,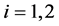 ;
;
(ii) 找到一个从 到
到 的无圈路
的无圈路 (由奇数个点组成)。
(由奇数个点组成)。
其中 ,
, ,
,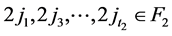 ,
, 。
。
令
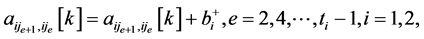
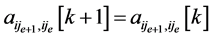 ,其中
,其中 。
。
(iii) 置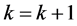 ,转1)并重复以上迭代。
,转1)并重复以上迭代。
4) 中所有点的邻接出权值之和与
中所有点的邻接出权值之和与 中所有点的邻接出权值之和都为
中所有点的邻接出权值之和都为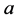 ,假设在
,假设在 中有
中有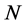 个点,
个点,
在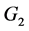 中有
中有 个点,如果
个点,如果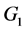 群内每个点的群外邻接出权值都为
群内每个点的群外邻接出权值都为 ,
, 群内每个点的群外邻接出权值都为
群内每个点的群外邻接出权值都为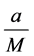 ,则对于每个群,群内每个点的群外邻接出权值相等,平衡条件达到。在(i)中定义
,则对于每个群,群内每个点的群外邻接出权值相等,平衡条件达到。在(i)中定义 作为
作为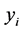 值与
值与
目的值的偏差,只要使每个点的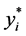 值都为零就达到了群平衡条件,以下为算法的具体步骤:
值都为零就达到了群平衡条件,以下为算法的具体步骤:
(i) 令 ,
,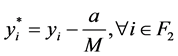 。如果对任意
。如果对任意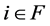 ,有
,有 ,则此时
,则此时 ,
, ,满足平衡条件(1)和(2),则群平衡达到,退出算法。
,满足平衡条件(1)和(2),则群平衡达到,退出算法。
以下(ii)-(iv)中与3)中的方法类似。
(ii) 在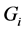 中选择有最大
中选择有最大 值的点
值的点 ,它的
,它的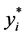 值表示为
值表示为 ,在
,在 中选择有最小
中选择有最小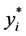 值的点
值的点 ,。
,。
(iii) 找到一个从 到
到 无圈路,
无圈路,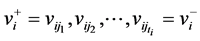 (由奇数个点组成),其中
(由奇数个点组成),其中

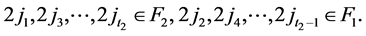
令


(iv) 置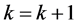 ,转1)并重复以上迭代。
,转1)并重复以上迭代。
下面,为了更直观地了解上述算法的各个步骤,我们给出一个算例。
例2:考虑赋权无向图图4,其中 ,点集
,点集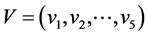 ,
, ,
,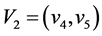 边集
边集 。假设
。假设 ,
,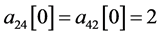 ,
, 。下面对其实施算法II。
。下面对其实施算法II。
计算 ,
,
 。
。
因为 中每个点至少有一个群外出邻居,因此计算
中每个点至少有一个群外出邻居,因此计算
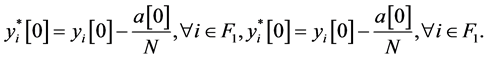
这部分算法演示如图4。
一旦计算出每个点的 值,转入计算(4)-(ii),并选择每个群中有最大
值,转入计算(4)-(ii),并选择每个群中有最大 值的点,如
值的点,如 中的
中的 ,
, 中的
中的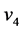 ,再选择每个群中具有最小
,再选择每个群中具有最小 值的点,如
值的点,如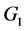 中的
中的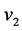 ,
, 中的
中的 ,如果在每个群内至少有两个最大的
,如果在每个群内至少有两个最大的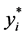 值或者至少有两个最小的
值或者至少有两个最小的 值,则随机选择一个。选择一条
值,则随机选择一个。选择一条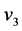 到
到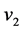 的路,例如:路
的路,例如:路 ,
,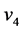 ,
, ,则
,则
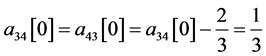 ,
, 。
。
选择另一条 到
到 的路,例如:路
的路,例如:路 ,
,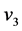 ,
,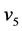 ,则
,则
 ,
,
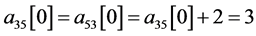 ,
,
即 ,
,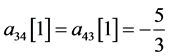 ,
,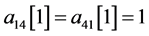 ,
, ,
, ,如图5。
,如图5。
一些权值改变后,在下次迭代中,重新计算
 ,
,
并且执行与之前相同的步骤。这个过程被重复直到对任意 ,有
,有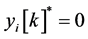 。这个例子发生在两次迭代之后,最终边权如图6所示,图6为被群平衡后的图。
。这个例子发生在两次迭代之后,最终边权如图6所示,图6为被群平衡后的图。
4.2. 含有两个子图且子图间有s (s > 1)个连通分支的赋权无向图的群平衡化
算法III
输入对象:一个有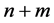 个点的赋权无向图
个点的赋权无向图 ,它包含两个子图,分别是有
,它包含两个子图,分别是有 个点的赋权无向图
个点的赋权无向图 和有
和有 个点的赋权无向图
个点的赋权无向图 。并且群间关系为有
。并且群间关系为有 个连通分支的赋权无向图。
个连通分支的赋权无向图。
初始化: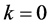 ,如果
,如果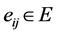 ,则
,则 ,否则
,否则 。
。
1) 如果对每个连通分支,有 ,其中
,其中 代表第
代表第 个连通分支中所有点的
个连通分支中所有点的 值总和。对于每个连通分支,算法类似于4.1-3),若每个连通分支达到群平衡,则此无向图达到群平衡。
值总和。对于每个连通分支,算法类似于4.1-3),若每个连通分支达到群平衡,则此无向图达到群平衡。
2) 如果 ,
,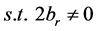 ,
,
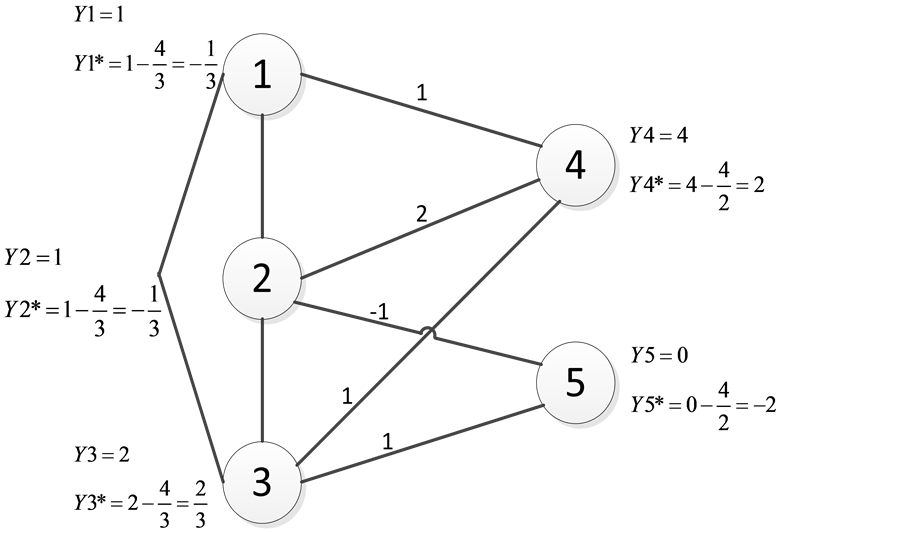
Figure 4. The weights of the edges in Example 2 and the initial values of  and
and 
图4. 例2中图的边权值及每个点的 值,
值, 值的初始化
值的初始化
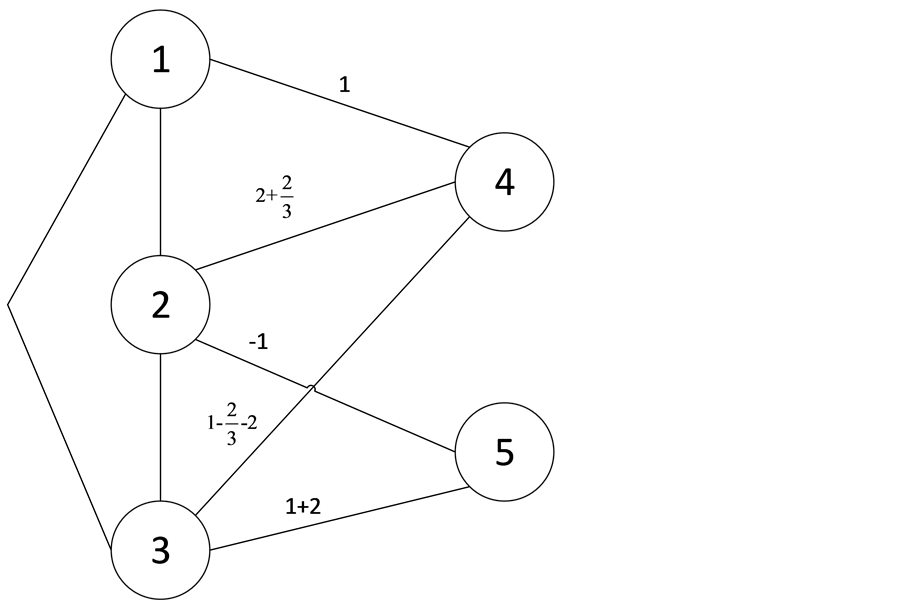
Figure 5. Some changes of weights in Example 2 after the procedure 4)-iii)
图5. 例2中执行4)-iii)后的边权改变

Figure 6. The weights of edges in Example 2 and the real-time values of  and
and , when the graph reaches balance
, when the graph reaches balance
图6. 例2中达到平衡后的图的边权值及每个点的 值,
值, 值
值
情况1:若 中存在没有群外出邻居的点,让第
中存在没有群外出邻居的点,让第 个连通分支中的某一边的边权值减
个连通分支中的某一边的边权值减 ,重新计算
,重新计算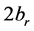 。若
。若 ,则转1)。
,则转1)。
情况2:若 中每个点至少有一个群外出邻居,则算法转3)。
中每个点至少有一个群外出邻居,则算法转3)。
3) 计算
 中所有点的邻接出权值之和为
中所有点的邻接出权值之和为 ,假设在
,假设在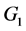 中有
中有 个点,若
个点,若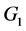 群内每个点的群外邻接出权值都为
群内每个点的群外邻接出权值都为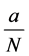 ,则
,则 群内每个点的群外邻接出权值相等,要使每个连通分支都达到群平衡,则
群内每个点的群外邻接出权值相等,要使每个连通分支都达到群平衡,则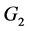 群内每个点的群外邻接出权值需都为
群内每个点的群外邻接出权值需都为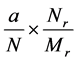 ,
,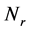 和
和 分别代表第
分别代表第 个连通分支中
个连通分支中 和
和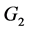 中点的个数。在4)中定义
中点的个数。在4)中定义 作为
作为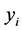 值与目的值的偏差,只要使每个点的
值与目的值的偏差,只要使每个点的 值都为零就达到了群平衡条件。以下为算法的具体步骤:
值都为零就达到了群平衡条件。以下为算法的具体步骤:
4) 令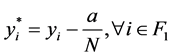 ,
, ,
,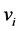 是既在
是既在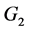 中也在第
中也在第 个连通分支中的点,其中
个连通分支中的点,其中 。
。
5) i) 如果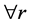 ,有
,有 (
( 是第
是第 个连通分支中的点),则对于每个连通分支,算法类似于4.1-4),目的是每个连通分支达到群平衡。
个连通分支中的点),则对于每个连通分支,算法类似于4.1-4),目的是每个连通分支达到群平衡。
ii) 如果 ,
,
 ,(
,( 是第
是第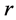 个连通分支中的点),让第
个连通分支中的点),让第 个连通分支中某一边的边权值减
个连通分支中某一边的边权值减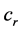 ,则重新计算
,则重新计算 (
( 是第
是第 个连通分支中的点),则
个连通分支中的点),则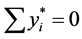 (
(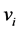 是第
是第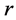 个连通分支中的点)。
个连通分支中的点)。
目标是使得任意的 ,
, ,对于每个连通分支,算法类似于4.1-4)。
,对于每个连通分支,算法类似于4.1-4)。
在每个连通分支平衡后有, ,
, ;对于既在第
;对于既在第 个连通分支中也在
个连通分支中也在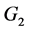 中的点,有
中的点,有 ,其中
,其中 ,
,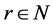 。易知,当
。易知,当 时,平衡条件(1)满足,但是只有
时,平衡条件(1)满足,但是只有 为常数时,条件(2)才能成立。如果
为常数时,条件(2)才能成立。如果 不为常数,则图不能通过算法III实现平衡。下面通过一个反例验证这个结论。
不为常数,则图不能通过算法III实现平衡。下面通过一个反例验证这个结论。
例3. 考虑图7中的无向图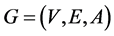 ,点集
,点集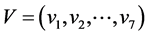 ,
, ,
, ,边集
,边集 ,
, 。假设
。假设 ,
, 。
。
由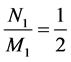 ,
, 有
有 。因此算法III不能平衡该图。下面验证此结论。
。因此算法III不能平衡该图。下面验证此结论。
计算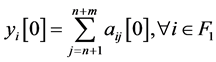 ,
,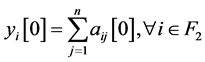 。
。 ,
, 。
。
因为 中每个点都有群外出邻居,计算
中每个点都有群外出邻居,计算 ,则
,则 ,
,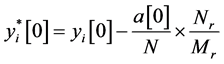 ,其中
,其中 是既在
是既在 中也在第
中也在第 个连通分支中的点。这部分算法演示如图7。由算法(5)-ii),因为
个连通分支中的点。这部分算法演示如图7。由算法(5)-ii),因为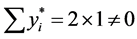 (
(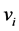 是第1个连通分支中的点),
是第1个连通分支中的点),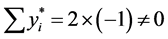 (
( 是第2个连通分支中的点)。
是第2个连通分支中的点)。
令 ,
, ,如图8。
,如图8。
重新计算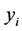 和
和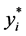 ,则
,则 ,
, (
( 是第
是第 个连通分支中的点)。
个连通分支中的点)。
对于每个连通分支,算法类似于4.1-4)。
这个例子两次迭代后有,对任意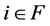 ,有
,有 。此时
。此时 ,
, ,
, ,不满足平衡条件(2)。至此,可以看到,该图不能被群平衡化,见图9。关于无向图的算法的有效性分析,由于其与有向图的算法分析类似,因此这里不再重复。基于以上的分析,很容易得到下面的定理:
,不满足平衡条件(2)。至此,可以看到,该图不能被群平衡化,见图9。关于无向图的算法的有效性分析,由于其与有向图的算法分析类似,因此这里不再重复。基于以上的分析,很容易得到下面的定理:
定理2. 对于如下两种图
i) 包含两个子图且子图间连通的赋权无向图;
ii) 满足 为常数的包含两个子图且子图间不连通的赋权无向图;
为常数的包含两个子图且子图间不连通的赋权无向图;
达到条件(1)和(2)的迭代次数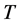 满足
满足 ,其中
,其中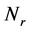 和
和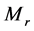 分别代表第
分别代表第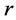 个连通分支中包含
个连通分支中包含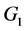 和
和 中点的个数。
中点的个数。
5. 结论
本文设计了两种关于群平衡化一般的赋权有向图和赋权无向图的分布式算法,我们通过理论和例子分别分析和演示了算法的有效性。值得指出的是这两种算法对初始图本身无任何限制,且都可以在有限步之后使得一个图达到群平衡。因此所设计的算法可以应用于一般的赋权有向图和赋权无向图,对解决群平均一致性提供了一定的理论基础。虽然本文提出了针对赋权有向图和赋权无向图的两种不同的群平衡化算法,但是本文所研究的结果只适用于含有两个子图的情形。在未来的工作中,我们将研究更有效的关于群平衡化的算法,并进一步讨论各个算法的优缺点。同时,对于含有三个以上的子图设计有效的分布式算法使其达到某种平衡也是未来值得研究的一个问题。
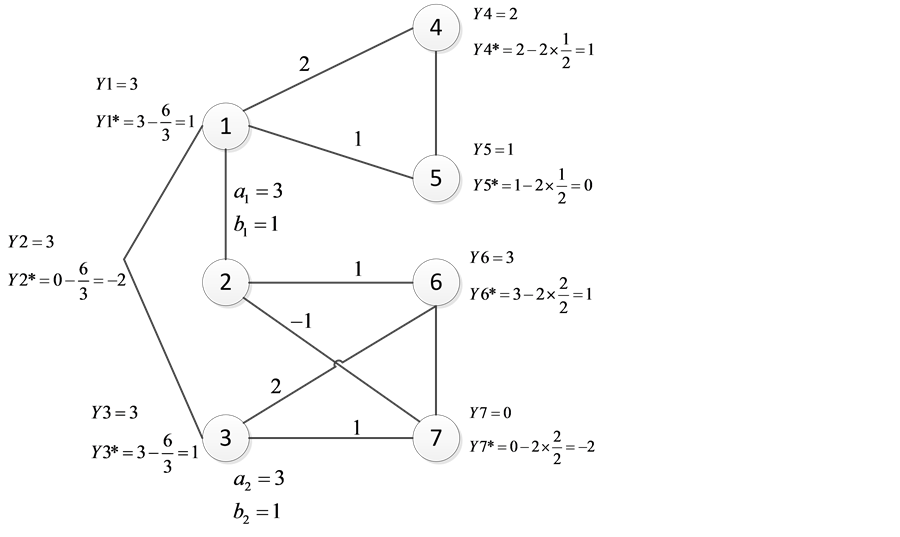
Figure 7. The weights of the edges in Example 3 and the initial values of  and
and 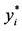
图7. 例3中图的边权值及每个点的 值,
值, 值的初始
值的初始

Figure 8. Some changes of weights in Example 3 after the procedure 5)-ii)
图8. 例3中执行5)-ii)的边权改变
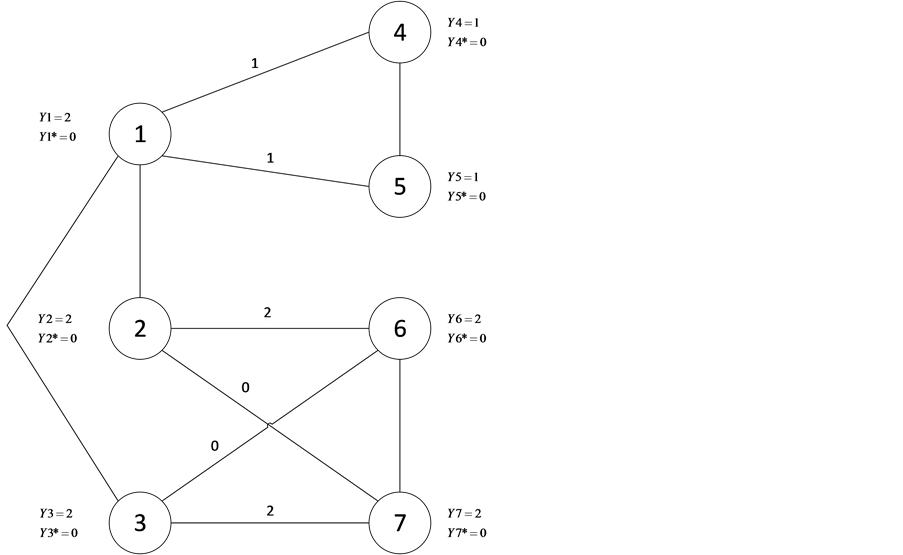
Figure 9. The graph in Example 3 cannot reach balance
图9. 例3中的图不能被平衡
基金项目
国家自然基金(61004031, 61104141, 61473061, 61403064),中央高校基本业务费(ZYGX2010J108, ZYGX2013Z005)。
文章引用
杨繁,于俊燕,高玉兰,禹梅,邵晋梁. 群平衡化赋权有向图/无向图的分布式算法研究
Distributed Strategies for Group-Balancing General Weighted Directed/Undirected Graphs[J]. 应用数学进展, 2016, 05(03): 472-486. http://dx.doi.org/10.12677/AAM.2016.53058
参考文献 (References)
- 1. Olfati-Saber, R. and Murray, R.M. (2003) Consensus Protocols for Networks of Dynamic Agents. Proceedings of the American Con-trol Conference, Denver, 4-6 June 2003, 951-956.
- 2. Olfati-Saber, R. and Murray, R.M. (2004) Consensus Problems in Networks of Agents with Switching Topology and Time Delay. IEEE Transactions on Automatic Control, 49, 1520-1533. http://dx.doi.org/10.1109/TAC.2004.834113
- 3. Ren, W. and Bward, R.W. (2005) Consensus Seeking in Multi-Agent Systems under Dynamically Charging Interaction Topologies. IEEE Transactions on Automatic Control, 50, 655-661. http://dx.doi.org/10.1109/TAC.2005.846556
- 4. Xiao, F. and Wang, L. (2006) State Consensus for Multi-Agent Systems with Switching Topologies and Time-Varying Delays. International Journal of Control, 79, 1277-1284. http://dx.doi.org/10.1080/00207170600825097
- 5. Xiao, F. and Wang, L. (2008) Consensus Protocols for Discrete-Time Mul-ti-Agent Systems with Time-Varying Delays. Automatica, 44, 2577-2582. http://dx.doi.org/10.1016/j.automatica.2008.02.017
- 6. Xiao, F. and Wang, L. (2008) Asynchronous Consensus in Conti-nuous-Time Multi-Agent Systems with Switching Topology and Time-Varying Delays. IEEE Transactions on Automatic Control, 53, 1804-1816. http://dx.doi.org/10.1109/TAC.2008.929381
- 7. Xiao, F. and Wang, L. (2006) Consensus Problems of Multi-Agent Systems under Discrete Communication Structure. Proceedings of the IEEE Conference on Decision and Control, San Diego, 13-15 December 2006, 4289-4294. http://dx.doi.org/10.1109/CDC.2006.376956
- 8. Xiao, F. and Wang, L. (2006) Consensus Behavior of Agents in Networked Systems under General Communication Topologies. Proceedings of the 2006 IEEE International Symposium on Intelligent Control, Munich, 4-6 October 2006, 862-867.
- 9. Ren, W. and Atkins, E. (2007) Distributed Multi-Vehicle Coordinated Control via Local Information Exchange. International Journal of Robust and Nonlinear Control, 17, 1002-1033. http://dx.doi.org/10.1002/rnc.1147
- 10. Xie, G.M. and Wang, L. (2007) Consensus Control for a Class of Networks of Dynamic Agents. International Journal of Robust and Nonlinear Control, 17, 941-959. http://dx.doi.org/10.1002/rnc.1144
- 11. Lin, P. and Jia, Y.M. (2009) Consensus of Second-Order Discrete-Time Multi-Agent Systems with Non-Uniform Time-Delays and Dynamically Changing Topologies. Automatica, 45, 2154-2158. http://dx.doi.org/10.1016/j.automatica.2009.05.002
- 12. Yu, W.W. and Chen, G. (2010) Second-Order Consensus for Mul-ti-Agent Systems with Directed Topologies and Nonlinear Dynamics. IEEE Transactions on Systems, Man, and Cybernetics Society, 40, 881-891.
- 13. Sun, Y.G. and Wang, L. (2009) Consensus of Multi-Agent Systems in Directed Networks with Non-Uniform Time- Varying Delays. IEEE Transactions on Automatic Control, 54, 1607-1613. http://dx.doi.org/10.1109/TAC.2009.2017963
- 14. Li, T. and Zhang, J.F. (2009) Mean Square Average-Consensus under Mea-surement Noises and Fixed Topologies. Automatica, 45, 1929-1936. http://dx.doi.org/10.1016/j.automatica.2009.04.017
- 15. Zheng, Y.S. and Wang, L. (2012) Finite-Time Consensus of Hetero-geneous Multi-Agent Systems with and without Velocity Measurements. Systems and Control Letters, 61, 871-878. http://dx.doi.org/10.1016/j.sysconle.2012.05.009
- 16. Zheng, Y.S. and Wang, L. (2012) Distributed Consensus of Heterogeneous Multi-Agent Systems with Fixed and Switching Topologies. International Journal of Control, 85, 1967-1976. http://dx.doi.org/10.1080/00207179.2012.713986
- 17. Zheng, Y.S. and Wang, L. (2016) Consensus of Switched Multi-Agent Systems. IEEE Transactions on Circuits and Systems, 63, 314-318.
- 18. Yu, J.Y. and Wang, L. (2009) Group Consensus of Mul-ti-Agent Systems with Undirected Communication Groups. Proceedings of the 7th Asian Control Conference, Hong Kong, 27-29 August 2009, 105-110.
- 19. Yu, J.Y. and Wang, L. (2010) Group Consensus in Multi Agent Systems with Switching Topologies and Communication Delays. Systems & Control Letters, 59, 340-348. http://dx.doi.org/10.1016/j.sysconle.2010.03.009
- 20. Yu, J.Y. and Wang, L. (2012) Group Consensus of Multi-Agent Systems with Directed Information Exchange. International Journal of Systems Science, 43, 334-348. http://dx.doi.org/10.1080/00207721.2010.496056
- 21. Chen, Y. and Lv, J.H. (2011) On the Cluster Consensus of Discrete-Time Multi-Agent Systems. Systems & Control Letters, 60, 517-523. http://dx.doi.org/10.1016/j.sysconle.2011.04.009
- 22. Qin, J.H. and Yu, C.B. (2013) Cluster Consensus Control of Generic Linear Multi-Agent Systems under Directed Topology with Acyclic Partition. Automatica, 49, 2898-2905. http://dx.doi.org/10.1016/j.automatica.2013.06.017
- 23. Han, Y.J. and Yu, W.W. (2013) Cluster Consensus in Discrete-Time Networks of Multi-Agents with Inter-Cluster Nonlinear Inputs. IEEE Transactions on Neural Networks and Learning Systems, 24, 566-578. http://dx.doi.org/10.1109/TNNLS.2013.2237786
- 24. Xie, D.M. and Liu, Q.L. (2014) Necessary and Sufficient Condition for Group Consensus of Multi-Agent Systems. Applied Mathematics and Computation, 243, 870-878. http://dx.doi.org/10.1016/j.amc.2014.06.069
- 25. Tan, C. and Liu, G.P. (2011) Group Consensus of Networked Multi-Agent Systems with Directed Topology. Proceedings of the 28th IFAC World Congress, Milano, 28 August-2 September 2011, 8878-8883. http://dx.doi.org/10.3182/20110828-6-it-1002.02690
- 26. Hadjicostis, C.N. and Rikos, A. (2012) Distributed Strategies for Balancing a Weighted Digraph. Proceedings of the 20th Mediterranean Conference on Control and Automation, Barcelona, 3-6 July 2012, 1141-1146. http://dx.doi.org/10.1109/med.2012.6265792
- 27. Apostolos, I.R. and Cristoforos, N.H. (2013) Distributed Balancing of a Di-graph with Integer Weights. Proceedings of the IEEE Conference on Decision Control, Firenze, 10-13 December 2013, 1983-1988.
- 28. Attilio, P. and Andera, R. (2013) A Decentralized Algorithm for Balancing a Strongly Connected Weighted Digraph. Proceedings of the American Control Conference, Washington DC, 17-19 June 2013, 6547-6552.
- 29. Fan, Y. and Han, R.Z. (2015) Graph-Balancing Algorithms for Average Consensus over Directed Networks. International Journal of Systems Science, 47, 135-148. http://dx.doi.org/10.1080/00207721.2015.1029720