ABSTRACT

In this paper, the dynamic behavior of a class of discrete population models is studied. Fixed point types and hyperbolic properties are determined by discussing coefficient parameters. By using central manifold theorem and bifurcation theory, we obtain the conditions of transcritical bifurcation and flip bifurcation at two fixed points.

Keywords:Discrete Population Model, Central Manifold Theorem, Transcritical Bifurcation, Flip Bifurcation

一类离散种群模型的动力学性质

陈雨青，张渝曼，徐江明，周效良

岭南师范学院数学与统计学院，广东 湛江

收稿日期：2019年7月31日；录用日期：2019年8月15日；发布日期：2019年8月22日

摘 要

本文研究了一类离散种群模型的动力学行为，通过讨论系数参数确定不动点类型及双曲性质。利用中心流形定理与分岔理论得到两个不动点产生跨临界分岔和flip分岔的条件。

关键词 :离散种群模型，中心流形定理，跨临界分岔，Flip分岔

Copyright © 2019 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

近几十年来，人们对种群动力学进行了广泛的研究，目前，已有许多文献研究环境参数对种群持续生存的影响 [1] [2] [3] [4] 。研究种群模型的稳定性和分岔性质，不仅可以得到系统解随时间变化的性态，还可以得到系统受外界干扰时系统解的性态变化，从而得到种群的演化规律，这对于预测种群在未来的发展状况并采取相应的措施具有广泛的理论意义。

在过去的几十年里，非线性差分方程在研究种群动力学方面发挥了重要作用，许多学者提出了包含各种复杂性种群模型 [2] [5] [6] [7] [8] [9] ，Newman等人在文献 [2] 中提出了一个非线性差分方程组，旨在描述两斑块种群之间的相互作用。本文研究 [2] 提出的一般模型并假设其活跃种群具有Beverton-Holt生长速率，用差分方程稳定性理论和分岔理论探讨这个模型的动力学行为。

设 $x\left(t\right)$ 和 $y\left(t\right)$ 分别表示在时间 $t=0,1,2,\cdots$ 时活跃种群和被动种群的密度。Newman等人在 [2] 中提出的活跃种群和被动种群之间的离散模型如下

$\{\begin{array}{l}x\left(t+1\right)=\left(1-\epsilon \right)f\left(x\left(t\right)\right)+\epsilon y\left(t\right),\\ y\left(t+1\right)=\left(1-\epsilon \right)y\left(t\right)+\epsilon f\left(x\left(t\right)\right),\\ x\left(0\right)\ge 0,y\left(0\right)\ge 0,x\left(0\right)+y\left(0\right)>0,\end{array}$

函数f描述了活跃种群的密度依赖性繁殖，在文献 [3] 中，为了排除Newman等人在 [2] 中探讨的混沌行为，假设增长函数f是单调的。f满足的条件如下：当 $x\in \left[0,\infty \right)$ 时， $f\left(0\right)=0,f^{\prime }\left(x\right)>0$ ；当 $x>0$ 时，存在正的常数C，当 $x\ge 0$ 时，有 $f\left(x\right)\le C$ 。本文我们令 $f=\frac{\gamma x}{1+kx}$ ，当 $f^{\prime }\left(0\right)=\gamma ,f^{″}\left(x\right)<0$ 时，对 $\forall x\ge 0$ 上述模型变为

$\{\begin{array}{l}x\left(t+1\right)=\frac{\left(1-\epsilon \right)\gamma x\left(t\right)}{1+kx\left(t\right)}+\epsilon y\left(t\right),\\ y\left(t+1\right)=\left(1-\epsilon \right)y\left(t\right)+\frac{\epsilon \gamma x\left(t\right)}{1+kx\left(t\right)},\end{array}$ (1)

其中 $\gamma$ 表示为密度无关增长率，k指种群容纳量， $\epsilon$ 表示斑块间的扩散率。系数参数满足： $0<\epsilon <1,\lambda >0,k>0$ ，将(1)改写为平面映射得

$$ (2)

映射(2)有两个不动点： $E_0\left(0,0\right),E_1\left(x^{*},x^{*}\right)$ ，其中 $x^{\ast }=\frac{\gamma -1}{k}$ 。

本文的安排如下：在下一节讨论不动点 $E_0$ 的双曲和非双曲情形以及双曲不动点的类型和稳定性；在第三节，应用中心流形定理研究非双曲不动点的跨临界分岔和Flip分岔；在第四节进行了总结。

2. 双曲和非双曲情形

在本节，我们把 $\epsilon ,\gamma$ 作为参数，在 $$ 的参数空间上讨论不动点 $E_0,E_1$ 的双曲和非双曲情形。

2.1. 不动点 $E_0\left(0,0\right)$ 的性质

为讨论不动点 $E_0\left(0,0\right)$ 的双曲性质，定义如下符号：

${\gamma }_1^{*}=\frac{1+{\epsilon }_1}{1-3{\epsilon }_1},{\epsilon }_1=1-\epsilon ,l_1=\left\{\left(\gamma ,{\epsilon }_1\right)|0<{\epsilon }_1<1,\gamma =1\right\},l_2=\left\{\left(\gamma ,{\epsilon }_1\right)|0<{\epsilon }_1<\frac{1}{3},\gamma ={\gamma }_1^{*}\right\},$

$B_2=\left\{\left(\gamma ,{\epsilon }_1\right)|1<\gamma <{\gamma }_1^{*},0<{\epsilon }_1<\frac{1}{3}\right\},B_3=\left\{\left(\gamma ,{\epsilon }_1\right)|\gamma >{\gamma }_1^{*},0<{\epsilon }_1<\frac{1}{3}\right\}.$

定理2.1.1 不动点 $E_0\left(0,0\right)$ 有以下性质：

1) 不动点 $E_0$ 是非双曲的，当且仅当 $\left(\gamma ,{\epsilon }_1\right)$ 位于直线 $l_{1,2}$ 上；

2) 如果 $\left(\gamma ,{\epsilon }_1\right)\in B_0$ ，该不动点是渐近稳定的；

3) 如果 $\left(\gamma ,{\epsilon }_1\right)\in B_{1,2}$ ，该不动点是一个鞍点；如果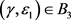，该不动点为不稳定的结点。

2.2. 不动点 $E_1\left(x^{\ast },x^{\ast }\right)$ 的性质

为讨论不动点 $E_1\left(x^{\ast },x^{\ast }\right)$ 的双曲性质，我们定义如下符号

${\gamma }_2^{*}=\frac{3\epsilon -2}{2-\epsilon },{\mathcal{D}}_1=\left\{\left(\gamma ,\epsilon \right)|0<\epsilon <1,\gamma =1\right\},{\mathcal{D}}_2=\left\{\left(\gamma ,\epsilon \right)|\frac{2}{3}<\epsilon <1,\gamma ={\gamma }_2^{*}\right\},$

${\mathcal{K}}_1=\left\{\left(\gamma ,\epsilon \right)|0<\epsilon \le \frac{2}{3},\gamma >1\right\},{\mathcal{K}}_2=\left\{\left(\gamma ,\epsilon \right)|\frac{2}{3}<\epsilon <1,\gamma >1\right\},$

${\mathcal{K}}_3=\left\{\left(\gamma ,\epsilon \right)|0<\epsilon <1,{\gamma }_2^{*}<\gamma <1\right\},{\mathcal{K}}_4=\left\{\left(\gamma ,\epsilon \right)|\frac{2}{3}<\epsilon <1,0<\gamma <{\gamma }_2^{*}\right\}.$

定理2.2.1 不动点 $E_1$ 有以下性质：

1) 不动点 $E_1$ 是非双曲的，当且仅当 $\left(\gamma ,\epsilon \right)\in {\mathcal{D}}_{1,2}$ ；

2) 如果 $\left(\gamma ,\epsilon \right)\in {\mathcal{K}}_{1,2}$ ，不动点 $E_1$ 是渐近稳定的；

3) 如果 $\left(\gamma ,\epsilon \right)\in {\mathcal{K}}_3$ ，不动点 $E_1$ 是鞍点；如果 $\left(\gamma ,\epsilon \right)\in {\mathcal{K}}_4$ ，不动点 $E_1$ 为不稳定结点。

3. 跨临界分岔和Flip分岔

本节考虑不动点 $$ 的跨临界分岔和flip分岔，选取 $\gamma$ 为分岔参数。

3.1. $E_0\left(0,0\right)$ 处的跨临界分岔和Flip分岔

从第2节可知，当 $\left(\gamma ,{\epsilon }_1\right)\in l_1$ 时，有，当 $$ ，有 ${\lambda }_2=-1,{\lambda }_1={\epsilon }_1+{\epsilon }_1\gamma +1$ ，定义如下符号：

$f_1={\epsilon }^2-{\epsilon }_1{\lambda }_2;f_2={\epsilon }^2-{\epsilon }_1{\lambda }_1;f_3={\epsilon }_1^2;f_4=\frac{{\epsilon }^2}{{\left(1+S\right)}^2}={\left(1-\epsilon \right)}^4.$

定理3.1.1 当 $\gamma =1$ 时，不动点 $E_0\left(0,0\right)$ 产生跨临界分岔。具体地讲，对 $\gamma$ 的微小扰动使得 $\gamma <1$ 时不动点 $E_0$ 是双曲且稳定的；当 $\gamma >1$ 时不动点 $E_0$ 双曲且不稳定。

证明：把 $\gamma$ 看作分岔参数并把F写成 $F_{\gamma }$ 来体现对 $$ 的依赖性，易得

$D{F}_{\gamma }\left(E_0\right)=\left[\begin{array}{cc}{\epsilon }_1\gamma & \left(1-{\epsilon }_1\right)\\ \left(1-{\epsilon }_1\right)\gamma & {\epsilon }_1\end{array}\right],$

其特征方程为 ${\lambda }^2-\left({\epsilon }_1+{\epsilon }_1\gamma \right)\lambda +2{\epsilon }_1\gamma -\gamma =0$ ，特征值为

${\lambda }_1=\frac{{\epsilon }_1\left(1+\gamma \right)-\sqrt{{\left({\epsilon }_1+\gamma {\epsilon }_1\right)}^2-8{\epsilon }_1\gamma +4\gamma }}{2},{\lambda }_2=\frac{{\epsilon }_1\left(1+\gamma \right)+\sqrt{{\left({\epsilon }_1+\gamma {\epsilon }_1\right)}^2-8{\epsilon }_1\gamma +4\gamma }}{2},$

特征值 ${\lambda }_1,{\lambda }_2$ 对应的特征向量为

${\left(\epsilon ,{\lambda }_1-{\epsilon }_1\gamma \right)}^{\tau },{\left(\epsilon ,{\lambda }_2-{\epsilon }_1\gamma \right)}^{\tau },$ (3)

利用特征向量组(3)得到如下变换

$\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{cc}-\epsilon & -\epsilon \\ {\lambda }_1-{\epsilon }_1\gamma & {\lambda }_2-{\epsilon }_1\gamma \end{array}\right]\left[\begin{array}{c}u\\ v\end{array}\right],$ (4)

由变换(4)可以把系统(1)变为

$\left[\begin{array}{c}u\\ v\\ \gamma \end{array}\right]\mapsto \left[\begin{array}{l}{\lambda }_{1}u\\ {\lambda }_{2}v\\ \gamma \end{array}\right]+\frac{1}{{\lambda }_2-{\lambda }_1}\left[\begin{array}{c}{f}_1\gamma \left(u+v\right)+f_3{\gamma }^2\left(u+v\right)-\frac{f_1\gamma \left(u+v\right)+f_3{\gamma }^2\left(u+v\right)}{1+k\epsilon \left(u+v\right)}\\ -f_2\gamma \left(u+v\right)-f_3{\gamma }^2\left(u+v\right)+\frac{f_2\gamma \left(u+v\right)+f_3{\gamma }^2\left(u+v\right)}{1+k\epsilon \left(u+v\right)}\\ 0\end{array}\right].$ (5)

当 $\left(\gamma ,{\epsilon }_1\right)\in l_1$ 时，有 ${\lambda }_2=1,{\lambda }_1={\epsilon }_1+{\epsilon }_1\gamma -1$ ，由文献 [10] 的定理2.1.4可知，令 ${\gamma }_1=\gamma -1$ ，在 $$ 附近，不动点 $\left(u,v\right)=\left(0,0\right)$ 的稳定性与分岔可通过研究在中心流形上一参数族映射来确定，中心流形有如下形式：

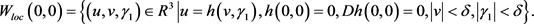
假设中心流形如下，

$u=h\left(v,{\gamma }_1\right)=a{v}^2+bv{\gamma }_1+c{\gamma }_1^2+\mathcal{O}\left(3\right).$

其中 $\mathcal{O}\left(3\right)$ 表示次数大于或等于3的项，由中心流形的不变性质可得，

$\begin{array}{l}\mathcal{N}\left(h\left(u,{\gamma }_1\right)\right)\\ =h\left(u,{\gamma }_1\right)-{\lambda }_{1}h\left(u,{\gamma }_1\right)-\frac{1}{{\lambda }_2-{\lambda }_1}\{f_1\left({\gamma }_1+1\right)\left[h\left(v,{\gamma }_1\right)+v\right]+f_3{\left({\gamma }_1+1\right)}^2\left[h\left(v,{\gamma }_1\right)+v\right]\begin{array}{c}\\ \end{array}\\ -\frac{f_1\left({\gamma }_1+1\right)\left[h\left(u,{\gamma }_1\right)+v\right]+f_3{\left({\gamma }_1+1\right)}^2\left[h\left(u,{\gamma }_1\right)+v\right]}{1+k\epsilon \left[h\left(v,{\gamma }_1\right)+v\right]}\}=0.\end{array}$

对比 $v^2,v{\gamma }_1,{\gamma }_1^2$ 的系数解得 $a=b=c=0$ ，因此系统(1)在 $\left(u,v\right)=\left(0,0\right)$ 附近中心流形为

$u=h\left(v,{\gamma }_1\right)=\mathcal{O}\left(3\right).$

将其代入(5)中的第二个等式可得一维映射

$v\mapsto {\Phi }_{{\gamma }_1}\left(v\right)={\lambda }_{2}v+\frac{1}{{\lambda }_2-{\lambda }_1}\left[-f_2\left({\gamma }_1+1\right)v-f_3{\left({\gamma }_1+1\right)}^{2}v+\frac{f_2\left({\gamma }_1+1\right)v+f_3{\left({\gamma }_1+1\right)}^{2}v}{1+kv}\right]+\mathcal{O}\left(3\right).$

当时，验算如下式子成立：

$\frac{\partial {\Phi }_{{\gamma }_1}}{\partial {\gamma }_1}\left(0,0\right)=0,\frac{\partial {\Phi }_{{\gamma }_1}}{\partial v\partial {\gamma }_1}\left(0,0\right)\ne 0,\frac{{\partial }^2\Phi }{\partial v^2}\left(0,0\right)\ne 0.$ (6)

根据文献 [10] 第369页公式知系统(1)在 $E_0$ 产生跨临界分岔，式子(6)表表明在 $$ 附近系统(1)的拓扑结构与如下式子的拓扑结构是局部拓扑等价的。

$v\mapsto {\Phi }_{{\gamma }_1}\left(v\right)={\lambda }_{2}v+\frac{1}{{\lambda }_2-{\lambda }_1}\left[-f_2\left({\gamma }_1+1\right)v-f_3{\left({\gamma }_1+1\right)}^{2}v+\frac{f_2\left({\gamma }_1+1\right)v+f_3{\left({\gamma }_1+1\right)}^{2}v}{1+kv}\right]$

定理3.1.2 当 $\left(\gamma ,{\epsilon }_1\right)\in l_2,{\alpha }_1\ne 0,{\alpha }_2\ne 0$ 时，系统(1)在不动点 $E_0\left(0,0\right)$ 经历Flip分岔。具体地讲，当 ${\alpha }_2>0$ 时，系统在不动点 $E_0\left(0,0\right)$ 处分岔出稳定的2周期轨；当 ${\alpha }_2<0$ 时，系统在不动点 $E_0\left(0,0\right)$ 分岔出的2周期轨是不稳定的。

证明：令 ${\gamma }_2=\gamma -{\gamma }_1^{*}$ ，计算得在 ${\gamma }_2$ 附近的中心流形为 $u=h\left(v,{\gamma }_2\right)=\mathcal{O}\left(3\right)$ 。

类似定理3.1.1的计算可得一维映射：

$\begin{array}{l}v\mapsto {\Phi }_{{\gamma }_2}\left(v\right)={\lambda }_{2}v+\frac{1}{{\lambda }_2-{\lambda }_1}[-f_2\left({\gamma }_2+{\gamma }_1^{*}\right)v-f_3{\left({\gamma }_2+{\gamma }_1^{*}\right)}^{2}v\begin{array}{c}\\ \underset{}{\overset{}{}}\end{array}\\ +\frac{f_2\left({\gamma }_2+{\gamma }_1^{*}\right)v+f_3{\left({\gamma }_2+{\gamma }_1^{*}\right)}^{2}v}{1+kv}]+\mathcal{O}\left(3\right).\end{array}$

当 $\left(\gamma ,{\epsilon }_1\right)\in l_2$ 时，有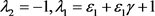，系统(1)在不动点 $E_0$ 有

${\left[\frac{\partial {\Phi }_{{\gamma }_2}}{\partial {\gamma }_2}\frac{{\partial }^2{\Phi }_{{\gamma }_2}}{\partial v^2}+2\frac{{\partial }^2{\Phi }_{{\gamma }_2}}{\partial v\partial {\gamma }_2}\right]|}_{\left(0,0\right)}={\alpha }_1\ne 0,{\left[\frac{1}{2}{\left(\frac{{\partial }^2{\Phi }_{{\gamma }_2}}{\partial v^2}\right)}^2+\frac{1}{3}\frac{{\partial }^3{\Phi }_{{\gamma }_2}}{\partial v^3}\right]|}_{\left(0,0\right)}={\alpha }_2\ne 0.$

其中

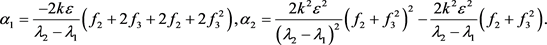
由文献 [11] 中的定理3.5.1可知，当 $\left(\gamma ,{\epsilon }_1\right)\in l_2,{\alpha }_1\ne 0,{\alpha }_2\ne 0$ 时不动点 $E_0$ 经历flip分岔。

3.2. $E_1\left(x^{\ast },x^{\ast }\right)$ 的跨临界分岔和Flip分岔

为讨论 $E_1\left(x^{\ast },x^{\ast }\right)$ 的分岔情况，我们定义如下符号：

$j_4=\epsilon {\epsilon }_1^2-\epsilon {\epsilon }_1{\lambda }_1\left({\gamma }_3+1\right)-{\epsilon }^3\left({\gamma }_3+1\right),j_5=\epsilon {\epsilon }_1^2-\epsilon {\epsilon }_1{\lambda }_2\left({\gamma }_4+{\gamma }_2^{*}\right)-{\epsilon }^3\left({\gamma }_4+{\gamma }_2^{*}\right),$

$j_6=\epsilon {\epsilon }_1^2-\epsilon {\epsilon }_1{\lambda }_1\left({\gamma }_4+{\gamma }_2^{*}\right)-{\epsilon }^3\left({\gamma }_4+{\gamma }_2^{*}\right),j_7={\epsilon }_1{\lambda }_2{\gamma }_2^{*}-{\epsilon }_1^2+{\epsilon }^2{\gamma }_2^{*}$

$j_8=1+e^{*}\frac{3\epsilon -2}{2-\epsilon },j_9=\epsilon {\epsilon }_1{\lambda }_2+{\epsilon }^3,e=\frac{2j_4}{\epsilon \left({\lambda }_1-{\lambda }_2\right)\left({\lambda }_2-1\right)},$

$e^{*}=\frac{2\left(3\epsilon -2\right)\left(2-\epsilon \right)j_6}{\epsilon {\lambda }_2\left({\lambda }_1-{\lambda }_2\right)\left({\lambda }_2-1\right){\left(3\epsilon -2\right)}^2-\epsilon j_6\left(8\epsilon -2\right)}.$

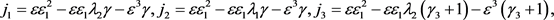
定理3.2.1 当 $$ 时，不动点 $E_1\left(x^{\ast },x^{\ast }\right)$ 发生跨临界分岔。具体地讲，对 $\gamma$ 的微小扰动使得 $\gamma <1$ 时不动点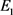是双曲且不稳定的；当 $$ 时不动点 $E_1$ 是非双曲的；当 $\gamma >1$ 时不动点 $$ 是双曲且稳定的，平衡点的稳定性在 $\gamma =1$ 处发生了交替。

证明：对于 $\left(\gamma ,\epsilon \right)\in {\mathcal{D}}_2$ ，我们有 ${\lambda }_1=1,{\lambda }_2=\frac{{\epsilon }_1+{\epsilon }_1\gamma }{\gamma }-1$ ，作平移变换 $\tilde{x}=x-x^{\ast }$ ，把不动点 $E_1\left(x^{\ast },x^{\ast }\right)$ 移动到 ${\tilde{E}}_1\left(0,0\right)$ 处，得到Jacobian矩阵，把 $\gamma$ 看作分岔参数且把 $\tilde{F}$ 写成 ${\tilde{F}}_{\gamma }$ 来体现对 $\gamma$ 的依赖性，易得

$D{\tilde{F}}_{\gamma }\left(E_1\right)=\left[\begin{array}{cc}\frac{{\epsilon }_1}{\gamma }& \epsilon \\ \frac{\epsilon }{\gamma }& {\epsilon }_1\end{array}\right],$

其特征方程为 $\gamma {\lambda }^2-\left({\epsilon }_1+{\epsilon }_1\gamma \right)\lambda +{\epsilon }_1^2-{\epsilon }^2=0$ ，易得特征值为

${\lambda }_1=\frac{\left({\epsilon }_1+{\epsilon }_1\gamma \right)\gamma -\sqrt{{\left({\epsilon }_1\gamma -{\epsilon }_1\right)}^2+4{\epsilon }^2\gamma }}{2\gamma },{\lambda }_2=\frac{\left({\epsilon }_1+{\epsilon }_1\gamma \right)\gamma +\sqrt{{\left({\epsilon }_1\gamma -{\epsilon }_1\right)}^2+4{\epsilon }^2\gamma }}{2\gamma },$

及特征值 ${\lambda }_1,{\lambda }_2$ 对应的特征向量为 ${\left(-\epsilon ,{\lambda }_1-\frac{{\epsilon }_1}{\gamma }\right)}^{\tau },{\left(-\epsilon ,{\lambda }_2-\frac{{\epsilon }_1}{\gamma }\right)}^{\tau }$ 。

利用变换 ${\left(x,y\right)}^{\tau }=T{\left(u,v\right)}^{\tau }$ ，则系统(1)变为

$\left[\begin{array}{c}u\\ v\\ \gamma \end{array}\right]\mapsto \left[\begin{array}{c}{\lambda }_{1}u\\ {\lambda }_{2}v\\ \gamma \end{array}\right]+\frac{1}{\epsilon \left({\lambda }_1-{\lambda }_2\right)}\left[\begin{array}{c}\frac{j_1\left(u+v\right)}{1-k\epsilon \left(u+v\right)}-\frac{j_1\left(u+v\right)}{{\gamma }^2}\\ -\frac{j_2\left(u+v\right)}{1-k\epsilon \left(u+v\right)}+\frac{j_2\left(u+v\right)}{{\gamma }^2}\\ 0\end{array}\right].$ (7)

其中

$T=\left[\begin{array}{cc}-\epsilon & -\epsilon \\ {\lambda }_1-\frac{{\epsilon }_1}{\gamma }& {\lambda }_2-\frac{{\epsilon }_1}{\gamma }\end{array}\right]$

$j_1=\epsilon {\epsilon }_1^2-\epsilon {\epsilon }_1{\lambda }_2\gamma -{\epsilon }^3\gamma ,j_2=\epsilon {\epsilon }_1^2-\epsilon {\epsilon }_1{\lambda }_1\gamma -{\epsilon }^3\gamma .$

令 ${\gamma }_3=\gamma -1$ ，假设在 ${\gamma }_3$ 附近的中心流形的形式为

$v=h\left(u,{\gamma }_3\right)=d{u}^2+eu{\gamma }_3+f{\gamma }_3^2+\mathcal{O}\left(3\right).$

中心流形满足

$\mathcal{N}\left(h\left(u,{\gamma }_3\right)\right)=h\left(u,{\gamma }_3\right)-{\lambda }_{2}h\left(u,{\gamma }_3\right)+\frac{1}{\epsilon \left({\lambda }_1-{\lambda }_2\right)}\{\frac{j_4\left(u+h\left(u,{\gamma }_3\right)\right)}{1-k\epsilon \left(u+h\left(u,{\gamma }_3\right)\right)}-\frac{j_4\left(u+h\left(u,{\gamma }_3\right)\right)}{{\left({\gamma }_3+1\right)}^2}\}=0.$

对比 $u^2,u{\gamma }_3,{\gamma }_3^2$ 的系数解得

$d=0,e=\frac{2j_4}{\epsilon \left({\lambda }_1-{\lambda }_2\right)\left({\lambda }_2-1\right)},f=0,$

故(8)表达式为

$v=h\left(u,{\gamma }_3\right)=eu{\gamma }_3+\mathcal{O}\left(3\right).$ (8)

将(8)代入(7)的第一个式子得映射

验算如下式子成立：

$\frac{\partial {\Phi }_{{\gamma }_3}}{\partial {\gamma }_3}\left(0,0\right)=0,\frac{\partial {\Phi }_{{\gamma }_3}}{\partial u\partial {\gamma }_3}\left(0,0\right)\ne 0,\frac{{\partial }^2{\Phi }_{{\gamma }_3}}{\partial u^2}\left(0,0\right)\ne 0.$

从而当 $\left(\gamma ,\epsilon \right)\in {\mathcal{D}}_2$ ，时，系统(1)在 $$ 产生跨临界分岔。

定理3.2.2 当 $\left(\gamma ,\epsilon \right)\in {\mathcal{D}}_2,{\alpha }_3\ne 0,{\alpha }_4\ne 0$ 时，系统(1)在不动点 $E_1\left(x^{\ast },x^{\ast }\right)$ 经历flip分岔；当 ${\alpha }_4>0$ 时，系统在不动点 $E_0$ 分岔出稳定的2周期轨；当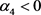时系统在不动点 $E_0$ 分岔出的2周期轨是不稳定的。

证明：当 $\left(\gamma ,\epsilon \right)\in {\mathcal{D}}_2$ 时，令 ${\gamma }_4=\gamma -{\gamma }_2^{*}$ ，在 $$ 附近的中心流形为 $v=h\left(u,{\gamma }_4\right)=e^{*}u{\gamma }_4+\mathcal{O}\left(3\right)$ ，其中

$e^{*}=\frac{2\left(3\epsilon -2\right)\left(2-\epsilon \right)j_6}{\epsilon {\lambda }_2\left({\lambda }_1-{\lambda }_2\right)\left({\lambda }_2-1\right){\left(3\epsilon -2\right)}^2-\epsilon j_6\left(8\epsilon -2\right)}.$

类似定理3.2.1计算可得到一维映射：

${\Phi }_{{\gamma }_4}\left(u\right)={\lambda }_{1}u+\frac{1}{\epsilon \left({\lambda }_1-{\lambda }_2\right)}\left[\frac{j_5\left(u+e^{*}u{\gamma }_4\right)}{1-k\epsilon \left(u+e^{*}u{\gamma }_4\right)}-\frac{j_5\left(u+e^{*}u{\gamma }_4\right)}{{\left({\gamma }_4+\frac{3\epsilon -2}{2-\epsilon }\right)}^2}\right]+\mathcal{O}\left(3\right).$

系统(1)在不动点 $E_1$ 发生flip分岔需满足：

${\left[\frac{\partial {\Phi }_{{\gamma }_4}}{\partial {\gamma }_4}\frac{{\partial }^2{\Phi }_{{\gamma }_4}}{\partial u^2}+2\frac{{\partial }^2{\Phi }_{{\gamma }_4}}{\partial u\partial {\gamma }_4}\right]|}_{\left(0,0\right)}={\alpha }_3\ne 0,{\left[\frac{1}{2}{\left(\frac{{\partial }^2{\Phi }_{{\gamma }_4}}{\partial u^2}\right)}^2+\frac{1}{3}\frac{{\partial }^3{\Phi }_{{\gamma }_4}}{\partial u^3}\right]|}_{\left(0,0\right)}={\alpha }_4\ne 0.$

其中

$\begin{array}{l}{\alpha }_3=-\frac{2}{\epsilon \left({\lambda }_1-{\lambda }_2\right)}\{2\epsilon j_2^2+k\epsilon j_8^2\left(j_9+\epsilon j_7{j}_8\right)+j_8\left(2k{e}^{*}{\epsilon }^2{j}_7+j_9\right)+\frac{j_9-2{\epsilon }^3}{{\left(3\epsilon -2\right)}^2}\\ -\frac{{\left(2-\epsilon \right)}^2\left(3e^{*}\epsilon -\epsilon -e^{*}+2\right)}{{\left(3\epsilon -2\right)}^2}+\frac{\left(2-\epsilon \right)\left[2\epsilon {\epsilon }_1^2+e^{*}\left(2-\epsilon \right)\right]+j_9}{{\left(3\epsilon -2\right)}^3}-\frac{\epsilon {\epsilon }_1^2\left(2-\epsilon \right)}{{\left(3\epsilon -2\right)}^4}\},\end{array}$

${\alpha }_4=\frac{2k^2{\epsilon }^2}{{\lambda }_1-{\lambda }_2}{j}_8^2\left[\frac{j_7^2}{{\lambda }_1-{\lambda }_2}-j_5{j}_8\right].$

从而当 $\left(\gamma ,\epsilon \right)\in {\mathcal{D}}_2,{\alpha }_3\ne 0,{\alpha }_4\ne 0$ 时，系统(1)在不动点 $E_1$ 经历flip分岔。

4. 总结

本文利用差分方程定性理论和分岔理论对一类离散种群模型进行了研究，由定理3.1.1和定理3.2.1可知，在不动点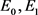处系统(1)的局部拓扑结构对参数 $\gamma$ 非常敏感，当 $\gamma$ 穿过1时， $E_0,E_1$ 的双曲性和稳定性都发生变化；当 $\gamma$ 穿过 ${\gamma }_2^{*}={\gamma }_2^{*}$ 时，系统不动点的个数和稳定性也发生变化，故参数 $\gamma$ 在1和 ${\gamma }_2^{*}$ 附近的微小变化与种群的演化规律之间有着某种对应的联系，人们可以通过研究离散种群模型的分岔性质来得到并且控制分岔参数，从而达到保护种群的目的。

基金项目

国家自然科学基金(No：11561019)；广东省攀登计划专项资金项目(No：pdjha0304/No：pdjh2019b0297);全国大学生创新创业训练计划项目(201910579725)。

文章引用

陈雨青,张渝曼,徐江明,周效良. 一类离散种群模型的动力学性质
Dynamic Properties of a Class of Discrete Population Model[J]. 应用数学进展, 2019, 08(08): 1463-1470. https://doi.org/10.12677/AAM.2019.88171

参考文献