Advances in Applied Mathematics
Vol.
08
No.
12
(
2019
), Article ID:
33529
,
12
pages
10.12677/AAM.2019.812236
Spatiotemporal Dynamics of a Planktonic Ecological Model with Inhibitory Effect
Quanli Ji
Zhejiang Provincial Key Laboratory for Water Environment and Marine Biological Resources Protection, Wenzhou University, Wenzhou Zhejiang
Received: Nov. 26th, 2019; accepted: Dec. 12th, 2019; published: Dec. 19th, 2019

ABSTRACT
Based on monitoring data of algae blooms and planktonic ecological theory, a planktonic ecological dynamical model with inhibitory effect has been established, and its qualitative theory and numerical simulations have been investigated. Theoretical studies mainly have considered the positivity and boundedness of model solutions, the existence and stability of equilibria, and the critical conditions for the Hopf bifurcation and Turing instability. Numerical simulations mainly have verified the effectiveness of the theoretical derivation and the feasibility of critical conditions. The obtained results can be very helpful to deepen and expand the research of nonlinear dynamics of such plankton ecosystem.
Keywords:Inhibitory Effect, Equilibrium, Stability, Hopf Bifurcation, Turing Instability

一类具有抑制效应的浮游生态模型的 时空动力学问题研究
姬圈利
温州大学浙江省水环境与海洋生物资源保护重点实验室,浙江 温州

收稿日期:2019年11月26日;录用日期:2019年12月12日;发布日期:2019年12月19日

摘 要
依据藻类水华监测数据与浮游生态学理论,构建一类具有抑制效应的浮游生态动力学模型,对其定性理论与数值工作进行研究。理论工作主要研究了模型解的正性与有界性、平衡点的存在性与稳定性,并给出模型发生霍普夫分支与图灵失稳的临界条件。数值工作主要验证了理论推导工作的有效性与临界条件的可行性。这些研究结果对浮游生态系统非线性动力学问题研究具有一定的促进作用。
关键词 :抑制效应,平衡点,稳定性,霍普夫分支,图灵失稳

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
浮游生物是指常常悬浮在水层中伴随水流移动的生物,一般可以分为浮游植物和浮游动物 [1] [2] [3],其特点是缺乏发达的运动器官,没有或仅有微弱的浮游能力,且大多数分布于水体的表层或者浅层。同时,浮游植物是浮游动物的主要食物来源,也是水域生物食物链的基本食物单元 [4],特别是它们可以通过光合作用吸收二氧化碳、释放氧气,在全球碳循环过程中发挥着极其重要的作用 [5]。
然而,随着经济社会的快速发展,由于工农业与生活所产生大量含氮磷的废水流入海洋、河流、湖泊等水域后,水体中的蓝藻、绿藻等浮游藻类大量繁殖致使水面呈现蓝色或绿色,这种现象出现在河流、湖泊等水体中常常被称为“有害藻类水华”。有害藻类大概被分为两类。第一类是毒死鱼类或污染海产品的产毒者,第二类是引起水生生物任意死亡的高密度分布的藻类 [6] [7]。近年来,“有害藻类水华”现象已变得越来越普遍 [8] [9] [10],例如,在1987年,有中国第三大淡水湖之称的太湖已经爆发大规模的藻类水华,从1987年到2007年,太湖藻类水华每年大概持续11.42天 [11] ;伊利湖是北美的第四大淡水湖,从2008年到2013年爆发大规模蓝藻水华,已给当地人民带去了巨大的经济损失,特别是2011年大概有240万美元的损失 [12]。显而易见,“有害藻类水华”已席卷亚洲、美洲等世界不同水域,所带来的经济损失越来越严重。
近年来,大量学者都在探究“有害藻类水华”爆发的相关机理,特别关注有害藻类水华扩散的实验调查和相关扩散动力学理论 [6] - [15]。文献 [6] 从现场调查数据与动力学模型两个方面揭示了产生毒素的浮游生物可以作为浮游植物水华的生物控制。文献 [14] 构建了一类具有添加食物效应的浮游植物与浮游动物时空动力学模型,研究发现有毒藻类和添加食物对藻类水华的发生具有显著影响,因而调控有毒藻类和添加食物的量可以控制藻类时空分布。文献 [15] 构建了一类带有抑制效应的湿地水域生态动力学时空模型,分析了非空间与空间系统局部和全局渐近稳定性,对系统霍普夫分支和图灵失稳等动力学性质进行研究,结果显示抑制效应不仅可以使均匀稳态失稳,而且还可以促使混沌现象发生。就目前而言,虽然大量学者都在研究藻类水华相关问题,但研究抑制效应和释放毒素如何协同影响藻类水华动态扩散的论文还是比较少的,因此,本论文构建了一类具有抑制效应浮游生态动力学新模型,对其定性理论与数值工作进行研究。
2. 建模
根据文献 [6] [14] [15],构建一类具有抑制效应的浮游生态动力学新模型,可以表示如下
 (1)
(1)
其中,p和z分别表示在时间t时刻浮游植物和浮游动物的生物量。从生物学的角度看,模型(1)中的参数均为正值,其生物学意义显示在表1中。
Table 1. Biological meaning of some parameters in the model (1)
表1. 模型(1)中部分参数的生物学含义
为了刻画空间区域中浮游生物之间的相互动态机制,模型(1)引入扩散项得模型(2)
 (2)
(2)
其中, 是带光滑边界
是带光滑边界 的有界空间区域,
的有界空间区域, 是一维空间的拉普拉斯算子,
是一维空间的拉普拉斯算子, 是单位外法向量,初始条件
是单位外法向量,初始条件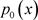 和
和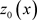 都是空间区域
都是空间区域 中的连续函数,
中的连续函数,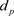 和
和 分别是浮游植物和浮游动物的自扩散系数。模型(2)采用零流边界条件,其表示在边界上没有外部输入,比较符合水域生态系统,如水库等。
分别是浮游植物和浮游动物的自扩散系数。模型(2)采用零流边界条件,其表示在边界上没有外部输入,比较符合水域生态系统,如水库等。
3. 非空间模型的定性分析
3.1. 解的正性和有界性
引理1:对于时间 时,模型(1)的所有从正初始值出发的解仍是正的。
时,模型(1)的所有从正初始值出发的解仍是正的。
证明:对于模型(1),容易得到下面的方程
 (3)
(3)
从上面的方程得到,当时间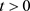 时,如果
时,如果 和
和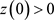 满足,那么
满足,那么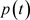 和
和 都是正的。引理得证。
都是正的。引理得证。
定理2:对于时间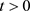 时,模型(1)的所有具有正初始值的解在
时,模型(1)的所有具有正初始值的解在 内是有界的。
内是有界的。
证明:假设 ,则
,则

进一步,得到下面的不等式
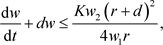
通过比较定理,得到

取极限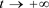 ,得到
,得到

因此,模型(1)所有具有正初始值的解在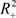 内是有界的。定理得证。
内是有界的。定理得证。
3.2. 平衡点的存在性与稳定性
考虑模型(1)平衡点的存在性与稳定性。首先,求模型(1)等倾线的交点,即有

模型(1)的平衡点有
i) 平凡平衡点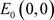 总是存在的;
总是存在的;
ii) 无浮游动物的平衡点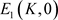 也总是存在的;
也总是存在的;
iii) 浮游生物共存平衡点(内平衡点) ,且
,且 和
和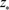 是下面方程的正根。
是下面方程的正根。
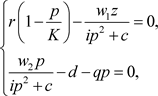
其中 ,
, ,
,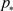 是下面函数
是下面函数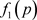 的正零点
的正零点
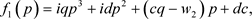
对函数 关于p进行简单的微分计算,给出下面的情形
关于p进行简单的微分计算,给出下面的情形
a) 如果 ,那么
,那么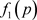 没有正零点,也就是说,共存平衡点
没有正零点,也就是说,共存平衡点 不存在。
不存在。
b) 如果 ,那么
,那么
当 时,
时, 没有正零点,也就是说,共存平衡点
没有正零点,也就是说,共存平衡点 不存在;
不存在;
当 时,
时, 有一个正零点,那么,存在一个平衡点
有一个正零点,那么,存在一个平衡点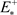 ;
;
当 时,
时, 有两个正零点,那么,存在两个平衡点
有两个正零点,那么,存在两个平衡点 和
和 。
。
其中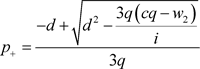 。
。
平衡点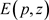 处雅可比矩阵为
处雅可比矩阵为
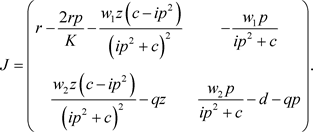
j) 在平衡点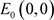 处雅可比矩阵为
处雅可比矩阵为

由于矩阵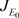 的特征值是r和
的特征值是r和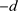 ,所以平衡点
,所以平衡点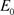 是一个鞍点。
是一个鞍点。
jj) 在平衡点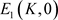 处雅可比矩阵为
处雅可比矩阵为
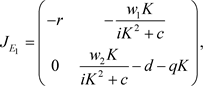
由于矩阵 的特征值是
的特征值是 和
和 ,当
,当 时,平衡点
时,平衡点 是局部渐近稳定的。
是局部渐近稳定的。
jjj) 在平衡点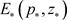 处雅可比矩阵为
处雅可比矩阵为
 (4)
(4)
如果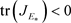 和
和 ,那么矩阵
,那么矩阵 的特征值有负实部。通过计算,容易得到
的特征值有负实部。通过计算,容易得到
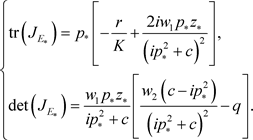
因此,当 和
和 成立时,平衡点
成立时,平衡点 是局部渐近稳定的。根据以上分析,可以得到下面的定理。
是局部渐近稳定的。根据以上分析,可以得到下面的定理。
定理3:模型(1)中平衡点的局部渐近稳定性分析
i) 平衡点 总是不稳定,并且是一个鞍点;
总是不稳定,并且是一个鞍点;
ii) 当 时,平衡点
时,平衡点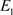 是局部渐近稳定的;
是局部渐近稳定的;
iii) 当 和
和 成立时,平衡点
成立时,平衡点 是局部渐近稳定的。
是局部渐近稳定的。
3.3. 内平衡点附近霍普夫分支分析
对于模型(1),在内平衡点附近进行扰动,有霍普夫分支发生,引起周期解的出现。接下来,考虑环境容纳量K作为分支参数,表明在临界值 时,霍普夫分支发生。
时,霍普夫分支发生。
定理4:对于模型(1)的内平衡点附近,霍普夫分支在参数值 处发生,其中,
处发生,其中,

证明:根据3.2部分的分析,模型(1)的内平衡点 附近雅可比矩阵
附近雅可比矩阵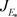 的特征方程为
的特征方程为
 (5)
(5)
特征方程的根是

当 时,如果
时,如果 满足,内平衡点
满足,内平衡点 是渐近稳定的;如果
是渐近稳定的;如果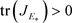 满足,内平衡点
满足,内平衡点 是不稳定的。解方程
是不稳定的。解方程 ,我们得到临界的分支点
,我们得到临界的分支点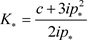 。应用霍普夫分支定理,验证横截性条件
。应用霍普夫分支定理,验证横截性条件 ,说明在内平衡点
,说明在内平衡点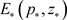 附近存在周期解,模型(1)发生霍普夫分支。
附近存在周期解,模型(1)发生霍普夫分支。
4. 时空模型
考虑时空模型(2)稳态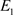 和
和 的稳定性分析。首先,对于模型(2)稳态
的稳定性分析。首先,对于模型(2)稳态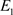 ,通过计算,得到下面的定理。
,通过计算,得到下面的定理。
定理5:对于时空模型(2)的稳态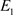 ,
,
i) 如果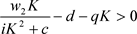 成立,那么稳态
成立,那么稳态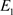 不稳定;
不稳定;
ii) 如果 成立,那么稳态
成立,那么稳态 稳定。
稳定。
证明:为了研究稳态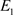 的稳定性,考虑稳态
的稳定性,考虑稳态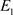 附近线性化算子相应的特征值问题。首先,时空模型(2)的稳态
附近线性化算子相应的特征值问题。首先,时空模型(2)的稳态 附近线性化系统为
附近线性化系统为
 (6)
(6)
其中,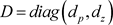 ,并且
,并且 在3.2部分中有显示。根据以上分析,时空模型(2)的稳态
在3.2部分中有显示。根据以上分析,时空模型(2)的稳态 附近线性化结果为
附近线性化结果为

 (7)
(7)

进而,时空模型(2)相应的特征方程为
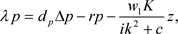
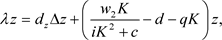 (8)
(8)

其中, 是(8)的特征值,
是(8)的特征值, 为相应的特征向量。
为相应的特征向量。
如果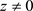 ,那么
,那么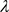 是带有零流边界条件算子
是带有零流边界条件算子 的特征值,进而特征值
的特征值,进而特征值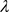 是实数。同理,如果
是实数。同理,如果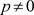 ,那么
,那么 也是实数。因此,(8)相应的特征方程的特征值都是实数。不妨设
也是实数。因此,(8)相应的特征方程的特征值都是实数。不妨设 是(8)中的最大特征值,考虑下面方程的比较特征值
是(8)中的最大特征值,考虑下面方程的比较特征值
 (9)
(9)
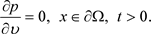
一方面,根据方程(9),如果 成立,那么比较特征值
成立,那么比较特征值 和相应的特征向量 均为正。另一方面,如果比较特征值
和相应的特征向量 均为正。另一方面,如果比较特征值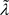 和相应的特征向量
和相应的特征向量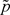 均为正且满足下面的方程(10),那么比较特征值
均为正且满足下面的方程(10),那么比较特征值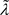 和相应的特征向量
和相应的特征向量 也满足方程(8)。
也满足方程(8)。
 (10)
(10)

因此,如果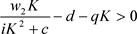 成立,那么
成立,那么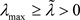 ,从而时空模型(2)的稳态
,从而时空模型(2)的稳态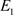 不稳定。(i)得证。
不稳定。(i)得证。
下面考虑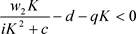 ,并且假设
,并且假设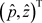 为(8)的最大特征值
为(8)的最大特征值 的相应特征向量。如果
的相应特征向量。如果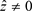 ,那么
,那么 也是(9)的一个特征值。同时,当
也是(9)的一个特征值。同时,当 时,那么
时,那么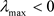 满足;如果
满足;如果 ,那么
,那么 ,并且
,并且 为下面方程(11)的一个特征值。明显地,(11)的最大特征值为
为下面方程(11)的一个特征值。明显地,(11)的最大特征值为 ,那么
,那么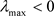 满足。
满足。
 (11)
(11)
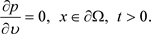
因此,如果 成立,那么
成立,那么 ,从而时空模型(2)的稳态
,从而时空模型(2)的稳态 是稳定的。(ii)得证。
是稳定的。(ii)得证。
对于模型(2)的稳态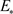 ,通过计算得到以下的定理。为了证明下面定理,引入引理6 [16]。
,通过计算得到以下的定理。为了证明下面定理,引入引理6 [16]。
引理6:考虑下面的方程:

 (12)
(12)

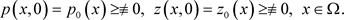
假设 为(12)的常数稳态,也就是说
为(12)的常数稳态,也就是说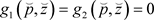 ,下面说明
,下面说明 什么情况一致渐近稳定。如果
什么情况一致渐近稳定。如果 ,
, ,
, ,
,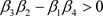 ,其中,
,其中,


那么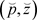 是一致渐近稳定的;如果
是一致渐近稳定的;如果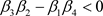 ,那么
,那么 是不稳定的。
是不稳定的。
定理7:对于时空模型(2)的稳态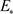 ,
,
i) 如果 和
和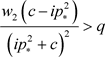 成立,那么稳态
成立,那么稳态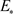 是一致渐近稳定的;
是一致渐近稳定的;
ii) 如果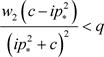 成立,那么稳态
成立,那么稳态 是不稳定的。
是不稳定的。
证明:考虑下面的式子




通过计算得到,如果 和
和 成立,那么
成立,那么 ,
,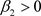 ,
,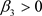 ,
,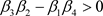 满足,应用引理6,i)得证;如果
满足,应用引理6,i)得证;如果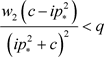 成立,那么
成立,那么 满足,应用引理6,ii)得证。
满足,应用引理6,ii)得证。
在时空模型中,图灵失稳经常会遇到。在图灵失稳临界值附近,系统空间对称性会被打破,这将导致时间上一致空间震荡的出现。对于时空模型(2)的稳态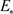 ,下面给出图灵失稳不会发生的定理。
,下面给出图灵失稳不会发生的定理。
定理8:对于时空模型(2)稳态 附近,不会发生图灵失稳。
附近,不会发生图灵失稳。
证明:考虑时空模型(2)在稳态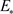 附近充分小的时空依赖扰动
附近充分小的时空依赖扰动
 (13)
(13)
其中, 是时间t上扰动的增长率,i是虚数单位并且
是时间t上扰动的增长率,i是虚数单位并且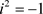 ,
, 和
和 充分小,
充分小,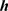 是二维空间的空间向量,
是二维空间的空间向量,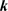 是平面中的波向量。把(13)代入模型(2)中,得到相应的特征矩阵
是平面中的波向量。把(13)代入模型(2)中,得到相应的特征矩阵
 (14)
(14)
相应的特征方程为
 (15)
(15)
其中, ,
,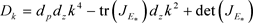 。
。
众所周知,图灵失稳意味着,由于种群的扩散效应,非空间模型中的稳定平衡点 在时空模型中变得不稳定。在非时空模型(1)中,平衡点
在时空模型中变得不稳定。在非时空模型(1)中,平衡点 的稳定条件为
的稳定条件为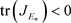 ,
, 。在时空模型(2)中,容易看出
。在时空模型(2)中,容易看出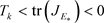 。因此,对于时空模型(2),在
。因此,对于时空模型(2),在 上,只有当
上,只有当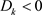 时,图灵失稳才会发生。但是,通过计算知道,在
时,图灵失稳才会发生。但是,通过计算知道,在 上,
上, 恒成立。所以,当条件
恒成立。所以,当条件 ,
,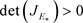 满足时,在时空模型(2)中,稳态
满足时,在时空模型(2)中,稳态 是局部渐近稳定的,也就是说,图灵失稳不会发生。定理得证。
是局部渐近稳定的,也就是说,图灵失稳不会发生。定理得证。
5. 数值模拟
众所周知,数值模拟可以验证理论结果的有效性与可行性。根据已有的文献 [12] [14] [15],考虑以下参数集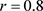 ,
, ,
, ,
, ,
, ,
,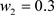 ,
, ,
, 。对于非空间模型(1),根据定理3,理论计算可以得到内平衡点
。对于非空间模型(1),根据定理3,理论计算可以得到内平衡点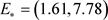 是局部渐近稳定的。取初始值
是局部渐近稳定的。取初始值 ,通过数值模拟,从时序图1(a)和相位图1(b)可以看出系统(1)的内平衡点
,通过数值模拟,从时序图1(a)和相位图1(b)可以看出系统(1)的内平衡点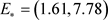 确实是局部渐近稳定的。
确实是局部渐近稳定的。

Figure 1. When ,
,  ,
,  ,
,  ,
,  ,
, 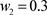 ,
,  ,
,  , the initial value is
, the initial value is , the equilibrium
, the equilibrium  of the system (1) is locally asymptotically stable. (a) Time evolution of Zooplankton and TPP; (b) Phase portrait of the system (1)
of the system (1) is locally asymptotically stable. (a) Time evolution of Zooplankton and TPP; (b) Phase portrait of the system (1)
图1. 当 ,
,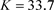 ,
, ,
, ,
,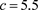 ,
, ,
, ,
, ,初始值取
,初始值取 ,系统(1)的平衡点
,系统(1)的平衡点 是局部渐近稳定的。(a)浮游动物与浮游植物的时序图;(b)系统(1)相位图
是局部渐近稳定的。(a)浮游动物与浮游植物的时序图;(b)系统(1)相位图
对于时空模型(2),根据定理8,常数稳态 附近没有图灵失稳发生。取以上的参数值,取初始值条件
附近没有图灵失稳发生。取以上的参数值,取初始值条件 ,
, ,且取
,且取 ,
,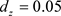 ,通过数值模拟,从图2和图3可以看出系统(2)的常数稳态
,通过数值模拟,从图2和图3可以看出系统(2)的常数稳态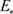 附近确实不会发生图灵失稳,只存在空间均匀周期解。其中,图3是图2相应的平面图。
附近确实不会发生图灵失稳,只存在空间均匀周期解。其中,图3是图2相应的平面图。

Figure 2. In the system (2), when ,
, 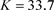 ,
, 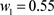 ,
, 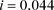 ,
,  ,
, 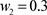 ,
, 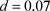 ,
,  ,
, 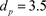 ,
,  , the initial conditions are
, the initial conditions are ,
, 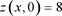 , there exist spatially homogeneous periodic solutions
, there exist spatially homogeneous periodic solutions
图2. 在系统(2)中,当 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,初始条件为
,初始条件为 ,
, ,存在空间均匀周期解
,存在空间均匀周期解
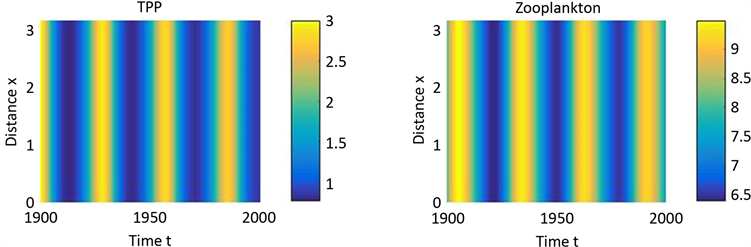
Figure 3. In the system (2), when ,
,  ,
,  ,
,  ,
, 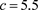 ,
,  ,
,  ,
,  ,
, 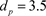 ,
,  , the initial conditions are
, the initial conditions are ,
,  , there exist spatially homogeneous periodic solutions
, there exist spatially homogeneous periodic solutions
图3. 在系统(2)中,当 ,
, ,
, ,
,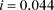 ,
, ,
,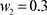 ,
, ,
, ,
, ,
, ,初始条件为
,初始条件为 ,
, ,存在空间均匀周期解
,存在空间均匀周期解
6. 结论
本文首先构建了一类具有抑制效应的浮游生态动力学新模型,讨论了非空间系统解的正性、有界性,平衡点的稳定性和霍普夫分支存在性,分析了空间模型边界稳态和正稳态的稳定性,以及正常数稳态附近图灵失稳情况。其次,数值模拟验证了理论结果的有效性与可行性,并模拟出空间模型所存在的空间均匀周期解。最后,期望这些研究结果有利于促进探究浮游生态模型的非线性动力学问题。
文章引用
姬圈利. 一类具有抑制效应的浮游生态模型的时空动力学问题研究
Spatiotemporal Dynamics of a Planktonic Ecological Model with Inhibitory Effect[J]. 应用数学进展, 2019, 08(12): 2050-2061. https://doi.org/10.12677/AAM.2019.812236
参考文献
- 1. Nørgaard, E. (1959) Fundamentals of Ecology. Oikos, 10, 290-291.
https://doi.org/10.2307/3565152 - 2. James, E.C. (1999) The Relative Importance of Light and Nutrient Limitation of Phytoplankton Growth: A Simple Index of Coastal Ecosystem Sensitivity to Nutrient. Aquatic Ecology, 33, 3-16.
https://doi.org/10.1023/A:1009952125558 - 3. El Abdllaoui, A., Chattopadhyay, J. and Arino, O. (2002) Comparisons by Models of Some Basic Mechanisms Acting on the Dynamics of the Zooplankton-Toxic Phytoplankton System. Mathematical Models and Methods in Applied Sciences, 12, 1421-1451.
https://doi.org/10.1142/S0218202502002185 - 4. Smetacek, V. and Klaas, C. (2012) Deep Carbon Export from a Southern Ocean Iron-Fertilized Diatom Bloom. Nature, 487, 313-319.
https://doi.org/10.1038/nature11229 - 5. Dai, C., Zhao, M. and Yu, H. (2016) Dynamics Induced by Delay in a Nutrient-Phytoplankton Model with Diffusion. Ecological Complexity, 26, 29-36.
https://doi.org/10.1016/j.ecocom.2016.03.001 - 6. Chattopadhayay, J., Sarkar, R. and Mandal, S. (2002) Toxin-Producing Plankton May Act as a Biological Control for Planktonic Blooms: Field Study and Mathematical Modelling. Journal of Theoretical Biology, 215, 333-344.
https://doi.org/10.1006/jtbi.2001.2510 - 7. Sarkar, R., Pal, S. and Chattopadhyay, J. (2005) Role of Two Toxin-Producing Plankton and Their Effect on Phytoplankton-Zooplankton System: A Mathematical Study Supported by Experimental Findings. Biosystems, 80, 11-23.
https://doi.org/10.1016/j.biosystems.2004.09.029 - 8. Goldyn, R. and Kowalczewska-Madura, K. (2008) Interactions between Phytoplankton and Zooplankton in the Hypertrophic Swarzedzkie Lake in Western Poland. Journal of Plankton Research, 30, 33-42.
https://doi.org/10.1093/plankt/fbm086 - 9. Wang, B., Zhao, M., Dai, C., Yu, H., Wang, N. and Wang, P. (2016) Dynamics Analysis of a Nutrient-Plankton Model with a Time Delay. Discrete Dynamics in Nature and Society, 2016, Article ID: 9797624.
https://doi.org/10.1155/2016/9797624 - 10. Wang, P., Zhao, M., Yu, H., Dai, C., Wang, N. and Wang, B. (2016) Nonlinear Dynamics of a Marine Phytoplankton-Zooplankton System. Advances in Difference Equations, 2016, Article ID: 212.
https://doi.org/10.1186/s13662-016-0935-y - 11. Duan, H., Ma, R., Xu, X., Kong, F., Zhang, S., Kong, W., Hao, J. and Shang, L. (2009) Two-Decade Reconstruction of Algal Blooms in China-Lake Taihu. Environmental Science & Technology, 43, 3522-3528.
https://doi.org/10.1021/es8031852 - 12. Li, J., Song, Y., Wan, L. and Zhu, H. (2017) Dynamical Analysis of a Toxin-Producing Phytoplankton-Zooplankton Model with Refuge. Mathematical Biosciences and Engineering, 14, 529-557.
https://doi.org/10.3934/mbe.2017032 - 13. Wang, W., Liu, S. and Liu, Z. (2019) Spatiotemporal Dynamics near the Turing-Hopf Bifurcation in a Toxic-Phytoplan- kton-Zooplankton Model with Cross-Diffusion. Nonlinear Dynamics, 98, 27-37.
https://doi.org/10.1007/s11071-019-05168-2 - 14. Wang, W., Liu, S., Tian, D. and Wang, D. (2018) Pattern Dynamics in a Toxin-Producing Phytoplankton-Zooplankton Model with Additional Food. Nonlinear Dynamics, 94, 211-228.
https://doi.org/10.1007/s11071-018-4354-3 - 15. Raw, S. and Mishra, P. (2019) Modeling and Analysis of Inhibitory Effect in Plankton-Fish Model: Application to the Hypertrophic Swarzedzkie Lake in Western Poland. Nonlinear Analysis. Real World Applications, 46, 465-492.
https://doi.org/10.1016/j.nonrwa.2018.09.026 - 16. Tian, Y. and Weng, P. (2011) Stability Analysis of Diffusive Predator-Prey Model with Modified Leslie-Gower and Holling-Type III Schemes. Applied Mathematics and Computation, 218, 3733-3745.
https://doi.org/10.1016/j.amc.2011.09.018
