一类高次非线性方程的孤立波分支 Bifurcations of Solitary Waves for a Class of Higher Order Nonlinear Equations

doi:10.12677/AAM.2020.98149

Advances in Applied Mathematics
Vol. 09 No. 08 ( 2020 ), Article ID: 37172 , 13 pages
10.12677/AAM.2020.98149

Bifurcations of Solitary Waves for a Class of Higher Order Nonlinear Equations

Lingling Zou, Rui Liu

●How to Cite this Article

School of Mathematics, South China University of Technology, Guangzhou Guangdong

Received: Jul. 26^th, 2020; accepted: Aug. 13^th, 2020; published: Aug. 20^th, 2020

ABSTRACT

In this article, we consider the solitary wave bifurcation of a class of higher order nonlinear equations with parameter k, whose traveling wave system has a singular line. In this article, the qualitative analysis theory and the bifurcation method of dynamical system are used to study the case of equation with degree three and four, the bifurcation wave velocity, bifurcation curve and the existence and bifurcation of solitary wave are obtained.

Keywords:Higher Order Equation, Qualitative Theory, Bifurcation Method, Solitary Wave, Bifurcation Wave Velocity

一类高次非线性方程的孤立波分支

邹玲玲，刘锐

华南理工大学数学学院，广东广州

收稿日期：2020年7月26日；录用日期：2020年8月13日；发布日期：2020年8月20日

摘要

本论文考虑一类含参数的高次非线性方程的孤立波分支，它们的行波系统都有一条奇直线。文章主要利用定性分析理论和动力系统分支方法，对方程次数为3和4的情形做出了研究，得出了各自情形下的分支波速、分支曲线以及孤立波的存在性和分支情况。

关键词 :高次方程，定性理论，分支方法，孤立波，分支波速

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

国内外许多学者研究过以下方程：

$u_{t} + 2 k u_{x} - u_{x x t} + (b + 1) u^{n} u_{x} - b u_{x} u_{x x} - u u_{x x x} = 0$ ， (1-1)

当 $k = 0$ ， $b > 1$ ，n为任意正整数时，Yang [1] 等人考虑了方程(1-1)的尖波和反尖波的存在性和分支。当 $k = 0$ ， $b = 1$ ， $n = 2$ 时，Li和Liu [2] 研究发现方程(1-1)具有的全局性质的周期波和孤立波，并计算出波解。文 [3] 研究得到了方程(1-1)的五类爆破解：双曲爆破解、分数爆破解、三角爆破解、第一椭圆爆破解和第二椭圆爆破解。另外，还发现两个有界孤立解从一个椭圆爆破解分支的现象。

当 $b = 0$ ， $n = 2$ 时，Yang和Liu [4] 研究了式(1-1)的正孤立波和反孤立波的分支和精确解，并发现了

几个新的性质：(i) 当 $k < \frac{1}{2}$ 时，方程中存在周期波，爆破波和双孤立波三种类型的反孤立波分支；(ii) 当 $k \geq \frac{1}{2}$ 时，方程中存在两种类型的孤立波分支：周期波和爆破波，但不存在双孤立波分支；(iii) 有无穷多

个周期轨在一点或两点相交并通过奇点直线，而在某些同宿轨中不存在奇异点。

当 $b = 2$ ， $n = 1$ 时，方程(1-1)就是Camassa和Holm [5] 在1993年发现的CH方程。当 $k = 0$ 时，Camassa和Holm [5] 研究发现CH方程是可积的，并且具有尖波解。Cooper和Shepard [6] 推导出CH方程的一个近似孤立波解。Boyd [7] 导出了一个系列波，它们在波峰处收敛到一个极限，并在CH方程中发现了余弦波。Constantin和Strauss [8] 给出了交互孤立波存在性的数学描述，并证明了 $k = 0$ 时CH方程的波峰是稳定的。

当 $b = 3$ ， $n = 1$ 时，方程(1-1)就成了Degasperisand Procesi [9] 在2002年提出的DP方程。Lundmark和Szmigielski [10] [11] 提出了计算DP方程n波峰解的逆散射方法，并给出了3波峰解的具体表达式。Chen和Tang [12] 证明了DP方程的扭结波的存在性。Guha [13] 得到了DP方程的Euler-Poincare形式。

近年来，定性分析理论 [14] [15] 和动力系统分支方法相继被成功用于非线性方程的研究，前人在 $b = 0$ ， $n \leq 2$ 时关于方程(1-1)做出了很多研究，在本文中，我们用同样的方法，研究方程(1-1)在 $b = 0$ ， $n = 3$ 和 $n = 4$ 时孤立波的存在性和分支情况。

2. 次数为3的分支情况

本节主要讨论次数为3的情形，即方程

$u_{t} + 2 k u_{x} - u_{x x t} + u^{3} u_{x} - u u_{x x x} = 0$ ， (2-1)

对应的行波系统。利用定性分析理论和动力系统分支方法研究行波系统的孤立波分支情况，给出其隐式解。

对式(2-1)变换得到以下行波系统：

${\begin{cases} \frac{d φ}{d ξ} = y \\ \frac{d y}{d ξ} = \frac{f (φ) + \frac{1}{2} y^{2}}{φ - c} \end{cases}$ (2-2)

其中，

$f (φ) = g + (2 k - c) φ + \frac{1}{4} φ^{4}$ ， (2-3)

以及系统对应的首次积分：

$H_{1} (φ, y) = h$ ， (2-4)

其中，

$H_{1} (φ, y) = {(φ - c)}^{- 1} [y^{2} - G_{1} (φ)]$ ， (2-5)

$G_{1} (φ) = \frac{1}{6} [{(φ - c)}^{4} + \frac{3}{2} a_{3} {(φ - c)}^{3} + 3 a_{2} {(φ - c)}^{2} + 3 a_{1} \ln | φ - c | (φ - c) - 3 a_{0}]$ ， (2-6)

${\begin{cases} a_{0} = 4 g + 4 c (2 k - c) + c^{4} \\ a_{1} = 4 (2 k - c + c^{3}) \\ a_{2} = 6 c^{2} \\ a_{3} = 4 c \end{cases}$ (2-7)

注意到h是一个积分常数。进一步，我们可得到以下两条分支曲线：

$g_{1} (c) = \frac{3}{4} \sqrt[3]{{(c - 2 k)}^{4}}$ ， (2-8)

$g_{2} (c) = \frac{1}{4} (4 c^{2} - 8 k c - c^{4})$ ， (2-9)

显然，分支曲线 $g_{1} (c)$ 和 $g_{2} (c)$ 有以下的分支情况：

(i) 当 $k < 0$ 时， $g_{1} (c)$ 和 $g_{2} (c)$ 只有一个分支波速 $c_{1}$ ；

(ii) 当 $k = 0$ 时， $g_{1} (c)$ 和 $g_{2} (c)$ 只有一个分支波速 $c_{1} (c_{1} = 1)$ ；

(iii) 当 $0 < k < \frac{1}{3 \sqrt{3}}$ 时， $g_{1} (c)$ 和 $g_{2} (c)$ 有两个分支波速 $c_{1}$ ， $c_{2}$ ；

(iv) 当 $k = \frac{1}{3 \sqrt{3}}$ 时， $g_{1} (c)$ 和 $g_{2} (c)$ 只有一个分支波速 $c_{1} (c_{1} = \frac{1}{\sqrt{3}})$ ；

(v) 当 $k > \frac{1}{3 \sqrt{3}}$ 时， $g_{1} (c)$ 和 $g_{2} (c)$ 没有分支波速。

根据以上分析，我们可以得到系统(2-2)的分支相图，见图1~5。

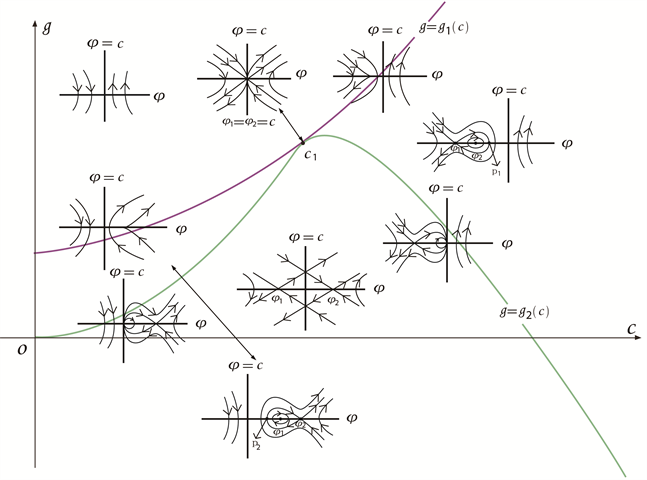
Figure 1. Bifurcation phase portrait of system (2-2) when $k < 0$

图1. $k < 0$ 时，系统(2-2)的分支相图

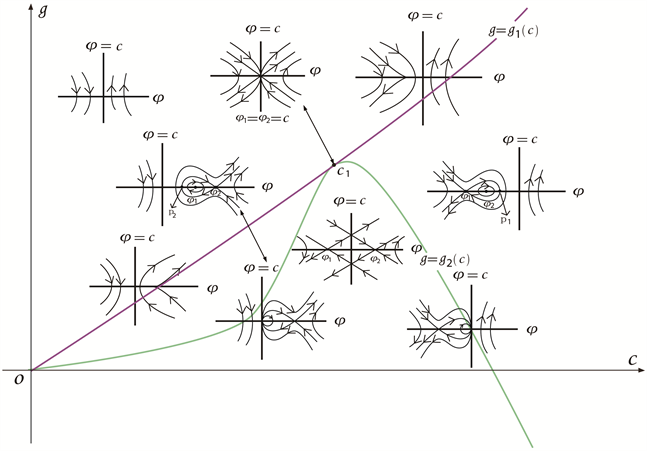
Figure 2. Bifurcation phase portrait of system (2-2) when $k = 0$

图2. $k = 0$ 时，系统(2-2)的分支相图

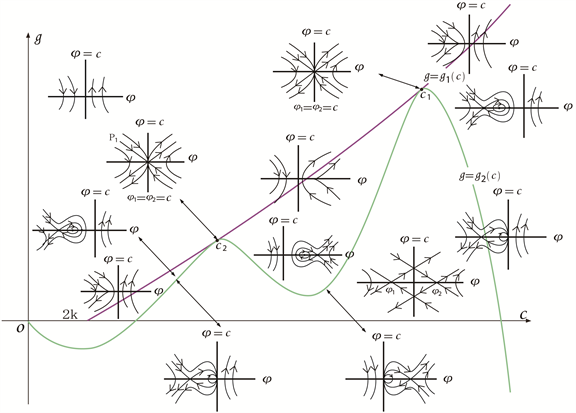
Figure 3. Bifurcation phase portrait of system (2-2) when $0 < k < \frac{1}{3 \sqrt{3}}$

图3. $0 < k < \frac{1}{3 \sqrt{3}}$ 时，系统(2-2)的分支相图

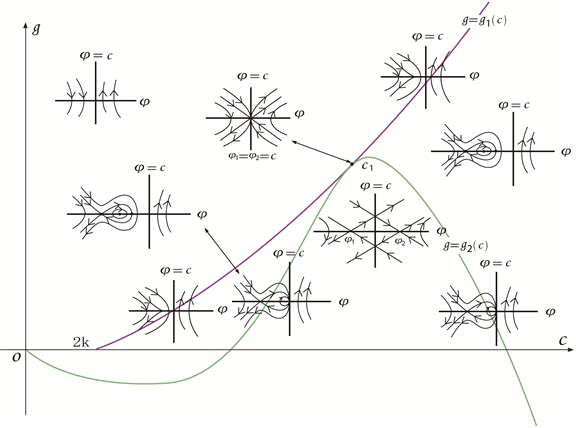
Figure 4. Bifurcation phase portrait of system (2-2) when $k = \frac{1}{3 \sqrt{3}}$

图4. $k = \frac{1}{3 \sqrt{3}}$ 时，系统(2-2)的分支相图

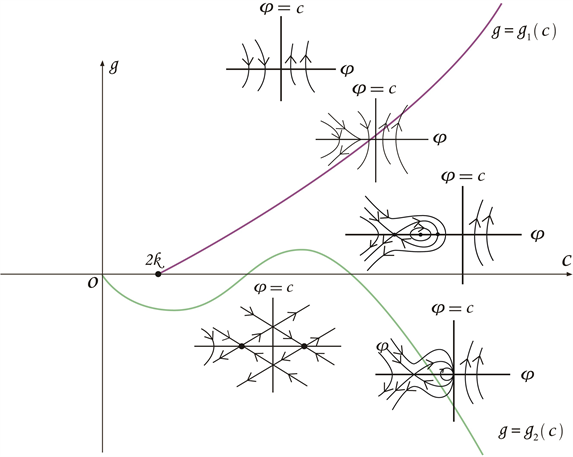
Figure 5. Bifurcation phase portrait of system (2-2) when $k > \frac{1}{3 \sqrt{3}}$

图5. $k > \frac{1}{3 \sqrt{3}}$ 时，系统(2-2)的分支相图

根据图1~5，以及与方程(2-1)相关的行波系统(2-2)，我们研究孤立波的存在性及其分支情况，可得到以下命题：

命题2.1 对于给定的参数k，正波速c和积分常数g，系统(2-2)的孤立波的存在性和分支情况如下：

(I) 在以下几种情况下，行波系统存在着正孤立波：

(I-1) 当 $k \leq 0$ 时， $c > c_{1}$ ， $g_{2} (c) \leq g < g_{1} (c)$ ；

(I-2) 当 $0 < k < \frac{1}{3 \sqrt{3}}$ 时， $2 k < c < c_{1}$ 或 $c > c_{2}$ ， $g_{2} (c) \leq g < g_{1} (c)$ ；

(I-3) 当 $k = \frac{1}{3 \sqrt{3}}$ 时， $2 k < c < c_{1}$ 或 $c > c_{1}$ ， $g_{2} (c) \leq g < g_{1} (c)$ 。

(II) 在以下几种情况下，行波系统存在着反孤立波：

(II-1) 当 $k \leq 0$ 时， $0 < c < c_{1}$ ， $g_{2} (c) \leq g < g_{1} (c)$ ；

(II-2) 当 $0 < k < \frac{1}{3 \sqrt{3}}$ 时， $c_{1} < c < c_{2}$ ， $g_{2} (c) \leq g < g_{1} (c)$ 。

3. 次数为4的分支情况

本节主要讨论次数为4的情形，即方程

$u_{t} + 2 k u_{x} - u_{x x t} + u^{4} u_{x} - u u_{x x x} = 0$ ， (3-1)

对应的行波系统。利用定性分析理论和动力系统分支方法研究行波系统的孤立波分支情况，给出其隐式解。

类似第二节的方法，我们直接给出以下重要式子：

${\begin{cases} \frac{d φ}{d ξ} = y \\ \frac{d y}{d ξ} = \frac{h (φ) + \frac{1}{2} y^{2}}{φ - c} \end{cases}$ (3-2)

$h (φ) = g + (2 k - c) φ + \frac{1}{5} φ^{5}$ ， (3-3)

$H_{2} (φ, y) = h$ ， (3-4)

$H_{2} (φ, y) = {(φ - c)}^{- 1} [y^{2} - G_{2} (φ)]$ ， (3-5)

$G_{2} (φ) = \frac{1}{10} [{(φ - c)}^{5} + \frac{2}{3} b_{4} {(φ - c)}^{4} + b_{3} {(φ - c)}^{3} + 2 b_{2} {(φ - c)}^{2} + 2 b_{1} \ln | φ - c | (φ - c) - 2 b_{0}]$ ， (3-6)

${\begin{cases} b_{0} = 10 g + 10 c (2 k - c) + 2 c^{5} \\ b_{1} = 10 (c^{4} - c + 2 k) \\ b_{2} = 20 c^{3} \\ b_{3} = 20 c^{2} \\ b_{4} = 10 c \end{cases}$ (3-7)

$g_{3} (c) = \frac{4}{5} \sqrt[4]{{(c - 2 k)}^{5}}$ ， (3-8)

$g_{4} (c) = \frac{1}{5} (5 c^{2} - 10 k c - c^{5})$ ， (3-9)

显然，分支曲线 $g_{3} (c)$ ， $g_{4} (c)$ 和 $- g_{3} (c)$ 有以下的分支波速：

(i) 当 $k \leq 0$ 时， $g_{3} (c)$ 和 $g_{4} (c)$ 有一个分支波速 $c_{3}$ ， $g_{4} (c)$ 和 $- g_{3} (c)$ 有一个分支波速 $c_{5}$ ；

(ii) 当 $0 < k < \frac{3}{8 \sqrt[3]{4}}$ 时， $g_{3} (c)$ 和 $g_{4} (c)$ 有两个分支波速 $c_{3}$ ， $c_{4}$ ， $g_{4} (c)$ 和 $- g_{3} (c)$ 有两个分支波速 $c_{5}$ ， $c_{6}$ ；

(iii) 当 $k = \frac{3}{8 \sqrt[3]{4}}$ 时， $g_{3} (c)$ 和 $g_{4} (c)$ 有一个分支波速 $c_{3} (c_{3} = \frac{1}{\sqrt[3]{4}})$ ， $g_{4} (c)$ 和 $- g_{3} (c)$ 有两个分支波速 $c_{5}$ ， $c_{6}$ ；

(iv) 当 $\frac{3}{8 \sqrt[3]{4}} < k < k^{*}$ ， $g_{4} (c)$ 和 $- g_{3} (c)$ 有两个分支波速 $c_{5}$ ， $c_{6}$ ；

(v) 当 $k = k^{*}$ 时， $g_{4} (c)$ 和 $- g_{3} (c)$ 有一个分支波速 $c_{5}$ ；

(vi) 当 $k > k^{*}$ 时，无分支波速。

注意， $k^{*}$ 是 $c_{5} = c_{6}$ 时的参数k值，这里由于次数比较高，无法计算出具体数值。

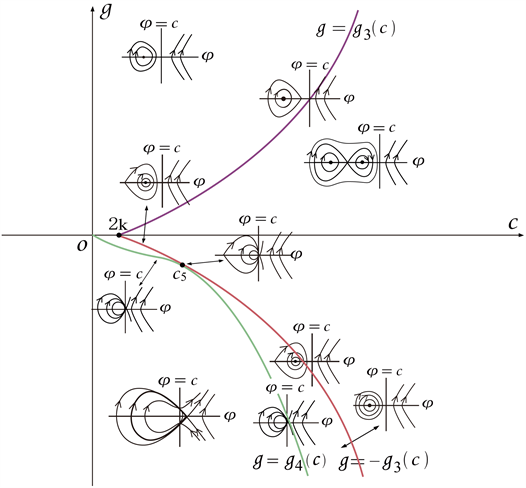
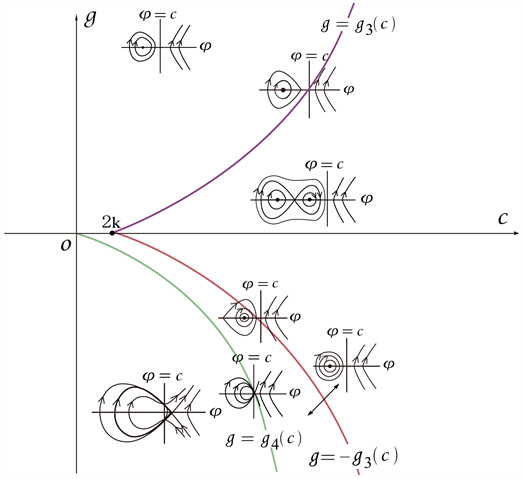
根据以上分析，我们可以得到系统(3-2)的分支相图，见图6~11。

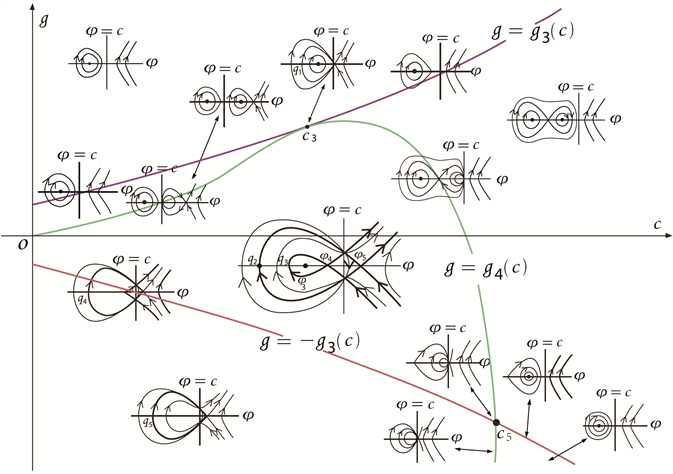
Figure 6. Bifurcation phase portrait of system (3-2) when $k < 0$

图6. $k < 0$ 时，系统(3-2)的分支相图

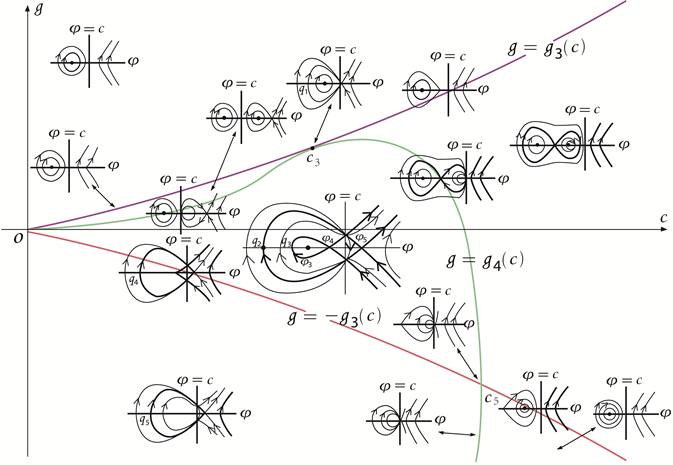
Figure 7. Bifurcation phase portrait of system (3-2) when $k = 0$

图7. $k = 0$ 时，系统(3-2)的分支相图

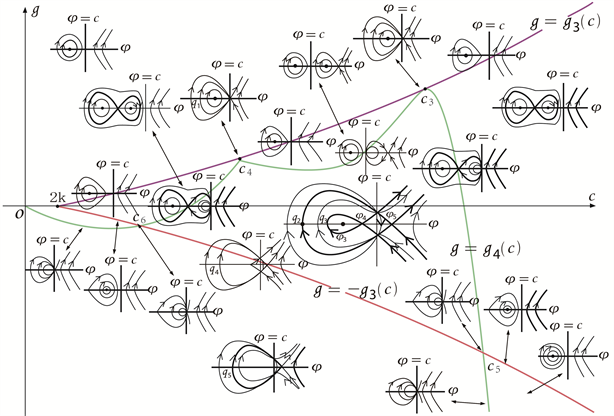
Figure 8. Bifurcation phase portrait of system (3-2) when $0 < k < \frac{3}{8 \sqrt[3]{4}}$

图8. $0 < k < \frac{3}{8 \sqrt[3]{4}}$ 时，系统(3-2)的分支相图

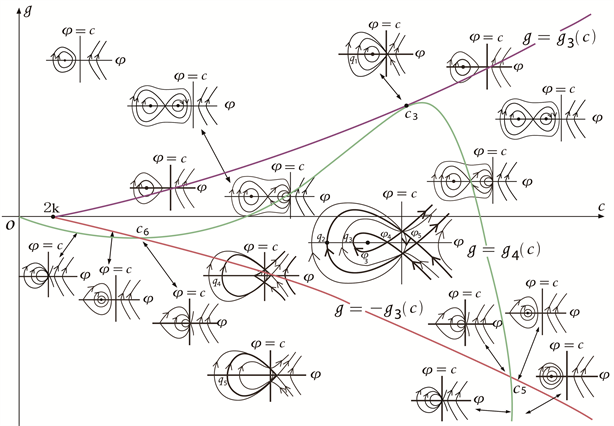
Figure 9. Bifurcation phase portrait of system (3-2) when $k = \frac{3}{8 \sqrt[3]{4}}$

图9. $k = \frac{3}{8 \sqrt[3]{4}}$ 时，系统(3-2)的分支相图

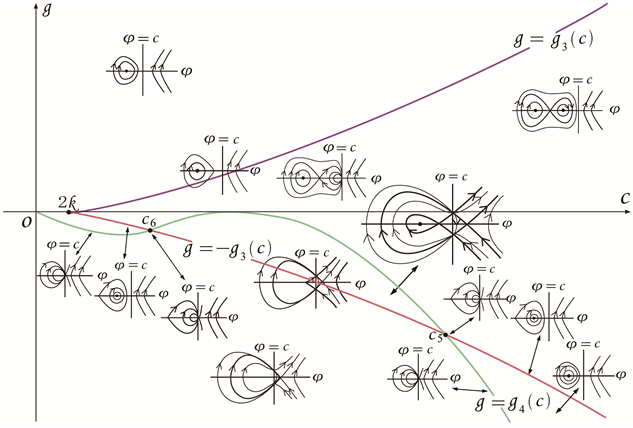
Figure 10. Bifurcation phase portrait of system (3-2) when $\frac{3}{8 \sqrt[3]{4}} < k < k^{*}$

图10. $\frac{3}{8 \sqrt[3]{4}} < k < k^{*}$ 时，系统(3-2)的分支相图

(a) $k = k^{*}$ (b) $k > k^{*}$

Figure 11. Bifurcation phase portrait of system (3-2) when $k \geq k^{*}$

图11. $k \geq k^{*}$ 时，系统(3-2)的分支相图

根据图6~11，以及与方程(3-1)相关的行波系统(3-2)，研究孤立波的存在性和分支情况，可得到以下命题：

命题3.1 对于给定的参数k，正波速c和积分常数g，方程(3-1)的孤立波的存在性如下：

(I) 在以下两种情况下，存在着一个正孤立波：

(A) 当 $k \leq 0$ 时， $c \geq c_{5}$ ， $g = - g_{3} (c)$ ；

(B) 当 $0 < k \leq \frac{1}{3 \sqrt{3}}$ 时， $2 k < c < c_{6}$ 或 $c \geq c_{5}$ ， $g = - g_{3} (c)$ 。

(II) 在以下三种情况下，存在着一个反孤立波：

(C₁) $0 < c < c_{3}$ ， $g_{4} (c) \leq g < g_{3} (c)$ ；

(C₂) $c \geq c_{3}$ ， $g = g_{3} (c)$ ；

(C₃) $0 < c < c_{5}$ ， $g \leq - g_{3} (c)$ ；

(C₄) $0 \geq c_{5}$ ， $g < g_{4} (c)$ ；

(D) 当 $0 < k < \frac{1}{3 \sqrt{3}}$ 时，以下四种情况成立：

(D₁) $2 k < c \leq c_{4}$ 或 $c \geq c_{3}$ ， $g = g_{3} (c)$ ；

(D₂) $c_{4} < c < c_{3}$ ， $g_{4} (c) \leq g < g_{3} (c)$ ；

(D₃) $0 < c \leq c_{6}$ 或 $c \geq c_{5}$ ， $g < g_{4} (c)$ ；

(D₄) $c_{6} < c < c_{5}$ ， $g \leq - g_{3} (c)$ ；

(E) 当 $k = \frac{1}{3 \sqrt{3}}$ 时，以下几种情况成立：

(E₁) $c > 2 k$ ， $g = g_{3} (c)$ ；

(E₂) $0 < c \leq c_{6}$ 或 $c \geq c_{5}$ ， $g < g_{4} (c)$ ；

(E₃) $c_{6} < c < c_{5}$ ， $g \leq - g_{3} (c)$ 。

(III) 在以下三种情况下，存在着一个正孤立波和一个反孤立波：

(F) 当 $k \leq 0$ 时，以下两种情况成立：

(F₁) $c_{3} < c < c_{5}$ ， $g_{4} (c) \leq g < g_{3} (c)$ ；

(F₂) $c \geq c_{5}$ ， $| g | < g_{3} (c)$ ；

(G) 当 $0 < k < \frac{1}{3 \sqrt{3}}$ 时，以下几种情况成立：

(G₁) $2 k < c < c_{6}$ 或 $c \geq c_{5}$ ， $| g | < g_{3} (c)$ ；

(G₂) $c_{6} < c < c_{4}$ 或 $c_{3} < c < c_{5}$ ， $g_{4} (c) \leq g < g_{3} (c)$ ；

(H) 当 $k = \frac{1}{3 \sqrt{3}}$ 时，以下几种情况成立：

(H₁) $2 k < c < c_{6}$ 或 $c \geq c_{5}$ ， $| g | < g_{3} (c)$ ；

(H₂) $c_{6} < c < c_{3}$ 或 $c_{3} < c < c_{5}$ ， $g_{4} (c) \leq g < g_{3} (c)$ 。

(IV) 在以下两种情况下，存在着两个反孤立波：

(I) $k \leq 0$ ， $0 < c \leq c_{3}$ ， $- g_{3} (c) < g < g_{4} (c)$ ；

(J) $0 < k \leq \frac{1}{3 \sqrt{3}}$ ， $c_{6} < c \leq c_{5}$ ， $- g_{3} (c) < g < g_{4} (c)$ 。

文章引用

邹玲玲,刘锐. 一类高次非线性方程的孤立波分支
Bifurcations of Solitary Waves for a Class of Higher Order Nonlinear Equations[J]. 应用数学进展, 2020, 09(08): 1273-1285. https://doi.org/10.12677/AAM.2020.98149

参考文献

1. Yang, J.P., Li, Z.G. and Liu, Z.R. (2018) The Existence and Bifurcation of Peakon and Anti-Peakon to Then-Degree B-Equation. International Journal of Bifurcation and Chaos, 28, Article ID: 1850014. https://doi.org/10.1142/S0218127418500141

2. Li, Z.G. and Liu, R. (2019) Bifurcations and Exact Solutions in a Nonlinear Wave Equation. International Journal of Bifurcation and Chaos, 29, Article ID: 1950098. https://doi.org/10.1142/S0218127419500986

3. Li, Z.G. and Liu, R. (2020) Blow-Up Solutions for a Class of B-Family Equations. Acta Mathematica Scientia, 40, 910-920. https://doi.org/10.1007/s10473-020-0402-4

4. Yang, J.P., Liu, R. and Chen, Y.R. (2020) Bifurcations of Solitary Waves of a Simple Equation. International Journal of Bifurcation and Chaos, 30, Article ID: 2050138. https://doi.org/10.1142/S0218127420501382

5. Camassa, R. and Holm, D.D. (1993) An Integrable Shallow Water Equation with Peaked Solitons. Physical Review Letters, 71, 1661-1664. https://doi.org/10.1103/PhysRevLett.71.1661

6. Cooper, F. and Shepard, H. (1994) Solitons in the Camassa-Holm Shallow Water Equation. Physics Letters A, 194, 246-250. https://doi.org/10.1016/0375-9601(94)91246-7

7. Boyd, J.P. (1997) Peakons and Coshoidal Waves: Travelling Wave Solutions of the Camassa-Holm Equation. Applied Mathematics and Computation, 81, 173-187. https://doi.org/10.1016/0096-3003(95)00326-6

8. Constantin, A. and Strauss, W.A. (2000) Stability of Peakons. Communications on Pure and Applied Mathematics, 53, 603-610. https://doi.org/10.1002/(SICI)1097-0312(200005)53:5<603::AID-CPA3>3.0.CO;2-L

9. Degasperis, A. and Procesi, M. (1999) Asymptotic Integrability. In: Degasperis, A. and Gaeta, G., Eds., Symmetry and Perturbation Theory, World Scientific, Singapore, 23-37. https://doi.org/10.1142/9789812833037

10. Lundmark, H. and Szmigielski, J. (2003) Multi-Peakon Solutions of the Degasperis-Procesi Equation. Inverse Probability, 19, 1241-1245. https://doi.org/10.1088/0266-5611/19/6/001

11. Lundmark, H. and Szmigielski, J. (2005) Degasperis-Procesi Peakons and the Discrete Cubic String. International Mathematics Research Papers, 2, 53-116. https://doi.org/10.1155/IMRP.2005.53

12. Chen, C. and Tang, M.Y. (2006) A New Type of Bounded Waves for Degasperis-Procesi Equations. Chaos, Solitons & Fractals, 27, 698-704. https://doi.org/10.1016/j.chaos.2005.04.040

13. Guha, P. (2007) Euler-Poincare Formalism of (Two Component) Degasperis-Procesi and Holm-Staley Type Systems. Journal of Nonlinear Mathematical Physics, 14, 398-429. https://doi.org/10.2991/jnmp.2007.14.3.8

14. 刘正荣. 微分方程定性方法和数值模拟[M]. 广州: 华南理工出版社, 2013.

15. 张芷芬, 丁同仁, 黄文灶, 等. 微分方程定性理论[M]. 北京: 广东高等教育出版社, 1995.

期刊菜单