Advances in Applied Mathematics
Vol.
09
No.
10
(
2020
), Article ID:
38361
,
8
pages
10.12677/AAM.2020.910211
过指定顶点的三次B样条曲线及其应用
白根柱1,2
1浙江长征职业技术学院基础部,浙江 杭州
2内蒙古民族大学数理学院,内蒙古 通辽
收稿日期:2020年10月7日;录用日期:2020年10月21日;发布日期:2020年10月28日

摘要
本文构造了通过给定控制多边形指定顶点且与始末控制多边形的始末边相切的两段连续三次B样条曲线,并以此两段连续的三次B样条曲线为轴线的管道光滑拼接了轴线异面椭圆管道。该方法相较于三段连续的三次均匀B样条曲线为轴线的管道、插值于两端点并与控制多边形的始末边相切的三次有理B样条曲线为轴线的管道、两段连续二次B样条曲线为轴线的管道光滑拼接轴线异面管道,各有其优越性。具有理论意义和应用价值。
关键词
B样条,分段连续,光滑拼接,轴线异面,椭圆管道
Cubic B-Spline Curve of Passing Appointed Vertexes and Its Application
Genzhu Bai1,2
1Basis Department, Zhejiang Changzheng Vocational & Technical College, Hangzhou Zhejiang
2College of Mathematics and Physics, Inner Mongolia University for the Nationalities, Tongliao Inner Mongolia

Received: Oct. 7th, 2020; accepted: Oct. 21st, 2020; published: Oct. 28th, 2020

ABSTRACT
In this paper, we construct continuous two-section of cubic B-spline curve which is tangent to the start and end points of the control polygon. And we construct a tube that smoothly blends two ellipse tubes whose axes non-coplanar with the two continuous cubic B-spline curves as its axes. The results show that the method is better than that in which tubes are smoothly blended between smoothly connected three-segment tubes with cubic uniform B-spline curves as its axis, and tubes are smoothly blended by tube whose axis is a cubic rational B-spline curve interpolated at both ends and tangent to the start and end edges of the control polygon, and tubes are smoothly blended between smoothly connected two-segment tubes and quadratic uniform B-spline curves as its axis, which has theoretical significance and application value.
Keywords:B-Spline, Piecewise Continuous, Smooth Blending, Non-Coplaner, Elliptic Tube

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
轴线异面管道光滑拼接问题研究是计算几何领域中难点基础问题。我们提出基于轴线光滑拼接的轴线异面管道光滑拼接技术旨在构造更多的自由曲线来光滑拼接轴线异面管道的轴线,进而实现两个轴线异面的管道的光滑拼接。Bézier曲线具有很好的端点性质,但是不具有局部修改性质。人们尝试将具有很好的局部修改性质的B样条曲线也具有像Bézier曲线那样很好的端点性质。主要通过两个途径,一种是对于 为控制多边形顶点的三次B样条曲线在原来控制多边形的始末两段再增加两个顶点 和 ,满足 和 ,使B样条曲线通过原来控制多边形的起点 和终点 ;另一种是对于给定的以 为顶点的控制多边形构造过指定顶点的三次B样条曲线,反算B样条曲线的实际控制顶点 。由于B样条曲线是分段光滑曲线,增加顶点会增加分段曲线的段数。构造插值于两端点的B样条曲线,并要求分段光滑曲线的段数较少,可能由于约束条件较少,构造出来的B样条曲线的光顺性不够理想。我们在文献 [1] 中用增加顶点的方法构造了三段连续的三次B样条曲线,用于轴线光滑拼接的轴线异面管道的拼接。在文献 [2] 中,对于给定的控制顶点,尝试用一段三次B样条曲线光滑拼接轴线异面管道的轴线,并将其应该用于轴线异面管道光滑拼接,发现光顺性较差,改用一段三次有理B样条曲线,并将其应该用于轴线异面圆管道光滑拼接。在选取权因子调整轴线的形状时,两端点附近的切线发生急剧变化,致使不能应用于轴线异面椭圆管道的拼接中。而在文献 [3] 中,对于给定的一段三次B样条曲线的控制顶点 ,利用二次B样条曲线与控制多边形的两边相切并通过控制多边形中点这一特性,构造了两段连续的二次B样条曲线,并将其应用于轴线异面管道光滑拼接。由于二次B样条曲线是平面曲线,而轴线异面管道的轴线不在同一平面内,造成连接点处的切线不连续,在构造光滑拼接的椭圆管道时需要反复调整椭圆管道的长半轴和短半轴才能实现,且曲线只能过控制多边形的边 的中点。本文对于给定
控制多边形顶点 ,在 和 中间插入一个顶点 ,构造两段连续的三次B样条曲线过指定顶点 和 ,与始末两条边相切,并将其应用于轴线异面椭圆管道拼接中。
2. 过指定顶点的三次B样条曲线
在轴线异面管道拼接中,假设管道轴线 和 是异面直线, 位于空间直角坐标系XOY平面内且与Y轴平行, 位于YOZ平面内且与Y轴相交,连接 和 两点构成以 为控制顶点
的控制多边形。为了构造两段连续的三次B样条曲线,在 和 中间插入一个顶点 构成以 为顶点的控制多边形。
定义1设
是三次均匀B样条函数。其中 为三次均匀B样条基, 为特征多边形的顶点。
令 。下面构造插值于 ,并在 处与 相切,在 处与 相切的两段连续三次B样条曲线,需满足:
解以 为变量的线性方程组,得
于是,所求两段连续的三次B样条曲线的表达式为
例1设 ,适当选取 ,调整三次B样条曲线的形状。
1) 取 ,得以 为控制顶点,并过 ,且在 处与 相切,在 处与 相切的两段连续三次B样条曲线,其参数表达式
如图1。
2) 取 ,得以 为控制顶点,过点 ,并在 处与 相切,在 处与 相切的两段连续三次B样条曲线,其参数表达式为
如图1。
3) 取 ,得以 为控制顶点,过点 ,并在 处与 相切,在 处与 相切的两段连续三次B样条曲线,其参数表达式为
如图1。
将 上述三种取值时得到的三条两段连续的三次B样条曲线放在一起,如图2。
可以取多种值,利用B样条曲线的局部修改性质可得满足应用条件的轴线应用于轴线异面管道拼接中。

Figure 1. Connection between continuous two-section of cubic B-spline curves and axis when taking three-different values for
图1. 为 取三种不同值时两段连续的三次B样条曲线与轴线连接情况

Figure 2. When takes three different values, three continuous two-section of cubic B-spline curves are put together
图2. 为 取三种不同值时三条两段连续的三次B样条曲线放在一起的情况
3. 过指定顶点的三次B样条曲线及其在轴线异面椭圆管道拼接中的应用
我们利用三次B样条曲线的局部修改性质,构造了过指定顶点的两段连续的三次B样条曲线,曲线通过控制多边形的两端点并与始末两边相切,而曲线的形状可由第三个指定顶点的位置来调控。这样,我们可将其应用于轴线光滑拼接的轴线异面管道拼接中 [4] [5]。
例2设 和 分别是长半轴和短半轴分别相同的两个椭圆管道,其参数表达式为
和
其中 是轴线的参数表达式,取三次B样条曲线的控制多边形的顶点为 ,则两段连续的三次B样
条曲线的表达式为例1(3)。构造基于两段连续的轴线光滑拼接的两段椭圆管道,其参数表达式为
和
其中 和 分别是连续两段B样条曲线的主法矢和副法矢与 和 的拼接效果如图3。

Figure 3. When ,, the effect drawing is obtained by given elliptic tubes whose axes are in non-coplaneris blended by two sections of constructed elliptic tubes of smooth blending
图3. , 时,构造的两段光滑拼接的椭圆管道与给定轴线异面椭圆管道拼接效果图
椭圆管道拼接不同于圆管道。在构造椭圆管道时,轴线上每一点处与轴线垂直的平面上的自然坐标系 上构造椭圆,椭圆的长半轴和短半轴的方向与主法矢和副法矢的方向相关。例2中, 与 的长半轴与短半轴是相对应的,而 与 的长半轴与短半轴是不相对应的。在 每一点 处对 坐标轴旋转变换
其中 , 为 (或 )与 长半轴(或短半轴)夹角, 为 (或 )与 长半轴(或短半轴)夹角。调整后的拼接效果如图4。
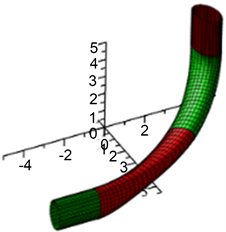
Figure 4. When ,, the effect drawing is obtained by given elliptic tubes whose axes are in non-coplaneris blended by two sections of adjusted elliptic tubes of smooth blending
图4. , 时,调整后两段光滑拼接的椭圆管道与给定轴线异面椭圆管道光滑拼接效果图
当 时,还可以构造两段光滑拼接的椭圆管道光滑拼接轴线异面的椭圆管道 [5]。
例3设 和 分别是长半轴和短半轴分别不同的两个椭圆管道,其参数表达式为
和
光滑拼接两个异面轴线的两段连续三次B样条曲线如例1 (3)。构造光滑拼接两个轴线异面椭圆管道某一母线的两段连续三次B样条曲线为
光滑拼接两个轴线异面椭圆管道的两段椭圆管道的参数表达式为
其中 和 ,为轴线上互为垂直的单位向量, ,,,。其拼接效果如图5。

Figure 5. Two elliptical tubes whose axes are in non-coplaner and are semi-major axisshort half axis are different from each other are blended by two sections of elliptic tubes of smooth blending
图5. 两个长半轴和短半轴互不相同的轴线异面椭圆管道光滑拼接效果图
图5中, 分别为
和
4. 结束语
用指定顶点的两段连续三次B样条曲线为轴线的两段光滑拼接的椭圆管道拼接两个轴线异面的椭圆管道,与三段连续的三次B样条曲线为轴线的三段光滑拼接的管道拼接两个轴线异面管道相比较段数少,与插值于两端点的三次有理B样条曲线相比较能够构造椭圆管道拼接,而与二次B样条曲线为轴线的管道光滑拼接轴线异面管道相比较能够调整轴线的位置。具有理论意义和较好的应用价值。
基金项目
国家自然科学基金项目资助(11561052),浙江省教育厅一般项目资助Y (201636628)。
文章引用
白根柱. 过指定顶点的三次B样条曲线及其应用
Cubic B-Spline Curve of Passing Appointed Vertexes and Its Application[J]. 应用数学进展, 2020, 09(10): 1821-1828. https://doi.org/10.12677/AAM.2020.910211
参考文献
- 1. 白根柱. 基于轴线光滑拼接的轴线异面管道拼接技术[J]. 应用数学进展, 2019, 8(7): 1267-1271.
- 2. 白根柱. 三次有理B样条曲线及其应用[J]. 应用数学进展, 2020, 9(8): 1331-1337.
- 3. 王芳, 白根柱. 二次B样条曲线及其应用[J]. 湖北民族大学学报(自然科学版), 2020, 38(2): 209-213.
- 4. 乌仁高娃, 陶吐格, 白根柱. Hartmann函数在椭圆管道拼接中的应用[J]. 应用数学进展, 2019, 8(11): 1700-1707.
- 5. Bai, G., Wu, Z. and Lin, X. (2017) Intersecting Line of Conical Surface and Smoothly Blending of Two Tubes Whose Axes Are Non-Coplanar. Journal of Applied Mathematics and Physics, 5, 1887-1991. https://doi.org/10.4236/jamp.2017.59158