Finance
Vol.06 No.02(2016), Article ID:17377,10
pages
10.12677/FIN.2016.62007
Pricing Multi-Period Return Guarantees Combined with Asset Allocation Strategy under Fractional Brownian Motion
Yanlian Deng, Yunsheng Lun
Department of Mathematics, Donghua University, Shanghai
Received: Apr. 3rd, 2016; accepted: Apr. 14th, 2016; published: Apr. 21st, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we consider that the price processes of risky assets are driven by fractional Brownian motion ( ). With the Wick-Itô integral and the quasi-conditional expectation, we compute the value of multi-period return guarantees under CM strategy and under CPPI strategy. Through the numerical simulation, the influence on the value of multi-period return guarantees under the two strategies is compared and analyzed, which is made by the periods of multi-period return guarantees and the important parameters of the financial market and asset allocation strategy.
). With the Wick-Itô integral and the quasi-conditional expectation, we compute the value of multi-period return guarantees under CM strategy and under CPPI strategy. Through the numerical simulation, the influence on the value of multi-period return guarantees under the two strategies is compared and analyzed, which is made by the periods of multi-period return guarantees and the important parameters of the financial market and asset allocation strategy.
Keywords:Fractional Brownian Motion, Quasi-Conditional Expectation, CM Strategy, CPPI Strategy

分数布朗运动环境下的资产配置策略多期收益保证价值的测算
邓艳莲,陆允生
东华大学数学系,上海

收稿日期:2016年4月3日;录用日期:2016年4月14日;发布日期:2016年4月21日

摘 要
本文考虑Hurst指数大于二分之一的分数布朗运动驱动的风险性资产价格过程,结合Wick-Itô积分和拟条件期望,讨论了分数布朗运动环境下结合CM策略和CPPI策略的多期收益保证价值,通过数值模拟,比较分析了多期保证期限、金融市场重要参数和资产配置策略参数对两策略下多期保证价值的影响。
关键词 :分数布朗运动,拟条件期望,CM策略,CPPI策略

1. 引言
风险和投资是金融市场两大不可分割的主题。目前,随着全球金融市场波动性的加剧,越来越多的投资者更倾向于回避风险,追求收益的投资理念,他们期望在市场价格上升时,能获得一定的收益;在市场价格下跌时,又能保证投资头寸的安全。传统的投资理财工具无法满足投资者的这一需求,而以收益保证为特点的新金融产品(下文中称收益保证型金融产品)降低了风险,增加了收益的组合方式,正符合投资者的这一投资理念,因而受到了广大投资者的青睐。
收益保险型金融产品的核心思想是投资机构向投资者提供的收益保证,也相当于卖给投资真一个期权,对投资机构来说则相当于拥有一项或有负债,故存在到期日因收益保证导致的偿付能力不足的风险。因此对收益保证型金融产品投资机构来说,测算收益保证的价值,即或有负债的价值具有十分重要的意义。Brennan和Schwartz [1] 指出,通常情况下,投资机构可以决策采取哪种资产配置策略,于是可以通过采取某种避险策略来降低或规避期末不能偿付收益保证的风险,即降低测算出的收益保证价值。最近,有学者研究了资产配置策略下收益保证价值的测算方法,见张飞、刘海龙 [2] 与王亦奇、刘海龙 [3] 。但他们的研究是建立于经典的Black-Scholes市场模型的框架下(见Black and Scholes [4] )。
在经典的Black-Scholes模型中,假设风险资产的价格过程是布朗运动驱动的随机微分方程。但大量的金融实证研究表明,金融资产的收益率呈现出尖峰厚尾的分布特点,且资产价格呈现出长程相关性Shiryaev [5] ,这并不符合布朗运动的特性。为了准确描述波动的长程相关性,很多学者用分数布朗运动
替换标准布朗运动来研究金融问题。但当 时,分数布朗运动既不是马氏过程,也不是半鞅,这使
时,分数布朗运动既不是马氏过程,也不是半鞅,这使
得经典的随机积分理论无法对其进行分析。为此,以Roger [6] 为代表定义了分数轨道积分(fractional pathwise integrals);Cheridito等 [7] - [9] 指出Black-Scholes模型在分数轨道积分意义下的存在套利,因此分数轨道积分不适用于金融领域的研究。Hu-Øksendal [10] 基于Wick积(Wick product)建立了分数Itô积分和分数Black-Scholes模型,并指出分数Black-Scholes市场是完备的。Necula [9] 通过引入拟鞅定价方法推出了分数Itô积分意义下的分数Black-Scholes公式。虽然Biagini-Hu [11] 通过引入市场观察者的概念指出在Wick自融资和Wick资产组合价值概念下,分数Black-sholes定价模型存在弱套利;Björk-Hult [7] 也指出Wick资产组合价值和Wick自融资概念只能视为纯数学概念,并没有合理的经济学解释,但这至今仍存在很大的争议。随后,Rostek-Schobel [12] 讨论了市场微观模型,指出:若市场参与者都是活跃的,则价格过程服从几何布朗运动;若市场参与者表现出惰性,则价格过程趋向于几何分数布朗运动,且在这两种情况下市场都无套利。基于此,在分数布朗运动的环境下研究金融问题既有理论意义,也有实际意义。
本文结构安排如下:在第2节,我们介绍相关准备知识,主要包括分数布朗运动与金融市场。第3节给出CM资产配置策略和CPPI资产配置策略下收益保证价值的测算方法。在第4节我们给出一些数值模拟与分析。
2. 准备知识
2.1. 分数布朗运动
为了方便表达,我们首先重述相关概念。设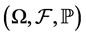 为一概率空间,
为一概率空间,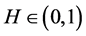 为常数,具有Hurst参数H的分数布朗运动是一个连续高斯过程
为常数,具有Hurst参数H的分数布朗运动是一个连续高斯过程 使得
使得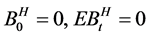 ,且
,且
 ,
,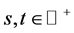 ,
,
显然,当 时,为标准布朗运动,记为Bt。对任意的
时,为标准布朗运动,记为Bt。对任意的 ,记
,记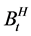 的自相关函数为
的自相关函数为
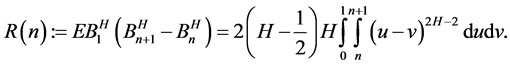
当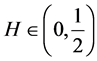 时,
时,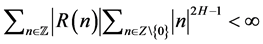 ,称分数布朗运动
,称分数布朗运动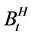 是短记忆的;当
是短记忆的;当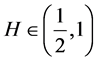 ,
,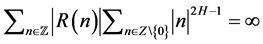 ,称分数布朗运动
,称分数布朗运动 是长记忆的。
是长记忆的。
本文仅考虑 的情形。
的情形。
引入Hermite多项式
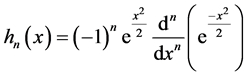 ,
,
定义
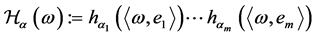 ,
,
其中,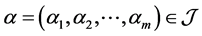 ,
, 表示有限维非负整数指标集。
表示有限维非负整数指标集。
引入下面的对偶空间:
(1) 为分数Hida检验泛函空间,若对任意的
为分数Hida检验泛函空间,若对任意的 有
有
 ,
,
使得对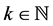 ,
,
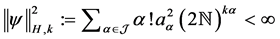 ,
,
其中, ,
,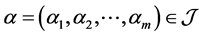 。
。
(2)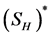 为分数Hida分布空间,若对任意的
为分数Hida分布空间,若对任意的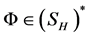 都具有如下展开形式:
都具有如下展开形式:
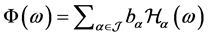 ,
,
使得存在 ,
,
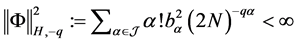 。
。
令 ,满足对任意的
,满足对任意的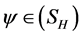 ,有
,有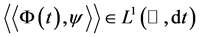 ,则存在唯一的
,则存在唯一的 使得对任意的
使得对任意的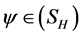 ,
,
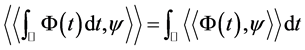 (1)
(1)
其中, ,
, ,若(1)成立,则称
,若(1)成立,则称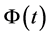 是
是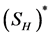 可积的。
可积的。
令 ,
,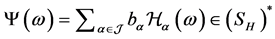 ,定义Wick积如下:
,定义Wick积如下:
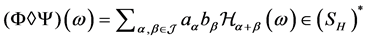 。
。
令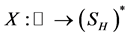 ,
,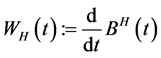 为分数白噪声,若
为分数白噪声,若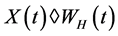 是
是 可积的,则X的分数Wick-Itô积分定义为:
可积的,则X的分数Wick-Itô积分定义为:
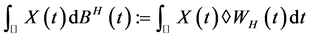 。
。
引入重积分:
 。
。
称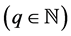
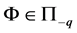 ,若
,若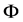 可表示为
可表示为
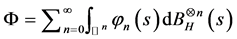 ,
,
且使得
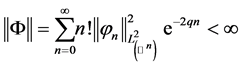 。
。
令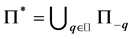 ,定义
,定义 关于自然域流
关于自然域流 的拟条件期望为:
的拟条件期望为:
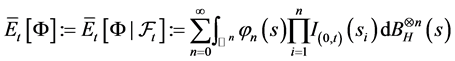 。
。
引理1:(分数拟鞅定价公式)
假设 为风险中性测度,
为风险中性测度,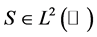 是有界
是有界 可测的未定权益,则在任意时刻
可测的未定权益,则在任意时刻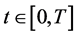 的价格为:
的价格为:
 。
。
2.2. 金融市场
考虑概率空间 上的无摩擦连续金融市场,市场中存在保守性资产和风险性资产。设保守性资产为零息票债券,价格过程
上的无摩擦连续金融市场,市场中存在保守性资产和风险性资产。设保守性资产为零息票债券,价格过程 满足:
满足:
 .
.
考虑风险性资产价格由分数布朗运动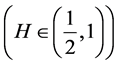 驱动,则价格过程
驱动,则价格过程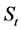 满足:
满足:
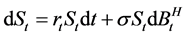 。
。
[6] 中指出,在分数Black-Scholes市场中虽然不存在等价鞅测度,但存在唯一的等价测度 ,即风险中性测度。上式中的市场瞬时无风险利率
,即风险中性测度。上式中的市场瞬时无风险利率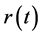 由Vasicek模型刻画,即
由Vasicek模型刻画,即 满足:
满足:
 ,
,
其中,a,b,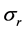 均为常数,
均为常数,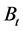 是概率空间
是概率空间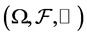 上的标准一维布朗运动。
上的标准一维布朗运动。
若投资资产组合是自融资的,则在风险中性测度 下,设投资于风险性资产的比例(策略函数)为
下,设投资于风险性资产的比例(策略函数)为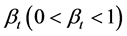 ,则t时刻投资资产组合的价值
,则t时刻投资资产组合的价值 满足:
满足:
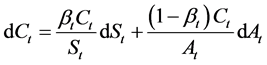 .
.
2.3. 多期收益保证水平的设定
根据收益保证水平的设定,可以将收益保证分为绝对收益保证与相对收益保证。绝对收益保证是将收益保证水平设定为一个固定的常数,而相对收益保证的收益保证水平通常与某一资产或资产组合的收益率挂钩,如证券指数、国债利率等。由于我国金融市场当前的发展尚不完善,所以相对收益保证水平更适用于我国。本文以市场瞬时无风险利率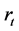 为收益保证水平的挂钩收益率。令第i期的收益保证水平
为收益保证水平的挂钩收益率。令第i期的收益保证水平 为
为
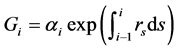 ,
, ,
,
其中, 为第i期的收益保证水平参数,通常
为第i期的收益保证水平参数,通常 。
。
设收益保证的投资期限为T年,每年兑现n次收益保证。假设期初的投资额为 ,记
,记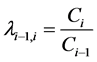 ,
,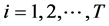 为第i期资产组合的收益率。根据 [3] 中的收益保证价值的测算方法,多期收益保证的支付可以被表示如下
为第i期资产组合的收益率。根据 [3] 中的收益保证价值的测算方法,多期收益保证的支付可以被表示如下
 ,
,
其中,等号是由于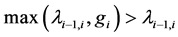 ,即
,即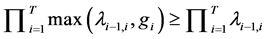 。
。
根据分数拟鞅定价理论,在测度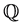 下,多期收益保证的价值为
下,多期收益保证的价值为
 , (2)
, (2)
其中,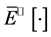 表示风险中性测度
表示风险中性测度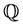 下的拟条件期望。
下的拟条件期望。
3. 资产配置策略
3.1. CM策略
当投资于风险性资产的比例(策略函数)始终为一个固定常数k,即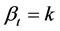 时,我们称资产配置策略为固定组合策略(constant-mix),简称为CM策略。此时,t时刻投资资产组合
时,我们称资产配置策略为固定组合策略(constant-mix),简称为CM策略。此时,t时刻投资资产组合 满足
满足
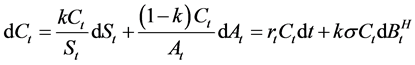 。 (3)
。 (3)
定理1
当资产配置策略为CM策略时,多期收益保证的价值V为
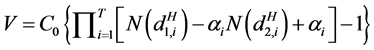 .
.
其中, 为正态分布函数,
为正态分布函数, ,
, 。
。
证明:在 空间下重写(3)得
空间下重写(3)得
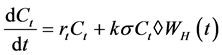 。
。
由Wick-Itô积分可知
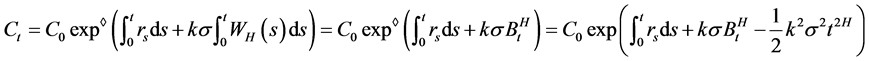 (4)
(4)
由(4)式可知,第i期资产组合的收益率为
 。
。
令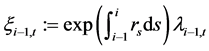 ,则根据Wick-Itô积分易知,
,则根据Wick-Itô积分易知,
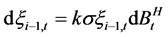 。
。
显然,在风险中性测度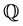 下,
下,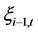 服从飘移项为0,波动率为
服从飘移项为0,波动率为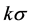 的几何分数布朗运动。于是,
的几何分数布朗运动。于是,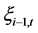 可看成短期利率为0的金融市场上初始价值为1的风险性资产。根据分数布朗运动环境下的期权定价结果,
可看成短期利率为0的金融市场上初始价值为1的风险性资产。根据分数布朗运动环境下的期权定价结果,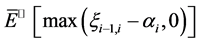 可视为初始资产价格为
可视为初始资产价格为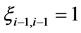 ,执行价格为
,执行价格为 ,持续期为1,无风险利率为0,波动率为
,持续期为1,无风险利率为0,波动率为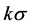 的欧式看涨期权的价值。根据分数Black-Scholes公式可知,
的欧式看涨期权的价值。根据分数Black-Scholes公式可知,
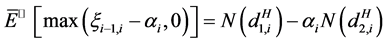 ,
,
其中, 为正态分布函数,
为正态分布函数,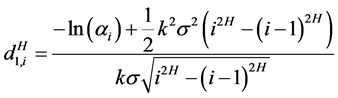 ,
, 。
。
由(2)式可知
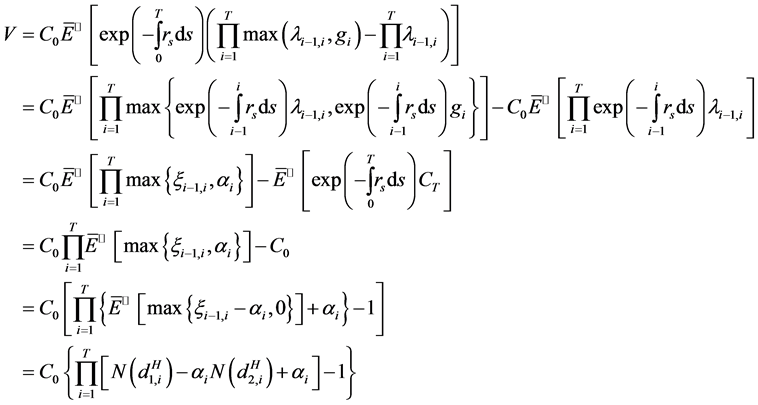 ,
,
其中,第4个等号基于分数拟鞅定价公式。
3.2. CPPI策略
1987年,Black和Jones最先提出固定比例投资组合保险策略(constant proportion portfolio insurance),简称CPPI策略。目前,CPPI策略以模型简单,参数的设定能充分反映不同投资人的风险偏好,且易于操作与实施等特点备受大型收益保证性金融产品投资机构的青睐。当资产配置策略为CPPI策略时,投资于风险性资产的比例(策略函数)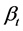 与t时刻资产组合的市场价值
与t时刻资产组合的市场价值 相关,即
相关,即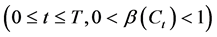
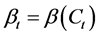 ,则
,则
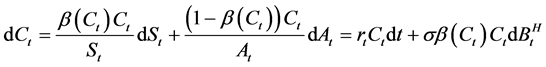 。
。
在时点 ,
,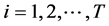 ,CPPI策略的价值底线
,CPPI策略的价值底线 为
为
 ,
,
则缓冲额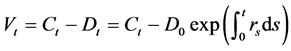 。CPPI策略的核心思想是在t时刻,将
。CPPI策略的核心思想是在t时刻,将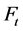 的资金投资于风险性资产,其余部分投资于保守型资产。
的资金投资于风险性资产,其余部分投资于保守型资产。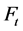 可表示如下:
可表示如下:
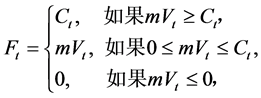
其中, 为策略乘数。易知
为策略乘数。易知 ,则该策略下资产组合t时刻的价值
,则该策略下资产组合t时刻的价值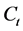 满足
满足
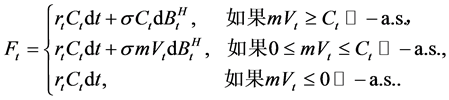
由于CPPI策略下资产组合的市值 是分段函数,不易求得其解析解,所以也很难求得收益保证价值V的解析解,因此我们将力求数值解。数值模拟方法:分别模拟10,000条资产组合价值
是分段函数,不易求得其解析解,所以也很难求得收益保证价值V的解析解,因此我们将力求数值解。数值模拟方法:分别模拟10,000条资产组合价值 路径和10,000条瞬时利率
路径和10,000条瞬时利率 路径,每条模拟路径分为200步,则每条路径都将有不同的收益率,不同的贴现水平等等,然后将所有模拟路径下得到的结果求平均值,即可得到收益保证价值V的数值解。
路径,每条模拟路径分为200步,则每条路径都将有不同的收益率,不同的贴现水平等等,然后将所有模拟路径下得到的结果求平均值,即可得到收益保证价值V的数值解。
4. 数值分析
本节将通过数值分析来验证上述测算方法的可行性和有效性,并比较分析收益保证水平,风险资产波动率,保证期限及资产配置策略参数对两策略下多期收益保证价值的影响。为了便于比较,我们假定收益保证水平参数 为与i无关的常数,并令
为与i无关的常数,并令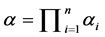 。模拟采用的参数设定值如表1所示。
。模拟采用的参数设定值如表1所示。
图1~图2反映了在Hurst参数为0.75的分数布朗运动环境下CM策略和CPPI策略下的收益保证价值对金融市场参数的敏感性。虽然两种策略中的期初风险性资产占投资资产组合的比例均为0.6,但CPPI策略下所测算的收益保证价值较CM策略下小,这说明CPPI策略下期末不能偿付收益保证的风险较低,进而可被视为一种更安全的策略。原因是因为相对于CM策略而言,CPPI策略的价值底线对资产组合的资产具有缓冲保护的作用。图1中,随着收益保证水平参数的逐渐增大,每期收益保证水平逐渐提高;图2中,随着风险资产的波动率逐渐增大,两策略下期末不能偿付收益保证的风险均不断增大,从而收益保证价值都逐渐增加。此外,图2反映出CM策略下收益保证价值对风险资产波动率更为敏感,这是由于CPPI策略具有缓冲保护机制,所以CPPI策略下收益保证价值的变化较CM下平缓。
Table 1. Simulating parameters
表1. 模拟参数
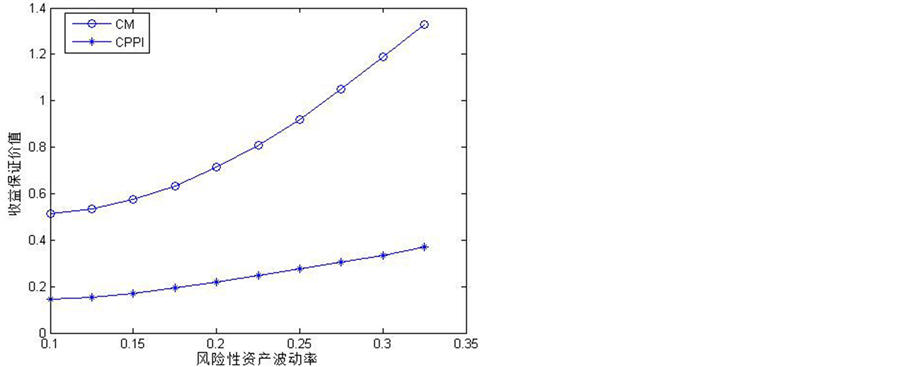
Figure 1. The influence of volatility
图1. 风险性资产波动率的影响
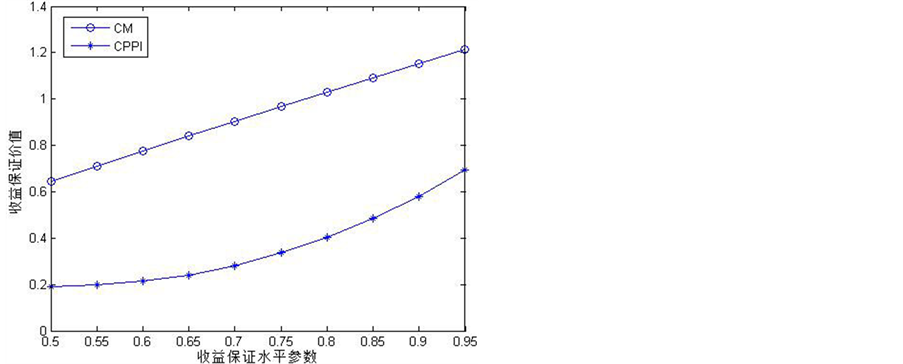
Figure 2. The influence of return guarantees
图2. 收益保证水平参数的影响
图3和图4反映了不同保证期限下,资产配置策略参数对CM策略和CPPI策略下多期收益保证价值的影响。两幅图都表明,随着保证期限的增加,该资产配置策略所蕴含的风险明显增大,从而收益保值价值显著增加,说明了若收益保证型金融产品投资机构转变短期收益保证为长期收益保证性时,必须充分考虑到由于保证期限的变化所引起的收益保证价值的显著变化。图3中,随着资产组合中风险性资产所占比例k的逐渐增大;图4中,随着策略乘数的增大和期初价值底线的降低,即风险性资产占资产组合的比例增大,CM策略和CPPI策略所蕴含的期末不能偿付收益保证价值的风险越来越大,即两策略的安全性越来越差,从而CM策略下和CPPI策略下的多期收益保证价值逐渐增加,因此使得相对应的受益保证价值曲线或曲面均是逐渐向上,并且越来越陡峭。

Figure 3. The influence of parameter in CM strategy
图3. CM策略参数的影响

Figure 4. The influence of parameters in CPPI strategy
图4. CPPI策略参数的影响
致谢
感谢闫理坦教授在本论文的研究工作中对我的悉心指导,谨在此向闫老师致以最诚挚的感谢和最崇高的敬意!
基金项目
国家自然科学基金资助课题(No. 11571071)。
文章引用
邓艳莲,陆允生. 分数布朗运动环境下的资产配置策略多期收益保证价值的测算
Pricing Multi-Period Return Guarantees Combined with Asset Allocation Strategy under Fractional Brownian Motion[J]. 金融, 2016, 06(02): 64-73. http://dx.doi.org/10.12677/FIN.2016.62007
参考文献 (References)
- 1. Brennan, J.M. and Schwartz, E.S. (1976) The Pricing of Equity-Linked Life Insurance Policies with an Asset Value Guarantee. Journal of Financial Economics, 3, 195-213. http://dx.doi.org/10.1016/0304-405X(76)90003-9
- 2. 张飞, 刘海龙. 价格跳跃风险下CPPI策略多期收益保证价值的测算[J]. 系统工程理论与实践, 2014, 34(8): 1944- 1951.
- 3. 王亦奇, 刘海龙. 结合资产配置策略测算多期收益保证价值[J]. 管理科学学报, 2011, 14(11): 42-51.
- 4. Black, F. and Scholes, M. (1973) The Pricing of Options and Gorporate Liabilities. Journal of Political Economy, 81, 637-654. http://dx.doi.org/10.1086/260062
- 5. Shiryaev, A.N. (1999) Essentials of Stochastic Finance. World Scientific, Singapore.
- 6. Rogers, L. (1997) Arbitrage with Fractional Brownian Motion. Mathematical Finance, 7, 95-105. http://dx.doi.org/10.1111/1467-9965.00025
- 7. Bjork, T. and Hult, H. (2005) A Note on Wick Products and the Fractional Black-Scholes Model. Finance and Stochastics, 9, 197-209. http://dx.doi.org/10.1007/s00780-004-0144-5
- 8. Sottinen, T. (2001) Fractional Brownian Motion, Random Walks and Binary Market Models. Finance and Stochastics, 5, 343-355. http://dx.doi.org/10.1007/PL00013536
- 9. Necula, C. (2002) Option Pricing in a Fractional Brownian Motion Environment. Work Papers. http://dx.doi.org/10.2139/ssrn.1286833
- 10. Hu, Y. and Oksendal, B. (2003) Fractional White Noise Calculus and Applications to Finance. Infinite Dimensional Analysis, Quantum Probability and Related Topics, 6, 1-32. http://dx.doi.org/10.1142/S0219025703001110
- 11. Biagini, F. and Hu, Y., Øksendal, B. and Zhang, T. (2008) Stochastic Calculus for Fractional Brownian Motion and Applications. Springer, Berlin.
- 12. Rostek, S. and Schobel, R. (2006) Risk Preference Based Option Pricing in a Fractional Brownian Market. Tubinger Diskussinsbeitrag, Tu-ebingen.
