Pure Mathematics
Vol.05 No.01(2015), Article ID:14673,5
pages
10.12677/PM.2015.51002
The Invertible Linear Operator Preserving {1,2}-Inverses of Matrices over Semirings
Linhong Zhang
Xi’an No. 3 Middle School, Xi’an
Email: jiayoulinhong@163.com
Received: Nov. 7th, 2014; revised: Dec. 2nd, 2014; accepted: Dec. 20th, 2014
Copyright © 2015 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Linear preserve problem has been a relatively active topic in the matrix theory research. In the paper, we mainly study invertible linear operators that preserve {1,2}-inverses of matrices over semirings. It is completely characterized that invertible linear operators which preserve {1,2}- inverse of matrices over chain semiring, the nonnegative integers, and the nonnegative reals.
Keywords:Semiring, {1,2}-Inverse, Invertible Linear Operator
保持半环上矩阵{1,2}-逆的可逆线性算子
张林红
西安市第三中学,西安
Email: jiayoulinhong@163.com
收稿日期:2014年11月7日;修回日期:2014年12月2日;录用日期:2014年12月20日

摘 要
线性保持问题一直是矩阵论研究中一个较为活跃的课题。本文主要研究了保持半环上矩阵{1,2}-逆的可逆线性算子。完全的刻画了保持链半环、非负整数环和非负实数环上的矩阵{1,2}-逆的可逆算子。
关键词 :半环,{1,2}-逆,可逆线性算子

1. 引言
研究各种不变量以及保持不变量的映射和变换历来是数学各学科领域关注的问题。刻画矩阵空间的保持不变量的线性映射已经成为矩阵论研究中一个极为活跃的课题,通常被称为“线性保持问题”。线性保持问题是保持问题中最基本、最常见的保持问题,一方面是由于它的理论价值;另一方面是由于它在微分方程、系统控制等领域都有着广泛的应用。如在解答微分方程时,为了简化问题,我们希望在解方程组之前对其做一变换,一般要求变换应该是简单的且具有较好的性质,这些都与线性保持问题有关。
许多学者已经研究了保持半环上矩阵不变量的线性算子。Song,Kang和Beasley [1] ,Dolzan和Oblak [2] ,以及Olrel [3] 研究了保持幂等阵的线性算子。Song,Kang和Jun [4] ,以及Li和Tan [5] 研究了保持幂零阵的线性算子。Song,Kang,Jun,Beasley和Sze在文献[2] [5] [6] 中研究了保持正则性的线性算子。Pshenitsyna [7] 研究了保持可逆矩阵的线性算子。
2. 准备知识
半环的定义一般有多种,下面给出一种定义。
定义2.1 设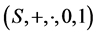 是一个
是一个 -型代数,其中
-型代数,其中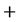 和
和 是二元运算,
是二元运算, 和
和 是零元运算。若
是零元运算。若 满足下列条件:
满足下列条件:
1) 是一个可换含幺半群;
是一个可换含幺半群;
2)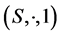 是一个含幺半群;
是一个含幺半群;
3) ;
;
4)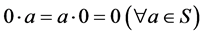 ;
;
5) 。
。
则称 是半环。
是半环。
设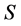 是半环,
是半环, 表示
表示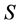 上
上 阶矩阵的全体。
阶矩阵的全体。 表示
表示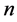 阶单位矩阵,且
阶单位矩阵,且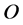 是
是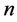 阶零矩阵。定义
阶零矩阵。定义 上的
上的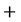 和
和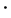 如下:
如下:

容易验证,在上述定义的运算下, 是半环。
是半环。
定义2.2 设 是
是 上的一个算子,若满足对任意
上的一个算子,若满足对任意 ,
, 有
有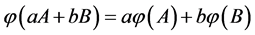 则称
则称 是
是 上的线性算子。
上的线性算子。
设 。如果存在
。如果存在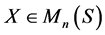 使得
使得 且
且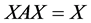 成立,那么称
成立,那么称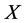 是
是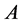 一个的
一个的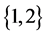 -逆。设
-逆。设 是
是 上的一个线性算子,若对任意
上的一个线性算子,若对任意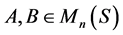 ,
, 是
是 的一个
的一个 -逆蕴涵着
-逆蕴涵着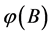 是
是 的一个
的一个 -逆,则称
-逆,则称 是保持矩阵
是保持矩阵 -逆的线性算子。
-逆的线性算子。
定义2.3 设 是半环。若
是半环。若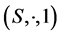 是可换的,则称
是可换的,则称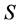 是可换的。若对任意的
是可换的。若对任意的 ,
, 蕴涵着
蕴涵着 ,则称
,则称 是反环。若对任意的
是反环。若对任意的 ,
, 蕴涵着
蕴涵着 或
或 ,则称
,则称 是无零因子的。
是无零因子的。
以下文中 表示正整数的全体,
表示正整数的全体, 表示
表示 ,
,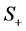 表示
表示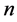 次对称群,
次对称群, 不做特别说明均表示半环。
不做特别说明均表示半环。
设是 有界链,其中
有界链,其中 是最小元,
是最小元,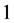 是最大元,且
是最大元,且 。定义
。定义 上的
上的 和
和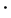 如下:
如下:

则 成为半环,称其为链半环。特别的,如果链半环是闭区间
成为半环,称其为链半环。特别的,如果链半环是闭区间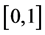 ,那么称
,那么称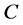 为模糊半环。易见,链半环一定是可换无零因子反环。
为模糊半环。易见,链半环一定是可换无零因子反环。
设 是实数环
是实数环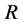 (在普通的加法和乘法下)的含幺子环,的非负部分记为
(在普通的加法和乘法下)的含幺子环,的非负部分记为 。容易验证,
。容易验证,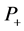 是半环。非负整数半环
是半环。非负整数半环 和非负实数半环
和非负实数半环 都是
都是 的例子。显然,
的例子。显然,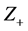 和
和 是可换无零因子反环。
是可换无零因子反环。
设 。
。 表示
表示 的转置。定义
的转置。定义 ,乘方定义如下:
,乘方定义如下:
 。
。
定义2.4 对于矩阵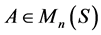 ,若存在
,若存在 使得
使得 ,则称
,则称 是可逆矩阵。
是可逆矩阵。
定义2.5 对于矩阵 ,如果的每一行和每一列都有一个非零元,且非零元是
,如果的每一行和每一列都有一个非零元,且非零元是 ,那么称
,那么称 是一个排列矩阵。
是一个排列矩阵。
若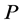 是排列矩阵,则
是排列矩阵,则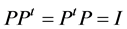 。文献[6] 也证明了
。文献[6] 也证明了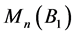 中排列矩阵是仅有的可逆矩阵。
中排列矩阵是仅有的可逆矩阵。
定义2.6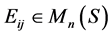 表示在
表示在 位置为
位置为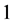 ,其余位置为
,其余位置为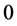 的矩阵,我们称这样的
的矩阵,我们称这样的 是原子(见文献[1] [4] [6] )。
是原子(见文献[1] [4] [6] )。
记 ,对任意的
,对任意的 ,容易得出
,容易得出

3. 主要结果及证明
引理3.1 设 是可换反环,
是可换反环,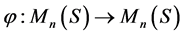 是线性算子。则
是线性算子。则 是可逆的充分必要条件是存在
是可逆的充分必要条件是存在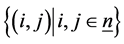 上的排列
上的排列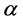 和可逆元
和可逆元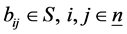 ,使得
,使得 。
。
引理及其证明见于文献[1] 。
下文中,
定理3.2 设 是可换无零因子反环,
是可换无零因子反环,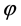 是
是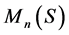 上的线性算子。若
上的线性算子。若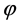 是保持矩阵
是保持矩阵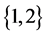 -的可逆线性算子,则存在
-的可逆线性算子,则存在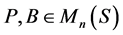 使得
使得
 或
或
其中 是排列矩阵,
是排列矩阵,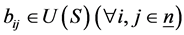 ,且
,且 。
。
证明:由于 可逆的,根据引理3.1,则存在
可逆的,根据引理3.1,则存在 上的排列
上的排列 和
和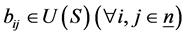 ,使得
,使得 。
。
对于任意的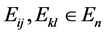 ,容易证得
,容易证得
 (1)
(1)
即对于任意的 ,则
,则 的
的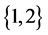 -逆为其转置
-逆为其转置 。
。
从而存在 ,使得对于任意的
,使得对于任意的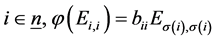 。否则,若
。否则,若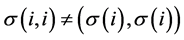 即
即 且
且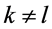 ,
,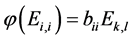 。由于
。由于 是保持
是保持 -逆的,
-逆的,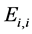 的
的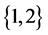 -逆就是
-逆就是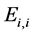 ,则
,则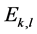 的逆也为
的逆也为 ,且
,且 。这明显与(1)矛盾。
。这明显与(1)矛盾。
又由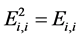 可推出
可推出 。
。
在 中取
中取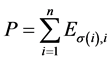 ,定义
,定义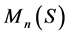 上的线性算子
上的线性算子 如下:
如下:
 。
。
不难看出 仍是保持矩阵
仍是保持矩阵 -逆的可逆线性算子。
-逆的可逆线性算子。
对于任意的 。
。
对于任意的 ,设
,设 。由引理3.1可知
。由引理3.1可知 。假设
。假设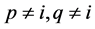 。由
。由 ,可知
,可知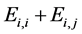 的
的 -逆就是其本身
-逆就是其本身 ,又因为
,又因为 是保持
是保持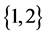 -逆的,所
-逆的,所
以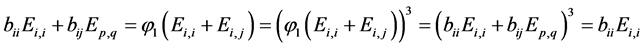 矛盾。从而有
矛盾。从而有 或
或 。类似的,有
。类似的,有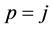 或
或 。进一步,则有
。进一步,则有 或
或 。
。
对于 ,当
,当 时,结论显然成立。
时,结论显然成立。
下面证明 的情形。
的情形。
对于某个 ,设
,设 。假设存在
。假设存在 使得
使得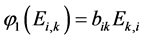 。则由
。则由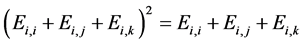 ,可知
,可知 的
的 -逆就是其本身
-逆就是其本身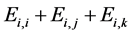 ,又因为
,又因为 是
是
保持 -逆的,所以
-逆的,所以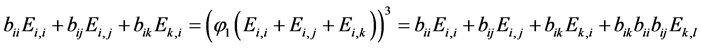 矛盾。
矛盾。
从而对任意的 。进一步,
。进一步,
 。
。
故 。
。
类似的,若对某个 ,
, ,则存在
,则存在 使得
使得 。
。
综上,结论已证毕。
4. 推论及应用
4.1. 推论1及应用
推论4.1.1 设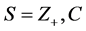 ,
, 是
是 上的线性算子。则
上的线性算子。则 是保持矩阵
是保持矩阵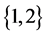 -逆的可逆线性算子的充分必要条件是存在排列矩阵
-逆的可逆线性算子的充分必要条件是存在排列矩阵 ,使得
,使得
 或
或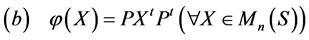 。
。
证明:必要性:由已知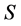 是可换无零因子反环,且由已知
是可换无零因子反环,且由已知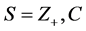 ,则
,则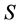 中的可逆元只有1。由定理3.2可得存在排列矩阵
中的可逆元只有1。由定理3.2可得存在排列矩阵 ,使得
,使得 是下列形式之一:
是下列形式之一: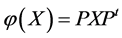 或
或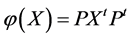 。
。
充分性:当 时,容易验证,
时,容易验证, 是可逆的。对于任意的
是可逆的。对于任意的 ,若有
,若有 ,则
,则
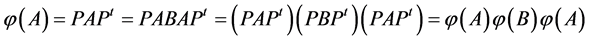 ;
;
 。
。
故 是保持
是保持 -逆的。
-逆的。
类似的可以证明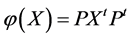 的情形。
的情形。
综上,结论已证毕。
例4.1.2 设 是
是 中的矩阵。定义
中的矩阵。定义 上的一个线性算子
上的一个线性算子 如下:
如下:
 。
。
不难验证, 是保持矩阵
是保持矩阵 -的可逆线性算子。
-的可逆线性算子。
例4.1.3 设 是
是 中的矩阵。定义
中的矩阵。定义 上的一个线性算子
上的一个线性算子 如下:
如下:
 。
。
不难验证, 是保持矩阵
是保持矩阵 -的可逆线性算子。
-的可逆线性算子。
4.2. 推论2及应用
推论4.2.1 设 是
是 上的线性算子。则
上的线性算子。则 是保持矩阵
是保持矩阵 -的可逆线性算子的充分必要条件是存在可逆矩阵
-的可逆线性算子的充分必要条件是存在可逆矩阵 ,使得
,使得

或
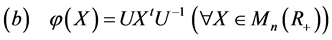 。
。
证明:必要性:由定理3.2知,当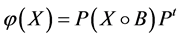 时,对于任意的
时,对于任意的 ,存在
,存在 使得
使得 ,且
,且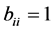 。对于任意的
。对于任意的 ,由
,由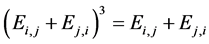 知
知
 。
。
进一步,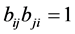 。当
。当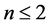 时,容易得出结论是成立的。
时,容易得出结论是成立的。
下面讨论 的情形。对于互不相等的
的情形。对于互不相等的 ,由
,由 知
知

进一步,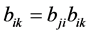 。结合
。结合 和
和 可推出对任意的
可推出对任意的 ,有
,有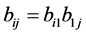 。从而有
。从而有
 ,
,
其中 。设
。设 ,
, 是可逆的。故
是可逆的。故 。
。
类似可证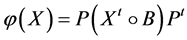 的情形。
的情形。
充分性:当 时,容易验证,
时,容易验证, 是可逆的。对于任意的
是可逆的。对于任意的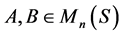 ,若有
,若有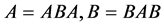 ,则
,则
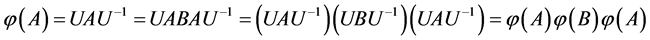 ;
;
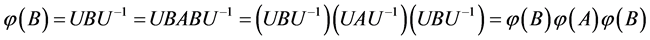 。
。
故 是保持
是保持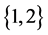 -逆的。
-逆的。
类似的可以证明 的情形。
的情形。
综上,结论已证毕。
例4.2.2 设 是中
是中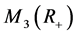 的矩阵。定义
的矩阵。定义 上的一个线性算子
上的一个线性算子 如下:
如下:
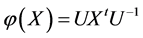 。
。
不难验证,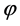 是保持矩阵
是保持矩阵 -的可逆线性算子。
-的可逆线性算子。
文章引用
张林红, (2015) 保持半环上矩阵{1,2}-逆的可逆线性算子
The Invertible Linear Operator Preserving {1,2}-Inverses of Matrices over Semirings. 理论数学,01,8-13. doi: 10.12677/PM.2015.51002
参考文献 (References)
- 1. Song, S.Z., Kang, K.T. and Beasley, L.B. (2007) Idempotent matrix preservers over Boolean algebras. Journal of the Korean Mathematical Society, 44, 169-178.
- 2. Dolzan, D. and Oblak, P. (2009) Idempotent matrices over antirings. Linear Algebra and Its Applications, 431, 823- 832.
- 3. Orel, M. (2010) Nonbijective idempotents preservers over semirings. Journal of the Korean Mathematical Society, 47, 805-818.
- 4. Song, S.Z., Kang, K.T. and Jun, Y.B. (2006) Linear preservers of Boolean nilpotent matrices. Journal of the Korean Mathematical Society, 43, 539-552.
- 5. Li, H.H. and Tan, Y.J. (2007) Linear operators that strongly preserve nilpotent matrices over antinegative semirings. Northeastern Mathematical Journal, 23, 71-86.
- 6. Song, S.Z., Kang, K.T., Beasley, L.B. and Sze, N.S. (2008) Regular matrices and their strong preservers over semirings. Linear Algebra and Its Applications, 429, 209-223.
- 7. Pshenitsyna, O.A. (2009) Maps preserving invertibility of matrices over semirings. Russian Mathematical Surveys, 64, 162-164.