Pure Mathematics
Vol.05 No.02(2015), Article ID:14897,5
pages
10.12677/PM.2015.52005
Moderate Deviations of Hypothesis Testing in Stochastic Partial Differential Equations
Ruwei Cui
Nanjing University of Aeronautics and Astronautics, Nanjing Jiangsu
Email: cuiruwei@126.com
Received: Feb. 12th, 2015; accepted: Feb. 25th, 2015; published: Mar. 2nd, 2015
Copyright © 2015 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we focus our attention on the hypothesis testing problem for the drift coefficient in the diagonalizable stochastic evolution equation driven by additive fractional Brownian motion with Hurst parameter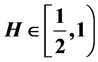 . And when the dimension N is fixed and observation time T tends to infinity, with the help of moderate deviations for the log-likelihood ratio process, we give the negative regions and obtain the decay rates of the error probabilities. Moreover, we also apply our results to some examples.
. And when the dimension N is fixed and observation time T tends to infinity, with the help of moderate deviations for the log-likelihood ratio process, we give the negative regions and obtain the decay rates of the error probabilities. Moreover, we also apply our results to some examples.
Keywords:Fractional Brownian Motion, Stochastic Partial Differential Equation, Hypothesis Testing, Moderate Deviation

抛物型SPDE中假设检验的中偏差原理
崔汝伟
南京航空航天大学,江苏 南京
Email: cuiruwei@126.com
收稿日期:2015年2月12日;录用日期:2015年2月25日;发布日期:2015年3月2日

摘 要
本论文的目的是研究由可加分布朗运动驱动的随机偏微分方程中漂移系数的假设检验问题,其中Hurst系数为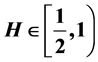 。并且我们利用对数似然比的中偏差原理,在维数N固定,时间T趋于无穷的情况下,给出了未知参数的拒绝域和两类错误的衰减速度。最后我们将结果应用在几个例子当中。
。并且我们利用对数似然比的中偏差原理,在维数N固定,时间T趋于无穷的情况下,给出了未知参数的拒绝域和两类错误的衰减速度。最后我们将结果应用在几个例子当中。
关键词 :可加分数布朗运动,随机微分方程,假设检验,中偏差

1. 介绍
本文我们讨论下面由可加分数布朗运动驱动的抛物型随机偏微分方程:
假设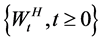 是一个定义在Hilbert空间
是一个定义在Hilbert空间 上的柱状分数布朗运动,即
上的柱状分数布朗运动,即 ,其中
,其中
 是带有相同Hurst参数
是带有相同Hurst参数 的独立分数布朗运动,且
的独立分数布朗运动,且 为
为 的一组标准正交
的一组标准正交
基。有以下由可加分数布朗运动驱动的随机偏微分方程:
 (1)
(1)
这里 是
是 上的线性算子,
上的线性算子, 是未知的。
是未知的。
本文我们假设(1)为可对角化及抛物型的。Cialenco,Lototsky和Pospisil [1] 证明了解的存在性和唯一性, 并且引入了参数 的极大似然估计量:
的极大似然估计量:

Demo [2] 给出了鞅的中偏差原理。若方程为可对角化的抛物型方程,Cialenco,Lototsky和Pospisil [1] 给出了参数估计量的大数定律和中心极限定理。同时Hu和Nualart [3] 通过研究对数似然率的大偏差原理,分别在时间和维数趋于无穷的时候构造了相应的假设检验拒绝域。
本文中令 是方程(2.1)的解关于
是方程(2.1)的解关于 的傅里叶系数, 其中
的傅里叶系数, 其中 满足如下一维分数O-U过程
满足如下一维分数O-U过程

对于 ,令
,令 是
是 到
到 的投影。令
的投影。令 ,则
,则 。这里令
。这里令 是
是 在
在 上的分布。因为
上的分布。因为 是相互独立,所以
是相互独立,所以 ,从而对数似然比函数为:
,从而对数似然比函数为:
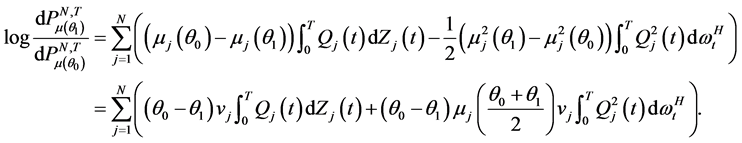
在维数N固定,时间 时,我们考虑漂移系数
时,我们考虑漂移系数 的假设检验的问题:
的假设检验的问题:

由Neyman-Pearson引理,可以得到上述假设检验问题的拒绝域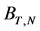 有这样的形式
有这样的形式 ,
,
其中参数c待定。当接受 但
但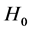 是正确的时候,概率
是正确的时候,概率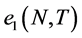 是第一类错误概率。当接受
是第一类错误概率。当接受 但
但 是正确的时候,
是正确的时候, 是第二类错误概率,i.e.
是第二类错误概率,i.e.
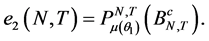

为了确定否定域中的参数c,我们首先来探讨对数似然比函数的大偏差原理。然后利用其,我们可以确定拒绝域的参数,最后我们可以得出两类错误 和
和 的衰减速度。
的衰减速度。
定理1 令 是一个大于零的函数并且满足
是一个大于零的函数并且满足
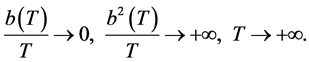
对于任意的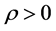 ,令
,令

则由
 (2)
(2)
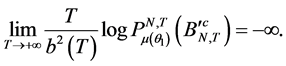 (3)
(3)
2. 定理的证明
现在我们先讨论一下对数似然比过程 的中偏差原理。令
的中偏差原理。令 是对数似然比过程
是对数似然比过程 在
在 下的对数矩生成函数,即
下的对数矩生成函数,即
 (4)
(4)
为了证明定理内容,我们引入下面引理
引理2.1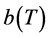 如定理1中定义。则在
如定理1中定义。则在 概率下
概率下

满足大偏差定理,并且速度为 ,速率函数为
,速率函数为
证明 定义

由定理1中定义,对于所有的 ,存在足够大的T使
,存在足够大的T使

令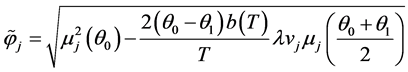 ,根据Girsanov公式我们可以看出
,根据Girsanov公式我们可以看出

这里 。那么我们由Kleptsyna,Le Breton和Roubaud [4] 中的命题3.2可以得出
。那么我们由Kleptsyna,Le Breton和Roubaud [4] 中的命题3.2可以得出

其中
 (5)
(5)
从而我们可以得到

其中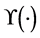 如(5)定义,并对于所有的
如(5)定义,并对于所有的 有
有
通过简单化简计算,可以得到
 (6)
(6)
而且

所以由上我们可以得到
 (7)
(7)
结合(6)和(7),我们可以得到

综上并根据Gartner-Ellis定理即可以得到引理结论。
结合引理2.1和式子 ,我们可以得到如下结论。
,我们可以得到如下结论。
推论2.1 如定理1中定义。则在
如定理1中定义。则在 概率下,
概率下, 满足大偏差定理,并且速度为
满足大偏差定理,并且速度为 ,速率函数为
,速率函数为
定理1的证明 (2)是引理2.1的直接结论。令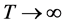 ,我们可以得到
,我们可以得到

其次(3)可以由推论2.1直接得到。
3. 应用
令G是 中一个有界光滑区域,且
中一个有界光滑区域,且 。
。 是G上的带有零边界条件的拉普拉斯算子。通过Safarov和Vassiliev [5] 可知,
是G上的带有零边界条件的拉普拉斯算子。通过Safarov和Vassiliev [5] 可知, 的特征向量构成了
的特征向量构成了 中的完备正交基。
中的完备正交基。
我们来看如下的几个例子[6] [7] 。
1) 考虑如下方程:

其中 且
且

我们可以看到
 (8)
(8)
由定理1,我们可以得到如下结论
命题3.1 令 是一个正数序列并且满足下列条件
是一个正数序列并且满足下列条件

则有

2) 考虑如下方程:

其中 ,
,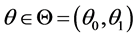 ,且
,且

令 是拉普拉斯算子
是拉普拉斯算子 的特征值,则
的特征值,则

因为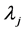 皆为负的且存在一个正的常数
皆为负的且存在一个正的常数 使得
使得

故存在 ,对于任意的
,对于任意的 ,当
,当 时,都有
时,都有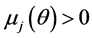 。由定理1,我们可以得到如下结论
。由定理1,我们可以得到如下结论
命题3.2 令 是一个正数序列并且满足下列条件
是一个正数序列并且满足下列条件

则有

致谢
本论文是在我的导师的指导下完成的。感谢导师给予我们的支持,感谢南京航空航天大学数学系的各位老师给予我们的指导和帮助,感谢各位文献作者的成果给予我们的借鉴。
文章引用
崔汝伟, (2015) 抛物型SPDE中假设检验的中偏差原理
Moderate Deviations of Hypothesis Testing in Stochastic Partial Differential Equations. 理论数学,02,28-33. doi: 10.12677/PM.2015.52005
参考文献 (References)
- 1. Cialenco, I., Lototsky, S.V. and Pospisil, J. (2009) Asymptotic properties of the maximum likelihood estimator for stochastic parabolic equations with additive fractional Brownian motion. Stochastics and Dynamics, 9, 169-185.
- 2. Demo, A. (1996) Moderate deviations for martingales with bounded jumps. Electronic Communica-tions in Probability, 1, 11-17.
- 3. Hu, Y.Z. and Nualart, D. (2010) Parameter estimation for Ornstein-Uhlenbeck processes. Statistics Probability Letters, 80, 1030-1038.
- 4. Kleptsyna, M.L., Le Breton, A. and Roubaud, M.C. (2002) Statistical analysis of the fractional Ornstein-Uhlenbeck type process. Statistical Inference for Stochastic Processes, 5, 229-248.
- 5. Safarov, Y. and Vassiliev, D. (1997) The asymptotic distribution of eigenvalues of partial differential operators. Translations of Mathematical Monographs, 155.
- 6. Prakasa Rao, B.L.S. (2004) Parameter estimations for some stochastic partial differential equations driven by infinite dimensional fractional Brownian motion. Theory of Stochastic Process, 10, 116-125.
- 7. Bercu, B. and Rouault, A. (2002) Sharp large deviations for the Ornstein-Uhlenbeck process. Theory of Probability and Its Applications, 46, 1-19.