Pure Mathematics
Vol.07 No.03(2017), Article ID:20483,8
pages
10.12677/PM.2017.73017
Estimates on the Non-Real Eigenvalues of Fourth Order Indefinite Differential Operators
Fan Hu, Jiong Sun, Kun Li, Xiaoling Hao
School of Mathematical Sciences, Inner Mongolia University, Hohhot Inner Mongolia

Received: Apr. 21st, 2017; accepted: May 6th, 2017; published: May 10th, 2017

ABSTRACT
The present paper gives an estimate on the non-real eigenvalues for a class of fourth order differential operators. Using operator theory and classical analysis, we study the eigenvalue problem for indefinite differential operators produced by the signs of weight function, and discuss the cases of many turning points and a turning point for the weight function respectively, then we get the estimate on the real and imaginary parts of the non-real eigenvalues.
Keywords:Fourth Order Differential Operators, Non-Real Eigenvalue, Indefinite Weight Function
四阶不定微分算子非实特征值的估计
胡帆,孙炯,李昆,郝晓玲
内蒙古大学数学科学学院,内蒙古 呼和浩特
收稿日期:2017年4月21日;录用日期:2017年5月6日;发布日期:2017年5月10日

摘 要
本文研究了一类关于四阶微分算子非实特征值的估计。利用算子理论和经典分析,研究了由权函数变号产生的不定微分算子的特征值问题,对权函数具有多个拐点时和只有一个拐点的情况分别进行了讨论,得到非实特征值实部和虚部的估计。
关键词 :四阶微分算子,非实特征值,不定权函数

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文考虑四阶边值问题
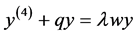 (1)
(1)
边界条件为
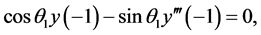 (2)
(2)
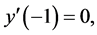 (3)
(3)
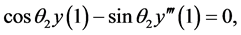 (4)
(4)
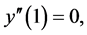 (5)
(5)
其中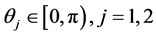 。
。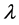 是谱参数,
是谱参数, 都是实值函数,并且
都是实值函数,并且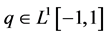 。当
。当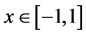 时,
时,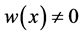 a.e.,且
a.e.,且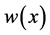 在
在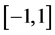 上改变符号。
上改变符号。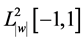 表示所有勒贝格可测函数构成的Hilbert空间,
表示所有勒贝格可测函数构成的Hilbert空间,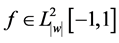 满足
满足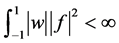 。
。
常微分算子谱理论的广泛研究使得算子谱的内容更加丰富,特别是关于特征值的研究取得了许多成果。自二十世纪以来,研究发现正则不定的Sturm-Liouville问题可能具有非实的特征值,对这类非实特征值实部和虚部的估计至今仍然是一个开放性问题 [1] [2] 。早在二十世纪初,Haupt,Richardson等人就对不定性质的问题进行了讨论 [3] [4] 。近年来一些学者对不定的Sturm-Liouville问题进行了更进一步的研究。其中一些学者最早对Richardson方程 及Dirichlet边界条件
及Dirichlet边界条件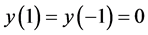 中非实特征值的存在性进行了研究,之后越来越多的作者对这类问题进行了深入广泛的研究 [5] [6] [7] [8] 。对于二阶形式不定的Sturm-Liouville (S-L)问题,只要其相应的右定问题有负的特征值
中非实特征值的存在性进行了研究,之后越来越多的作者对这类问题进行了深入广泛的研究 [5] [6] [7] [8] 。对于二阶形式不定的Sturm-Liouville (S-L)问题,只要其相应的右定问题有负的特征值
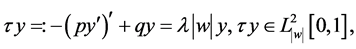
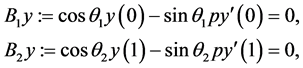
则二阶不定的S-L方程有非实特征值 [9] [10] 。
对于正则不定的Sturm-Liouville问题,2014年Qi和Chen在Dirichlet边界条件以及权函数变号一次或绝对连续的条件下,分离实部和虚部给出了不定问题非实特征值上界的估计 [11] 。2013,Xie和Qi给出在具有一般分离型边界条件以及权函数绝对连续或更弱的条件下,通过分离实部和虚部给出了不定Sturm-Liouville问题非实特征值的上界估计 [12] 。同年,Behrndt, Chen, Philipp和Qi得到了权函数可以无穷次变号的不定Sturm-Liouville问题非实特征值的上界估计 [13] 。
许多研究工作已对二阶不定Sturm-Liouville问题的非实特征值给出了很好的估计。但是由于对函数的导数估计上的一些困难,目前对高阶不定微分算子的研究较少。本文拟研究了一类四阶不定微分算子的非实特征值估计。利用算子理论、经典分析、不等式估计,研究了由权函数变号产生的不定微分算子的特征值问题,对权函数具有多个拐点时和只有一个拐点的情况分别进行了讨论,给出了非实特征值实部和虚部的估计。
2. 正文
基本符号与引理
本文中: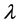 为边值问题(1)-(5)中的非实特征值,
为边值问题(1)-(5)中的非实特征值,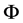 是对应于特征值
是对应于特征值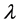 的特征函数,并且这里
的特征函数,并且这里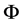 满足
满足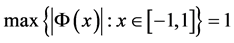 。为了描述定理1和定理2,我们给出如下记号,令
。为了描述定理1和定理2,我们给出如下记号,令
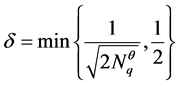
其中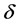 为区间
为区间 的长度,
的长度,
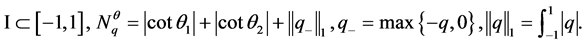
若 ,定义
,定义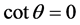 。因为
。因为 a.e.
a.e.
我们可以找到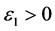 ,使得:
,使得:
 (6)
(6)
引理1. 若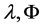 如上定义,且
如上定义,且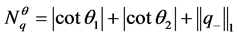 ,则
,则
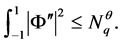 (7)
(7)
证明 在方程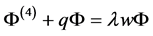 两边同时乘以
两边同时乘以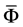 ,并且在
,并且在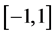 上进行积分得到
上进行积分得到
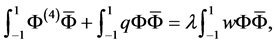
由分部积分得
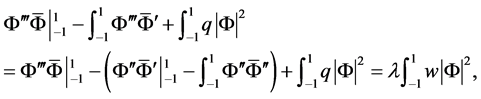
由边界条件(2)-(5) 知
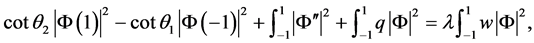
因为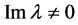 ,由上式可知
,由上式可知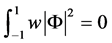 ,因此
,因此
 (8)
(8)
由于 ,所以由(8)式得到
,所以由(8)式得到
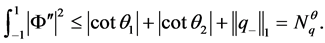
证毕。
引理2. 若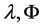 如上定义,且
如上定义,且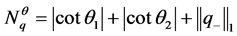 ,则
,则
 (9)
(9)
证明 由边界条件(3)知
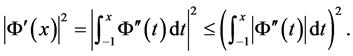
由Cauchy-Schwarz不等式和引理1可得
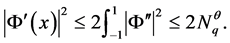
证毕。
引理3. 若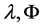 如上定义,且
如上定义,且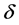 如之前所记,则
如之前所记,则
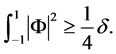 (10)
(10)
证明 假定 ,使得
,使得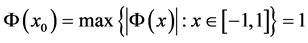 ,则由引理2可知,对
,则由引理2可知,对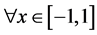 且
且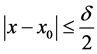 ,有
,有
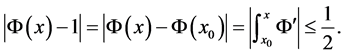
因此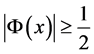 ,
,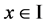 ,其中
,其中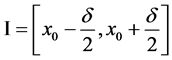 。所以
。所以
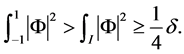
证毕。
3. 结论
3.1. 权函数具有多个拐点时非实特征值的估计
定理1. 若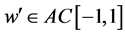 ,
,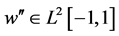 ,
,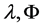 如上定义,则边值问题(1)-(5)的非实特征值
如上定义,则边值问题(1)-(5)的非实特征值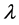 满足
满足
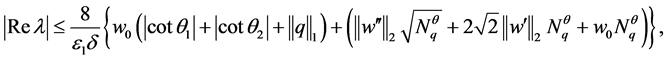 (11)
(11)
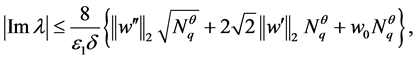 (12)
(12)
其中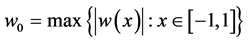 。
。
证明 在方程 两边同时乘以
两边同时乘以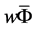 ,并且在
,并且在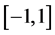 上进行积分得到
上进行积分得到
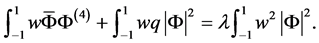
由分部积分得
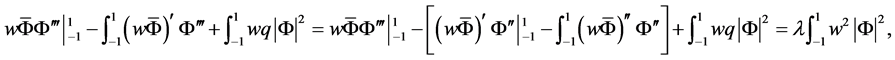
由边界条件(2)-(5)知
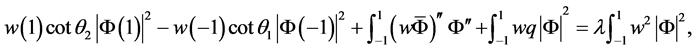
分离实部和虚部得到
 (13)
(13)
 (14)
(14)
由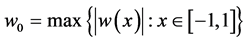 和
和 可得
可得
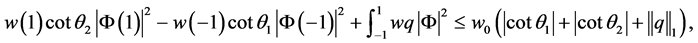 (15)
(15)
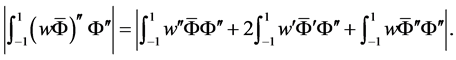
由Cauchy-Schwarz不等式和引理1及引理2知
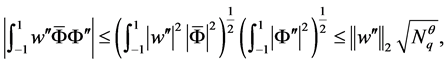

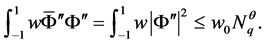
所以由上可得
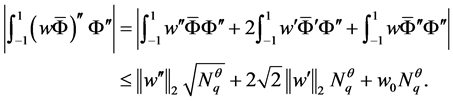 (16)
(16)
由(6)式定义的 及引理3得
及引理3得
 (17)
(17)
综上,由(13)-(17)可得
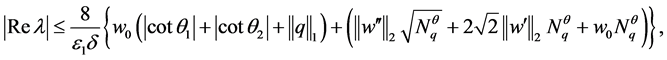
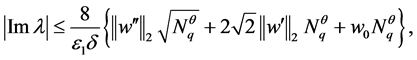
证毕。
3.2. 权函数只有一个拐点时非实特征值的估计
在这部分,我们考虑权函数变号一次时对非实特征值的估计。为此我们假定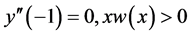 在
在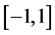 上几乎处处成立,则可以找到
上几乎处处成立,则可以找到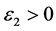 ,使得:
,使得:
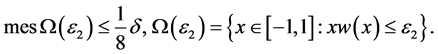 (18)
(18)
定理2. 若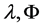 如上定义,
如上定义,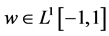 且
且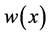 满足(18)式,则边值问题(1)-(5)的非实特征值
满足(18)式,则边值问题(1)-(5)的非实特征值 满足
满足
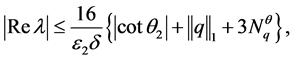 (19)
(19)
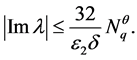 (20)
(20)
证明 在方程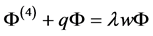 两边同时乘以
两边同时乘以 ,并且在
,并且在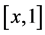 上进行积分得到
上进行积分得到
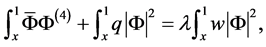
由分部积分得
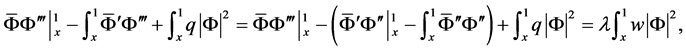
由边界条件(4)和(5)知
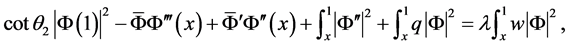
对上式分离实部和虚部得到
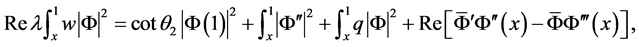 (21)
(21)
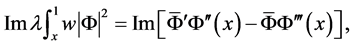 (22)
(22)
在(21)和(22)式中令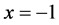 得到
得到
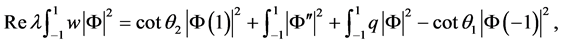
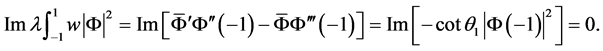
由于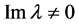 ,所以
,所以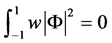 。对(21)式从
。对(21)式从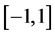 进行积分得
进行积分得
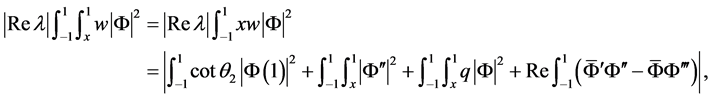 (23)
(23)
由分部积分和边界条件得
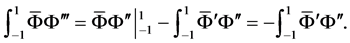
由Cauchy-Schwarz不等式和引理1及引理2知
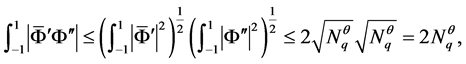
并且由(23)式及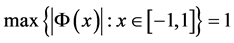 可知
可知
 (24)
(24)
由(18)式定义的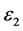 及引理3得
及引理3得
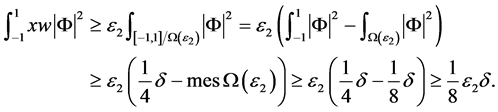 (25)
(25)
同理可得
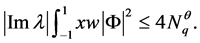
综上,由(21)-(25)可得
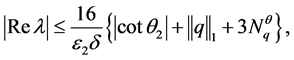
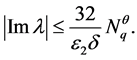
证毕。
资助信息
本文由国家自然科学基金项目(11561050, 11401325)、高等学校博士学科点专项科研基金(新教师类)(20121501120003)支持。
文章引用
胡帆,孙炯,李昆,郝晓玲. 四阶不定微分算子非实特征值的估计
Estimates on the Non-Real Eigenvalues of Fourth Order Indefinite Differential Operators[J]. 理论数学, 2017, 07(03): 141-148. http://dx.doi.org/10.12677/PM.2017.73017
参考文献 (References)
- 1. Mingarelli, A.B. (1986) A Survey of the Regular Weighted Sturm-Liouville Problem—The Non-Definite Case. Mathematics, 109-137.
- 2. Zettl, A. (2005) Sturm-Liouville Theory. American Mathematical Society, Mathematical Surveys and Monographs, 121,
- 3. Haupt, O. (1915) Über eine Methode zum Beweis von oszillations Theoremen. Mathematische Annalen, 76, 67-104. https://doi.org/10.1007/BF01458673
- 4. Richardson, R.G.D. (1912) Theorems of Oscillation for Two Linear Differential Equations of Second Order with Two Parameters. Transactions of the American Mathematical Society, 13, 22-34. https://doi.org/10.1090/S0002-9947-1912-1500902-8
- 5. Atkinson, F.V. and Jabon, D. (1988) Indefinite Sturm-Liouville Problems. Kaper, H.G., Kwong, M.K. and Zettl, A., Eds., Proceedings of the Focused Research Program on Spectral Theory and Boundary Value Problems, Argonne National Laboratory, Lemont, 31-45.
- 6. Binding, P. and Volkmer, H. (1996) Eigencurves for Two-Parameter Sturm-Liouville Equations. SIAM Review, 38, 27-48. https://doi.org/10.1137/1038002
- 7. Fleckinger, J. and Mingarelli, A.B. (1984) On the Eigenvalues of Non-Definite Elliptic Operators. North-Holland Mathematics Studies, 92, 219-227. https://doi.org/10.1016/S0304-0208(08)73696-X
- 8. Turyn, L. (1980) Sturm-Liouville Problems with Several Parameters. Journal Differential Equations, 38, 239-259. https://doi.org/10.1016/0022-0396(80)90007-8
- 9. Curgus, B. and Langer, H. (1989) A Krein Space Approach to Symmetric Ordinary Differential Operators with an Indefinite Weight Functions. Journal Differential Equations, 79, 31-61. https://doi.org/10.1016/0022-0396(89)90112-5
- 10. Mingarelli, A.B. (1982) Indefinite Sturm-Liouville Problems. Lecture Notes in Mathematics, 964, 519-528. https://doi.org/10.1007/BFb0065022
- 11. Qi, J.G. and Chen, S.Z. (2014) A Priori Bounds and Existence of Non-Real Eigenvalues of Indefinite Sturm-Liouville Problems. Journal of Spectral Theory, 4, 53-63. https://doi.org/10.4171/JST/61
- 12. Xie, B. and Qi, J.G. (2013) Non-Real Eigenvalues of Indefinite Sturm-Liouville Problems. Journal Differential Equations, 255, 2291-2301. https://doi.org/10.1016/j.jde.2013.06.013
- 13. Behrndt, J., Chen, S.Z., Philipp, F. and Qi, J.G. (2013) Estimates on the Non-Real Eigenvalues of Regular Indefinite Sturm-Liouville Problems. Proceedings of the Royal Society of Edinburgh, 144, 1113-1126. https://doi.org/10.1017/S0308210513001212