Pure Mathematics
Vol.07 No.05(2017), Article ID:21748,5
pages
10.12677/PM.2017.75047
Two Theorems of Steiner Symmetrization on Convex Bodies
Liying Sun
School of Mathematics and Information Science, Shaanxi Normal University, Xi’an Shaanxi

Received: Aug. 1st, 2017; accepted: Aug. 16th, 2017; published: Aug. 21st, 2017

ABSTRACT
In this paper, we mainly study sufficient conditions for Steiner symmetrization on convex bodies. Firstly, according to the properties of Steiner symmetrization, such as volume-preserving, convexity-preserving, monotonicity, surface area reduction and so on, we constructed a transformation  on convex bodies. Secondly, in accordance to Steiner symmetrization’s characterization and concept, we proved that
on convex bodies. Secondly, in accordance to Steiner symmetrization’s characterization and concept, we proved that  is Steiner symmetrization and came up with two homologous corollaries. Finally, we obtained two sufficient conditions for Steiner symmetrization.
is Steiner symmetrization and came up with two homologous corollaries. Finally, we obtained two sufficient conditions for Steiner symmetrization.
Keywords:Convex Body, Steiner Symmetrization, Minkowski Symmetrization, Hyperplane

凸体的Steiner对称化的两个定理
孙丽英
陕西师范大学,数学与信息科学学院,陕西 西安

收稿日期:2017年8月1日;录用日期:2017年8月16日;发布日期:2017年8月21日

摘 要
本文研究Steiner对称化在凸体上的充分条件。首先,我们根据Steiner对称化的性质,例如:保体积、保凸性、单调性、表面积减小等,构造一个凸体的变换 。其次,我们依据
。其次,我们依据 满足的条件及Steiner对称化的概念,证明出
满足的条件及Steiner对称化的概念,证明出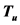 为凸体上的Steiner对称化,并且得到两个类似的推论。本文最后构造出了Steiner对称化的两个充分条件。
为凸体上的Steiner对称化,并且得到两个类似的推论。本文最后构造出了Steiner对称化的两个充分条件。
关键词 :凸体,Steiner对称化,Minkowski对称,超平面

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
1836年,Jakob Steiner介绍了凸体Steiner对称化的过程,并利用Steiner对称化尝试着证明了经典的等周不等式和经典的Brunn-Minkowski不等式,这在 [1] 中第九章有详细证明过程。凸体在做Steiner对称化后,它还有些重要的性质,例如:体积不变、保凸性、单调性、直径不增等,这些性质在 [2] [3] [4] [5] [6] 中可以查看,以及一般的紧集也可以做Steiner对称化,这可以在 [7] 中查看。除了在几何方向有着重要作用外,Steiner对称化还在分析及PDE方向起着重要的作用。
我们要研究的问题是Steiner对称化的反问题,即构造一个在凸体上的变换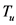 ,它在满足哪些条件的情况下,使之成为Steiner对称?事实上这个问题的答案是肯定的,我们得到了两个定理,在
,它在满足哪些条件的情况下,使之成为Steiner对称?事实上这个问题的答案是肯定的,我们得到了两个定理,在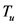 满足保体积、单调性等条件时,确定可以证明出其为Steiner对称化。在 [8] 中讨论了Steiner对称,Minkowski对称,中心对称等,其中就研究了Steiner对称化的反问题,也得出了Steiner对称化的两个漂亮的定理。本文通过构造与其不同的条件,简洁地得出Steiner对称化反问题的两个定理。
满足保体积、单调性等条件时,确定可以证明出其为Steiner对称化。在 [8] 中讨论了Steiner对称,Minkowski对称,中心对称等,其中就研究了Steiner对称化的反问题,也得出了Steiner对称化的两个漂亮的定理。本文通过构造与其不同的条件,简洁地得出Steiner对称化反问题的两个定理。
上述出现的相关概念与记号,将在后文中做详细叙述。
2. 预备知识
设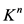 为
为 上全体凸体(紧凸集)构成的集合,
上全体凸体(紧凸集)构成的集合, 表示单位球面,令
表示单位球面,令 为欧几里德范数为1的向量,即
为欧几里德范数为1的向量,即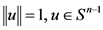 ,且令
,且令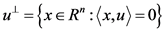 是以
是以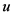 为法向且过原点的超平面,这里
为法向且过原点的超平面,这里 为
为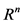 中通常的内积。我们用
中通常的内积。我们用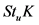 表示
表示 关于法向量
关于法向量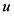 的Steiner对称,以下是它的定义 [5] :
的Steiner对称,以下是它的定义 [5] :

其中,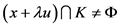 且
且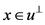 ,这里
,这里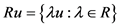 ,
,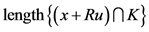 表示线段
表示线段 的长度。
的长度。
注意:由Steiner对称的定义可容易得出:
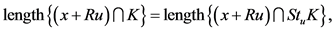
且集合 关于
关于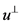 对称。
对称。
下面我们列出一些Steiner对称的性质定理,这将会在后文证明中用到。
命题2.1 [1]  。
。
命题2.2 [1]  ,
,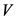 表示体积。
表示体积。
命题2.3 [1] 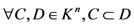 ,则
,则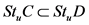 。
。
命题2.4 [1] 若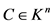 ,则
,则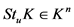 。
。
命题2.5 [5] 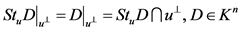 。
。
命题2.6 [9] 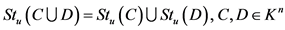 ,且
,且 ,
,
这里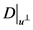 表示
表示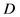 在
在 上的正交投影。
上的正交投影。
说明:这里 非必要条件,但在后文中只需要
非必要条件,但在后文中只需要 即可,其他情况将不作讨论。
即可,其他情况将不作讨论。
Minkowski对称有些好的性质,它与Steiner对称化有一些好的关系 [5] [10] 。
设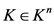 关于法向量
关于法向量 的Minkowski对称为
的Minkowski对称为 ,它的定义如下:
,它的定义如下:
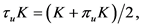
其中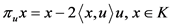 ,即
,即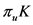 为
为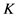 关于
关于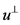 的反射,也就是作
的反射,也就是作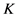 关于
关于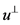 的对称变换。那么当
的对称变换。那么当 关于
关于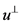 对称时,有
对称时,有 ,我们也很容易得到
,我们也很容易得到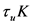 为一个线性算子,即:
为一个线性算子,即:
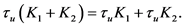
引理2.7 [5]  ,有
,有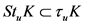 。
。
证明设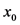 为
为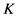 在
在 上的正交投影上的一个点,即
上的正交投影上的一个点,即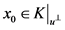 。令
。令 ,则:
,则:
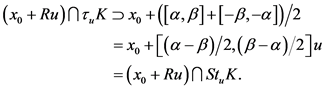
故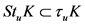 。
。
3. 定理的证明
定理 3.1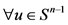 ,
, 为
为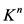 上的映射,
上的映射,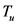 满足以下条件:
满足以下条件:
1)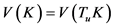 ,
,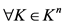 ;
;
2)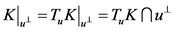 ,
,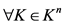 ;
;
3) ,
,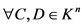 ,
, ;
;
4) 关于
关于 对称,
对称,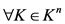 。
。
则 为
为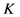 关于法向量
关于法向量 的Steiner对称。
的Steiner对称。
证明
第一步:
设 为垂直于超平面
为垂直于超平面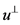 的一条线段,显然
的一条线段,显然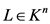 ,则
,则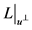 为
为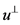 上的一点,记为
上的一点,记为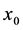 ,即
,即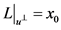 ,由条件(2)可知
,由条件(2)可知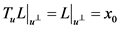 ,且
,且 ,则
,则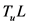 必为垂直于超平面的连续线段,又由条件(1)知
必为垂直于超平面的连续线段,又由条件(1)知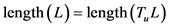 ,最后由条件(4)知
,最后由条件(4)知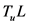 关于
关于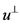 对称,综上所述
对称,综上所述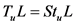 。
。
第二步:
 ,设
,设 ,
, ,则:
,则:
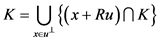 .
.
对于 ,且
,且 时,显然有:
时,显然有:
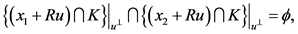
故由(3)可知: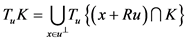 。
。
由第一步可知:

其中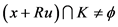 ,
, 。
。
则由上述可得:
 .
.
由第一步和第二步我们可证得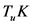 为
为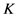 关于法向量
关于法向量 的Steiner对称。证毕。
的Steiner对称。证毕。
推论3.1 ,
, 为
为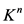 上的映射,
上的映射,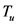 满足以下条件:
满足以下条件:
1)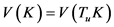 ,
,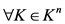 ;
;
2)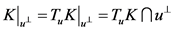 ,
, ;
;
3) ,
,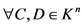 ,
,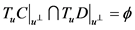 ;
;
4) ,
, 。
。
则 为
为 关于法向量
关于法向量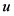 的Steiner对称。
的Steiner对称。
证明对于条件(3),我们可以由条件(2)很容易得出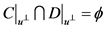 。对于条件(4),我们知道
。对于条件(4),我们知道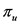 是作
是作
关于超平面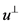 的对称变换,故很容易由(4)得出
的对称变换,故很容易由(4)得出 关于
关于 对称。则由定理3.1可得
对称。则由定理3.1可得 为
为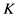 关于法向量
关于法向量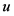 的Steiner对称。证毕。
的Steiner对称。证毕。
推论3.2 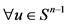 ,
, 为
为 上的映射,
上的映射,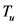 满足以下条件:
满足以下条件:
1)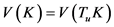 ,
,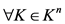 ;
;
2) ,
,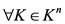 ;
;
3)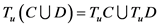 ,
,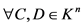 ,
,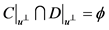 ;
;
4) 关于
关于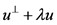 对称,
对称, ,
,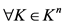 。
。
则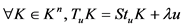 。
。
说明:推论3.2的证明由定理3.1很容易得出,这里将不再证明。
定理3.2  ,
,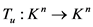 为
为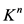 上的映射,
上的映射, 满足以下条件:
满足以下条件:
1)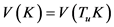 ,
,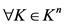 ;
;
2) ,有
,有 ;
;
3) ;
;
4)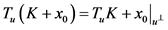 。
。
则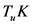 为
为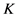 关于法向量
关于法向量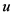 的Steiner对称。
的Steiner对称。
证明
第一步:
设 关于
关于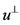 对称,由条件(3)知:
对称,由条件(3)知:
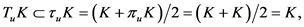
即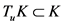 ,这里
,这里 都为紧(闭)凸集。又由(1)
都为紧(闭)凸集。又由(1)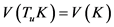 知,
知,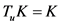 ,故有
,故有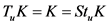 。
。
对于上述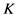 由(4)知:
由(4)知:

即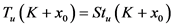 。
。
所以对于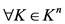 ,若
,若 ,使得
,使得 关于
关于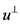 对称,则有
对称,则有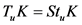 。
。
第二步:
对于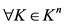 ,设
,设 ,则
,则 ,有
,有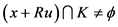 ,记
,记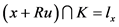 ,则有:
,则有:

由上述知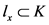 ,且
,且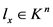 ,故由条件(2)可得
,故由条件(2)可得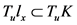 ,这里
,这里 其实为垂直于
其实为垂直于 的线段,从而由第一步的结论可知
的线段,从而由第一步的结论可知 ,由
,由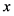 的任意性知:
的任意性知:
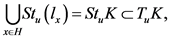
其中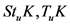 都为紧(闭)凸集,又因为
都为紧(闭)凸集,又因为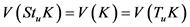 ,则
,则 。
。
综上所述 为
为 关于法向量
关于法向量 的Steiner对称。证毕。
的Steiner对称。证毕。
4. 结语
本文根据Steiner对称化的性质构造出了一个映射 ,得到了Steiner对称化在凸体上的两个充分条件。本文最大的难度就是如何确定映射
,得到了Steiner对称化在凸体上的两个充分条件。本文最大的难度就是如何确定映射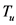 满足的条件,我们通过阅读有关Steiner对称化性质的文献,经过一系列的尝试,得到了Steiner对称化的充分条件,这使得读者可以更加具体地了解Steiner对称化。
满足的条件,我们通过阅读有关Steiner对称化性质的文献,经过一系列的尝试,得到了Steiner对称化的充分条件,这使得读者可以更加具体地了解Steiner对称化。
致谢
在这里诚挚地感谢我的导师王拓教授,无论是在理论学习,还是论文的选题,资料收集,无不得到王老师的悉心指导与帮助,在此谨向王老师致以诚挚的谢意和崇高的敬意。
文章引用
孙丽英. 凸体的Steiner对称化的两个定理
Two Theorems of Steiner Symmetrization on Convex Bodies[J]. 理论数学, 2017, 07(05): 368-372. http://dx.doi.org/10.12677/PM.2017.75047
参考文献 (References)
- 1. Gruber, P. M. (2007) Convex and Discrete Geometry. Springer, Berlin, 168-179, 120-132.
- 2. 刘越. Steiner对称化及平面上经Steiner对称化保持直径的凸集[D]: [硕士学位论文]. 广州: 中山大学, 2009.
- 3. Klain, D.A. (2011) Steiner Symmetrization Using a Finite Set of Directions. Advances in Applied Mathematics, 48, 340-353. https://doi.org/10.1016/j.aam.2011.09.004
- 4. Coupier, D. and Davydov, Y. (2014) Random Symmetrizations of Convex Bodies. Advances in Applied Probability, 46, 603-621. https://doi.org/10.1017/S000186780000728X
- 5. Bourgain, J., Lindenstrauss, J. and Milman, V. (1989) Estimates Related to Steiner Symmetrizations. In: Lindenstrauss, J. and Milman, V.D., Eds., Geometric Aspects of Functional Analysis, Lecture Notes in Mathematics, Vol. 1376, Springer, Berlin, Heidelberg, 264-273. https://doi.org/10.1007/BFb0090060
- 6. Schneider, R. (1993) Convex Bodies: The Brunn-Minkowski Theory. Cambridge University Press, Cambridge. https://doi.org/10.1007/BFb0090060
- 7. Falconer, K.J. (1976) A Result on the Steiner Symmetrization of a Compact Set. Journal of the London Mathematical Society, S2-14, 385-386. https://doi.org/10.1112/jlms/s2-14.3.385
- 8. Bianchi, G., Gardner, R.J. and Gronchi, P. (2017) Symmetrization in Geometry. Advances in Mathematics, 306, 51-88. https://doi.org/10.1016/j.aim.2016.10.003
- 9. Krantz, S.G. and Parks, H.R. (1999) The Geometry of Domains in Space. Birkhauser, Basel, 223-246. https://doi.org/10.1007/978-1-4612-1574-5
- 10. Klartag, B. (2000) Remarks on Minkowski Symmetrizations. In: Milman, V.D. and Schechtman, G., Eds., Geometric Aspects of Functional Analysis, Lecture Notes in Mathematics, Vol. 1745, Springer, Berlin, Heidelberg, 109-117. https://doi.org/10.1007/BFb0107211