Pure Mathematics
Vol.08 No.02(2018), Article ID:24032,6
pages
10.12677/PM.2018.82016
The Uniqueness of a Class of Entire Functions Sharing Small Functions
E Liang
School of Mathematics, Yunnan Normal University, Kunming Yunnan
Received: Feb. 21st, 2018; accepted: Mar. 6th, 2018; published: Mar. 14th, 2018

ABSTRACT
This paper improves the previous results, the following theorem is established: Let
and
be two non-constant entire functions, and satisfy
, where
and
are two discriminant polynomials, if
and
are IM sharing functions of
and
, and
has infinitely zero of multiplicity, then
.
Keywords:Entire Functions, Order of Growth, IM Shared Values

一类分担小函数的整函数的唯一性
梁 娥
云南师范大学数学学院研究生,云南 昆明
收稿日期:2018年2月21日;录用日期:2018年3月6日;发布日期:2018年3月14日

摘 要
本文推进了前人的结果得到如下定理成立:设
与
是两个非常数整函数,且
,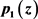 与
是两个判别多项式,若
与
以
与
为IM分担小函数,且
有无穷多个重零点,则
。
与
是两个判别多项式,若
与
以
与
为IM分担小函数,且
有无穷多个重零点,则
。
关键词 :整函数,增长极,IM分担值

Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言、相关引理及主要结果
2008年,何萍等 [1] 证明了:
定理A:设
与
是两个非常数整函数,且
,
与
是两个判别多项式,若
与
以
与
为IM分担小函数,且
有无穷多个重零点,则
。
2013年,高晓佳等 [2] 证明了:
定理B:设
与
为两个非常数整函数,且
,若
与
有两个有穷的IM分担
值
和
,则
。
在以上定理的基础上,本文做出了进一步的推进。
本文涉及的相关引理:
引理1: [3] 设
是级
且不恒为零的整函数,则
引理2: [4] 设集合
和
是
的两个可测子集,如果
,则
,且进一步有
。
引理3: [5] 设
是超越整函数,其增长极
,令
对于充分大的正数
,用
表示
所包含的最大弧的弧长(若在圆周
上都有
),那么如下两个结论中至少有一个必定成立:
1) 存在具有正的上对数密度的集合
使得:
2) 对于
有

其中
。
注:引理3是由文献 [5] 中引理2.3直接得到的。其中
为任意有穷正数,由该文献中的引理2.3可知其选取无本质差别。
引理4: [6] 设
是超越整函数,且
,则存在对数测度为有穷的集合
,使对
有
引理5: [7] 设
是超越亚纯函数,如果判别亚纯函数
为
的小函数,令
则
。
引理6: [8] 设
为非常数亚纯函数,如果判别亚纯函数
为
的小函数,令
则
。
本文证明了结果:
定理1:设
与
是两个非常数整函数,且
,
与
是两个判别多项式,若
与
以
与
为IM分担小函数,且
有无穷多个重零点,则
。
2. 定理1的证明
若
与
中至少有一个为多项式,则
与
都退化为常数,根据定理B知结论成立,故以下仅考虑
与
均为超越整函数的情形:
因为
与
都以多项式
与
为IM分担小函数,则令
其中
由引理5知
。且易证得我们令的辅助函数
实际上都是整函数。再结合引理6有
结合条件可得
,同理有
。
若
和
中至少有一个为多项式,不妨设
为多项式,结合条件
有无穷多个重零点。于是
,而由引理5知
,则
;若
为多项式,同理可得
。
若
和
均为超越整函数,我们将根据引理3分情况讨论:
情形1:
以及
使
具有正的上对数密度,不妨设
(否则
时讨论类似),则
具有正的上对数密度,且
(1)
这里的
取为大于多项式
的次数的值。
而
为超越整函数,且
,故由引理4知:
使
具有有穷的对数密度,且对
有
(2)
因为
的密度为1,从而
为无界集,故存在严格递增的无界数列
包含于
,于是
(3)
(4)
(5)
而
(6)
且由
再结合(3)、(4)、(5)得
(7)
同理,
(8)
则由(7)、(8)结合引理1知:
所以
一定是多项式,这与
为超越整函数相矛盾。
情形2:对于
,
和
满足
由于
。从而存在充分小的正数
,使
取
,有
(9)
且
,由引理2知
,故存在严格递增的无界数列
。继续令:
因为
,从而不失一般性,不妨设存在正整数列
满足
(另一情形用
换
即可),为了表述上的方便,不妨设
,于是对于一切的
有
,那么
(10)
令
。则由(9)、(10)得
。于是对于
有
故
进而有
而
是级小于1的超越整函数,故结合引理1有
这就得出矛盾。
综上所述,定理得证。
文章引用
梁 娥. 一类分担小函数的整函数的唯一性
The Uniqueness of a Class of Entire Functions Sharing Small Functions[J]. 理论数学, 2018, 08(02): 126-131. https://doi.org/10.12677/PM.2018.82016
参考文献
- 1. 何萍, 熊坚. 关于有穷级整函数的唯一性[J]. 云南师范大学学报(自然科学版), 2007, 27: 5-8.
- 2. 高晓佳, 许宇霞. 级小于 的整函数的唯一性[D]: [硕士学位论文]. 昆明: 云南师范大学, 2013.
- 3. Boas, R.P. (1954) Entire Functions. Nortbwestern University, Evanston.
- 4. 蔡翠. 一类整函数的唯一性[D]: [硕士学位论文]. 昆明: 云南师范大学, 2005.
- 5. Bergweile, W. and Lang Ley, J.K. (2007) Zeros of Differences of Meromorphic Functions. Mathematical Proceedings of the Cambridge Philosophical Society, 142, 133-147. https://doi.org/10.1017/S0305004106009777
- 6. Adams, W.W. and Straus, E.G. (1971) Non-Archimedian Analytic Functions Taking the Same Values at the Same Points. Journal of Mathematics, 15, 418-424.
- 7. 李玉华. 具有4个有穷的IM公共小函数的整函数[J]. 数学学报, 1998, 41(2): 249-260.
- 8. 李玉华. 分担4个或5个小函数的亚纯函数[J]. 数学研究与评论, 2000, 20(1): 94-96.
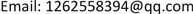



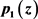 与
是两个判别多项式,若
与
以
与
为IM分担小函数,且
有无穷多个重零点,则
。
与
是两个判别多项式,若
与
以
与
为IM分担小函数,且
有无穷多个重零点,则
。


