Pure Mathematics
Vol.08 No.03(2018), Article ID:24811,5
pages
10.12677/PM.2018.83025
Study on Properties of Big Hankel Operator on Harmonic Bergman Space
Jing Yang
College of Mathematics and System Science, Shenyang Normal University, Shenyang Liaoning
Received: Apr. 18th, 2018; accepted: May 1st, 2018; published: May 10th, 2018

ABSTRACT
This article mainly discusses some of the properties of the Big Hankel operator whose symbol is a radial function on the Bergman space. It constructs a series related to its symbolic function and obtains some conclusions about the nature of the big Hankel operator. The boundedness of the big Hankel operator is equivalent to the boundedness of . The compactness of the big Hankel operator converges to zero with , and the positivity of the big Hankel operator is equivalent to the bounded sequence with greater than zero.
Keywords:Big Hankel Operators, Harmonic Bergman Spaces, Boundedness, Compactness, Positivity

调和Bergman空间上大Hankel算子性质的研究
杨静
沈阳师范大学数学与系统科学学院,辽宁 沈阳

收稿日期:2018年4月18日;录用日期:2018年5月1日;发布日期:2018年5月10日

摘 要
本篇文章主要讨论了调和Bergman空间上以径向函数为符号的大Hankel算子的一些性质,构造了一个与其符号函数相关的数列 ,得到了一些有关大Hankel算子的性质的一些结论。其有界性与 的有界性等价,其紧性与 收敛到0等价,其正定性与 为大于0的有界数列等价。
关键词 :大 算子,Bergman调和空间,有界性,紧性,正定性

Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本节中将给出一些基本的概念以及符号,方便后续使用。
设 为复平面, 为 中的单位开圆盘,使用dA定义D上的面积测度,所以规范D的面积是1,按照直角坐标和极坐标,有 ,其中 。
定义1.1:设 表示D上所有勒贝格平方可积的函数构成的集合,定义内积
则 为一个Hilbert空间。
定义1.2: 中的全体解析函数构成了Bergman空间 。
定义1.3:我们设P为 到 的正交投影,众所周知 为 的闭子空间。则有 ,其中 为Bergman空间的再生核。
定义1.4:调和Bergman空间 为D上所有调和函数构成的集合。
定义1.5:设Q表示 到 的正交投影,显然是为 的闭子空间。容易验证对任意的 ,存在 中唯一一个函数 ,使得 , ,通过计算可知 ,因此有
.
定义1.6:设 为一个酉算子,定义为
, .
定义1.7:设 , 是定义在 的乘法算子,即 。
定义1.8: ,以φ为符号的大Hankel算子定义为 。
定义1.9:若函数φ满足 ,则称φ为径向函数。下文中将用 表示D上全体径向函数构成的集合。
本篇论文主要研究以调和函数φ为符号的大Hankel算子的一些性质, [1] 中给出了调和函数以及调和Bergman空间的一些结论, [2] 中给出了以调和函数φ为符号的Toeplitz算子的一些性质的结论, [3] 研究了正定性的一些结论,本文主要根据 [4] [5] 给出的大小Hankel算子的一些性质结论为研究前提,结合 [2] 中讨论的以调和函数φ为符号Toeplitz算子来研究以调和函数φ为符号的大Hankel算子的一些性质。
2. 主要结论
本文主要讨论以径向函数为符号的大Hankel算子的一些性质。
定理2.1:设函数 ,函数 。 ,令 ,则有 。
证明:显然
因为 为径向函数,故当 时, 。
又因为 ,
因此得到 。
引理2.1 [1] :设
,
,
,
;
,
,则 为
为 的正规正交基。
的正规正交基。
2.1. 大Hankel算子的有界性
定理2.2:设函数 ,则
,则 有界当且仅当
有界当且仅当 有界。
有界。
证明:先证明必要性:假设 为有界线性算子。
为有界线性算子。
由引理2.1我们知 ,
,
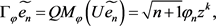
且 ,同理
,同理 ,故有
,故有 即
即 有界。
有界。
接下来证明充分性:假设 有界,且
有界,且 ,由定理2.1
,由定理2.1
设
则

而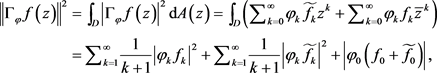
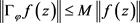
又因为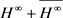 在
在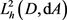 中稠密,故
中稠密,故 为有界算子。
为有界算子。
2.2. 大Hankel算子的紧性
定理2.3:设函数 ,则有
,则有 为紧算子当且仅当
为紧算子当且仅当 ,
, 。
。
证明:先证明必要性:假设 为紧算子,而正规正交基
为紧算子,而正规正交基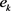 弱收敛于0,
弱收敛于0, ;且
;且 弱收敛于0,
弱收敛于0,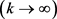 。因此有
。因此有 。
。
下面证明充分性: ,
, ,有
,有 为紧算子。
为紧算子。
若有 ,可以证明
,可以证明 。
。
因为 在
在 中稠密,因此存在序列
中稠密,因此存在序列 ,使
,使

因此 ,
, 。由定理2.1我们知道
。由定理2.1我们知道

因此 ,
, 。
。
故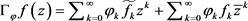 。
。
对于正整数K,定义 上算子,对
上算子,对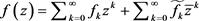 。
。
令 。
。
显然 为一个有限秩算子,因此
为一个有限秩算子,因此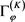 为一个紧算子。
为一个紧算子。
而 。
。
而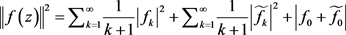 ,且
,且 ,
,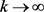 时,故
时,故 ,
, 因此
因此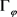 为紧算子。
为紧算子。
2.3. 大Hankel算子的正定性
定理2.4:设函数 ,则
,则 为正定的当且仅当
为正定的当且仅当 为正项数列,即
为正项数列,即 ,都有
,都有 。
。
证明:先证明必要性:设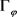 为正定的,由正定的定义我们知道,对于
为正定的,由正定的定义我们知道,对于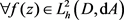 ,我们有
,我们有 ;则对于
;则对于 有
有 即
即 则一定有
则一定有 。
。
下面证明充分性: 为正项数列,即
为正项数列,即 ,都有
,都有 ;
;
任意 ,
,
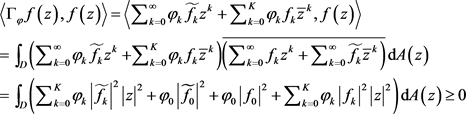
故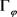 为正定。
为正定。
文章引用
杨 静. 调和Bergman空间上大Hankel算子性质的研究
Study on Properties of Big Hankel Operator on Harmonic Bergman Space[J]. 理论数学, 2018, 08(03): 203-207. https://doi.org/10.12677/PM.2018.83025
参考文献
- 1. Axler, S., Bourdon, P. and Ramey, W. (2001) Harmonic Function Theory. Springer, New York. https://doi.org/10.1007/978-1-4757-8137-3
- 2. 王晓峰, 高崇志. 调和Bergman空间上特殊符号的Toeplitz算子[J]. 四川理工学院学报(自然科学版), 2006, 19(4): 1-4.
- 3. Shu, Y.L. and Zhao, X.F. (2016) Positivity of Toeplitz Operators on Harmonic Bergman Space. Acta Mathematica Sinica, 32, 175-186. https://doi.org/10.1007/s10114-016-5138-7
- 4. 黄辉斥. Bergman空间上小Hankel算子的代数性质(英文) [J]. 复旦学报(自然科学版), 2005, 44(3): 370-374+381.
- 5. Osawa, T. (2006) Finite Rank Intermediate Hankel Operators and the Big Hankel Operator. International Journal of Mathematics and Mathematical Sciences, 2006, Article ID: 51705. https://doi.org/10.1155/IJMMS/2006/51705