ABSTRACT

In this paper, we use Nevanlinna theory to discuss the unicity problems of the finite-order transcendental meromorphic solution of Painlevé IV difference equations with another meromorphic function that share three values.

Keywords:Complex Difference Equation, Meromorphic Solution, Unicity

潘勒韦IV型差分方程亚纯解唯一性

张美娟¹，林珊华²

¹福建师范大学数学与信息学院，福建 福州

²泉州师范学院数学与计算机科学学院，福建 泉州

收稿日期：2018年10月15日；录用日期：2018年10月27日；发布日期：2018年11月8日

摘 要

本文利用Nevanlinna理论讨论了潘勒韦IV型差分方程的有限级超越亚纯解与另一个亚纯函数分担三个公共值的唯一性问题。

关键词 :复差分方程，亚纯解，唯一性

Copyright © 2018 by authors and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

本文采用Nevanlinna理论中的一些基本概念和标准符号 [1] [2] 。亚纯函数通常指定义在整个复平面上的亚纯函数。设f是亚纯函数，用 $\rho \left(f\right)$ 表示亚纯函数f的增长级，用 ${\rho }_2\left(f\right)$ 表示亚纯函数f的超级，且定义如下

${\rho }_2\left(f\right)=\underset{r\to \infty }{\lim \sup }\frac{{\log }^{+}{\log }^{+}T\left(r,f\right)}{\log r}$

定义集合 $$ 的线性测度为 $mE={\displaystyle {\int }_E\text{d}t}$，以及对数测度为 $m_{l}E={\displaystyle {\int }_E\frac{\text{d}t}{t}}$ 。如果亚纯函数a满足 $T\left(r,a\right)=S\left(r,f\right)$，其中 $S\left(r,f\right)=o\left(T\left(r,f\right)\right)\left(r\to \infty \right)$，那么称a是f的小函数，可能需除去一对数测度有限的例外集。设f和g为非常数亚纯函数，a为任意复数，如果 $f-a$ 与 $g-a$ 的零点相同并计重数，则称f与gCM分担a。如果f与g的极点相同并计重数，则称f与gCM分担 $\infty$ 。

潘勒韦方程是一类物理背景深厚且应用广泛的重要方程。近十年来，人们通过引入Nevanlinna 理论深入研究了复域微分和差分方程，并取得了一些优秀的成果。随着Halburd和Korhonen [3] 以及Chiang和Feng [4] 的奠基性研究型成果的出现，促进了差分的Nevanlinna理论的建立以及潘勒韦差分方程的发展。而后，Halburd [5] ，Ronkainen [6] ，张继龙 [7] 等人对非线性差分方程进行了分类，给出了几类差分Riccati方程和潘勒韦I-V型差分方程。

设 $$ 均是f的小函数，记 $R\left(z,f\right)=\frac{P\left(z,f\right)}{Q\left(z,f\right)}$ 是关于z亚纯，关于f有理的函数，其中 $$，并且 $P\left(z,f\right),Q\left(z,f\right)$ 的次数分别为 $\mathrm{deg}P\left(z,f\right)=m,\mathrm{deg}Q\left(z,f\right)=n$ 。

汪晓明 [8] 等人研究了潘勒韦III型差分方程

$f\left(z+1\right)f\left(z-1\right)=R\left(z,f\right)$

的有限级超越亚纯函数解的唯一性，证明了在一定条件下，如果潘勒韦III型差分方程的有限级超越亚纯解f与另一个亚纯函数g有两个不同的有限分担值并且有完全相同的极点(计重数)，那么 $f\equiv g$ 。

1991年，Ramani [9] 考察了潘勒韦IV型差分方程 $\left(f\left(z+1\right)+f\left(z\right)\right)\left(f\left(z-1\right)+f\left(z\right)\right)=R\left(z\right)$，其中该方程的所有系数均为常数且 $R\left(z\right)$ 是关于z有理的函数。

本文，我们将 $R\left(z\right)$ 推广至 $R\left(z,f\right)$，进而研究了以下潘勒韦IV型差分方程

$$ (1.1)

的有限级超越亚纯函数解的唯一性问题，又置

$\varphi \left(z,f\right)=\left(f\left(z+1\right)+f\left(z\right)\right)\left(f\left(z-1\right)+f\left(z\right)\right)Q\left(z,f\right)-P\left(z,f\right)$ (1.2)

我们得到了如下定理：

定理1.1：设f是差分方程(1.1)的有限级超越亚纯函数解，g是一个亚纯函数， $m,n$ 为正整数且满足 $m=n+2$ 。 $e_1,e_2$ 为两个互异的有穷复数， $\varphi \left(z,f\right)$ 如(1.2)所示，若f和gCM分担 $e_1,e_2,\infty$，且 $\varphi \left(z,e_1\right)\cancel{\equiv }0,\varphi \left(z,e_2\right)\cancel{\equiv }0$，则 $f\equiv g$ 。

2. 引理

首先，亚纯函数f的差分多项式 $H\left(z,f\right)$ 定义如下：

$H\left(z,f\right)={\displaystyle \underset{\lambda \in J}{\sum }{a}_{\lambda }}\left(z\right){\displaystyle \underset{j=1}{\overset{{\tau }_{\lambda }}{\prod }}f{\left(z+{\delta }_{\lambda ,j}\right)}^{{\mu }_{\lambda ,j}}},$ (2.1)

其中，J是指标集， ${\delta }_{\lambda ,j}$ 是复常数， $$ 是非负整数，系数 $a_{\lambda }\left(z\right)\left(\cancel{\equiv }0\right)$ 是f的小函数。对 $H\left(z,f\right)$ 的每一个单项式 ${\displaystyle {\sum }_{j=1}^{{\tau }_{\lambda }}f{\left(z+{\delta }_{\lambda ,j}\right)}^{{\mu }_{\lambda ,j}}}$，定义其次数为 $d_{\lambda }={\displaystyle {\sum }_{j=1}^{{\tau }_{\lambda }}{\mu }_{\lambda ,j}}$ 。并定义 $H\left(z,f\right)$ 的次数为

${\mathrm{deg}}_{f}H\left(z,f\right)=\underset{\lambda \in J}{\max }\left\{d_{\lambda }\right\}.$

接下来，为证明定理1.1，我们需要下列一些引理。

引理2.1 [10] 设f是超级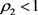的非常数亚纯函数，c是一非零有穷复数，则存在正数 $\epsilon >0$，使得

$m\left(r,\frac{f\left(z+c\right)}{f\left(z\right)}\right)=o\left(\frac{T\left(r,f\right)}{r^{1-{\rho }_2-\epsilon }}\right)=S\left(r,f\right)$

对所有r成立，至多除去一个对数测度为有限的集合。

引理2.2设f是超级 ${\rho }_2<1$ 的超越亚纯函数，且满足差分方程 $$，其中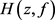如(2.1)所定义。设a为f的小函数且满足 $H\left(z,a\right)\cancel{\equiv }0$，则

对所有r成立，至多除去一个对数测度为有限的集合。

证明：令 $f=g+a$，并代入差分方程 $H\left(z,f\right)=0$ 中，于是得到

$L\left(z,g\right)+D\left(z\right)=0,$

其中 $L\left(z,g\right)={\displaystyle {\sum }_{\gamma }{b}_{\gamma }\left(z\right)G_{\gamma }\left(z,g\right)}$，其每一项都是次数不小于1的关于g的多项式，且 $T\left(r,D\right)=o\left(T\left(r,g\right)\right)$，显然 $D\left(z\right)\cancel{\equiv }0$，否则 $D\left(z\right)\equiv 0$，有 $L\left(z,0\right)\equiv 0$，即 $H\left(z,a\right)\equiv 0$，与题设矛盾。

接下来，我们来讨论 $m\left(r,\frac{1}{g}\right)$ 的情况。首先，记 $E_1=\left\{z|\left|z\right|=r且\left|g\left(z\right)\right|\le 1\right\}$， $E_{\text{2}}=\left\{z|\left|z\right|=r且\left|g\left(z\right)\right|>1\right\}$，则当 $z\in E_1$ 时，由

$\left|\frac{L\left(z,g\right)}{g\left(z\right)}\right|=\frac{1}{\left|g\left(z\right)\right|}{\displaystyle \underset{\gamma }{\sum }{b}_{\gamma }}\left(z\right)g{\left(z\right)}^{l_0}g{\left(z+c_1\right)}^{l_1}\cdots g{\left(z+c_{\nu }\right)}^{l_{\nu }}\le {{\displaystyle \underset{\gamma }{\sum }\left|b_{\gamma }\left(z\right)\right|\left|\frac{g\left(z+c_1\right)}{g\left(z\right)}\right|}}^{l_1}\cdots {\left|\frac{g\left(z+c_{\nu }\right)}{g\left(z\right)}\right|}^{l_{\nu }},$

其中 ${\displaystyle {\sum }_{j=0}^{\nu }{l}_j}\ge 1$ 。再由引理2.1，有

$\begin{array}{c}m\left(r,\frac{L}{g}\right)\le m\left(r,{{\displaystyle \underset{\gamma }{\sum }\left|b_{\gamma }\left(z\right)\right|\left|\frac{g\left(z+c_1\right)}{g\left(z\right)}\right|}}^{l_1}\cdots {\left|\frac{g(z+c_{\nu })}{g\left(z\right)}\right|}^{l_{\nu }}\right)\le {\displaystyle \underset{\gamma }{\sum }m\left(r,b_{\gamma }\left(z\right){\left|\frac{g\left(z+c_1\right)}{g\left(z\right)}\right|}^{l_1}\cdots {\left|\frac{g\left(z+c_{\nu }\right)}{g\left(z\right)}\right|}^{l_{\nu }}\right)}\\ ={\displaystyle \underset{\gamma }{\sum }\frac{1}{\text{2π}}{\displaystyle {\int }_0^{\text{2π}}{\log }^{+}\left|b_{\gamma }\left(r{e}^{i\theta }\right){\left|\frac{g\left(r{e}^{i\theta }+c_1\right)}{g\left(r{e}^{i\theta }\right)}\right|}^{l_1}\cdots {\left|\frac{g\left(r{e}^{i\theta }+c_{\nu }\right)}{g\left(r{e}^{i\theta }\right)}\right|}^{l_{\nu }}\right|\text{d}\theta }}\\ \le {\displaystyle \underset{\gamma }{\sum }\left(m\left(r,b_{\gamma }\left(z\right)\right)+l_{1}m\left(r,\frac{g\left(z+c_1\right)}{g\left(z\right)}\right)+\cdots +l_{\nu }m\left(r,\frac{g\left(z+c_{\nu }\right)}{g\left(z\right)}\right)\right)}=S\left(r,f\right),\end{array}$

则可得到

$I_1=\frac{1}{\text{2π}}{\displaystyle {\int }_0^{\text{2π}}{\log }^{+}}\left|\frac{1}{g\left(r{\text{e}}^{i\theta }\right)}\right|\text{d}\theta \le m\left(r,\frac{D}{g}\right)+m\left(r,\frac{1}{D}\right)=m\left(r,\frac{L}{g}\right)+m\left(r,\frac{1}{D}\right)=S\left(r,f\right).$ (2.2)

而当 $z\in E_2$ 时，

$I_{\text{2}}=\frac{1}{2\text{π}}{\displaystyle {\int }_0^{\text{2π}}{\log }^{+}}\left|\frac{1}{g\left(r{e}^{i\theta }\right)}\right|\text{d}\theta =0.$ (2.3)

所以由(2.2)及(2.3)，可得

$m\left(r,\frac{1}{f-a}\right)=I_1+I_2=S\left(r,f\right).$

得证。

引理2.3 [7] 设f是超级 ${\rho }_2<1$ 的亚纯函数，且满足差分方程 $H\left(z,f\right)Q\left(z,f\right)=P\left(z,f\right)$，其中 $$ 如(2.1)所示， $P\left(z,f\right),Q\left(z,f\right)$ 是f的多项式，如(1.1)所示，若

${\mathrm{deg}}_{f}H\left(z,f\right)<\max \left\{\mathrm{deg}P\left(z,f\right),\mathrm{deg}Q\left(z,f\right)\right\},$

则 $m\left(r,f\right)=S\left(r,f\right)$ 。

引理2.4 [11] 设h为非常数整函数， $f=e^h$， $\rho$ 和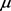分别表示f的级和下级，

i) 若h为p次多项式，则 $$ ；

ii) 若h为超越亚纯函数，则 $\rho =\mu =\infty$ 。

引理2.5 [11] 设 $f_j\left(j=1,2,\cdots ,n\right)$ 于开平面亚纯， $f_k\left(k=1,2,\cdots ,n-1\right)$ 不为常数， $$ 且满足

${\displaystyle \underset{j=1}{\overset{n}{\sum }}{f}_j}\equiv 1,$

其中 $n\ge 3$ 。如果，且

${\displaystyle \underset{j=1}{\overset{n}{\sum }}N\left(r,\frac{1}{f_j}\right)}+\left(n-1\right){\displaystyle \underset{j=1}{\overset{n}{\sum }}\bar{N}\left(r,f_j\right)}<\left(\lambda +o\left(1\right)\right)T\left(r,f_k\right)\left(r\in I,k=1,2,\cdots ,n-1\right),$

其中 $\lambda <1$，则 $f_n\equiv 1$ 。

3. 定理1.1的证明

由假设条件 $$ 及引理2.2，有

$m\left(r,\frac{1}{f-e_1}\right)=S\left(r,f\right),m\left(r,\frac{1}{f-e_2}\right)=S\left(r,f\right).$ (3.1)

另外，由Nevanlinna第二基本定理

$\begin{array}{c}T\left(r,f\right)\le N\left(r,f\right)+N\left(r,\frac{1}{f-e_1}\right)+N\left(r,\frac{1}{f-e_2}\right)+S\left(r,f\right)\\ \le N\left(r,g\right)+N\left(r,\frac{1}{g-e_1}\right)+N\left(r,\frac{1}{g-e_2}\right)+S\left(r,f\right)\\ \le 3T\left(r,g\right)+S\left(r,f\right),\end{array}$ (3.2)

同理可证

$$ (3.3)

所以

$\rho \left(f\right)=\rho \left(g\right).$ (3.4)

假设

$\frac{f-e_1}{g-e_1}=e^A,\frac{f-e_2}{g-e_2}=e^B,$ (3.5)

其中， $A,B$ 是两个关于z的多项式。如果 $e^A\equiv 1$，或者 $e^B\equiv 1$，或者 $$ 时，则显然 $f\equiv g$ 。

下面假设 $e^A\cancel{\equiv }1$， $e^B\cancel{\equiv }1$，且 $e^{B-A}\cancel{\equiv }1$ 。则由(3.2)，(3.3)以及(3.5)可得

$T\left(r,e^A\right)\le 4T\left(r,f\right)+S\left(r,f\right),$

$T\left(r,e^B\right)\le 4T\left(r,f\right)+S\left(r,f\right).$ (3.6)

因此 $\max \left\{\rho \left(e^A\right),\rho \left(e^B\right)\right\}\le \rho \left(f\right)$ 。

令 $C=B-A$，则由(3.5)式可得

$f=e_1+\left(e_2-e_1\right)\frac{e^B-1}{e^C-1},$ (3.7)

或

$f=e_{\text{2}}+\left(e_2-e_1\right)\frac{e^A-1}{e^C-1}{e}^C.$ (3.8)

于是由(3.7)可得

$T\left(r,f\right)\le T\left(r,e^C\right)+T\left(r,e^B\right)+S\left(r,f\right),$ (3.9)

所以，又 $$，故 $\rho \left(f\right)=\max \left\{\rho \left(e^A\right),\rho \left(e^B\right)\right\}$ 。

下面我们证明 $$ 。首先，我们假设

$e^B-1=D{B}_1,e^C-1=D{C}_1,$

其中， $$ 均为整函数，于是(3.7)可以写成

结合(3.1)式子可得

$T\left(r,f\right)=m\left(r,\frac{1}{f-e_1}\right)+N\left(r,\frac{1}{f-e_1}\right)+S\left(r,f\right)=N\left(r,\frac{1}{B_1}\right)+S\left(r,f\right).$ (3.10)

由条件 $$，所以由引理2.3有 $m\left(r,f\right)=S\left(r,f\right)$，故

$T\left(r,f\right)=m\left(r,f\right)+N\left(r,f\right)=N\left(r,\frac{1}{C_1}\right)+S\left(r,f\right).$ (3.11)

另外由第二基本定理可得

$T\left(r,e^B\right)\le N\left(r,e^B\right)+N\left(r,\frac{1}{e^B}\right)+N\left(r,\frac{1}{e^B-1}\right)+S\left(r,e^B\right)=N\left(r,\frac{1}{e^B-1}\right)+S\left(r,f\right)\le T\left(r,e^B\right)+S\left(r,f\right),$

又

$N\left(r,\frac{1}{e^B-1}\right)=N\left(r,\frac{1}{B_1}\right)+N\left(r,\frac{1}{D}\right)+S\left(r,f\right),$

所以

$T\left(r,e^B\right)=N\left(r,\frac{1}{B_{\text{1}}}\right)+N\left(r,\frac{1}{D}\right)+S\left(r,f\right).$ (3.12)

同理可证得

$T\left(r,e^C\right)=N\left(r,\frac{1}{C_{\text{1}}}\right)+N\left(r,\frac{1}{D}\right)+S\left(r,f\right).$ (3.13)

于是，由(3.10)~(3.13)有

$T\left(r,e^C\right)=T\left(r,e^B\right)+S\left(r,f\right).$ (3.14)

对(3.8)式类似分析可得

$T\left(r,e^C\right)=T\left(r,e^A\right)+S\left(r,f\right).$ (3.15)

因此，由(3.14)及(3.15)可得

$\rho \left(e^A\right)=\rho \left(e^B\right)=\rho \left(e^C\right)=\rho \left(f\right),$ (3.16)

又由于 $$ 为非常数多项式，不妨设 $\mathrm{deg}\left(A\right)=d$，d是一个非零正整数，则由引理2.4及(3.16)式得

$\mathrm{deg}\left(A\right)=\mathrm{deg}\left(B\right)=\mathrm{deg}\left(C\right)=d.$ (3.17)

接下来，我们引入 $\bar{f}=f\left(z+1\right),\underset{\_}{f}=f\left(z-1\right)$，则将(3.7)式代入(1.1)式中得

$\begin{array}{l}\left[2e_1+\left(e_2-e_1\right)\left(\frac{e^{\bar{B}}-1}{e^{\bar{C}}-1}+\frac{e^B-1}{e^C-1}\right)\right]\left[2e_1+\left(e_2-e_1\right)\left(\frac{e^{\underset{\_}{B}}-1}{e^{\underset{\_}{C}}-1}+\frac{e^B-1}{e^C-1}\right)\right]{\displaystyle \underset{j=0}{\overset{n}{\sum }}{b}_j}{\left[e_1+\left(e_2-e_1\right)\frac{e^B-1}{e^C-1}\right]}^j\\ ={\displaystyle \underset{i=0}{\overset{m}{\sum }}{a}_i}{\left[e_1+\left(e_2-e_1\right)\frac{e^B-1}{e^C-1}\right]}^i\end{array}$

又注意到 $m=n+2$，于是等式两边同时乘以 $$，则可化为

$\begin{array}{l}\left\{2e_1\left(e^{\bar{C}}-1\right)\left(e^C-1\right)+\left(e_2-e_1\right)\left[\left(e^{\bar{B}}-1\right)\left(e^C-1\right)+\left(e^B-1\right)\left(e^{\bar{C}}-1\right)\right]\right\}\\ \cdot \left\{2e_1\left(e^{\underset{\_}{C}}-1\right)\left(e^C-1\right)+\left(e_2-e_1\right)\left[\left(e^{\underset{\_}{B}}-1\right)\left(e^C-1\right)+\left(e^B-1\right)\left(e^{\underset{\_}{C}}-1\right)\right]\right\}\\ \cdot {\displaystyle \underset{j=0}{\overset{n}{\sum }}{b}_j}{\left[e_1\left(e^C-1\right)+\left(e_2-e_1\right)\left(e^B-1\right)\right]}^j{\left(e^C-1\right)}^{m-j}\\ =\left(e^{\bar{C}}-1\right)\left(e^{\underset{\_}{C}}-1\right){\displaystyle \underset{i=0}{\overset{m}{\sum }}{a}_i}{\left[e_1\left(e^C-1\right)+\left(e_2-e_1\right)\left(e^B-1\right)\right]}^i{\left(e^C-1\right)}^{m-i+2}\end{array}$ (3.18)

令 $\bar{B}=B\left(z+1\right)=B\left(z\right)+s_1\left(z\right)$， $\underset{\_}{B}=B\left(z-1\right)=B\left(z\right)+s_2\left(z\right)$， $\bar{C}=C\left(z+1\right)=C\left(z\right)+t_1\left(z\right)$， $\underset{\_}{C}=C\left(z-1\right)=C\left(z\right)+t_2\left(z\right)$ 。其中 $s_1\left(z\right),s_2\left(z\right),t_1\left(z\right),t_2\left(z\right)$ 均为次数至多是 $d-1$ 的多项式，于是(3.18)整理可得

${\displaystyle \underset{\mu =0}{\overset{m}{\sum }}{\displaystyle \underset{\lambda =0}{\overset{m+2}{\sum }}{M}_{\mu ,\lambda }}}{e}^{\mu B+\lambda C}+4e_2^2{\displaystyle \underset{j=0}{\overset{n}{\sum }}{b}_j}{e}_2{}^j-{\displaystyle \underset{i=0}{\overset{m}{\sum }}{a}_i}{e}_2^i=0,$ (3.19)

其中 $\mu ,\lambda$ 不同时为零， $M_{\mu ,\lambda }$ 为关于 $$ 的多项式。

特别地，计算可知

$$ (3.20)

于是，等式(3.19)两边同时除以 $\varphi \left(z,e_2\right)$，并且移项得

$-{\displaystyle \underset{\mu =0}{\overset{m}{\sum }}{\displaystyle \underset{\lambda =0}{\overset{m+2}{\sum }}\frac{M_{\mu ,\lambda }{e}^{\mu B+\lambda C}}{\varphi \left(z,e_2\right)}}}\equiv 1,$ (3.21)

不妨记 $f_l{}^{*}=-\frac{M_{\mu ,\lambda }}{\varphi \left(z,e_2\right)}{e}^{\mu B+\lambda C}$，则(3.21)可以写成 ${\displaystyle {\sum }_{l=1}^q{f}_l{}^{*}}\equiv 1$，其中q是一个有穷正整数。

而且，当 $\mu \lambda \ne 0$ 时，我们断言

$\mathrm{deg}\left(\mu B+\lambda C\right)=d.$

事实上，当 $$ 时，则 $e^{\mu B+\lambda C}$ 是 $e^A$ 和f的小函数，于是

$T\left(r,e^{\mu B+\lambda C}{e}^{-\mu A}\right)=T\left(r,e^{-\mu A}\right)+S\left(r,f\right)=\mu T\left(r,e^A\right)+S\left(r,f\right),$

又

$T\left(r,e^{\mu B+\lambda C}{e}^{-\mu A}\right)=T\left(r,e^{\left(\mu +\lambda \right)C}\right)+S\left(r,f\right)=\left(\mu +\lambda \right)T\left(r,e^A\right)+S\left(r,f\right),$

所以 $T\left(r,e^A\right)=S\left(r,f\right)$，矛盾，故 $\mathrm{deg}\left(\mu B+\lambda C\right)=d$ 。

最后，由 $M_{\mu ,\lambda }$ 的定义，有 $\rho \left(-\frac{M_{\mu ,\lambda }}{\varphi \left(z,e_2\right)}\right)=\rho \left(M_{\mu ,\lambda }\right)<\rho \left(e^{\mu B+\lambda C}\right)$，所以 $\rho \left(-\frac{M_{\mu ,\lambda }}{\varphi \left(z,e_2\right)}\right)\le d-1$ 。又 $\rho \left(f_l{}^{*}\right)=\rho \left(e^{\mu B+\lambda C}\right)=d$，其中 $$ 。所以由 $\rho \left(-\frac{M_{\mu ,\lambda }}{\varphi \left(z,e_2\right)}\right)<\rho \left(f_l{}^{*}\right)$，可得 $T\left(r,-\frac{M_{\mu ,\lambda }}{\varphi \left(z,e_2\right)}\right)=S\left(r,f_l{}^{*}\right)$，进而可以得到，对任意的 $k=1,2,\cdots ,q$，有

$N\left(r,\frac{1}{f_k^{\ast }}\right)=S\left(r,f_l^{\ast }\right),\bar{N}\left(r,f_k^{\ast }\right)=S\left(r,f_l^{\ast }\right),$

于是，存在一个 $\tau <1$，使得

${\displaystyle \underset{k=1}{\overset{q}{\sum }}N\left(r,\frac{1}{f_k^{\ast }}\right)}+\left(q-1\right){\displaystyle \underset{k=1}{\overset{q}{\sum }}\bar{N}\left(r,f_k^{\ast }\right)}<\left(\tau +o\left(1\right)\right)T\left(r,f_l^{\ast }\right),$

故由引理2.5，可知 $f_q^{\ast }\equiv 1$，即存在，使得

$-\frac{M_{\mu ,\lambda }}{\varphi \left(z,e_2\right)}{e}^{\mu B+\lambda C}\equiv 1.$

即 $\rho \left(-\frac{M_{\mu ,\lambda }}{\varphi \left(z,e_2\right)}\right)=\rho \left(e^{\mu B+\lambda C}\right)$，矛盾，故假设不成立。

至此，定理1.1证毕。

基金项目

本论文得到福建省中青年教师教育科研项目(JA15394)和福建自然科学基金项目(2018R0038)的资助。

文章引用

张美娟,林珊华. 潘勒韦IV型差分方程亚纯解唯一性
The Unicity of the Meromorphic Solutions of Painlevé IV Difference Equations[J]. 理论数学, 2018, 08(06): 596-603. https://doi.org/10.12677/PM.2018.86080

参考文献