Pure Mathematics
Vol.
09
No.
03
(
2019
), Article ID:
30067
,
5
pages
10.12677/PM.2019.93032
Sharp Inequalities and Application of the Generalized Grötzsch Ring Function
Fei Wang1*, Peigui Zhou2, Xiaoyu Wang1
1Teaching Section of Mathematics, Zhejiang Institute of Mechanical and Electrical Engineering, Hangzhou Zhejiang
2Keyi College of Zhejiang Sci-Tech University, Shangyu Zhejiang

Received: Apr. 9th, 2019; accepted: Apr. 20th, 2019; published: May 5th, 2019

ABSTRACT
In this paper, we study some monotonicity properties of certain functions defined in term of generalized Grötzsch ring function and some elementary functions, and get new sharp inequalities. Furthermore, we also obtain the lower bound of generalized Hersch-Pfluger distortion function by applying these results in Ramanujan modular equation theory.
Keywords:Generalized Grötzsch Ring Function, Sharp Inequality, Ramanujan Modular Equations, Generalized Hersch-Pfluger Distortion Function
广义Grötzsch环函数的精确界及应用
王飞1*,周培桂2,王晓宇1
1浙江机电职业技术学院数学教研室,浙江 杭州
2浙江理工大学科技与艺术学院,浙江 上虞

收稿日期:2019年4月9日;录用日期:2019年4月20日;发布日期:2019年5月5日

摘 要
本文研究广义Grötzsch环函数与一些初等函数组合的单调性,并由此获得新的精确不等式。同时,将所得结果应用于Ramanujan模方程理论,获得广义Hersch-Pfluger偏差函数新的下界。
关键词 :广义Grötzsch环函数,精确不等式,Ramanujan模方程,广义Hersch-Pfluger偏差函数

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在本文中,arthr表示反双曲正切函数。对
,记
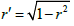 。对于正实数x和y,Γ-函数、B-函数以及ψ-函数分别定义 [1] 为:
。对于正实数x和y,Γ-函数、B-函数以及ψ-函数分别定义 [1] 为:
(1)
令 ,是Euler-Mascheroni常数,则
, (2)
在 上定义Ramanujan常数 [2] [3] 为:
(3)
当 时,式(3)记为
,
结合式(2)~(3)知 。
给定实数a,b, ,高斯超几何函数定义 [4] 为:
, (4)
这里,当 时, ,且 。
当 ,第一类、第二类广义椭圆积分分别定义 [5] 为:
(5)
(6)
因广义椭圆积分关于参数a的对称性,本文只考虑 的情形。特别地,当 时, 与 分别为第一类和第二类完全椭圆积分。
广义Grötzsch环函数 定义 [6] 为:
(7)
显然,当 时, 表示平面拟共形映射单调递减的Grötzsch极值环 的模,这里的 表示平面单位圆盘,且 , 。近几年,国内外很多学者对广义Grötzsch环函数的单调性、凹凸性及不等式进行研究,见文献 [7] [8] [9] 。
符号差 的p次广义Ramanujan模方程定义 [5] 为:
(8)
利用式(5)及式(7),可将式(8)改写成
(9)
式(9)的解可以表示为
, (10)
称式(10)中的函数 为广义Hersch-Pfluger偏差函数, , 。当 时, 退化为Hersch-Pfluger偏差函数 。此外,许多学者对广义Hersch-Pfluger偏差函数的性质做了深入的研究,见文献 [10] [11] 。
在文 [6] 中,裘松良获得如下结论:当 , 时,不等式成立
当 时等号成立,其中 。
在文 [7] 中,王根娣等揭示了广义Hersch-Pfluger偏差函数与广义Grötzsch环函数 的关系:
(11)
当且仅当 。
本文主要揭示广义Grötzsch环函数的分析性质,获得新的精确不等式,并应用于Ramanujan模方程解的精确估计。
2. 引理
本文为了证明第三部分的主要结果和引用方便,需要引入下面的导数公式 [4] :
, (12)
(13)
引理1 ( [4] , Theorem 1.25)对 ,设f和g是两个实值函数,并都在 上连续,在 (a,b)上可微且在 上 ,如果 在 上单调递增(递减),那么函数
和
也在 上单调递增(递减)。而且,若 的单调性是严格的,则F和G的单调性也是严格的。
引理2 ( [5] , Lemma 5.4)对任意的 及 ,则
(1) 从 到 上严格单调递增。
(2) 从 到 上严格单调递减。
引理3 ( [11] ,定理2.1(3))对任意的 及 ,则 从 到 上严格单调递增。
3. 主要结果及证明
利用上述引理,本节给出主要结果及证明。
定理3.1 设 ,则函数
从 到 上严格单调递增。特别地,当 时,
(14)
证明:令 , ,则 , 。由式(12)、(13),求导得
根据引理2.2 (1)、(2)及引理2.3可知, 是三个正的单调递增函数的乘积。由引理2.1可得函数 的单调性。显然, 。根据l’Hôpital法则,结合引理2.1~2.3,极限
.
显然,不等式(14)成立。
定理3.2设 , , ,则函数
从 到 上严格单调递增。特别地,当 时,
(15)
证明:令
,
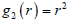 ,则
,则
 ,
。结合式(13),求导得
,
。结合式(13),求导得
由文 [7] 中定理1 (1)和引理2.1 (3)、引理2 (2)可知, 是四个正的且单调递增的函数乘积。结合引理2.1可知 的单调性。极限值 。结合文 [7] 中引理2.1 (3)、引理2 (2),运用l’Hôpital法则便知
.
推论3.3对所有的 和 时,成立不等式
(16)
特别地当 时,不等式退化为
(17)
证明:根据式(11)及定理3.2的结论易得不等式(16)和(17)。
基金项目
浙江省教育厅科研基金项目(Y201635387),浙江机电职业技术学院科研项目(A027117021),浙江省高等学校访问学者项目(FX2018093)。
文章引用
王 飞,周培桂,王晓宇. 广义GrO¨tzsch环函数的精确界及应用
Sharp Inequalities and Application of the Generalized GrO¨tzsch Ring Function[J]. 理论数学, 2019, 09(03): 254-258. https://doi.org/10.12677/PM.2019.93032
参考文献
- 1. Abramwitz, M. and Stegun, I.A. (1965) Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables. Dover Publications, New York, 253-294.
- 2. Qiu, S.L. and Vuorinen, M. (2005) Special Functions in Geometric Function Theory. In: Kühnau, R., Handbook of Complex Analysis: Geometric Function Theory, Elsevier, Amsterdam, 621-659.
https://doi.org/10.1016/S1874-5709(05)80018-6 - 3. Qiu, S.L., Ma, X.Y. and Huang, T.R. (2017) Some Proper-ties of the Difference between the Ramanujan Constant and Beta Function. Journal of Mathematical Analysis and Ap-plications, 40, 114-129.
https://doi.org/10.1016/j.jmaa.2016.08.043 - 4. Anderson, G.D., Vamanamurthy, M.K. and Vuorinen, M. (1997) Conformal Invariants, Inequalities, and Quasiconformal Maps. John Wiley & Sons, New York, 32-47.
- 5. Anderson, G.D., Qiu, S.L., Vamanamurthy, M.K., et al. (2000) Generalized Elliptic Integrals and Modular Equations. Pacific Journal of Mathematic, 192, 1-37.
https://doi.org/10.2140/pjm.2000.192.1 - 6. 裘松良. GrÖtzsch环与Ramanujan模方程[J]. 数学学报, 2000, 43(2): 283-290.
- 7. Wang, G.D., Zhang, X.H. and Chu, Y.M. (2007) Ine-qualities for the Generalized Elliptic Integrals and Modular Functions. Journal of Mathematical Analysis and Applications, 331, 1275-1283.
https://doi.org/10.1016/j.jmaa.2006.09.070 - 8. Alzer, H. and Richards, K. (2015) On the Modulus of the GrÖtzsch Ring. Journal of Mathematical Analysis and Applications, 432, 134-141.
https://doi.org/10.1016/j.jmaa.2015.06.057 - 9. Zhang, X.H. (2017) On the Generalized Modulus. The Ramanu-jan Journal, 43, 405-413.
- 10. Ma, X.Y., Chu, Y.M. and Wang, F. (2013) Monotonicity and Inequalities for the Gen-eralized Distortion Function. Acta Mathematica Scientia, 33, 1759-1766.
https://doi.org/10.1016/S0252-9602(13)60121-6 - 11. 张孝惠, 王根娣, 褚玉明, 等. 广义偏差函数的单调性和不等式[J]. 数学年刊, 2007, 28(2): 183-190.
NOTES
*通讯作者。