Pure Mathematics
Vol.
09
No.
10
(
2019
), Article ID:
33289
,
9
pages
10.12677/PM.2019.910138
Infinitely Many Solutions for Quasilinear Elliptic Equations with Φ-Laplacian Operator
Mingmin Wang*, Gao Jia
College of Science, University of Shanghai for Science and Technology, Shanghai

Received: Nov. 14th, 2019; accepted: Nov. 27th, 2019; published: Dec. 4th, 2019

ABSTRACT
By using fountain theorem, we studied a class of the Dirichlet boundary value problems of quasilinear elliptic equation with Φ-Laplacian operator. Without the Ambrosetti-Rabinowitz condition, we obtained infinitely many weak solutions.
Keywords:Quasilinear Elliptic Equation, Concave-Convex Nonlinearity, Fountain Theorem
含Φ-Laplace算子的拟线性椭圆型方程的无穷多解
王明旻*,贾高
上海理工大学理学院,上海

收稿日期:2019年11月14日;录用日期:2019年11月27日;发布日期:2019年12月4日

摘 要
本文利用喷泉定理讨论了一类具有Φ-Laplacian算子的拟线性椭圆型方程Dirichlet问题,在非线性项不满足(AR)条件的情况下,得到无穷多解的存在性。
关键词 :拟线性椭圆型方程,凹凸非线性项,喷泉定理

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文考虑如下带有Dirichlet边界的拟线性椭圆型方程存在无穷多解:
(1)
其中
是一个具有光滑边界的有界区域,
是Φ-Laplace算子,
是奇函数,
, 是连续函数,
。
在过去几十年里,对具有Φ-Laplace算子的拟线性椭圆型方程解的存在性等相关问题得到了广泛研究,如文献 [1] [2]。并且这类方程有很好的物理背景,在偏微分方程、非牛顿流体、图像处理、等离子物理等领域有着广泛的应用。近年来,讨论无穷多解存在性的文章有很多,如文献 [3] [4],分别研究了方程和方程组解的存在性和多重性问题,其中具有代表性的结果是
(2)
作者Chung [5] 等利用山路定理和喷泉引理研究了问题(2)非平凡弱解和无穷解序列的存在性问题。
本文的目的是在没有(AR)条件的情况下得到问题(1)的无穷多解的存在性。
首先,给出函数
满足下列假设:
当
时,
,当
时,
;
在
上严格增的;
,其中
, ;
存在常数
,使得对任意的
,,有
,
其中
。
进一步,假设
是连续函数且满足下面条件:
f满足次临界增长条件,即对任意的
,有
,
其中
, ;
对几乎所有
一致成立;
存在常数
,使得对任意的
,有
,,
其中
, ;
,。
假设f在无穷远处m次超线性增长,即
,但不满足(AR)条件(见文献 [6] ),这对我们解决问题造成了困难。为了克服这一困难,我们需要证明
条件,从而利用喷泉定理,得到问题(1)的无穷多解的存在性。
本文的主要结果如下:
定理1.1:在满足
和
假设下,问题(1)对任意的
,有无穷解序列
满足
,。
2. 预备知识和基本引理
记
,在
上定义Luxemburg范数:
。
记
,在
上定义范数:
。
记
是
在
中的闭包。设
满足
-条件,即
,,则
和
是可分、自反的Banach空间(见文献 [7] )。
设
,则对任意
,有
,那么
。因此,定义在
上的范数
与
等价。
设
,且当
时,
。如果对于所有的
,都有
,则称函数
在无穷远处比
增长得更慢,记
。如果
,则
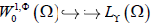 。进一步,有
。进一步,有
 。在条件
下,有连续嵌入:
。在条件
下,有连续嵌入:

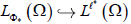 。
。
注记2.1:在条件
下,可推得下式成立:
,,。
下面给出本文需要的几个基本引理。
引理2.2 [1]:设
成立,对所有的
,令
,。
则对于任意
,,成立
,。
定义2.3: 设
是实Banach空间,
,我们说泛函在水平
处满足Cerami条件(简称
条件)是指:如果对任意序列
,当
时,有
,且
,那么
在X中存在收敛的子序列。
引理2.4 [8]:设
成立,则
是
型算子,即对任意给定序列
,若
,且
,则在
中有
。
为了证明主要结果需要使用下列的喷泉定理(见文献 [9] )。
设X为可分自反的Banach空间,存在
,,使得
,,
且
记
,对任意的
,定义
,。
引理2.5: (喷泉定理)设X是可分的自反实Banach空间,
是偶泛函,如果对任意的
,存在
,使得
i)
, ;
ii)
。
iii) 对任意
,I满足
条件;
则I有一列趋于无穷的临界点,即存在序列
,使得
,且
,。
问题(1)对应的能量泛函为
,
。 (3)
在基本假设
和
成立前提下,容易验证(3)是有意义的,且
,。
因此,寻找问题(1)的弱解等价于求
的临界点。
3. 主要结果的证明
引理3.1:设
和
成立,则对任意的
,泛函
满足
条件。
证明:设
序列
,满足
,, (4)
,。 (5)
由(4)、(5)可得
,(6)
。 (7)
首先,证明序列
有界。事实上,如果
无界,则存在子序列(仍记为其本身),使得
,且
,。
令
,,则
且
,,因此,存在子列(仍记为其本身),
(在
中), (8)
(在
中), (9)
。 (10)
我们断言
a.e.
。事实上,令
,假设
,那么,对给定的
,由(6)推得
,。由
可得
,,
且存在
,使得对任意的
,当
时,有
。 (11)
因为
在
上连续,所以存在
,使得对任意的
,有
。 (12)
因此,由(11)、(12)式知,存在
,使得
,。
根据(6)式,有
。
再结合引理2.2和
推得
。
由Fatou引理,可得
,
上式是一个矛盾的结论。故
a.e.
。
因为对任意的
,当
时,
连续,则存在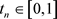 ,使得
,使得
。
由(7)式知,
,。
一方面,取序列
,使得对任意的
,有
,且
,则对任意的
,有
。
根据
和(9)知,
,那么,
。
由于
,所以当n足够大时,有
,即
。
于是结合引理2.2,
。 (13)
令
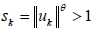 ,,则
。
,,则
。
另一方面,由条件
、
和(4)、(7)式,当n充分大时,有
结合(13)式,有
。
因为
,当
时,从上式可得
,矛盾。故
在
中有界,则存在子列(仍记为其本身),有
(在
中), (14)
(在
中), (15)
。 (16)
取测试函数
代入(7)式中,再结合(14)、(15)式、Hölder不等式和Sobolev嵌入定理,可得
。
于是得到
。 (17)
又
算子满足
型条件。因此,由引理2.4、(14)和(17)式,推得在
中, 。证毕。
。证毕。
引理3.2 若
,则下式成立
。
证明:显然,对任意的
,有
,则当
时,。
令
,使得
,且
。由此,
存在子列(仍记为其本身),使得在
中
,且
,。
由于
是
的闭集,那么对任意的
,,可推得在
中
。又由
 是紧的,则在
中
。故
。证毕。
是紧的,则在
中
。故
。证毕。
引理3.3 在
和
假设下,对任意的
,存在
,使得
i)
, ;
ii)
。
证明:i) 对任意的
,当
时,由引理2.2和
,有
,
其中
。取
,则
。
由引理3.2知,
,又
,因此,
。故
。
证毕。
ii) 根据
,对任意的
,存在
(依赖于M),使得
,。
取
,且
,,则
。
当M充分大时,
。因此,
。于是,存在足够大的
,使得
。
取
,则
。证毕。
定理1.1的证明:首先,由引理3.1和引理3.3知泛函
满足喷泉定理的(i)-(iii)假设;再由
知
为偶泛函。因此,应用喷泉定理,推得在
中临界点序列
满足
,。证毕。
文章引用
王明旻,贾 高. 含Φ-Laplace算子的拟线性椭圆型方程的无穷多解
Infinitely Many Solutions for Quasilinear Elliptic Equations with Φ-Laplacian Operator[J]. 理论数学, 2019, 09(10): 1123-1131. https://doi.org/10.12677/PM.2019.910138
参考文献
- 1. Fukagai, N. and Narukawa, K. (2006) Positive Solutions of Quasilinear Elliptic Equations with Critical Orlicz-Sobolev Nonlinearity on . Funkcialaj Ekvacioj, 49, 235-267.
- 2. Huentutripay, J. and Manasevich, R. (2006) Nonlinear Eigenvalues for a Quasilinear Elliptic System in Orlicz-Sobolev Spaces. Journal of Dynamics and Differential Equations, 18, 901-929. https://doi.org/10.1007/s10884-006-9049-7
- 3. Sunjun, W. (2019) Multiple Solutions for Quasilinear Elliptic Problems with Concave-Convex Nonlinearities in Orlicz-Sobolev Spaces. Boundary Value Problems, 2019, Article Number: 142. https://doi.org/10.1186/s13661-019-1256-3
- 4. Gang, L., Dumitru, M., Haitao, W. and Qihu, Z. (2018) Multiple Solutions with Constant Sign for a -Elliptic System Dirichlet Problem with Product Nonlinear Term. Boundary Value Problems, 67, 1-16.
- 5. Chung, N.T. and Toan, H.Q. (2013) On a Nonlinear and Non-Homogeneous Problem without (A-R) Type Condition in Orlicz-Sobolev Spaces. Applied Mathematics and Computation, 219, 7820-7829. https://doi.org/10.1016/j.amc.2013.02.011
- 6. Ambrosetti, A. and Rabinowitz, P.H. (1973) Dual Variational Methods in Critical Points Theory and Application. Journal of Functional Analysis, 14, 349-381. https://doi.org/10.1016/0022-1236(73)90051-7
- 7. Adams, R. (1975) Sobolev Spaces. Academic Press, New York.
- 8. Carvalho, M.L., Goncalves, V. and Silva, E.D. (2015) On Quasilinear Elliptic Problems without the Ambrosettiı-Rabinowitz Condition. Journal of Mathematical Analysis and Applications, 426, 466-483.
https://doi.org/10.1016/j.jmaa.2015.01.023
- 9. Willem, M. (1996) Minimax Theorems. Birkhäuser, Boston. https://doi.org/10.1007/978-1-4612-4146-1
NOTES
*通讯作者。







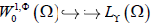 。进一步,有
。进一步,有
 。在条件
下,有连续嵌入:
。在条件
下,有连续嵌入:

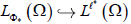 。
。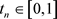 ,使得
,使得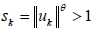 ,,则
。
,,则
。 。证毕。
。证毕。 是紧的,则在
中
。故
。证毕。
是紧的,则在
中
。故
。证毕。