Modern Physics
Vol.05 No.03(2015), Article ID:15232,8
pages
10.12677/MP.2015.53007
The Physical Meaning of the Electron Spin and the Fine Structure Constant
Qingju Tian
Panjiakou Ministry of Water Resources Water Conservancy Bureau, Tianjin
Email: tqj1960@163.com
Received: Apr. 28th, 2015; accepted: May 12th, 2015; published: May 18th, 2015
Copyright © 2015 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
This paper briefly describes the concepts of the quaternion full time D, quaternion momentum G and the quaternion full speed c. Applying these concepts, we study the electronic image, electron spin and the fine-structure constant. Meanwhile, a new calculating formula is derived and more understanding of its physical meaning is given. On the contrary, the scientific nature of the new concept is verified indirectly.
Keywords:Electronic Radius of Classic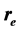 , Compton Wavelength
, Compton Wavelength , Quaternion Momentum
, Quaternion Momentum , The Electronic Image
, The Electronic Image

电子自旋和精细结构常数的物理意义
田清聚
水利部潘家口水利枢纽管理局,天津
Email: tqj1960@163.com
收稿日期:2015年4月28日;录用日期:2015年5月12日;发布日期:2015年5月18日

摘 要
本文简述了四元数全时间 、四元数全动量
、四元数全动量 和四元数全速度
和四元数全速度 等概念,应用这些概念对电子形象、电子自旋、精细结构常数进行了研究,并给出了新的推导计算公式,进而对其物理意义有了更多的理解。反过来也间接验证新概念的科学性。
等概念,应用这些概念对电子形象、电子自旋、精细结构常数进行了研究,并给出了新的推导计算公式,进而对其物理意义有了更多的理解。反过来也间接验证新概念的科学性。
关键词 :电子经典半径 ,电子约化康普顿波长
,电子约化康普顿波长 ,四元数动量
,四元数动量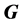 ,电子形象
,电子形象

1. 引言
理论和实验都揭示电子具有内禀运动——自旋,且有与之相联系的自旋磁矩,但是现有理论电子自旋的形象和本质都有些令人费解;再有精细结构常数是物理学中一个重要的无量纲数,怎样从理论上解释它也是当前物理学存在的问题之一。本文以双波包双原点(双弦双原点)微观粒子模型、全时间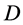 、全动量
、全动量 和微观粒子运动全速度
和微观粒子运动全速度 等一系列新概念[1] 为基础,通过逻辑推理和推导对精细结构常数和电子自旋给出了新的计算路径,从而使其物理意义有了易于理解的一种解释。
等一系列新概念[1] 为基础,通过逻辑推理和推导对精细结构常数和电子自旋给出了新的计算路径,从而使其物理意义有了易于理解的一种解释。
2. 全时间、全动量和全速度概念
我在《微观粒子形象模型假说》一文中引进了微观粒子“四元数”距离 概念和“四元数”能量
概念和“四元数”能量 概念,并进一步推断如果微观物质有双“四维”结构,那么描述微观粒子的四个基本参数能量
概念,并进一步推断如果微观物质有双“四维”结构,那么描述微观粒子的四个基本参数能量 、距离
、距离 、时间
、时间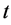 和动量
和动量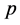 都应有“四元数”结构。因此提出“全时间
都应有“四元数”结构。因此提出“全时间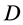 ”和“全动量
”和“全动量 ”新概念并明确了它们之间的关系。为了对精细结构常数和电子自旋讨论的方便有必要回顾一下。
”新概念并明确了它们之间的关系。为了对精细结构常数和电子自旋讨论的方便有必要回顾一下。
2.1. 四元数全时间D的意义
全时间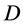 的定义:微观粒子四元数距离
的定义:微观粒子四元数距离 被光速常数
被光速常数 整除等于全时间
整除等于全时间 。它的四元数结构由实部标量
。它的四元数结构由实部标量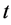 和虚部矢量
和虚部矢量 组成,用公式表示如下
组成,用公式表示如下
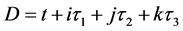 , (1)
, (1)
可见,全时间 的实部标量
的实部标量 就是通常我们熟悉的相对时间变量,而虚部矢量
就是通常我们熟悉的相对时间变量,而虚部矢量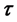 由于其特殊性还不被普遍了解。全时间
由于其特殊性还不被普遍了解。全时间 和四元数距离
和四元数距离 存在如下关系
存在如下关系
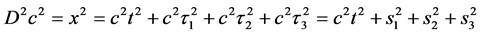 (2)
(2)
2.2. 四元数全动量G的意义
全动量 的定义:微观粒子四元数能量
的定义:微观粒子四元数能量 被光速常数
被光速常数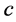 整除等于全动量
整除等于全动量 。它的四元数结构由实部标量
。它的四元数结构由实部标量 和虚部矢量
和虚部矢量 组成,用公式表示如下
组成,用公式表示如下
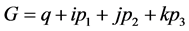 , (3)
, (3)
显然,全动量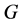 的虚部矢量
的虚部矢量 就是人们熟知的可观测量动量,而实部标量
就是人们熟知的可观测量动量,而实部标量 由于其特殊性还不被熟悉。全动量
由于其特殊性还不被熟悉。全动量 和四元数能量
和四元数能量 存在如下关系
存在如下关系
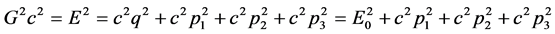 (4)
(4)
2.3. 全时间D和全动量G的关系
四元数全时间 和全动量
和全动量 是全新概念,那么它们之间存在什么关系呢?由经典物理学动量
是全新概念,那么它们之间存在什么关系呢?由经典物理学动量 计算公式
计算公式 得到启示,大胆推断全时间
得到启示,大胆推断全时间 和全动量
和全动量 各分量关系如下:
各分量关系如下:
 , (5)
, (5)
 , (6)
, (6)
 , (7)
, (7)
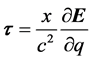 , (8)
, (8)
对于单个微观粒子 与
与 绝对值恒相等;
绝对值恒相等;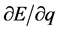 与
与 绝对值恒相等。
绝对值恒相等。
2.4. 定态波函数的传播与全速度概念
人类直观感知的自然界是三维 位形空间世界,若其中任意微观粒子波函数
位形空间世界,若其中任意微观粒子波函数 塌缩在
塌缩在 点出现粒子能量子,四参数
点出现粒子能量子,四参数 、
、 、
、 和
和 有确定值,该状态微观粒子定态平面波函数
有确定值,该状态微观粒子定态平面波函数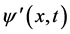 的传播方向与
的传播方向与 方向相同见图1。直线
方向相同见图1。直线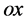 的意义由原点在
的意义由原点在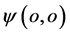 的该微观粒子四维s-t空间方位所决定;若
的该微观粒子四维s-t空间方位所决定;若 与微观粒子四维s-t空间实轴
与微观粒子四维s-t空间实轴 方向重合,观测到的定是光粒子。光粒子全时间
方向重合,观测到的定是光粒子。光粒子全时间 的矢量部分
的矢量部分 为零;若
为零;若 与微观粒子四维s-t 空间某一虚矢
与微观粒子四维s-t 空间某一虚矢 方向相同,观测到的定是静止粒子
方向相同,观测到的定是静止粒子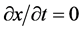 。由于该状态
。由于该状态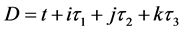 的标量部分
的标量部分 为零(三维
为零(三维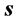 空间任一点的时钟读数都相同),静止粒子平面波前传播速度为
空间任一点的时钟读数都相同),静止粒子平面波前传播速度为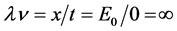 ;一般状态三维
;一般状态三维 空间以
空间以 为自变量的定态波函数
为自变量的定态波函数 传播方向与其动量
传播方向与其动量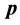 方向相同。其波前传播速度为
方向相同。其波前传播速度为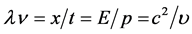 ,其中
,其中 。
。
试想,假如人类不是仅仅能够看到三维 空间世界,而能直接观察四维空间微观粒子的全貌。那么,当波包塌缩粒子出现瞬时,观察者应该能够观察看到
空间世界,而能直接观察四维空间微观粒子的全貌。那么,当波包塌缩粒子出现瞬时,观察者应该能够观察看到 对全时间
对全时间 的全微分
的全微分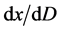 而不仅仅是偏导数
而不仅仅是偏导数 。我们称全微分
。我们称全微分 为微观粒子运动全速度。粒子全速度
为微观粒子运动全速度。粒子全速度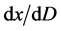 的“模”为光速常量
的“模”为光速常量 。且如下公式
。且如下公式
 (9)
(9)
成立,若将上式中


则关系式
 , (10)
, (10)
成立。当粒子为光子时,
 ,可见,粒子质量
,可见,粒子质量 、全动量
、全动量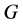 和全速度
和全速度 的关系为
的关系为

Figure 1. Schematic diagram of De Broglie planwave propagation
图1. 德布罗意平面波传播示意图
不难看出,通常在三维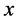 空间观察到的“静止状态”粒子仅是其全速度矢量部分
空间观察到的“静止状态”粒子仅是其全速度矢量部分 为零的状态,为了叙述的方便后面将
为零的状态,为了叙述的方便后面将 状态粒子称作“经典静止”粒子。
状态粒子称作“经典静止”粒子。
同理,单个微观粒子在w-p空间的运动全速度 的“模”也为光速常量
的“模”也为光速常量 ,将全速度
,将全速度 用字母
用字母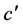 表示如下公式
表示如下公式
 , (11)
, (11)
成立,若将上式中
 ,
,
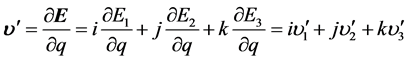
则关系式
 , (12)
, (12)
存在,同样的,粒子参数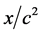 、全时间
、全时间 和w-p空间全速度
和w-p空间全速度 的关系为
的关系为

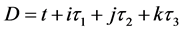 。
。
不难推断,若s-t空间电子出现点参数 ,
, 方向和
方向和 轴的夹角为
轴的夹角为 、w-p空间出现点
、w-p空间出现点 ,
, 和
和 轴的夹角也一定为
轴的夹角也一定为 。
。
3. 电子自旋的意义
3.1. 氢原子结构描述
自然界任何微观粒子都是双波包双原点(双弦双原点)的波–粒二象结构,那么,在此基础上就能够给出氢原子形象进一步的描述:氢原子由一个质子和一个电子组成。通常在三维 空间,质子
空间,质子 “吸收”
“吸收” 区域内的光能量子处于激发状态带正电荷;电子“吸收”
区域内的光能量子处于激发状态带正电荷;电子“吸收” 区域内的光子也处于相应激发状态带负电荷。不难想象低激发态氢原子的形象应该是,在三维
区域内的光子也处于相应激发状态带负电荷。不难想象低激发态氢原子的形象应该是,在三维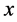 空间电子
空间电子 点的可能出现区域,是以氢原子原心
点的可能出现区域,是以氢原子原心 为原点、半径约为
为原点、半径约为 的三维球面附近区域;因为质子
的三维球面附近区域;因为质子 在三维
在三维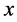 空间的投影很小,所以它的
空间的投影很小,所以它的 出现点就在氢原子原心
出现点就在氢原子原心 附近,氢原子内能量越大质子
附近,氢原子内能量越大质子 越大时质子在氢原子原心附近活动范围也就越大如图2所示。另一方面,在三维
越大时质子在氢原子原心附近活动范围也就越大如图2所示。另一方面,在三维 空间质子
空间质子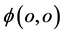 点的可能出现区域是以氢原子另一原心
点的可能出现区域是以氢原子另一原心 为原点、半径约为
为原点、半径约为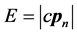 的三维
的三维 球面附近;因为该情况下
球面附近;因为该情况下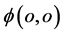 点
点 在三维
在三维 空间投影很小,所以具有了参数
空间投影很小,所以具有了参数 的电子
的电子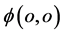 只能在三维
只能在三维 空间氢原子原心
空间氢原子原心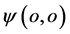 附近出现,氢原子内能越大电子在其原心附近活动范围也就越大。可以想象,氢原子内电子和质子偶合交换作用量子的图景,这一过程在三维
附近出现,氢原子内能越大电子在其原心附近活动范围也就越大。可以想象,氢原子内电子和质子偶合交换作用量子的图景,这一过程在三维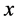 空间看上去近似是电子
空间看上去近似是电子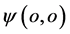 点围绕质子
点围绕质子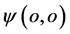 (在原子原心附近出现)旋转;在三维
(在原子原心附近出现)旋转;在三维 空间看上去是质子
空间看上去是质子 点围绕电子旋转。
点围绕电子旋转。
3.2. 电子自旋的推导
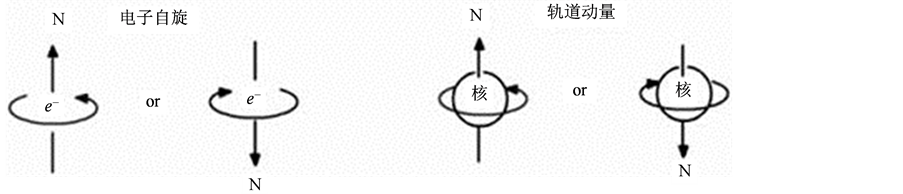
电子有轨道角动量也有自旋角动量。但自旋的本质是什么用已有理论很难诠释,然而物理学家们都肯定了它是一个新的自由度,是与三维空间以外的另一个维度密切相关的物理量。因为自旋的存在决定了不能将电子单纯看成一“几何点”,将其想象为某种意义上的微小“电流环”。比较接近实验结果。因此,我们认定:电子是双四维空间双波包双原点结构的客体,从电子有自旋磁矩考虑它应有小“电流环”的近似结构见示意图3。因为人类在三维 空间不能看到其全貌,所以电子运动的一些方面以内禀运动量子数的形式展现。下面就以经典理论和双波包双原点模型两种思路分别定义电子自旋角动量。
空间不能看到其全貌,所以电子运动的一些方面以内禀运动量子数的形式展现。下面就以经典理论和双波包双原点模型两种思路分别定义电子自旋角动量。
1) 若将电子想象成一不停自转独立的经典三维小“带电球”,那么电子的经典半径[2] 计算如下
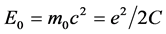 ,电容
,电容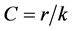 ,
,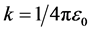
电子的经典半径
 , (13)
, (13)
其中 为电子静止质量,由全动量概念知道,无论电子什么运动状态它的实部标量
为电子静止质量,由全动量概念知道,无论电子什么运动状态它的实部标量 为一恒量,当电子全动量矢量
为一恒量,当电子全动量矢量 为0时,
为0时, ,随着
,随着 的增大
的增大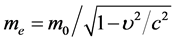 增大,而全速度标量部分
增大,而全速度标量部分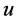 减小但
减小但 不变。一般地人们将做圆周运动的核外电子全动量矢量部分
不变。一般地人们将做圆周运动的核外电子全动量矢量部分 与圆周半径的乘积叫轨道角动量。这里我们将做圆周运动的核外电子全动量标量部分
与圆周半径的乘积叫轨道角动量。这里我们将做圆周运动的核外电子全动量标量部分 与电子的经典半径的乘积
与电子的经典半径的乘积 叫做电子自旋角动量。其表达式
叫做电子自旋角动量。其表达式

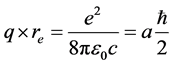
其中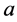 为精细结构常数。考虑
为精细结构常数。考虑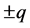 后上式也可表示为
后上式也可表示为
 (14)
(14)
从(14)式可以看出,若电子经典半径 为常数不变,则电子表面速度
为常数不变,则电子表面速度 与电子质量
与电子质量 成反比,当质量
成反比,当质量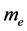 为无穷大
为无穷大 时速度
时速度 为0,当电子质量
为0,当电子质量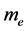 为最小值
为最小值 时速度
时速度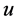 为光速常数
为光速常数 。但这样得出的电子自旋角动量绝对值比
。但这样得出的电子自旋角动量绝对值比 小137倍,显然它与客观实验不符是一个错误的定义。
小137倍,显然它与客观实验不符是一个错误的定义。
2) 正确的途径与定义,应以微观粒子双波包双原点模型和客观实验为基础来建立。试想当电子不

Figure 2. Hydrogen atoms protons and electrons are coupled state diagram
图2. 氢原子质子和电子相互偶合状态示意图
 (a) (b)
(a) (b)
Figure 3. Electron motion state diagram
图3. 电子运动状态示意图
在氢原子核外电磁场中运动完全自由状态时,电子全动量矢量部分 没有轨道角动量,但全动量标量部分
没有轨道角动量,但全动量标量部分 ,本文认为康普顿波长
,本文认为康普顿波长 就是电子自旋的圆周长,约化康普顿波长
就是电子自旋的圆周长,约化康普顿波长 就是自由电子半径。该状态自由电子双波包的两原点
就是自由电子半径。该状态自由电子双波包的两原点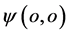 与
与 在三维
在三维 空间的距离为
空间的距离为 。因此,可以定义电子全动量标量部分
。因此,可以定义电子全动量标量部分 与电子的半径
与电子的半径 的乘积的
的乘积的 倍
倍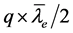 为电子自旋角动量
为电子自旋角动量 。以能量子
。以能量子 出现点为圆心的三维球半径
出现点为圆心的三维球半径
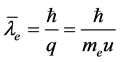 (15)
(15)
考虑到速度 方向恒正交于三维
方向恒正交于三维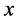 空间所有方向但它有正♁、负⊙的差别,所以,电子自旋角动量
空间所有方向但它有正♁、负⊙的差别,所以,电子自旋角动量 被定义并表示为
被定义并表示为
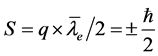 (16)
(16)
仔细分析,电子自旋角动量 在形式上与电子自旋磁矩
在形式上与电子自旋磁矩 很相像。因此我们认为:电子自旋磁矩
很相像。因此我们认为:电子自旋磁矩 在三维
在三维 空间任何方向的投影只能取方向相反大小相等的两个数值。
空间任何方向的投影只能取方向相反大小相等的两个数值。

以 为圆心的三维球面上任一
为圆心的三维球面上任一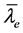 为半径的“电流环”所圈面积的法向都是自旋磁矩
为半径的“电流环”所圈面积的法向都是自旋磁矩 的方向。
的方向。
电子的运动形态如示意图3所示,关于电子速度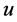 的方向可以这样想象:全速度的标量
的方向可以这样想象:全速度的标量 方向与其三维
方向与其三维 空间全速度矢量部分
空间全速度矢量部分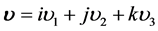 任一方向分量都是垂直正交的,不论分量大、小或为零,所以电子自旋角动量在通常的三维
任一方向分量都是垂直正交的,不论分量大、小或为零,所以电子自旋角动量在通常的三维 位形空间任何方向上投影都应相同。
位形空间任何方向上投影都应相同。
4. 自由电子形象猜想
由上面的讨论可以推断电子在三维 空间的形象:电子有双波包(双弦)双原点结构,三维
空间的形象:电子有双波包(双弦)双原点结构,三维 空间电子自旋项为以
空间电子自旋项为以 为圆心半径为
为圆心半径为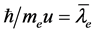 的三维球,
的三维球,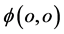 点可能出现在三维球面任一方向
点可能出现在三维球面任一方向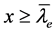 的点上,电子自旋能量子
的点上,电子自旋能量子 出现在三维球原心点
出现在三维球原心点 ,其
,其 方向恒与三维
方向恒与三维 空间任何方向都垂直。经典静止电子
空间任何方向都垂直。经典静止电子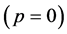 是微观电子运动的特殊状态,该状态电子在能量空间为一根弦,双原点
是微观电子运动的特殊状态,该状态电子在能量空间为一根弦,双原点 和
和 在能量空间距离
在能量空间距离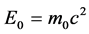 方向不变与轴
方向不变与轴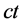 相同,双原点
相同,双原点 和
和 在三维
在三维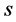 空间的最小距离为
空间的最小距离为 其方向不能确定,
其方向不能确定, 在哪个方位出现决定与其恋爱对象质子的位置,电子总是倾向试图进入与质子组成的家庭。电子全动量标量部分
在哪个方位出现决定与其恋爱对象质子的位置,电子总是倾向试图进入与质子组成的家庭。电子全动量标量部分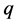 与电子三维球的任何方向半径
与电子三维球的任何方向半径 的乘积的
的乘积的 倍都为该方向电子自旋角动量
倍都为该方向电子自旋角动量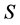 ,在三维
,在三维 空间要测量经典静止电子的位置不可能得到确切结果,因为不管从哪个方向测量并试图接近它都不能突破以
空间要测量经典静止电子的位置不可能得到确切结果,因为不管从哪个方向测量并试图接近它都不能突破以 为圆心半径为
为圆心半径为 的三维球面,而电子能量子出现点
的三维球面,而电子能量子出现点 才是该电子的中心位置。这应该就是微观粒子测不准原理的意义所在。微观实物粒子静止能量也就是其自旋项
才是该电子的中心位置。这应该就是微观粒子测不准原理的意义所在。微观实物粒子静止能量也就是其自旋项 越大三维
越大三维 空间三维球半径就越小反之亦然。
空间三维球半径就越小反之亦然。
5. 精细结构常数的物理意义
精细结构常数是物理学中一个重要的无量纲数,常用希腊字母 表示。氢原子中精细结构常数表示三维
表示。氢原子中精细结构常数表示三维 空间电子运动速度
空间电子运动速度 和光速
和光速 的比值,计算公式为
的比值,计算公式为
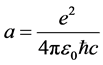
其中 是电子的电荷,
是电子的电荷,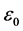 是真空介电常数,
是真空介电常数, 是约化普朗克常数,
是约化普朗克常数, 是真空中的光速。从表面看来,精细结构常数
是真空中的光速。从表面看来,精细结构常数 只不过是另外一些物理常数的简单组合。然而,量子理论以后的发展表明,
只不过是另外一些物理常数的简单组合。然而,量子理论以后的发展表明, 具有深刻的物理意义。
具有深刻的物理意义。
假若有一电子几率波函数塌缩,氢原子三维 空间原心点
空间原心点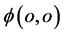 相对于四维s-t空间坐标系原点电子能量子出现
相对于四维s-t空间坐标系原点电子能量子出现 点时间参数
点时间参数 是“负”值如图4所示,就可以说图4所示电子带“负”电荷显“阴”性。“阴”性粒子
是“负”值如图4所示,就可以说图4所示电子带“负”电荷显“阴”性。“阴”性粒子 只能在四维s-t空间“负”
只能在四维s-t空间“负”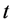 空间范围内出现。它“吸收”“负”
空间范围内出现。它“吸收”“负” 空间内的
空间内的 其
其 绝对值增大;它的
绝对值增大;它的 绝对值减小或
绝对值减小或 绝对值增大时
绝对值增大时 失去能量“发射”光子
失去能量“发射”光子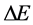 在s-t空间传播。
在s-t空间传播。
看图4若观察者站在氢原子原心 处观察到电子能量子出现在
处观察到电子能量子出现在 点,由狭义相对论知道电子一定具有了能量
点,由狭义相对论知道电子一定具有了能量 和动量
和动量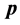 。在这一点电子的全速度
。在这一点电子的全速度 。且如下公式
。且如下公式
 ;
; ;
;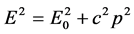
 ;
; 成立。现在要问,为什么电子会有玻尔半径
成立。现在要问,为什么电子会有玻尔半径 这一固定值,它肯定有其深刻的物理原因。想象一下在氢原子内经典静止电子
这一固定值,它肯定有其深刻的物理原因。想象一下在氢原子内经典静止电子 的运动状态,其一,经典静止电子(
的运动状态,其一,经典静止电子( ;
; )它的德布罗意波长
)它的德布罗意波长 为
为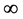 ,因此若没有其它外力作用电子仅仅能够出现在距离原子核无穷远处。其二,在电磁场的作
,因此若没有其它外力作用电子仅仅能够出现在距离原子核无穷远处。其二,在电磁场的作
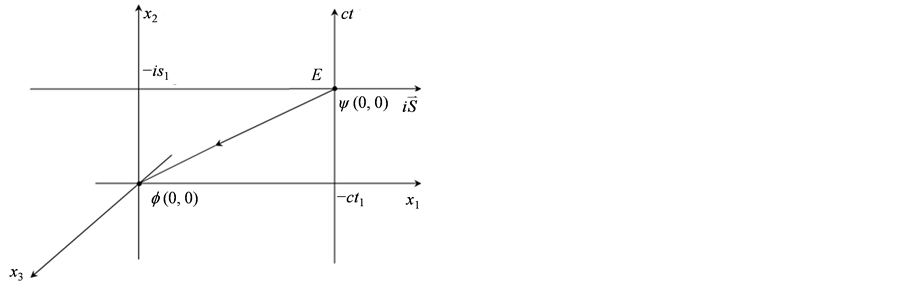
Figure 4. Negatively charged electrons 3D x space diagram
图4. 负电荷电子三维x空间出现示意图
用下电子被核吸引 不断增大,
不断增大, 随之减小,出现点由远而近向原子核靠近。按玻尔假定,当电场引力与绕核转动形成的离心力相等时,电子受力平衡保持匀速圆周运动氢原子能量最低,玻尔轨道半径可表示为
随之减小,出现点由远而近向原子核靠近。按玻尔假定,当电场引力与绕核转动形成的离心力相等时,电子受力平衡保持匀速圆周运动氢原子能量最低,玻尔轨道半径可表示为
 。
。
试想,自由电子经典静止时( ;
; ),三维
),三维 空间电子双原点
空间电子双原点 和
和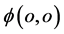 的最小距离为电子约化康普顿波长——电子半径,本文以为:三维
的最小距离为电子约化康普顿波长——电子半径,本文以为:三维 空间
空间 不变
不变 增加电子吸收光子能量增加时,其双原点
增加电子吸收光子能量增加时,其双原点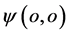 和
和 的距离增大,
的距离增大, 不变
不变 减小电子也吸收光子能量增加,其双原点
减小电子也吸收光子能量增加,其双原点 和
和 的距离由远及近而减小。因此,我们认为图4所示氢原子核所在点
的距离由远及近而减小。因此,我们认为图4所示氢原子核所在点 的运动可以沿着
的运动可以沿着 为常数的直线由远方与电子
为常数的直线由远方与电子 加速靠近。显然,由于电子半径
加速靠近。显然,由于电子半径 的存在,基于电子能量子
的存在,基于电子能量子 时间
时间 ,时间轴绝对值小于
,时间轴绝对值小于 的区域电子另一原点
的区域电子另一原点 是不能出现的。与此同时,可以想象在能量空间氢原子运动的同一过程会是怎样的一种情景呢?由狭义相对论和大对称原则我们认为:比照三维
是不能出现的。与此同时,可以想象在能量空间氢原子运动的同一过程会是怎样的一种情景呢?由狭义相对论和大对称原则我们认为:比照三维 空间电子运动能量参数
空间电子运动能量参数 关系,对称的一定有三维能量空间里关于长度参数
关系,对称的一定有三维能量空间里关于长度参数 的关系式
的关系式
 (17)
(17)
存在,再考虑能量空间电子运动全速度 ;
; 。由三角函数关系
。由三角函数关系 ,所以有
,所以有 。进而
。进而
 。
。
又由于,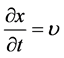 与
与 绝对值恒相等;
绝对值恒相等; 与
与 绝对值恒相等,
绝对值恒相等, 。
。
所以(17)式又可变为
 , (18)
, (18)
显然,玻尔半径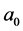 的大小由三维
的大小由三维 空间原子内电子的速度
空间原子内电子的速度 的大小决定。我们知道在氢原子内玻尔半径上关系式
的大小决定。我们知道在氢原子内玻尔半径上关系式
 (19)
(19)
成立, 就是精细结构常数。
就是精细结构常数。
6. 结语
本文能对电子形象、自旋和精细结构常数从新的角度给出一个物理解释,是运用双波包双原点(双弦双原点)微观粒子模型、动量四元数 、时间四元数
、时间四元数 和全速度四元数
和全速度四元数 等新概念,对物理事实重新审视的自然结果,不论该结果能否经受住理论与实践的检验,它都从一个侧面证明了建立新概念对于物理学发展的重要性,也说明了在解决现代物理学困扰的努力中,基于哲学思辨的经典观点依然有重要借鉴价值。
等新概念,对物理事实重新审视的自然结果,不论该结果能否经受住理论与实践的检验,它都从一个侧面证明了建立新概念对于物理学发展的重要性,也说明了在解决现代物理学困扰的努力中,基于哲学思辨的经典观点依然有重要借鉴价值。
文章引用
田清聚, (2015) 电子自旋和精细结构常数的物理意义
The Physical Meaning of the Electron Spin and the Fine Structure Constant. 现代物理,03,48-56. doi: 10.12677/MP.2015.53007
参考文献 (References)