ABSTRACT

Whether the rest mass of photon is zero is one of the fundamental problems in physics. Einstein used Planck’s constant h as a constant of the photon energy, indicating that the photon is no rest mass. In this paper, the analysis and research results of the absorption spectroscopy, Planck’s blackbody radiation equation, Einstein’s photoelectric effect theory and experiment show that Planck’s constant h is not the energy constant of the photon but rather the energy constant of the nucleus outside orbit electrons or metal conduction band free electrons. A constant h_m of photons rest mass is assumed. It is more reasonable that the photon rest mass constant and Planck’s constant are used to explain the absorption spectra, blackbody radiation and the photoelectric effect, and other related physical experiment. The argument about Planck’s constant h and constant h_m of photons rest mass put forward new ideas for the development of relevant theoretical and experimental physics.

Keywords:Photons Rest Mass Constant, Planck’s Constant, Absorption Spectrum, Blackbody Radiation, Photoelectric Effect

普朗克常数与光子静止质量常数统一实验分析

吴先金

长江大学信息与数学学院，湖北 荆州

收稿日期：2016年11月3日；录用日期：2016年11月19日；发布日期：2016年11月22日

摘 要

光子有没有静止质量是物理学的一个基本问题。爱因斯坦将普朗克常数h作为光子的能量常数，表明光子没有静止质量。本文对吸收光谱、普朗克黑体辐射公式和爱因斯坦光电效应理论与实验进行分析研究，结果表明普朗克常数h不是光子的能量常数，而是原子核外轨道电子或金属导带自由电子的能量常数，并提出了光子静止质量常数h_m假设。以光子静止质量常数和普朗克常数同时解释吸收光谱、黑体辐射和光电效应以及其他相关物理实验更具有合理性。本文对普朗克常数h与光子静止质量常数h_m的论证，为物理学相关理论与实验的发展提出了新的思路。

关键词 :光子静止质量常数，普朗克常数，吸收光谱，黑体辐射，光电效应

1. 引言

光子有没有静止质量是物理学的一个基本问题。研究光子的静止质量及其静止质量常数，对于物理学理论的发展具有极其重要的意义，对于物理学实验与应用的发展具有极其重要的价值。

19世纪Maxwell创立电磁理论，1900年普朗克提出h常数假设，1905年爱因斯坦建立光量子理论、光电效应理论和狭义相对论，对物理学特别是量子物理学的发展起到了巨大的作用。但是，上述理论的一个前提条件是，光子的静止质量必须为零。

随着物理学的发展，光子是否具有静止质量的问题，曾引起很多物理学家的关注。1930年，Proca A [1] 用重电磁场理论研究光子的非零静止质量问题。1940年，德布罗意(de Broglie) [2] 提出用测量双星发射不同频率的光波到达地球的时间之差来确立光子静止质量的方法，给出光子静止质量的上限值为0.8 × 10⁻³⁹ g。1943年，薛定谔(Schrödinger) [3] 提出用更大尺度的磁场确立光子静止质量，他用地磁数据给出光子静止质量的上限值为2 × 10⁻⁴⁷ g。2006年，涂良成 [4] 通过扭秤实验，给出光子静止质量的上限为1.5 × 10⁻⁵² g。许多物理学家运用Proca重电磁方程、Coulomb反平方定律实验、Ampère环路定律实验、“Schrödinger外来场”方法、星际磁流体力学方法、引力偏折方法，以及扭称实验等，对光子的静止质量进行检验，给出了一系列光子静止质量上限。2010年，Alfred Scharff Goldhaber和Michael Martin Nieto [5] 对光子静止质量实验和数据进行了综述。2014年国际粒子数据组 [6] 介绍了一组光子静止质量上限的数据，并推荐光子静止质量值小于1 × 10⁻¹⁸ eV，约等于1.783 × 10⁻⁵¹ g。到目前为止，人们通过相关实验寻找光子静止质量上限，但没有深入研究光子的静止质量与波长之间的关系。

本文基于对吸收光谱、普朗克黑体辐射公式和爱因斯坦光电效应理论与实验进行分析研究，发现普朗克常数h不是光子的能量常数，而是原子核外轨道电子或金属导带自由电子的能量常数，并提出了光子(或基本粒子)静止质量常数h_m假设，主要研究光子、电子的静止质量及其静止质量与波长的关系，研究光子与电子之间的相互作用。运用光子静止质量常数可以更加科学、精确地分析各种相关物理实验和物理现象，从而促进物理学理论与实验的发展。下面主要通过“吸收光谱”、黑体辐射和光电效应实验对光子静止质量常数予以解释和检验。

2. 光子静止质量常数假设

1905年，Einstein [7] 研究认为，如果用光的能量在空间中不是连续分布在越来越大的空间之中，而是由个数有限的、局限在空间各点的能量子所组成，这些能量子能够运动，但不能再分割，而只能整个地被吸收和产生出来。

光子、电子等基本粒子具有同样的物理属性，即“波粒二象性”。基本粒子的粒子属性反映其静止属性(静止是相对的)，波动属性反映其运动属性(运动是绝对的)。光子与电子一样，具有静止质量。1897年汤姆森实验 [8] 证明电子有质量和电荷。1923年康普顿实验 [9] 证明电子有波长，建立了下列公式：

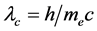(1)

式中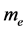，为电子质量，单位是kg；为康普顿波长，单位是m；c为光速，单位是m/s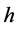；为普朗克常数，单位是J∙s。

如果将基本粒子看作是一个球体粒子，这个粒子的静止质量与其波长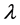倒数的三次方成正比，波长越长，质量越小，波长越短，质量越大。因此，可以建立光子(或基本粒子)静止质量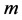的公式：

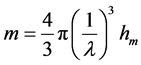(2)

式中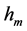，为光子静止质量常数，单位是kg∙m³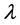，是光子(或基本粒子)的波长。电子质量、电子波长这两个常数通过实验反复证明是非常精确的，因此，可以用来计算光子静止质量常数。2012年国际粒子数据组 [10] 推荐，电子质量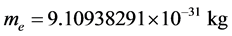，电子康普顿波长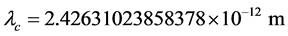，则：

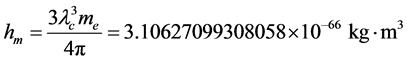(3)

这样，可以用式(2)计算各种基本粒子包括不同波长光子的静止质量。1905年，爱因斯坦 [7] 认为，光子的能量E等于普朗克常数h乘以光子的频率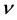；同时，爱因斯坦 [11] 推导出物体的质能方程E = mc²及

运动物体的质能方程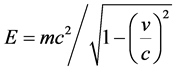，E为物体的能量，m为物体的质量，c为光速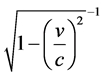，为

计算基本粒子运动质量的狭义相对论洛伦兹因子，单位是m/s，ν为物体运动速度。这里，可以将光子、电子以及其他基本粒子的能量E计算公式统一起来：

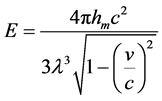(4)

光子(或基本粒子)静止质量常数的物理意义在于：运用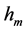可以计算不同波长光子和各种基本粒子的静止质量和能量。

3. 基于h与h_m的吸收光谱原理

1802年，伍朗斯顿(W. H. Wollaston) [12] 就发现太阳光谱中的若干暗线。1814年德国物理学家弗劳恩霍夫(Joseph von Fraunhofer) [13] 再次观察到太阳光谱中的暗线，开始系统研究和仔细测量这些暗线的波长。1859年，基尔霍夫和本生 [14] [15] 注意到几个弗劳恩霍夫线与加热元素的光谱中的发射线重合 [16] ，并推断这些暗线是由于太阳辐射的连续光谱被太阳表面大气中的元素吸收相应波长的光线而产生的 [17] 。1955年，澳大利亚科学家瓦尔西(A. Walsh) [18] 、荷兰学者阿肯麦德(C. T. J. Alkemade)和米拉芝(J. M. W. Milatz) [19] 分别独立地发表了原子吸收光谱分析方法的论文，开创了火焰原子吸收光谱法。

毫无疑问，原子吸收光谱实验是科学的。但“吸收光谱”被解释为：当辐射通过原子蒸汽，且辐射频率相应于原子中的电子由基态跃迁到较高能态所需要能量的频率时，原子从入射辐射中吸收能量，发生共振吸收，产生原子吸收光谱 [20] [21] 。原子的基态电子吸收光子跃迁到激发态，激发态电子由高能态回到基态时发射同样波长光子，而发射的光子向不同方向而去，因此，经过原子气体的光谱呈现出许多暗线。

在这里，“吸收光谱”应解释为入射光子与原子核外电子的“弹性碰撞散射光谱”。当入射光子进入原子时，不同波长的光子入射深度是不同的，波长短的光子入射较深，波长长的光子入射较浅。当光子入射到可发射相同波长光子的电子轨道时，立即被该轨道电子弹性碰撞散射，而散射的光子向不同方向而去。与发射光子一样，被弹性碰撞散射的光子也获得同样的速度而离开原子。人们看到自然界非自身发光的各种元素、各种物体，在日光或白光照射下都呈现自身的颜色，组成这些颜色的光谱应是轨道电子的弹性碰撞散射光谱，而不是轨道电子的发射光谱。

电子跃迁轨道(能级)、发射光子都需要做功，消耗能量，因此，入射光子的能量远远大于发射光子的能量。

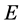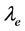原子核外电子在轨道上运行(或自由电子在金属导带上运行)具有一定的能量、波长、频率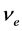，普朗克常数正是计算轨道电子(或金属导带自由电子)能量的常数：

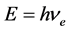(5)

与轨道电子发生弹性碰撞散射的光子的能量远远小于轨道电子的能量。与轨道电子发生弹性碰撞吸收的光子(下面简称吸收光子)的能量等于轨道电子的能量。只有两者能量相等，才能发生弹性碰撞吸收。如紫外线入射至金属，不是与发射紫外线的轨道电子发生弹性碰撞吸收，而是与能量相等的金属导带自由电子发生弹性碰撞吸收，使电子跃迁到金属表面。原子轨道电子或金属导带自由电子的能量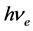用下式表示：

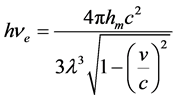(6)

式中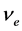，为轨道电子或辐射光子频率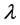，为入射光子波长。与轨道电子(自由电子)发生弹性碰撞吸收的光子的波长远远大于该轨道电子散射(或辐射)光子的波长。吸收光子波长与发射光子波长用下式计算：

(7)

式中，计算吸收光子波长时，为发生弹性碰撞吸收(或基态)的电子能量；计算散射(或辐射)光子波长时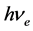，为发生弹性碰撞散射(或激发态)的电子能量。因此，辐射光子波长与辐射该光子的轨道电子波长相等，散射光子波长峰值与散射该光子的轨道电子波长相等。

4. 基于h_m的黑体辐射公式与基于h的黑体辐射公式一致性论证

1900年，马克斯﹒普朗克 [22] 在研究物体热辐射时，运用内插法，推导出黑体辐射的两个公式：

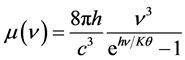(8)

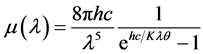(9)

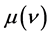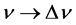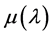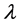式中为辐射黑体单位体积光子频率间隔的能量密度，单位是W∙s²/m³；为式(8)右边乘以黑体辐射的能量密度，单位是W∙s/m⁴；为光子波长，为光子的频率，单位是Hz，K为波尔兹曼常数，单位是J/K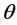，为绝对温度，单位是K。

普朗克将能量元素解释为一个能量单元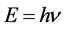。在这里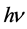，实际上为原子轨道电子或金属导带自由电子的能量。如果将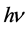作为一个能量单元，那么这个能量单元是由相应轨道电子发射的一定数量的光子组成的。基于这样的解释，普朗克黑体辐射公式是更加合理的。

1906年，爱因斯坦 [23] 认为，普朗克先生在他的黑体辐射理论中给物理学引进了一个新的假说性元素，即光量子假说，并将能量元素定义为光量子。这样就将光子的能量与轨道电子能量等同起来，并奠定了光子静止质量为零的理论基础。

在特定温度的辐射黑体中，不同波长的光子具有不同的动质量，它们各自占有一定的空间。某一特定空间，如果被波长短的光子占有，能量就大，如果被波长长的光子占有，能量就小。因此，对普朗克黑体辐射公式可以进行重新思考和修正，以光子静止质量常数假设为基础，给出一个新的黑体辐射公式。毋用置疑，普朗克黑体辐射公式与黑体辐射实验数据吻合得很好，新的黑体辐射公式计算的结果应与普朗克黑体辐射公式计算的结果应是完全一致的。新的黑体辐射公式的原理是，在单位时间、单位面积的黑体辐射中，每一波段(或频率段)辐射的能量等于该波段(或频率段)辐射光子的动质量乘以光速c的平方再乘以每秒辐射光子数，即用式(4)右边乘以每秒辐射光子数：

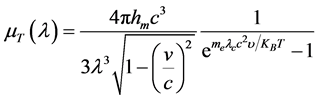(10)

式中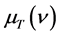：为黑体单位面积以频率间隔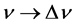每秒辐射某一频率光子的能量，单位是Wm²/s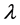；为相应光子的波长，或辐射该光子的轨道电子的波长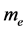，为电子质量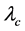，为电子的康普顿波长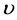，为相应辐射光子的波数，或辐射该光子的轨道电子的波数，单位是/m，K_B为波尔兹曼常数，单位是J/K，T为黑体绝对温度，单位是K。

将式(10)右边乘以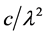，得到下列黑体辐射公式：

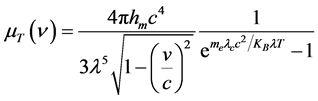(11)

式中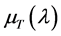为式(10)右边乘以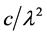黑体辐射某一波长光子能量，单位是W∙m/s²。在式(8)、(9)、(10)、(11)中，e的指数项是相等的：

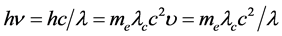(12)

原子核外轨道电子能量等于电子的质量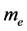乘以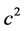再乘以电子的康普顿波长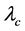与相应辐射光子波长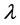(或电子在该轨道上的波长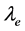)的比值。这样，进一步证明了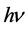为原子核外轨道电子或金属导带自由电子的能量。将式(8)中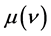代替式(10)的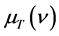，可以推导出下式，计算光子的运行速度：

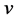(13)

式(8)中普朗克常数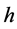为6.626069574 × 10⁻³⁴ J∙s，式(8)和式(13)中，K、K_B为1.3806488 × 10⁻²³ J/K，θ、T为绝对温度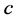，为2.99792458 × 10⁸ m/s [10] ，为3.14159265358979，计算得v = 299,792,457.9999999335677253410648 m/s。从式(10)可以推导出下式，进一步论证并计算光子静止质量常数：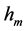

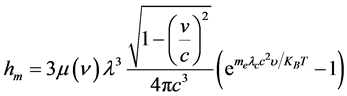(14)

在这里，将普朗克黑体辐射公式的计算结果与新的黑体辐射公式的计算结果进行比较，以检验两者的一致性。设太阳表面温度为6000 K，向空间不断辐射各种不同波长的光子，用式(8)与式(10)分别计算7种可见光子辐射能量密度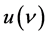、辐射能量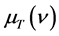，并用式(10)计算光子的质量m和能量E。计算结果见表1。

两式计算结果是完全一致的。将式(9)与式(11)的计算结果进行比较，也是完全一致的。这样，光子静止质量常数不仅可以用来计算黑体辐射，而且可以更深刻地揭示黑体辐射的物理机制。

5. 光电效应实验对h与h_m的检验

1905年，爱因斯坦 [7] 在论述光电效应原理时曾指出，“最简单的设想是，一个光量子把它的能量全部给予了单个电子：我们要假设这就是实际上发生的情况。可是这不应当排除，电子只从光量子那里接受了部分能量。一个物体内部具有动能的电子当它到达物体表面时已经失去了它的一部分动能。此外，还必须假设，每个电子在离开物体时还必须为它脱离物体做一定量的功P”。1906年，爱因斯坦 [23] 进一步论述了光电效应原理，认为频率为的光只能够吸收和发射能量为的量子，这里R是应用于克分子的气体方程的绝对常数，N是克分子中的实际分子数，β是维恩(以及普朗克)辐射公式中指数系数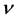，是有关的光的频率。一个电子(电荷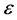)要从金属运动到气体中，必须至少带有电势V乘以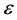的能量。光量子能量一经超过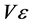，一部分吸收光的电子就会离开金属。一种金属的正电序愈大，在该金属中引起光电效应的最低光子频率就愈小。并提出了著名的光电效应方程：

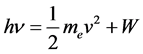(15)

式中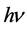，为入射光子的能量，为电子离开金属表面后的动能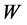，为电子的金属逸出功，即电子从导带基态跃迁到金属表面并脱离金属表面所做的功。

表1. 式(8)与式(10)计算结果比较

爱因斯坦的光子理论、光电效应理论是科学的，但是，有些地方需要进行修正。一是应将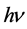作为金属导带相应能级(与电子轨道能级类似)自由电子的能量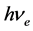，不应作为入射光子能量；二是应在光电效应方程中考虑金属导带相应能级自由电子的能量。入射光子与电子发生弹性碰撞吸收之后，将全部能量传递给了电子，此时电子的能量应是两者之和，即电子所在能级的能量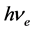与以光子(或基本粒子)的静止质量常数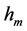计算的相应波长入射光子的能量之和。因此，应将光电效应方程修正为：

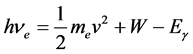(16)

式中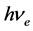，为金属中相应能级自由电子的能量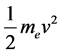，为电子离开金属表面后的动能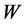，为电子的金属逸出功，为入射光子能量。

1916年，密立根 [24] 通过实验检验了爱因斯坦的光电效应方程，并对普朗克常数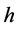进行了测定。密立根的实验是科学的，如果按式(16)计算实验数据，得到的结论会更接近物理真实。

5.1. 原子核外电子轨道能级和自由电子金属导带能级可以用电压表示

原子核外电子轨道能级与电子轨道绕核半径呈反比，半径越小，能级越大，半径越大，能级越小。这个能级可以用电压表示，半径越小，电压越大，半径越大，电压越小。同理，自由电子金属导带能级与离核半径也呈反比，也可以用电压表示。原子核外电子轨道能级，一是可以由其吸收光子的波长确定其基态轨道能级；二是可以由其辐射光子的波长确定其激发态轨道能级。自由电子所在金属导带能级，一是可以由其吸收光子的波长确定其导带基态能级；二是可以直接测量其截止电压确定其导带基态能级。用式(6)计算轨道电子能量(金属导带电子能量)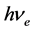。轨道电子(金属导带电子)波长用式(7)计算。用下式计算其电压(能级)：

(17)

式中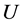，为轨道电子(金属导带电子)电压，为轨道电子(金属导带电子)波长，为维恩常量，取值2.8977721 × 10⁻³ mk [10] ，0.10204 (kg∙m/J)为电子的能量单位由公斤转换为焦耳的比例。电压与温度一样，与波长呈反比。目前，人们做光电效应实验，入射光子波长分别取值365 nm、404.7 nm、435.8 nm、456.1 nm和577 nm。由式(6)、(7)计算得到以上入射光子对应的金属导带基态电子波长为1.73892215031818 × 10⁻⁴ m、2.37028822658046 × 10⁻⁴ m、2.95980584781282 × 10⁻⁴ m、5.8239558733381 × 10⁻⁴ m、6.86956102094362 × 10⁻⁴ m，由式(17)计算得到对应导带基态电子电压为1.70041347181584 V、1.24747978650082 V、0.999013720114453 V、0.507711032697988 V、0.430433129835396 V。这组导带基态电子电压可作为上述入射光子截止电压的理论值。高质量光电管测出的截止电压应接近于这组理论值。

以普朗克常数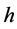计算的上述光电效应入射光子能量远远大于处于截止电压的金属导带基态电子能量。以光子静止质量常数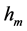计算的入射光子能量等于截止电压的金属导带基态电子能量，由式(6)计算分别为1.14234307965138 × 10⁻²¹ J、8.38060815639394 × 10⁻²² J、6.71140536443083 × 10⁻²² J、3.41081857017901 × 10⁻²² J、2.89166320586175 × 10⁻²² J。

5.2. 电子的金属逸出功计算

金属导带基态电子吸收入射光子，获得更大动能，电子就会跃迁到金属表面。跃迁到金属表面电子，也具有一定能级(这个能级与金属材料特性有关)。导带基态电子能级与金属表面电子能级差为电子跃迁时所做的功，电子脱离金属表面到光电管的真空中也需要做功，两者之和为电子的金属逸出功。电子的金属逸出功大小与光电管的真空度有关。如果光电管具有绝对真空度，这个能级所对应的温度也应该大于−273.15℃。如果以−273.15℃为极限值，与这一温度相对应的波长为7.91526449 × 10⁻¹ m，电压值为3.73567636883856 × 10⁻⁴ V。用式(5)计算得到电子在绝对零度能级上的能量为2.50963904867375 × 10⁻²⁵ J。电子金属逸出功为截止电压导带基态电子能量减除与−273.15℃相应能级电子的能量。因此，上述光电效应实验入射光子波长所对应的截止电压的电子金属逸出功分别为1.14209211574651 × 10⁻²¹ J、8.37809851734527 × 10⁻²² J、6.70889572538216 × 10⁻²² J、3.40830893113034 × 10⁻²² J、2.88915356681308 × 10⁻²² J。

5.3. 光电效应实验能够精确测定电子的电荷

脱离金属表面的电子可以被检测，截止电压也可以被测定。处于截止电压的电子的能量正是该电子在这一金属导带基态的电荷。光电效应实验可以精确测定电子的电荷。以1伏特电压计算，一个电子的电荷的理论值为6.71803122349705 × 10⁻²² (c or J/v)。因此，用下列公式可以计算原子核外轨道电子的能量或金属导带基态自由电子的能量：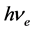

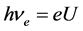(18)

式中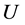，为轨道电子或自由电子电压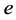，为电子电荷。如果用现有电子电荷常数值1.602176565 × 10⁻¹⁹ (C) [10] 和式(18)计算，辐射巴耳默线系最短光子波长365 nm对应的轨道电子电压只有3.39682720533941 V。也就是说，紫外线足以使该轨道上的电子跃迁到金属表面，这显然不符合事实。将6.71803122349705 × 10⁻²² (J/V)作为新的电子电荷常数，计算365 nm波长光子对应的轨道电子电压为810.105931736986 v。普朗克常数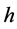也可由下式计算：

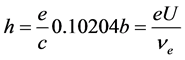(19)

这一等式进一步证明普朗克常数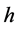是原子核外轨道电子或金属导带自由电子的能量常数。

5.4. 金属导带基态电子逸出最大初始动能计算

电子从导带基态能级跃迁到金属表面能级，再脱离金属表面，几乎消耗了入射光子的全部能量。电子逸出最大初始动能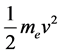用下式表示：

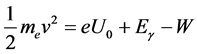(20)

电子逸出最大初始动能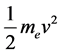略大于入射光子能量，或者略大于导带基态电子的能量，因为电子没

有逸出到绝对真空。以绝对零度为极限，用式(20)计算上述光电效应实验入射光子对应的电子逸出最大初始动能，分别为1.14259411044238 × 10⁻²¹ J、8.38311846430394 × 10⁻²² J、6.71391567234083 × 10⁻²² J、3.41332887808901 × 10⁻²² J、2.89417351377175 × 10⁻²² J。

5.5. 光电效应测定普朗克常数和光子静止质量常数

用上述入射光子对应的截止电压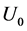理论值与导带基态电子频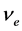率计算斜率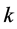，再乘以电子电荷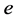，得到普朗克常数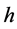。计算结果见表2。斜率用最小二乘法公式计算：

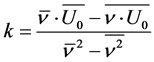(21)

表2. 导带基态电子频率与截止电压的关系

设电荷e = 6.71803122349705 × 10⁻²² (J/V)，计算结果：k = 9.86311220290939 × 10⁻¹³，h = 6.626069574 × 10⁻³⁴ J∙s。

用上述入射光子对应的导带基态电子频率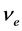与电子能量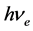(或入射光子能量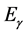)计算斜率。该斜率就是普朗克常数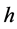，而且直线上任意两点的斜率都相等。计算结果见表3。

计算结果：k = 6.626069574 × 10⁻³⁴。

光电效应也可以测定光子静止质量常数。上述截止电压理论值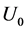与入射光子的能量密度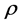这两组数据计算斜率，再乘以电子电荷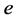，得到光子静止质量常数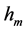，计算结果见表4。用下列公式计算入射光子的能量密度：

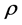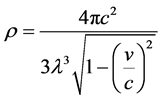(22)

设电荷e = 6.71803122349705 × 10⁻²² (J/V)，计算结果：k = 4.62378171482154 × 10⁻⁴⁵，h_m = 3.10627099308058 × 10⁻⁶⁶ kg∙m³。

5.6. 基于实验数据的两种普朗克常数h计算方法比较

1916年，密立根 [23] 以入射光子的频率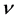与相应的截止电压两组数据计算斜率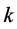，再乘以电子电荷e，(如电子电荷常数值为1.602176565 × 10⁻¹⁹ C)，得到普朗克常数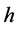。这种计算方法一直沿用到现在。第二种是本文提出的新的计算方法，即以导带基态电子频率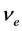与相应的截止电压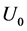两组数据计算斜率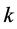，再乘以电子电荷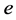，得到普朗克常数。在这里，电子电荷常数为6.71803122349705 × 10⁻²² (J/V)。

下面以作者在长江大学物理实验室三台光电效应仪器上获得的实验数据进行上述两种普朗克常数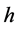计算方法的比较分析。实验仪器为中国南京激光仪器厂生产的“GD−Ⅱ型光电效应实验仪”。实验参数，光源与光阑孔距离L为40 cm，光阑孔Φ为5 mm，电流单位I为10⁻¹³ A。采用零电流法，测验截止电压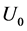与相应入射光子频率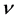或导带基态电子频率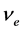之间的关系，获取实验数据。相关实验数据与计算结果见表5。

式中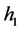，为密立根方法计算数据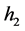，为新方法计算数据。以实验数据计算结果表明，新的计算方法所得的数据更接近普朗克常数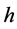。以截止电压理论值计算普朗克常数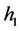，为6.574961 × 10⁻³⁴ J∙s，与密立根计算所得的值6.56 × 10⁻³⁴ J∙s基本吻合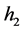；为6.626069574 × 10⁻³⁴ J∙s，与国际粒子数据组的推荐值相吻合。因此，这些实验数据进一步检验了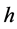是原子核外轨道电子或金属导带自由电子的能量常数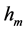，是光子静止质量常数。

6. 结论

本文基于对吸收光谱、黑体辐射和光电效应的原理与实验的研究，论证了普朗克常数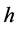不是光子的能量常数，而是原子核外轨道电子或金属导带自由电子的能量常数，同时论证了光子静止质量常数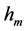的合理性。这两个常数在上述每一实验中，能够同时予以检验和证明。本文对“吸收光谱”进行新的解释，

表3. 导带基态电子频率与能量的关系

表4. 截止电压与入射光子的能量密度的关系

表5. 基于实验数据的两种普朗克常数h计算方法比较

认为“吸收光谱”是“弹性碰撞散射光谱”，当入射光子能量等于轨道电子(或自由电子)能量时，“发生弹性碰撞吸收”，当入射光子波长等于轨道电子(或自由电子)波长时，“发生弹性碰撞散射”。以光子静止质量常数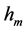建立新的黑体辐射公式，论证了两种黑体辐射公式计算结果的一致性。以光电效应实验数据检验了普朗克常数和光子静止质量常数。本文提出光子(或基本粒子)静止质量常数假设，对普朗克常数假设进行新的解释，为物理学相关理论与实验的发展以及相关学科的发展提出了新的思路。

文章引用

吴先金. 普朗克常数与光子静止质量常数统一实验分析
Unified Experimental Analysis of Planck Constant and Photons Rest Mass Constant[J]. 现代物理, 2016, 06(06): 183-193. http://dx.doi.org/10.12677/MP.2016.66018

参考文献 (References)