Modern Physics
Vol.
09
No.
01
(
2019
), Article ID:
28328
,
7
pages
10.12677/MP.2019.91002
Classification of Quasi-Einstein Metric
Jinnan Li, Xiang Gao*
School of Mathematical Sciences, Ocean University of China, Qingdao Shandong

Received: Dec. 12th, 2018; accepted: Dec. 27th, 2018; published: Jan. 2nd, 2019

ABSTRACT
The natural extension of Einstein's metrics for quasi-Einstein metrics (also known as Ricci soliton) has important applications in gauge field theory and super-string theory. There are two important aspects of it: One looking at the influence on the geometry and topology by the quasi-Einstein metric structure of the Riemannian manifold; and the other looking at its geometric properties and invariant. In this paper, we are interested in summarizing the classification of it and giving some results about gradient steady and expanding quasi-Einstein metric under the assumption of curvature, Weyl tensor and Bach flat.
Keywords:Quasi-Einstein Metric, Ricci Soliton, Steady, Expanding
拟爱因斯坦度量的分类
李金楠,高翔*
中国海洋大学数学科学学院,山东 青岛

收稿日期:2018年12月12日;录用日期:2018年12月27日;发布日期:2019年1月2日

摘 要
拟爱因斯坦度量(又称Ricci孤立子)是爱因斯坦度量的自然推广,在规范场论与超弦理论中有重要的应用,其研究有两个重要的方向:一是研究黎曼流形上拟爱因斯坦度量的结构对其几何及拓扑结构的影响;另一个是研究其几何性质与几何不变量。本文,我们将系统的阐述满足一定曲率条件、Weyl张量条件及Bach平坦等条件下梯度稳定及扩张拟爱因斯坦度量的分类。
关键词 :拟爱因斯坦度量,Ricci孤立子,稳定,扩张

Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
20世纪80年代,Hamilton [1] 提出了Ricci流的概念,实际上Ricci流最初引进是为了解决3维流形著名的Poincaré猜想(任意单连通的3维闭流形必同胚于3维闭球面)。拟爱因斯坦度量(又称Ricci孤立子)是Ricci流的自相似解 [2] 且经常出现在Ricci流方程的奇异点经伸缩变换后的极限中 [3] [4] [5] [6] 。一方面,拟爱因斯坦度量的研究有助于更好地理解Ricci流的奇异结构,从而结合几何手术的方法可以得到一些重要的几何和拓扑结果,是研究黎曼流形最有力的工具之一,因此它在几何分析和Ricci流的研究中具有重要的地位。另一方面,从微分方程的角度看拟爱因斯坦度量是爱因斯坦度量的自然推广 [7] ,在相对论、规范场论与超弦理论中有重要的应用,因此其分类对于数学及物理发展均具有重要的研究意义。
1.1. 拟爱因斯坦度量介绍
黎曼度量
,若其Ricci张量满足
(
为常数),则称为爱因斯坦度量。一个光滑流形
带有爱因斯坦度量,则称该流形为爱因斯坦流形,拟爱因斯坦度量是爱因斯坦度量的自然推广。光滑流形上的一个完备度量
称为拟爱因斯坦度量(又称Ricci孤立子),若存在光滑的向量场
使得其Ricci张量满足
为常数。此外,若V为一个梯度向量场,对光滑函数f满足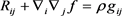 ,则称
为梯度拟爱因斯坦度量(梯度Ricci孤立子)。光滑函数f称为势函数。当
时称为稳定拟爱因斯坦度量,
称为收缩拟爱因斯坦度量,
时称为扩张的。本文我们将主要研究稳定及扩张拟爱因斯坦度量的分类。
,则称
为梯度拟爱因斯坦度量(梯度Ricci孤立子)。光滑函数f称为势函数。当
时称为稳定拟爱因斯坦度量,
称为收缩拟爱因斯坦度量,
时称为扩张的。本文我们将主要研究稳定及扩张拟爱因斯坦度量的分类。
由于 为度量 在方向V上的Lie导数,故上述Ricci方程分别可以写作 和 。注意到 (即f为常函数)的情况即g为爱因斯坦度量,因此拟爱因斯坦度量为爱因斯坦度量的自然推广,且经过适当的伸缩变换可标准化令 , , 。
1.2. 典型的拟爱因斯坦度量
众所周知,当 时存在非平凡的紧致梯度收缩拟爱因斯坦度量。同样的,也存在非爱因斯坦度量的完备非紧致的拟爱因斯坦度量,下面给出一些完备非紧致的典型的例子。
例1.1 (cigar孤立子) 2维流形上,Hamilton引进了第一个完备非紧致的拟爱因斯坦度量,称为cigar
孤立子,其度量为 ,势函数为 。特别地,cigar孤立子有正高斯曲率及线性的体积增长。
例1.2 (Bryant孤立子)黎曼流形 的情况下,高维完备非紧致的梯度稳定拟爱因斯坦度量由Bryant引进,Bryant孤立子为旋转对称的且具有正截面曲率且以r为半径的测地球 体积增长率为 。
例1.3 (Gaussian孤立子)具有平坦欧几里得度量的 也可以含收缩及扩张拟爱因斯坦度量,称为Gaussian收缩孤立子或扩张孤立子。
1) 为带有势函数 的梯度收缩Ricci孤立子, 。
2) 为势函数是 的梯度扩张Ricci孤立子, 。
梯度拟爱因斯坦度量为Hamilton-Ricci流的自相似解且对应于奇异模型,因而对于研究Ricci流至关重要。爱因斯坦广义相对论需要用弯曲空间来描述物理世界,黎曼流形为描述解释广义相对论提供了工具,因此研究黎曼流形上拟爱因斯坦度量的研究与分类有助于解决广义相对论及爱因斯坦场方程等问题。对其进行分类的关键是结合孤立子方程运用微分几何与几何分析的方法寻找与构造其上一些重要的几何不变量,建立一些有意义的几何估计、几何比较定理并计算一些拓扑不变量,最终结合黎曼几何与拓扑学的重要定理给出其分类结果。拟爱因斯坦度量的研究主要分为紧致与非紧致两大部分,在流形紧致的条件下,Perelman [2] 证明了拟爱因斯坦度量一定是梯度的,因此对紧致情况的研究可转化为对梯度拟爱因斯坦度量的研究。特别地,紧致稳定或扩张拟爱因斯坦度量必为爱因斯坦度量 [8] [9] ,且2、3维紧致收缩拟爱因斯坦度量也是爱因斯坦度量。Hamilton还证明了任意2维Ricci流的完备非平坦古典解若具有有界曲率,则必为 , 或cigar孤立子,2维拟爱因斯坦度量的分类已经十分完善且有很多非常好的结果。在流形完备非紧致的条件下,可以分为收缩、稳定、扩张的情形进行研究。关于收缩孤立子在另一篇文章中给出系统的阐述,本文,我们将主要研究稳定及扩张拟爱因斯坦度量的分类。
2. 梯度稳定拟爱因斯坦度量的分类
梯度稳定拟爱因斯坦度量为Ricci流的Type II奇异模型,紧致梯度稳定拟爱因斯坦度量必为Ricci平坦的,因此理解其分类及几何性质有助于更好的理解Ricci流解的渐近行为。2维稳定情形最著名的莫过于cigar孤立子,3维稳定拟爱因斯坦度量最著名的几个例子是 、 及Bryant孤立子。1998年Hamilton [1] 证明了2维流形上具有有界数量曲率(在流形某点上能达到最大值)或正Ricci曲率的稳定拟爱因斯坦度量必为cigar孤立子; 时,Bryant证明了在 上存在唯一的旋转对称的梯度拟爱因斯坦度量并构造了完备旋转对称、曲率算子为正的稳定拟爱因斯坦度量;同时,Cao-Chen [10] 证明了n维 ( ) 完备局部共形平坦的梯度稳定拟爱因斯坦度量等距于 或Bryant孤立子的一个有限商空间;特别地, 时,Chen-Wang [11] 证明了任意4维完备半共形平坦的梯度稳定拟爱因斯坦度量为Ricci平坦的或等距于Bryant孤立子;同梯度收缩孤立子, 时,Weyl张量及Bach张量的引进也产生很多相关的分类结果。利用Weyl张量的演化方程Catino-Mantegazza证明了Bryant孤立子是唯一的完备非紧致梯度稳定拟爱因斯坦度量。通过研究无穷远附近的渐近几何与Killing向量场,Brendle还证明了具有正截面曲率与渐近圆柱条件的梯度稳定拟爱因斯坦度量一定是旋转对称的。
定理2.1 (Brendle [12] )令 为一个3维稳定拟爱因斯坦度量,数量曲率为正且在无穷远处趋向于零,若存在有界区域 ,使得 ,则M为旋转对称的。其中函数 满足 。
2002年,Perelman [2] 提出著名的猜想:非平坦的k-非坍塌梯度稳定拟爱因斯坦度量必为Bryant孤立子。Brendle [13] 最终给出证明:
定理2.2 任意3维非平坦的k-非坍塌完备梯度稳定拟爱因斯坦度量 是旋转对称的,因而等距于Bryant孤立子。
在数量曲率满足一定的积分条件且截面曲率非负的情况下,Catino [14] 给出了梯度稳定拟爱因斯坦度量的一个分类:
定理2.3 令 为一个完备梯度稳定拟爱因斯坦度量, ,设其具有非负截面曲率且满足 ,则 等距于 或 的一个有限商空间,其中 为cigar孤立子。
在 时,减弱假设条件下可得一个类似的分类结果:3维完备梯度稳定拟爱因斯坦度量,若满足 ,则 等距于 或 的一个有限商空间。
结合拟爱因斯坦度量体积增长估计 [15] ,Catino-Mastrolia-Monticelli [14] 还证明了:
定理2.4 完备梯度稳定拟爱因斯坦度量 ( )若具有非负截面曲率及低于二次的体积增长形式,则为 的商空间。
特别地,3维情形下,曲率非负的条件显然成立 [16] ,这表明3维完备梯度稳定拟爱因斯坦度量 若具有低于二次的体积增长形式则为 的商空间。局部共形平坦的黎曼流形可以通过共形变化达到局部上与欧氏度量等价,因此局部共形平坦的条件对流形几何性质的研究起到较好的简化作用,特别可以使得黎曼曲率算子具有较简单的形式更便于研究,因此可以运用张量分析与活动标架的方法来计算Ricci孤立子方程在共形变化下的偏微分方程及其几何量在共形变换下的表达式,通过研究共形变换后的黎曼流形的几何结构反过来可以揭示原来的拟爱因斯坦度量分类结果。 时,自然会问:Bryant孤立子是否为唯一的局部共形平坦且具有正曲率的完备非紧致梯度稳定拟爱因斯坦度量?在Israel [17] 及Robnsono [18] 工作的基础上,Cao-Chen [10] 给出了肯定的答案:
定理2.5 一个n维局部共形平坦的且具有正截面曲率的完备非紧致梯度稳定拟爱因斯坦度量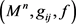 等距于Bryant孤立子。
等距于Bryant孤立子。
在此基础上,没有曲率假设条件时,他们还证明了n维局部共形平坦的的完备非紧致梯度稳定拟爱因斯坦度量为平坦的或等距于Bryant孤立子。
Bryant [19] 曾证明存在唯一非平坦的梯度稳定 拟爱因斯坦度量为 与R的乘积,在此基础上,Catino-Mantegazza [20] 给出以下命题:
推论2.6 任意n维局部共形平坦的梯度稳定Ricci孤立子为 或Bryant孤立子的商空间。
 时,Weyl张量定义为:
时,Weyl张量定义为:
同收缩拟爱因斯坦度量一样,高维情况下引进Weyl张量会得到许多非常好的分类定理。
定理2.7 (Cao-Chen [10] )设 ,任意n维Weyl张量为零( )的梯度稳定拟爱因斯坦度量为平坦的或等距于Bryant孤立子。
在此基础上且不需要假设额外的曲率条件,Chen-Wang [11] 证明了任意4维完备梯度稳定拟爱因斯坦度量若 ,则M必等距于Bryant孤立子或一个满足 且Ricci平坦的流形。
进一步减弱Weyl张量条件,Kim [21] 得到了一个具有调和Weyl张量的梯度稳定拟爱因斯坦度量的分类结果:
推论2.8 任意4维完备梯度稳定拟爱因斯坦度量 ,若 ,则M必为Ricci平坦的或等距于Bryant孤立子。
Bach张量定义为:
其中 为Weyl张量,Cotton张量 ,故Bach张量可表示为 。特别地, 时,有 。
时,根据Bach平坦也能得到很多关于稳定拟爱因斯坦度量的分类。特别地,Bach平坦表明局部共形平坦,能否在Weyl张量一阶消失的条件下获得类似的结果依然是一个有待解决的问题。
定理2.9
,令
为一个具有正曲率的完备稳定拟爱因斯坦度量,设其数量曲率R在流形内部某点能达到最大值且为Bach平坦的,则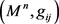 等距于Bryant孤立子。
等距于Bryant孤立子。
特别地, 时,他们还证明了3维完备梯度稳定拟爱因斯坦度量若满足 ,则M为爱因斯坦流形或为局部共形平坦的。显然Bach平坦或的条件比局部共形平坦更弱,因而结合3维局部共形平坦稳定拟爱因斯坦度量的结论,他们还证明了一个3维完备梯度稳定拟爱因斯坦度量若满足 则为Ricci平坦的或等距于Bryant孤立子。
3维张量 定义为:
其中 为 Schouten张量, 为爱因斯坦张量。给出 定义的基础上,Cao等人 [22] 还证明了如下定理:
定理2.10 令 为一个完备梯度稳定拟爱因斯坦度量满足 ,设其曲率为正且数量曲率R在流形内部某点能达到最大值,则 等距于Bryant孤立子。
特别地,Cao-Chen [23] 证明了任意4维完备梯度稳定拟爱因斯坦度量
若满足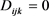 ,则M为Ricci平坦的或等距于Bryant孤立子。Catino-Mastrolia-Monticelli [24] 证明了任意满足
的3维完备梯度稳定拟爱因斯坦度量为
或Bryant孤立子的一个有限商空间,其中
时,
当且仅当
。
,则M为Ricci平坦的或等距于Bryant孤立子。Catino-Mastrolia-Monticelli [24] 证明了任意满足
的3维完备梯度稳定拟爱因斯坦度量为
或Bryant孤立子的一个有限商空间,其中
时,
当且仅当
。
3. 梯度扩张拟爱因斯坦度量的分类
梯度扩张拟爱因斯坦度量为Ricci流的Type III奇异模型且提供了Harnack不等式中满足等号的一些例子 [25] 。梯度扩张拟爱因斯坦度量很少能满足刚性,但是数学家们通过控制曲率条件、Weyl张量及Bach平坦条件等获得了许多分类结果。在2维情形,存在非平凡的完备非紧致的扩张拟爱因斯坦度量 [26] ;高维情形,Cao [27] 构造了完备非紧的扩张梯度Kähler-Ricci孤立子;Ricci曲率非负的完备非紧致拟爱因斯坦度量微分同胚于欧氏空间;Chen-Zhu [28] 还证明了曲率算子非负且Ricci曲率严格正的Type III奇异模型,当tR达到最大时必为同痕的扩张拟爱因斯坦度量。特别地,完备非紧致的梯度扩张拟爱因斯坦度量的数量曲率有下界。
定理3.1 (Peterman-Wylie [29] )具有常曲率的3维梯度扩张拟爱因斯坦度量必为 , 或 的商空间。
前面我们已经提到紧致的扩张拟爱因斯坦度量必为爱因斯坦流形,通过添加 空间有关量及适当的势函数积分条件,Pigola-Rimoldi-Setti [30] 证明了以下结论:
定理3.2 对 ,若 ,则任意完备的梯度扩张拟爱因斯坦度量 为爱因斯坦流形(平凡孤立子)。
结合数量曲率条件,他们还证明了完备梯度扩张拟爱因斯坦度量,若其数量曲率满足 且 ,则M等距于标准的欧氏空间;特别地, 时,3维完备梯度扩张拟爱因斯坦度量若具有非负Ricci曲率且 ,则M等距于 。进一步, [22] 中还证明了 时,任意具有非负Ricci曲率的完备Bach平坦的梯度扩张拟爱因斯坦度量必为旋转对称的; 时,任意具有非负Ricci曲率且满足 的完备梯度扩张拟爱因斯坦度量必为旋转对称的。
Brendle [13] [31] 证明了具有正截面曲率的梯度稳定拟爱因斯坦度量附加额外条件时必为旋转对称的。在此基础上,扩张情况下Chodosh [29] 证明了:
定理3.3 具有正截面曲率且渐近圆锥的梯度扩张拟爱因斯坦度量为旋转对称的。
与梯度稳定Ricci孤立子相似,Kim [21] 还证明了扩张情形的分类结果:
定理3.4 一个4维完备梯度扩张拟爱因斯坦度量 若具有调和Weyl张量,即 ,则符合以下情况之一:
1) 势函数f为常数函数, 为爱因斯坦度量;
2) 等距于的 一个有限商空间,其中 为2维黎曼流形且具有常曲率 、且其势函数为 ;
3) 为局部共形平坦的。
Ricci流的齐次解相对简单且出现在Ricci流的极限中,长期以来也得到诸多研究及重要进展。此外,在没有爱因斯度量时,齐次Ricci孤立子度量自然是一个非常不错的选择,因此齐次Ricci孤立子空间的分类也一直是微分几何的一个核心问题,其中Jablonski [32] 给出了有关齐次拟爱因斯坦度量的分类定理:任意紧致齐次的拟爱因斯坦度量必为爱因斯坦度量。希望得到的黎曼流形上拟爱因斯坦度量的研究与更为精确的分类能够更好地应用于解决广义相对论及爱因斯坦场方程等问题。
基金项目
本文由山东省自然科学基金(ZR2018MA006)及山东省研究生导师指导能力提升项目(SDYY17009)支持。
文章引用
李金楠,高 翔. 拟爱因斯坦度量的分类
Classification of Quasi-EinsteinMetric[J]. 现代物理, 2019, 09(01): 12-18. https://doi.org/10.12677/MP.2019.91002
参考文献
- 1. Hamilton, R.S. (1998) The Ricci Flow on Surfaces. Contemporary Mathematics, 71, 237-261.
https://doi.org/10.1090/conm/071/954419 - 2. Perelman, G. (2002) The Entropy Formula for the Ricci Flow and Its Geometric Applications. arXiv: math. DG/0211159.
- 3. Perelman, G. (2003) Ricci Flow with Surgery on Three-Manifolds. arXiv: math.DG/0303109.
- 4. Perelman, G. (2003) Finite Extinction Time for the Solutions to the Ricci Flow on Certain Three-Manifolds. arXiv: math. DG/0307245.
- 5. Hamilton, R.S. (1982) Three Manifolds with Positive Ricci Curvature. Journal of Differential Ge-ometry, 17, 255-306.
https://doi.org/10.4310/jdg/1214436922 - 6. Hamilton, R.S. (1993) Eternal Solutions to the Ricci Flow. Journal of Differential Geometry, 38, 1-11.
https://doi.org/10.4310/jdg/1214454093 - 7. Cao, H.D., Chen, B.L. and Zhu, X.P. (2008) Recent Developments on Hamilton’s Ricci Flow. Surveys in Differential Geometry, 47-112.
- 8. Hamilton, R.S. (1993) The Formation of Singularities in the Ricci Flow. Surveys in Differential Geometry, 2, 7-136.
https://doi.org/10.4310/SDG.1993.v2.n1.a2 - 9. Ivey, T. (1993) Ricci Solitons on Compact Three-Manifolds. Differential Geometry and Its Applications, 3, 301-330.
https://doi.org/10.1016/0926-2245(93)90008-O - 10. Cao, H.D. and Chen, B.L. (2012) On Locally Conformally Flat Gradient Steady Ricci Solitons. Transactions of the American Mathematical Society, 634, 2377-2391.
https://doi.org/10.1090/S0002-9947-2011-05446-2 - 11. Chen, X.X. and Wang, Y.Q. (2015) On Four-Dimensional An-ti-Self-Dual Gradient Ricci Solitons. The Journal of Geometric Analysis, 25, 1335-1343.
https://doi.org/10.1007/s12220-014-9471-8 - 12. Brendle, S. (2010) Uniqueness of Gradient Ricci Solitons. arXiv: math. DG/1010.3684v2.
- 13. Brendle, S. (2013) Rotational Symmetry of Self-Similar Solutions to the Ricci Flow. Inventiones Mathematicae, 194, 731-764.
https://doi.org/10.1007/s00222-013-0457-0 - 14. Catino, G., Mastrolia, P. and Monticelli, D.D. (2016) Classification of Expanding and Steady Ricci Solitons with Integral Curvature Decay. Geometry & Topology, 20, 2665-2685.
https://doi.org/10.2140/gt.2016.20.2665 - 15. Deruelle, A. (2012) Steady Gradient Ricci Soliton with Curvature in L1. Commu-nications in Analysis and Geometry, 20, 31-53.
https://doi.org/10.4310/CAG.2012.v20.n1.a2 - 16. Chen, B.L. (2009) Strong Uniqueness of the Ricci Flow. Journal of Differential Geometry, 82, 363-382.
https://doi.org/10.4310/jdg/1246888488 - 17. Israel, W. (1967) Event Horizons in Static Vacuum Space-Times. Physical Review, 164, 1776-1779.
https://doi.org/10.1103/PhysRev.164.1776 - 18. Robnsono, D.C. (1997) A Simple Proof of the Generalization of Isarel’s Theo-rem. General Relativity and Gravitation, 8, 695-698.
- 19. Bryant, R.L. (1987) Locally Existence of Gradient Ricci Soli-tons.
- 20. Catino, G. and Mantegazza, C. (2013) The Evolution of the Weyl Tensor under the Ricci Flow. Annales-Institut Fourier, 61, 1407-1435.
https://doi.org/10.5802/aif.2644 - 21. Kim, J. (2016) On a Classification of 4-D Gradient Ricci Solitons with Harmonic Weyl Curvature.
- 22. Cao, H.D., Catino, G., Chen, Q., Mantegazza, C. and Mazzieri, L. (2014) Bach-Flat Gradient Steady Ricci Solitons. Calculus of Variations & Partial Differential, 49, 125-138.
https://doi.org/10.1007/s00526-012-0575-3 - 23. Cao, H.D. and Chen, Q. (2009) On Complete Gradient Shrinking Ricci Solitons. Journal of Differential Geometry, 85, 175-185.
https://doi.org/10.4310/jdg/1287580963 - 24. Catino, G., Mastrolia, P. and Monticelli, D.D. (2017) Gradient Ricci Solitons with Vanishing Conditions on Weyl. Journal De Mathématiques Pures et Appliquées, 108, 1-13.
https://doi.org/10.1016/j.matpur.2016.10.007 - 25. Hamilton, R.S. (1993) The Harnack Estimate for the Ricci Flow. Journal of Differential Geometry, 37, 225-243.
https://doi.org/10.4310/jdg/1214453430 - 26. Chow, B., Lu, P. and Ni, L. (2006) Hamilton’s Ricci Flow. Grad. Stud. Math, Vol. 77, AMS.
- 27. Cao, H.D. (1997) Limitations of Solutions to the Kähler-Ricci Flow. Journal of Differential Geometry, 45, 257-272.
https://doi.org/10.4310/jdg/1214459797 - 28. Chen, B.L. and Zhu, X.P. (2000) Complete Riemannian Manifolds with Pointwise Pinched Curvature. Inventiones Mathematicae, 140, 423-452.
https://doi.org/10.1007/s002220000061 - 29. Petersen, P. and Wylie, W. (2010) On the Classification of Gradient Ricci Solitons. Geometry & Topology, 14, 2277-2300.
https://doi.org/10.2140/gt.2010.14.2277 - 30. Pigola, S., Rimoldi, M. and Setti, A.G. (2011) Remarks on Non-Compact Gradient Ricci Solitons. Mathematische Zeitschrift, 268, 777-790.
https://doi.org/10.1007/s00209-010-0695-4 - 31. Brendle, S. (2013) Rotational Symmetry of Ricci Solitons in Higher Dimensions. Journal of Differential Geometry, 97, 191-214.
https://doi.org/10.4310/jdg/1405447804 - 32. Jablonski, M. (2015) Homogeneous Ricci Solitons. Journal für die Reine und Angewandte Mathematik, 699, 159-182.
https://doi.org/10.1515/crelle-2013-0044
NOTES
*通讯作者。