Modern Physics
Vol.
09
No.
05
(
2019
), Article ID:
31939
,
21
pages
10.12677/MP.2019.95023
Wave Functions in Quantum Mechanics and the New Concept of Matter Waves
—And Fundamental Reconstruction of Quantum Mechanics
Daqing Li
China Wood Luoding Cement Co. Ltd., Luoding Guangdong

Received: Aug. 4th, 2019; accepted: Aug. 22nd, 2019; published: Aug. 29th, 2019

ABSTRACT
Because the experiment proves that the Copenhagen about “wave function does not represent the real matter waves but subjective in the sense of probability wave” point of view is wrong, the wave function is objective in description of matter waves, thus to reveal the form of the objective existence of matter waves and properties, this article embarks from the concept of DE Broglie wave guide, by analogy with Einstein’s theory of light quantum theory, puts forward that any column objective existence of matter wave energy is quantized, the particle is accompanied with the assumption, the quantized energy existing in the matter waves on the basis of analysis found that any column in the form of matter waves are waves, thus the new concept of wave of matter must and can only be described by wave functions in quantum mechanics. After analyzing and reasoning, the following conclusions are obtained: the matter wave of any particle follows the superposition principle of matter wave; Schrodinger equation in quantum mechanics can be established from the concept of matter wave. The statistical interpretation of wave function can be understood by means of the concept of matter wave, and Schrodinger’s cat paradox and EPR paradox (or quantum entanglement) can also be solved on the basis of the new concept of matter wave. The uncertainty relation in quantum mechanics can be explained by the concept of matter wave. The concept of matter wave is falsifiable, and its existence has been verified by physical experiments, so it is a scientific concept.
Keywords:Material Wave, Energy, Quantization, Particle, Wave Field, Virtual Wave, Wave Function
量子力学中的波函数与新概念物质波
——暨量子力学的基础重建问题
李大庆
中材罗定水泥有限公司,广东 罗定

收稿日期:2019年8月4日;录用日期:2019年8月22日;发布日期:2019年8月29日

摘 要
由于实验证明哥本哈根关于“波函数不代表真实的物质波而是主观意义上的概率波”的观点是错误的,波函数描述的物质波具有客观性,因而为揭示客观存在的物质波的存在形式及属性,本文从德布罗意引导波概念出发,通过与爱因斯坦的光量子理论的类比,提出任何一列客观存在的物质波的能量都是量子化的、与之相伴随的粒子是其量子化的能量的假设,并在此基础上通过对物质波存在形式的分析发现任何一列物质波都是虚波,从而新概念物质波必须且只能用量子力学中的波函数进行描述。后经分析推理获得以下结论:任何粒子的物质波都遵循物质波的叠加原理;量子力学中的薛定谔方程等均可从物质波概念出发得以建立;波函数的统计解释可借助物质波概念得以理解,薛定谔猫悖论及EPR悖论(或量子纠缠)也可以在新的物质波概念基础上得以解决;量子力学中的测不准关系可以借助物质波概念进行诠释;物质波概念具有可证伪性,其存在已获有关物理学实验的证实,因而是科学的概念。
关键词 :物质波,能量,量子化,粒子,波场,虚波,波函数

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
非相对论量子力学的第一个完整理论体系是德国物理学家W·海森堡(W. Heisenberg)于1925年所创建的以力学量为核心、以矩阵为基本数学结构、以力学量之间的对易关系为运算单元的矩阵力学。1926年,奥地利物理学家E·薛定谔(E. Schrödinger)在法国物理学家L·德布罗意(L. de Broglie)于1923年提出的引导波概念基础上建立了薛定谔方程及波动力学体系,并证明了矩阵力学与波动力学之间的等价关系。之后物理学界虽然对薛定谔波动方程中描述物质波的波函数的物理意义有过激烈争论,但最终还是德国物理学家马克斯·玻恩(Max Born)对波函数的统计解释被学界所广泛接受。此后,奥地利物理学家W·泡利(W. Pauli)于1925年提出不相容原理、英国物理学家P·狄拉克(P. Dirac)于1928年建立以接近光速运动的电子的相对论方程、德国物理学家冯·诺依曼(Von Neumann)于1935年证明量子力学理论体系的自洽性、美国物理学家R·费曼(R. Feynman)于1942年建立量子力学的路径积分理论等事件则标志量子力学理论体系的日趋成熟。二十世纪下半叶,物理学家借助量子力学理论体系已经能解决几乎所有微观粒子的相关问题,非相对论量子力学因此被公认为人类历史上最成功的理论。虽然如此,但几乎自量子力学理论体系创立之初起,学界对粒子的所谓波粒二象性的本质、波函数的本质、微观粒子的运动是决定论还是非决定论以及量子力学是否是完备的理论等一系列问题就一直处于争论中,其中以爱因斯坦与波尔之间的争论持续时间最长,对量子力学的影响最为深远,而且这种争论至今仍在持续、远没有最终定论。在与爱因斯坦的争论过程中,最终以波尔为代表的哥本哈根学派的观点为物理学界普遍接受,其主要观点为:在量子力学中,粒子的空间坐标由满足薛定谔方程的波函数描述,该波函数不代表客观存在的物质波而是主观意义上的概率波,其模的平方表示粒子以某一物理量在某一空间坐标上出现的概率,因而微观粒子的物理量在本质上具有不确定性、既不满足决定论也不遵循因果律 [1] [2] 。这种对微观粒子的所谓波粒二象性的诠释完全建立在人的主观意识基础之上,从而导致量子力学中两个著名的悖论:即薛定谔猫悖论与EPR悖论,这两个悖论至今未找到解决方法。
由于概率只是现象出现的可能性而非导致现象发生的机制,因而哥本哈根学派的观点并不能令所有物理学家满意,针对其“波函数不代表真实的物质波而只是主观意义上的概率波”的观点,历史上曾有物理学家提出与之完全不同的理论,如德布罗意提出的双重解理论及玻姆提出的量子势理论等,这些理论的出发点是波函数背后有一个客观存在的对象,而该对象才是导致粒子的波粒二象性的根本原因,但这些理论都因固有的问题没有被物理学家普遍接受。而清华大学龙桂鲁教授于2018年所做的一项实验则有力地支持了波函数描述的对象具有客观实在性的观点,从而根本上否定了哥本哈根学派关于“波函数不代表真实的物质波而是主观意义上的概率波”的观点,换句话说不存在所谓的概率波,只存在对微观现象的(玻恩)概率解释。据此实验,龙教授提出了波函数的实在论诠释,认为波函数是微观物体的存在方式,确切地说,微观物体以波函数的形式弥散在空间中,同时具有振幅和相位,以小于或等于光速的速度传播 [2] ,但由于这种观点无法与微观粒子在任何时候都表现出的颗粒性特征相协调,因而无法被广泛接受。那么波函数描述的客观存在的对象其存在形式如何、遵循哪些基本规律、其基本方程是什么?本文将在德布罗意物质波概念(确切说是引导波概念,而德布罗意的物质波概念乃至包括薛定谔建立其波动方程时所使用并沿用至今的物质波概念其内容都非常模糊,而且从未有人明确其具体的存在形式)基础上,通过与爱因斯坦光量子理论的类比,提出任何一列客观存在的物质波的能量都是量子化的、与之相伴随的粒子就是其量子化的能量的假设,并在此基础上通过对物质波存在形式的详细分析发现任何一列物质波都必须且只能是虚波,从而物质波的波振幅无法用实数而必须要用复数描述,确切地说物质波必须且只能用量子力学中的波函数进行描述,而这正是本文提出的新概念物质波完全不同于量子力学中现有的物质波概念之处。而后在新概念物质波基础上经分析推理获以下结论:任何粒子的物质波都必须遵循物质波的叠加原理,而这正是所谓粒子的态的叠加原理的本质,并且各种微观粒子的双缝干涉及单缝衍射现象都是物质波的叠加原理的具体体现;从描述物质波的波函数出发可以建立物质波的波动方程(量子力学中的薛定谔方程、克莱因–高登方程及狄拉克方程等则是在不同速度条件下物质波的波动方程的具体形式),并进而重建量子力学理论体系;波函数统计解释的本质为用于描述粒子的态的波函数其描述的对象就是客观存在且其能量具有量子化特征的物质波,薛定谔猫悖论及EPR悖论(或量子纠缠)也可以在新的物质波概念基础上得以圆满解决;粒子的任意两个具有非对易关系的力学量之间都存在的测不准关系是波函数所描述的物质波的叠加原理的具体表现形式;物质波概念具有可证伪性,其存在已获得有关物理学实验的证实,因而是科学的概念。特别是由于本文将量子力学建立在客观存在的、用波函数描述的物质波而非主观(及虚幻)意义的概率波基础之上,因而量子力学中所有有关内容都可以得到合理诠释(而这是量子力学中现有的物质波概念所无法实现的),从而证明了波函数描述的是客观存在的物质波而非主观意义上的概率波,下面将进行详细论述。
2. 物质波及其能量与动量
由爱因斯坦的光量子理论可知,任何一列光(波)所具有的能量都是量子化的,其量子化的能量E由微观尺度的单个光子所携带(该光子即是其光(波)的量子化的能量E也被称作光量子),并且如果一列单色平面光(波)的角频率ω (=2πγ,γ为光波的频率)、波数k (=2π/λ,λ为光波的波长),则其光子的能量为恒定值 、动量为恒定值 , 为普朗克常数。而德布罗意的物质波(简称d-物质波)理论则假设,任何一个微观粒子都有一列客观存在的而非虚构想象的d-物质波与之相伴随 [3] ,如果某一自由运动的粒子的能量为恒定值E、动量为恒定值p,则与之伴随的d-物质波是角频率为ω、波数为k的单色平面波,并且该粒子的能量为 、动量为 ,其中 为普朗克常数,此即德布罗意关系式;由于包括光子在内的任何类型的自由运动的粒子的能量E及动量p和与之伴随的单色平面d-物质波的角频率ω及波数k之间均存在同一组数量关系 、 ,并且这一结论已经得到迄今为止所有相关科学实验的验证,特别是由于角频率及波数分别为ω及k的一列波与角频率及波数分别为 及 的另一列相同类型的波在同一直线上以相同方向传播并相遇叠加后的波群的群速度 为其相对于观者的能量传播的速度,并且由此可以证明单色平面d-物质波相对于观者的能量传播的速度Vg等于与之伴随的自由粒子相对于观者的运动速度V,即
(1)
因此,粒子和与之伴随的d-物质波之间不可能仅仅只是简单的伴随关系。类比爱因斯坦的光量子理论,同时考虑到所有关于微观粒子的物理实验中只能观测到一个个完整的、不可分割的、具有确定物理属性的、在任一时刻都只能出现在一个局域空间位置上的粒子这一事实,以及清华大学教授龙桂鲁先生于2018年所做的证明波函数描述的对象具有客观实在性的实验,在此可以合理地假定:任何一列包括光波在内的新概念物质波(不同于d-物质波,以下简称物质波)都是客观存在的、所具有的能量E都是量子化的,该量子化的能量均由与之相伴的微观尺度的一个粒子所携带(该粒子即是其物质波的量子化的能量,其携带的能量显然属于整列物质波,因而也可称该粒子为其物质波的能量子),并且如果物质波的角频率为ω、波数为k,相伴粒子的能量为E、动量为p,则有关系 、 ,其中ћ为普朗克常数。
由于任何一列波都具有能量,波因具有能量而稳定存在且波所携带的能量随波的传播而得以在空间中不断向远处传输,因而波与其携带的能量两者间并非简单的偶合关系,而是互为前提、相互依存的不可分割的整体;既然粒子是其物质波的量子化的能量,那么物质波必然因其具有量子化的能量–粒子–而稳定存在,粒子也将随其物质波的传播而不断运动,因而物质波与其粒子之间互为前提、相互依存,共同构成相生相伴、永不可分的整体;确切地说,物质波与其粒子两者都不可能脱离对方而独立存在,并且借助任何方法也不可能将两者割裂开来,因而当我们谈论物质波时都是指粒子的物质波,而谈论粒子时则是指物质波的粒子。由狭义相对论可知,相对于观者以速度V运动的粒子的(同时也是其物质波的)运动质量为m、能量E及动能Ek分别为
(2)
(3)
其中C为光速, ,m0为粒子的静止质量。粒子的(同时也是其物质波的)动量则为
(4)
从而粒子的(同时也是其物质波的)能量E与动量p之间有关系为
(5)
3. 物质波的存在形式及其描述方法
由于物质波的能量是量子化的并且物质波的量子化的能量由其粒子所携带,因此,物质波的存在形式必定不同于物理学中所论及的其能量具有连续性分布特征的各种形式(如普通机械波及经典电磁波等)的波;另外,由于建立在德布罗意关于粒子的能量及动量与其物质波的角频率及波数之间重要的关系( 、 )基础之上的量子力学(薛定谔方程)理论体系已被到目前为止的所有相关物理实验证明为是正确的,因此,物质波概念也必定会因其与量子力学理论体系之间深刻的联系而被证明为是正确的,以下将对此进行深入讨论。
3.1. 物质波的存在形式
波的存在形式是指波从产生到由近及远地传播的全过程。我们知道,任何形式的波都可以看作是在特定的场中连续不断地传播着的:如声波是在分布于足够大空间区域内的气体分子或液体分子或固体原子等构成的场中传播的波;水面波是在处于重力环境下的液态水的表面水分子构成的场中传播的波;电磁波则是在电磁场中传播的波……等等。为便于问题的讨论,我们将波在其中得以传播的场称作波场,并且任何波场都由在某一层次上无法进一步分割的微小单元构成,我们将构成波场的这种微小单元称作微元(在机械波概念中则称其为质点)。显然,所有波在连续不断地传播过程中其波场的任何微元随波的传播都不会远离其平衡位置而只会在其平衡位置附近按一定规律做周期性振动(或振荡),而正是由于波场的相邻微元之间协同的、不间断的周期性振动才能使其以波的形式传播出去,从而波场的微元的周期性振动是波得以传播及波的能量借助其波载体从空间中一个位置传输至另一个位置并起作用的前提条件。另外,由于任何物质单元只有且必须在具有能量从而在能量作用条件下才能发生空间位移,并且这种空间位移都能通过物质单元与光之间的能量交换而被直接观测到从而具有可观测性同时必须且只能用实数描述(故也可称作实位移),因而任何形式的波其波场的微元发生可观测的周期性振动(也可称作周期性实振动)的前提条件是这些微元必须要具有能量。由于各种机械波及经典电磁波等所携带的能量是按波的能量分布规律连续分布于其波场的每一个微元上的(即这些波的波场的所有微元都具有能量),因而这些微元的周期性振动具有可观测性(即为周期性实振动),在此也可称这些波为实物波。
由于物质波是一种客观存在的波,因而必然会(如同普通机械波及经典电磁波那样)随其波场的微元的周期性振动由近及远连续不断地传播。同时由于任何一列物质波在传播过程中其能量并非如普通机械波及经典电磁波那样按波的能量分布规律连续分布于其波场的每一个周期性振动着的微元上的,而是量子化的、全部集中在微观尺度范围内的一个粒子上并由该粒子所携带,另由波场的微元的定义可知,粒子并非其物质波的波场的微元,因而物质波的波场的所有周期性振动着的微元都不具有能量从而其振动无法被任何仪器直接观测到,也就是说物质波的波场的微元的周期性振动不具有可观测性从而不可能是周期性实振动而只能是与之结构形式完全不同的周期性虚(显然不同于“无”)振动,并且其振幅也无法用实数表示而是必须要用非实数进行描述,而这就是迄今为止人们无法且永远无法直接观测到物质波的根本原因,因而物质波必须是且只能是一种客观存在的而非虚构想象的、其结构形式与实物波完全不同的波——虚波,虽然如此,我们仍按习惯称其为物质波。由于物质波的波振幅就是其波场的微元的周期性振动的幅度,因而物质波的波振幅也不可能是实数而只能是非实数,而数学中的非实数有复数(二元数)及超复数(如四元数、八元数等),在此我们可以很自然地采用最简单的非实数——复数(学界也有用更复杂的非实数如四元数及八元数等超复数来描述微观现象的各种尝试),也即物质波的波振幅只能是复数。这一全新的物质波概念显然不同于量子力学中现有的(其内容模糊、存在形式不详的) d-物质波概念,但与量子力学中微观粒子的态的波函数的描述方式则完全一致,并且同时也是量子力学中的波函数必须且只能采用复函数的根本原因,因而可以作为人们从根本上理解微观现象的本质的依据。
3.2. 物质波的描述方法
由于任何形式的波因其波场的所有微元都在其平衡位置附近协同的周期性振动而在波场中连续不断的传播着,因而无论在时间上还是空间上都必将表现出严格的周期性,这就意味着任何波都由振幅A、角频率ω及波数k等要素构成。而由于新概念物质波是虚波、其振幅是复振幅,因而必须要用含有复振幅Ψ、角频率ω及波数k的复函数来描述。显然,量子力学中用于描述微观粒子状态的波函数 就是完全符合新概念物质波描述条件的函数,因而新概念物质波可直接用波函数 来进行描述,换言之,量子力学中被认为用于描述微观粒子的态的波函数其真正描述的对象就是客观存在的、其能量具有量子化特征的新概念物质波而非主观意义上的概率波,从而波函数被赋予了客观的内容;而正因为波函数正确模写了(以虚波形式存在的)新概念物质波,所以波函数能正确描述微观粒子的运动规律并由此印证新的物质波概念的正确性。因而单色平面物质波可用如下形式的波函数 进行描述
(6)
其中ω为物质波的角频率, 为物质波的波失,n为单位矢量(其方向与物质波的传播方向相同),Ψ0为物质波的复振幅。而由于物质波的(自由运动的)粒子的能量 ,动量 , 为普朗克常数(由于其值非常小,因而自由粒子的物质波的角频率ω及波数k的值均很大)。则上式又可表达为
(7)
此即自由运动的粒子的单色平面物质波。该表达式真正体现了物质波与其粒子之间不可分割的整体性关系,同时也体现了物质波的虚波特征。
由于物质波是一种波,因而必须遵循波的叠加原理(下面将进行讨论),这就意味着任意形状的物质波都可以看作是多个不同波长(分别对应于其粒子的不同动量)的单色平面物质波的叠加的结果,确切地说任意形状的物质波的波函数 都可以看作是不同动量的单色平面物质波的傅里叶变换所得。以下就是一般形状的物质波波函数 的傅里叶变换表达式
(8)
式中
(9)
其中
是以物质波的粒子的动量p为自变量的波函数,表达式(8)及(9)同样体现了物质波与其粒子之间不可分割的整体关系;显然,以上两式中的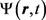 及
及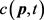 互为傅里叶变换式,由于各种量子力学文献中对此都有较详细的论述,在此就不加赘述。
互为傅里叶变换式,由于各种量子力学文献中对此都有较详细的论述,在此就不加赘述。
4. 物质波须遵循的规律
波动现象是自然界中普遍存在的一类现象,也是能量实现远距传输的一种重要方式。自然界中虽然存在形式多样的波,但却都以类似的方式存在并传播着(即都是波场的微元的周期性振动在空间及时间上的延续),因此,各种波都必须遵循一些相同的规律,特别是波的叠加原理——这种只有波动现象才具有的规律,从而我们也可以将波定义为遵循波的叠加原理的一类现象。正是由于波遵循波的叠加原理,因此才能产生其特有的现象如波的双缝干涉及单缝衍射。由于物质波也是一种波,因此也必须遵循只有波才具有的规律,即物质波的叠加原理,而所谓的粒子的双缝干涉及单缝衍射现象就是物质波的叠加原理起作用的具体表现形式,而这些现象如果不采用物质波概念进行解释就很难理解,以下将对此进行详细讨论。
4.1. 物质波的叠加原理
波的叠加原理是关于波的重要原理,是定量理解及计算波的双缝干涉及单缝衍射现象的理论依据,普通的机械波与经典电磁波都遵循波的叠加原理。所谓波的叠加原理可表述为:当同一波场中同时存在n列(可以用线性波动方程描述的)同一类型的波时,每一列波都将保持各自的传播规律不变且互不干扰;在这n列波相遇的区域里,该波场的任何一个微元振动的物理量等于每一列波在该微元上引起的振动的物理量的(矢量)和;在这n列波相遇的区域里,该波场的任何一个微元都同时参与n个振动,其振动的位移等于这n列波分别在该微元上引起的位移的矢量和,而当这n列波的振动方向在同一直线上时,这n个位移的矢量和在选定正方向后可简化为代数和。波的叠加原理也可以等效的表述为波的叠加原理:如果同一波场中存在n列同一类型的波 ,则
(10)
也是可能的一列波(其中 是任意实数)。
由于物质波是一种波,因此必须如普通机械波或经典电磁波那样起作用并遵循波的主要规律,特别是波的叠加原理,而量子力学的各种文献中所介绍的关于电子、质子、中子乃至分子等的双缝干涉及单缝衍射试验本质上就是这些粒子的物质波的双缝干涉及单缝衍射现象,确切地说是物质波的叠加原理的具体体现。显然,物质波的叠加原理与上述波的叠加原理的内容基本相同,只不过由于物质波的能量是量子化的,因而物质波的叠加原理必须反映其能量的量子化特点,同时还必须兼顾各种量子力学的有关实验。综上所述,关于物质波的叠加原理(在量子力学中则被称作粒子的态叠加原理)可表述如下:
物质波的叠加原理:如果在一个粒子的物质波波场中存在n列该粒子的物质波 ,则这n列物质波的线性叠加
(11)
同样也是该粒子可能的一列物质波(其中 为该粒子的物质波的波函数; 是任意复数)。
由式(11)可见,物质波的叠加原理与量子力学中粒子的态叠加原理具有完全相同的数学形式,但两者的物理意义却完全不同。物质波的叠加原理反映的是物质波的波动属性,因此可以作为波的叠加原理的一个特例顺理成章的提出来,其意义非常直观;而量子力学中的态叠加原理则完全是为了拟合所谓粒子的波动性的实验结果所做的人为假设,其意义抽象难懂,甚至到目前为止物理学家对其还没有清晰统一的认识,而由以上讨论可知,其本质就是物质波的叠加原理,因此,物质波的叠加原理是直观地理解量子力学中所谓粒子的波动性的理论依据。
4.2. 物质波的干涉及衍射
正是由于物质波遵循波的叠加原理,同时物质波的波长非常小,因此,当物质波遇到开有宽度及间距足够窄(尺度接近物质波的波长)的两条狭缝的平板并通过平板上的这两条狭缝时会产生双缝干涉现象;而当物质波遇到开有宽度足够窄(尺度接近物质波的波长)的一条狭缝的平板并通过平板上的这条狭缝时则会产生单缝衍射现象。这就是量子力学中所谓粒子的双缝干涉及单缝衍射现象的本质,也是物质波作为波所必然具有的性质,下面对此进行讨论。
物质波的双缝干涉即量力力学中所谓的粒子的双缝干涉,是同一类型的众多具有相同运动速度及质量的粒子通过双狭缝后在成像屏上产生明暗相间的条纹的现象。由于物理学家并不认为量子力学中的波函数描述了任何客观存在的对象,而是将波函数看作其模的平方与在空间中任意一点上找到相应粒子的概率成正比的概率波并且无法如真实的波那样发生双缝干涉现象,从而只能将粒子的双缝干涉现象解释为是粒子以某种人类无法想象的方式同时通过两条狭缝后发生的自干涉现象,这显然是一种没有且永远无法用任何物理实验进行验证的猜测,因为任何用于确定电子是否同时通过双狭缝的观测行为都将导致双缝干涉现象的彻底消失 [4] ,可见这种解释怪异诡辩、充满争议但又实属无奈。以下我们将采用物质波概念进行解释,图1为电子的双狭缝干涉实验示意图,实验装置由电子枪E、刻有单狭缝T的平板A、刻有双狭缝S1及S2的平板B及成像屏C构成,S1S2 = l,U为S1S2的中点,平板B与成像屏C之间的间距为UN = L。放置于图中左侧的电子枪向平板A垂直发射自由电子(电子的速度为V,能量为E,动量为p,其物质波的频率为γ、角频率为ω,波长为λ、波数为k),其中部分电子及其物质波穿过平板A单狭缝T后射向平板B,当电子的单色物质波ψ遇到并穿过B上的两条狭缝后分裂成两列子波ψ1及ψ2,并最终投射到屏C上。根据物质波的叠加原理,当波ψ1及ψ2在屏C上的一点M相遇时,如果两者到该点的行程之差S2V为物质波波长λ的整数倍nλ时,则在该点上两列物质波为“波峰与波峰”或“波谷与波谷”的叠加,屏C上显示为亮条纹;而如果两者到该点的行程之差S2V为物质波波长λ的整数倍 的1/2 (即 )时,则在该点上两列物质波为“波峰与波谷”或“波谷与波峰”叠加从而相互抵消,屏C上显示为暗条纹。需要特别说明的是,此处(及以下)借用实物波的“波峰”及“波谷”概念只是为了更形象化地理解物质波的叠加原理,并非其真实含义。由于物质波是虚波,其“波峰”及“波谷”也是虚的从而不具有可观测性,并且只有在具体的效应中才能反映出其与实物波的“波峰”及“波谷”之间的对应关系,因而实际情况要比实物波复杂得多,下面将进行具体分析。图中S1M = VM, , ,若假定穿过双狭缝的S1缝的子波ψ1到达屏C上的M点的复振幅为 ,则穿过双狭缝中的S2缝的子波ψ2到达屏C上的M点的复振幅显然为 ,据物质波的叠加原理,物质波在M点的复振幅Ψ0为ψ1及ψ2的复振幅之和
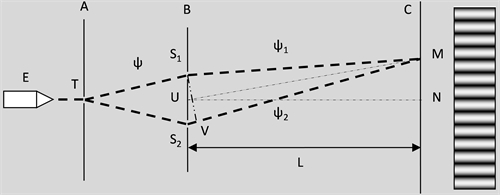
Figure 1. Experimental diagram of electronic double-slit interference
图1. 电子的双缝干涉实验示意图
(12)
由于Ψ0为复函数,因而Ψ0在M点的强度等于Ψ0的模的平方 (见以下讨论,物质波在空间中某一点上的强度与其振幅的模的平方成正比),同时利用 及三角函数的二倍角等公式则有
(13)
当 等于 时, 为最大值,因而有
(14)
即当
时,Ψ0在M点的强度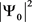 为最大值(即在屏C上显示为亮点);而当
等于
时,
为最小值,因而有
为最大值(即在屏C上显示为亮点);而当
等于
时,
为最小值,因而有
(15)
即当 时,Ψ0在M点的强度 为最小值(即在屏C上显示为暗点)。由以上计算过程可见,电子的物质波的双缝干涉现象的直接原因就是物质波的叠加原理。物理学家分别于1961年及1989年完成了较强电子源及极弱电子源的电子的物质波的双缝干涉实验,这两个实验都以极高的精度证明了以上分析的正确性。实际上,还可以用其他各种粒子的物质波的双缝干涉实验验证该公式的正确性(只不过由于其他粒子的质量较电子大得多,从而粒子的能量及动量也要大得多,其物质波的波长要短得多而频率也要大得多,因此相应的实验实施难度较大),由此可见,物质波的双缝干涉现象具有普遍意义,而由于物质波的双缝干涉是物质波的叠加原理的具体体现,因此,物质波的双缝干涉现象的存在进一步证明物质波的叠加原理的正确性,同时也证明物质波概念的正确性。
4.2.2. 物质波的衍射
除了通过双狭缝后会产生干涉现象外,当物质波在传播过程中遇到障碍物、小孔或狭缝等对象时并不遵循波的直线传播规律,而是会产生通过这些对象的边缘绕到其后面继续传播的所谓衍射(或绕射)现象,而当物质波的波长与障碍物、小孔或狭缝的尺度相当或比之更大时,衍射现象会更明显,其中最典型的就是单缝(多缝)或单孔(多孔)衍射。1927年,J·戴维孙(C. Davisson)和L·革末(L. Germer)为证明德布罗意的物质波理论的正确性,利用镍单晶中镍原子构成的晶格的尺寸与电子的物质波的波长在同一数量级上的特点完成了电子的物质波的晶格(多孔)衍射实验。下面对镍单晶对电子的衍射实验的分析表明,电子的晶格衍射现象是物质波的叠加原理的具体体现,其根本原因就是物质波的叠加原理,下面进行简单分析。
图2为镍单晶的电子衍射实验的示意图,图中整齐排列的小黑点代表镍原子,众多小点按图中所示有规则的排列成的集合体则构成一种天然的镍单晶格,当电子以与镍单晶表面呈θ角的方向射向镍单晶时,被相邻两层晶格的镍原子反射的电子的物质波就会因行程上的差异而导致其复振幅的相消或相长。图中由电子枪(已省略)发射出一束平行电子束(其速度V为恒定值),当电子及其物质波ψ通过镍晶体并打到镍原子上时会被镍原子反射出去,根据物质波的叠加原理,如果被相邻两层镍晶体原子反射的电子的物质波ψ1及ψ2的行程差 (其中d为镍原子之间的距离,θ为电子束相对于镍晶体表面的入射角,λ为入射电子的物质波的波长, )时,ψ1及ψ2的复振幅为“波峰与波峰”或“波谷与波谷”叠加,相应的电子束如果垂直射到成像屏上后会产生亮点(或亮条纹);而当成像屏的位置及角度发生改变后,成像屏就会接收到来自从不同角度被镍原子反射出来的电子及其物质波ψ1及ψ2,由于角度θ发生了改变,因而电子的物质波ψ1及ψ2的行程差2dsinθ就会发生相应改变,当 时,ψ1及ψ2的复振幅为“波峰与波谷”或“波谷与波峰”叠加,相应的电子束如果垂直射到成像屏上后会产生暗点(或暗条纹)。戴维孙和革末所完成的类似实验(具体实现方法有所不同的)类似实验完全证明了以上分析的正确性,同时也证明了物质波概念及物质波的叠加原理的正确性。
另外,由于物质波通过单狭缝或单孔时也会发生衍射现象,而大约几个原子厚度的超薄金属片因原子间的非紧密排列而形成天然的小孔,因此,还可以利用电子束透射超薄金属片的实验来验证电子的物质波的衍射现象。相关实验是由英国物理学家G·汤姆逊(G. Thomson)于1927年完成的,该实验用一窄束阴极射线(能量为20~60 keV)打在金属薄箔(厚度在10−6 cm量级),在薄箔后面垂直于入射电子束方向放置照相胶片接收电子,显影后照相底片上得到了德拜–谢勒衍射环;然后再根据试验用金属薄箔的晶格结构的数据计算出了电子的物质波的波长,从而证明了德布罗意关系式及物质波概念、物质波的叠加原理的正确性 [5] ,由于采用物质波概念及叠加原理对该实验的具体分析方法与X射线的金属薄箔的衍射实验分析完全类似,并且X射线的衍射实验的定量分析许多文献中都有介绍,在此就不加赘述。除证明电子的物质波遇到狭缝或孔洞可以发生衍射现象外,在中子、原子及分子等相关实验中物理学家都观察到了衍射现象,特别是1999年维也纳大学的塞林格(Zeilinger)小组利用超大分子C60 (即富勒烯,其质量约为电子质量的130万倍)所做的相关实验,也成功观察到了衍射现象。实验从温度约1000 K的高温炉中发射出高纯度C60分子束,射入宽度为10 μm的狭缝,运动1.04 m后再次射入第二个宽度为10 μm狭缝。然后通过一个周期为100 nm、缝宽50 nm的衍射光栅,并最终在光栅后1.25 m处的探测器中形成了衍射图样 [6] 。该实验同样可以用物质波的叠加原理进行计算分析,并且相应的结论必定与实验结果完全相符,从而进一步证明了物质波概念及物质波的叠加原理的正确性及普遍适用性。
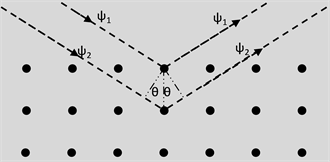
Figure 2. Experimental diagram of electron nickel crystal diffraction
图2. 电子的镍晶体衍射实验示意图
5. 物质波的波动方程
任何波除了遵循波的叠加原理之外,还遵循特定的波动方程所描述的规律,物质波也不例外,下面将对物质波的波动方程——关于描述物质波的波函数 的偏微分方程——的建立进行较详细的讨论。由于具有量子化能量的物质波是不同于经典物理学中的任何实物波的虚波,因此其波动方程无法从经典力学的原理导出,而要通过对自由粒子——特别是运动速度远低于光速的自由粒子——物质波的波动方程结构的分析中构建出来,为此,需要先建立远低于光速运动的自由粒子的物质波的波动方程。将表达式(7)两边对时间参数求偏导数,可得
(16)
再将表达式(7)两边分别对空间坐标x、y、z求两次偏导数并将所获三个等式两边分别相加,可得如下偏微分方程
(17)
上式中由于 ,则 。而在运动速度远低于光速的条件下自由粒子有如下能量–动量关系式
(18)
因而
(19)
式中 是波函数 的梯度算符,方程式(19)就是运动速度远低于光速条件下的自由粒子的物质波的波动方程。
实际上,在上述自由粒子的物质波的波动方程建立过程中,仅在通过对表达式(7)两边分别就时间、空间坐标求一次偏导数时就可得到如下具有普遍意义的关系式
(20)
(21)
如果将以上两式中波函数 对时间及空间坐标的偏导数运算看作两者之间的乘法运算,则可得到关
于波函数 的两个重要算符 及 (其中劈形算符 为梯度算符)。比较以上两个等式左右两边的运算式可见,物质波波函数 的这两个算符分别与其粒子的能量及动量密切关联,从而可以构造出波函数的所谓能量算符 及动量算符 ,使得物质波的能量(或动量)算符与物质波波函数 之间的“乘积”完全等效于其粒子的能量(或动量)与物质波波函数 之间的乘积,从而体现了物质波与其粒子之间密不可分的整体关系,也反映了物质波的虚波特征。
显然,如果将低速运动情况下自由粒子的能量–动量关系式中的粒子的能量E及动量p分别用波函数 的能量算符 及动量算符 代替,并将其作用于波函数 上,即可得到自由粒子的物质波的波动方程。同样的,利用波函数 的能量算符及动量算符,可以很自然的将运动速度远低于光速的自由粒子的物质波的波动方程推广至运动速度远低于光速且处于势场中的粒子的情况。如果运动速度远低于光速且处于势场中的粒子所具有的势能为U(r),则其能量–动量关系式为
(22)
将该等式中的能量E、动量p及势能U(r)分别用波函数 的能量算符 、动量算符 、势能算符U(r)替代,并将等式两边同乘以波函数 ,则可得
(23)
此即在低速运动情况下处于势场U(r)中的粒子的物质波的波动方程,同时也是量子力学中最基本及最重要的方程——薛定谔方程。
以上所得物质波的波动方程(即薛定谔方程)显然只适用于粒子的运动速度远低于光速的情况,而当粒子的运动速度与光速相比无法忽略时,薛定谔方程对微观现象的描述显然就会与实际完全不符,这种情况下就必须建立具有洛伦兹变换不变性的物质波的波动方程。实际上对自由粒子而言,具有洛伦兹变换不变性的物质波的波动方程有两种形式,并且这两种形式的波动方程都可以从狭义相对论中的能量–动量关系及方程对时间、空间坐标的对称性要求出发并借助波函数 的能量算符 及动量算符 而获得,二者分别是克莱因–高登方程(适用于对自旋为0的粒子如π介子等的描述)及狄拉克相对论方程(适用于对自旋不为0的费米子如电子等的描述)。对于接近光速运动的自由粒子,其能量及动量之间有关系
 (5a)
(5a)
将等式(5a)中粒子的能量及动量分别用波函数 的能量算符及动量算符替代后可得
(24)
此即克莱因–高登方程,这是波函数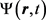 关于时间及空间的二阶偏微分方程,也是物质波的波动方程的其中一种形式,该方程显然符合洛伦兹变换不变性。若要导出以接近光速运动的自由粒子的物质波的波函数
关于时间及空间的一阶偏微分方程,则应考虑自由粒子的能量E、动量p之间的如下关系
关于时间及空间的二阶偏微分方程,也是物质波的波动方程的其中一种形式,该方程显然符合洛伦兹变换不变性。若要导出以接近光速运动的自由粒子的物质波的波函数
关于时间及空间的一阶偏微分方程,则应考虑自由粒子的能量E、动量p之间的如下关系
(25)
由于该等式两边量纲必须相同,因而右边开平方后的关系式中只能有pC项及m0C2项,将该式中粒子的能量E及动量p分别用波函数 的能量算符及动量算符替代后,要确保所得波函数 关于时间及空间的一阶偏微分方程满足洛伦兹变换不变性,方程必须具有如下形式
(26)
其中 及 分别为矩阵 为
泡利矩阵,I则是二阶单位矩阵。由此可得
, , ,
此即著名的狄拉克相对论方程。该方程是关于自由粒子的波函数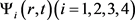 的齐次线性方程组,也是以接近光速运动的自由粒子的物质波的一阶偏微分形式的波动方程。
的齐次线性方程组,也是以接近光速运动的自由粒子的物质波的一阶偏微分形式的波动方程。
以上所述物质波的各种形式的波动方程是物质波的粒子在不同的速度条件下的具体表现形式,并且这些方程与量子力学中相应的方程数学形式完全相同,因此可以将现有量子力学的数学演算体系移植到新概念物质波的概念体系下。在现有的量子力学理论体系中,这些方程并不描述客观实在的过程,因此没有明确的物理意义,甚至在哥本哈根学派看来这些方程仅是将环境条件与测量结果联系起来的符号体系,而新概念物质波则赋予这些方程以客观意义,并使其成为可理解的。
6. 粒子的运动规律
前面我们详细讨论了物质波的存在形式及遵循的规律,而由于任何粒子都是其物质波的量子化的能量,都与其物质波之间构成密不可分的整体,因而粒子的运动必然要受其物质波的具体形状的制约并由物质波的传播方式决定。波之所以能以其特有的形式表现出来,完全由其能量分布规律——波在其波场的任一点上的强度与波在该点上的振幅的平方成正比——所决定,因而波的能量分布规律同样是所有波都必须遵循的规律。但由于物质波是虚波,其波场的所有振动着的微元都不具有能量,因而,波的能量分布规律无法在物质波上直接表现出来,而是必须且只能通过其(量子化的能量)粒子在物质波的波场中任一点上出现的概率间接表现出来,而粒子的力学量的概率分布就是由此产生的;另外由于物质波是客观存在的虚波且其量子化的能量由其粒子所携带,因此当物质波的粒子与环境发生作用致其能量及动量发生改变时,物质波的形状也必然发生瞬间变化乃至塌缩,由于物质波的自然塌缩及其作用的客观实在性,薛定谔猫悖论及EPR悖论都可以得到合理解释;再者由于粒子是其物质波的量子化的能量,因此若将粒子的某一力学量限制在一定范围内并对其进行测量时,因粒子的物质波的作用,这种测量必然对与该力学量构成非对易关系的另一力学量的量值造成扰动并使之变得更加不确定,粒子的非对易关系的力学量之间的测不准关系可以由此得以表现,下面进行较详细的论述。
6.1. 粒子的力学量的概率分布
这里主要讨论粒子的空间坐标的概率分布,粒子的其他力学量的概率分布与量子力学中的结论基本相同,所不同的只是其物理含义,在此就不赘述。在讨论问题之前先回顾一下波的能流密度的概念,所谓波的能流密度是指波在传播过程中于单位时间内通过垂直于其传播方向上的单位面积的能量,并且波在其波场的任一空间坐标上的能流密度与波在该坐标上的振幅的平方成正比,而能流密度越大就意味着波的强度越强,因此能流密度也用于表示波的强度,也就是说波在其波场的任一空间坐标上的强度与波在该坐标上的振幅的平方成正比。由于物质波是一种特殊的波——虚波,因而波的强度概念同样也适用于物质波但又与上述波的强度概念有所不同,即物质波在其波场的任一空–时坐标 上的强度I与物质波在该坐标上的振幅 的模的平方成正比,即 。同时由于任何一列物质波的能量都是量子化的、全部由其微观尺度的一个粒子携带并且该能量属于整列物质波,因而物质波的粒子不可能只出现在其波场的某些特殊的空–时坐标上而是在物质波的波场的所有空–时坐标上都有出现的可能性(此即粒子的物理量具有概率分布特征的根源),并且物质波在其波场的任一空–时坐标上的强度越大,就意味着粒子在该空–时坐标上出现的频次就越多、发现该粒子的概率就越大;反之粒子在该空–时坐标上出现的频次越少、发现该粒子的概率越小。如在上述电子的物质波的双缝干涉现象中,如果电子枪以极高的强度发射电子流,则电子及其物质波在通过双缝并最终投射到成像屏上时在电子的物质波的理论计算强度为极大值处会很快出现亮条纹,而在成像屏上电子的物质波的理论计算强度为极小值处则为暗条纹;如果电子枪以极弱的强度持续的、一颗一颗的发射电子,则刚开始时电子及其物质波通过双缝并最终投射到成像屏时形成的亮点是不规则的、完全散乱的,但随着时间的流逝,在成像屏上电子的物质波的理论计算强度为极大值处聚集的亮点逐渐增多并最终形成明亮条纹,而在成像屏上电子的物质波的理论计算强度为极小值处则很少有亮点出现并最终显示暗黑条纹,该实验用两种不同的方式直观证明了物质波在空间中某一点上的强度与物质波的粒子在该点上出现的概率成正比这一重要结论。
综上所述可以获得结论:如果描述物质波的波函数为 ,则物质波在其波场的任一空–时坐标 上的振幅的模的平方 与物质波在该坐标上的强度I成正比,并且物质波在空–时坐标 上的强度I与在该点上发现粒子的概率成正比。因此,波函数为 的物质波在其波场中任一空–时坐标上的振幅的模的平方 与在该点上发现粒子的概率成正比。
若用 表示在时刻t于空间坐标 附近无穷小邻域 内发现粒子的概率,则
(27)
其中 为空间坐标 的长为dx、宽为dy、高为dz的无限小邻域的体积,K为比例常数。若将在时刻t于物质波的空间坐标 附近单位体积内发现粒子的概率定义为概率密度 ,则
(28)
若将dW进行全域积分,则可得到粒子在整个无限三维空间中出现的概率,并且由于粒子只能且必须存在于三维空间中,因而粒子在三维空间中出现的概率为1,从而有
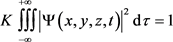 (29)
(29)
显然
(30)
若令 ,则有
(31)
并称波函数 为归一化波函数。
以上用物质波的概念直观诠释了描述物质波的波函数的统计意义,从而揭示了量子力学中所谓概率波背后真正的物理机制并将波函数的统计解释建立在了波函数所描述的物质波是客观存在的这一假设基础之上,这就意味着波函数的统计解释必须在其物质波概念(而非纯粹主观意义上的概率波)基础之上才能得到真正理解。
6.2. 粒子的力学量的测量与薛定谔猫悖论及EPR悖论
由于物质波Ψ(r)是客观存在的虚波且其量子化的能量由其粒子所携带,因而当物质波Ψ(r)的粒子由于同环境因素发生相互作用而导致其能量E及动量p的量值发生改变时,由德布罗意关系式(
、
)可知物质波Ψ(r)的形状(由其角频率ω及波数k决定)也必然发生相应的瞬间变化,并且相应的变化速度不受光速限制(理论上为无限大),因而该过程无法用数学描述;特别是当粒子被宏观物体吸收或俘获时其动量及能量必然会发生突变(理论上如此,实际上变化是连续的),而粒子的物质波Ψ(r)则瞬间收缩至粒子被吸收或俘获的空间区域(而除此之外的空间区域找到该粒子的概率即刻变为零),我们称物质波Ψ(r)的这种突变为塌缩,且塌缩多为不可逆的;如单色平面光波的量子化的能量——光子——投射到发光屏上并被吸收后可以认为光子消失了(即光子的能量及动量都为零,则由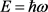 、
可知光波的角频率ω及波数k均为0),这时光波从单色平面形式自然塌缩至发光屏上的一点上;又如,自由电子的物质波是单色平面物质波,当电子经过原子核附近时被原子核俘获,则电子的物质波由单色平面波形式自然塌缩至原子核附近的微小区域中(在该区域内电子的物质波的具体形状可由薛定谔方程求得)。由此可见,任何物质波的塌缩都是自然发生的,不需要人的参与及确认。而当物质波Ψ(r)的形状发生改变时其粒子的能量及动量也会随之而变化:如当单色平面物质波Ψ(r)通过单狭缝后因单缝衍射导致其形状发生了改变,这时物质波Ψ(r)的粒子的动量也会变得不确定;又如当单色平面光波被截断为一个有限长度的波段时,位于该波段中的光子的能量将成为不确定的。总之,粒子的能量及动量的变化改变其物质波的形状,物质波形状的变化则改变其粒子的各力学量算符的本征值及其在任一微小空间区域上出现的几率。而量子力学中所说的测量导致的波函数Ψ(r)随机地塌缩至其粒子的某个本征态的本质就是粒子被测量仪器俘获或吸收的瞬间其物质波的塌缩,因而测量会导致物质波的塌缩但并非导致物质波塌缩的唯一原因,并且在目前量子力学中具有重要意义的测量概念对新的物质波概念而言并没有特别意义。显然,关于物质波的粒子的力学量的测量原理的表述与量子力学中基本一致,只不过需要将量子力学相关表述中的波函数改为物质波的波函数,并且原理中物质波的塌缩是自然发生的而非人的观测所导致,在此就不赘述。由于在现有的量子力学体系中“波函数不代表真实的物质波而是主观意义上的概率波”,因此,波函数的塌缩必须由人参与并经人的观察确认后才能发生,由此导致了薛定谔猫悖论及EPR悖论,并且对这两个悖论意义的争论至今仍在持续,下面我们将借助新的物质波概念进行分析。
、
可知光波的角频率ω及波数k均为0),这时光波从单色平面形式自然塌缩至发光屏上的一点上;又如,自由电子的物质波是单色平面物质波,当电子经过原子核附近时被原子核俘获,则电子的物质波由单色平面波形式自然塌缩至原子核附近的微小区域中(在该区域内电子的物质波的具体形状可由薛定谔方程求得)。由此可见,任何物质波的塌缩都是自然发生的,不需要人的参与及确认。而当物质波Ψ(r)的形状发生改变时其粒子的能量及动量也会随之而变化:如当单色平面物质波Ψ(r)通过单狭缝后因单缝衍射导致其形状发生了改变,这时物质波Ψ(r)的粒子的动量也会变得不确定;又如当单色平面光波被截断为一个有限长度的波段时,位于该波段中的光子的能量将成为不确定的。总之,粒子的能量及动量的变化改变其物质波的形状,物质波形状的变化则改变其粒子的各力学量算符的本征值及其在任一微小空间区域上出现的几率。而量子力学中所说的测量导致的波函数Ψ(r)随机地塌缩至其粒子的某个本征态的本质就是粒子被测量仪器俘获或吸收的瞬间其物质波的塌缩,因而测量会导致物质波的塌缩但并非导致物质波塌缩的唯一原因,并且在目前量子力学中具有重要意义的测量概念对新的物质波概念而言并没有特别意义。显然,关于物质波的粒子的力学量的测量原理的表述与量子力学中基本一致,只不过需要将量子力学相关表述中的波函数改为物质波的波函数,并且原理中物质波的塌缩是自然发生的而非人的观测所导致,在此就不赘述。由于在现有的量子力学体系中“波函数不代表真实的物质波而是主观意义上的概率波”,因此,波函数的塌缩必须由人参与并经人的观察确认后才能发生,由此导致了薛定谔猫悖论及EPR悖论,并且对这两个悖论意义的争论至今仍在持续,下面我们将借助新的物质波概念进行分析。
6.2.1. 薛定谔猫悖论分析
为证明量子力学的理论体系是不完备的,奥地利物理学家薛定谔于1935年提出了将猫置于既活又死叠加态的著名理想实验,该理想实验的设施有:在实验箱里的一只健康的猫、一瓶氰化钾溶液、少量放射性物质、悬挂在氰化钾溶液瓶上方的铁锤以及能够接收到放射性物质的衰变信号并由此触发铁锤下落的触发装置。显然,放射性物质有50%的概率衰变并触发铁锤下落而后击碎氰化钾溶液瓶从而释放出毒气杀死这只猫;同时,放射性物质有50%的概率不衰变而猫将存活下来。根据经典物理学,在未打开实验箱时猫只能处于或者活或者死这两个状态之一,外部观测者打开实验箱后就能确定实际情况。由于在量子力学中波函数不代表真实的物质波而是主观意义上的概率波,从而在认识层面上将微观现象的不确定性与宏观物体的状态耦合了起来,因此在未打开实验箱时整个系统的状态相对于观测者而言始终是不确定的,从而猫处于既活又死的叠加态。只有当实验箱打开后并经外部观测者观测时,猫的这种既活又死的状态才能塌缩至活猫态或死猫态。这项实验旨在演示量子力学对微观粒子世界超乎常理的认识和理解,并使微观不确定原理演绎为宏观不确定原理,但常识告诉我们,没有任何人见过既活又死的猫,而量子力学却推论出这种状态的猫的存在,显然违背了常识从而导致了悖论的产生,这就是著名的薛定谔猫悖论。
由以上分析可见,导致薛定谔猫悖论的根源在于分析过程中应用了哥本哈根提出的“波函数不代表真实的物质波而是主观意义上的概率波”的观点,因此试验中猫的既活又死的这种人的主观意义上的叠加态必须经由人观测确认后才能塌缩至活猫态或死猫态,而用新的物质波概念对薛定谔猫实验进行分析则能够消除其中的悖论。在分析前我们将实验进行等效调整,用一套由1秒钟发射一次且每次只能发射一个光子的光子枪及一块50%的半透镜构成的装置代替其中的放射性物质,其中只有穿过半透镜的光子才能被信号检测装置检测到并触发铁锤下落击碎氰化钾溶液瓶从而即刻(假定不需要时间)毒死猫,而被半透镜反射至另一方向上的屏幕上光子则无法触发铁锤下落,从而猫处于活的状态。1秒钟后当一个光子与其物质波以与半透镜呈45˚角方向射向半透镜时其物质波Ψ0分成两部分,即透过半透镜的物质波Ψ1及被半透镜反射的物质波Ψ2。显然,这两列物质波分别对应于光子的两个本征态ψ1及ψ2,并且还分别与宏观意义上猫的死态ψ死及活态ψ活相对应,因而有 。如果光子穿过半透镜从而触发信号装置时,其物质波Ψ0即刻自然塌缩至其光子的本征态ψ1,与此同时光子显然不可能再处于其本征态ψ2,从而猫必将即刻死去;而如果光子被半透镜反射至另一方向上的屏幕上,则物质波即刻自然塌缩至其光子的本征态ψ2,与此同时光子显然不可能再处于其本征态ψ1,从而猫必将活着;而在物质波没有塌缩时其光子显然没有触发信号装置,猫不可能处于死态ψ死从而必将活着。由以上分析可见,从光子枪发射出的光子必须在其物质波自然塌缩时才能与猫的死态ψ死及活态ψ活发生耦合关系从而决定猫究竟是死去还是活着,这与量子力学中一开始就将微观现象的不确定性与宏观物体的状态耦合起来的分析方法完全不同。显然,在实验过程中猫要么活着要么死去,不可能有既活又死的猫的叠加态存在,并且猫究竟是活是死根本不需要人的主观意识的确认,薛定谔猫所处状态完全由光子的物质波的自然塌缩所决定。可见,用新的物质波概念对薛定谔猫实验的分析可以完全避免悖论的出现。
6.2.2. EPR悖论分析
1951年,D·玻姆提出了玻姆版本的EPR悖论,又称为“EPRB悖论”,该版本悖论所涉及的实验是助施特恩–格拉赫仪器测量粒子沿z轴方向的离散自旋。假设一个0自旋的中性π介子衰变成一个电子与一个正电子,这两个衰变产物各自朝相反方向运动。当电子运动至空间坐标A时该点上的观察者a将观测到电子沿z轴方向的自旋;而当正电子运动到空间坐标B时该点上的观察者b将观测到正电子沿z轴方向的自旋。这两个纠缠粒子共同形成零自旋单态,是两个直积态的叠加。若不做测量,则无法知道这两个粒子中任何一个粒子沿z轴的自旋,并且根据哥本哈根诠释,这个变量并不存在。这个单态具有旋转不变性,对于任意取向的参考轴,它保持同样的性质。这个单态的两个粒子相互反关联,测量沿着z轴的自旋,假若电子自旋为+1/2,则正电子自旋为−1/2,假若电子自旋为−1/2,则正电子自旋为+1/2。量子力学不能预测到底是哪一组数值,但可以预测获得任何一组数值的概率为50%,对这种情况,物理学家称电子与正电子处于量子纠缠态。
局域性原理表明,任何物体只能直接被相邻区域发生的事件所影响,遥远区域发生的事件必须以某种不超过光速的传递方式间接影响该物体,因为根据狭义相对论,信息传播的速度不会超过光速,否则将违背因果律从而造成逻辑悖论并使该理论无法成立。而物理学家经论证发现,量子力学的描述虽然违反局域性原理(如波函数的塌缩就具有非局域性),但并不违背因果律,并且量子态不可能以有限速度塌缩,否则将违反角动量守恒定律。由于违反局域性原理,因而爱因斯坦将非局域性量子行为嘲讽为“鬼魅般的超距作用”,这是他不相信量子力学的主要原因之一,他认为物理理论不应该允许超距作用存在;而在哥本哈根学派看来,量子力学的非局域性行为意味着在某种状况下狭义相对论可能需要修正。虽然迄今为止一系列精密实验支持了量子力学的正统解释,但EPR悖论所揭示的量子力学的深层次问题依然存在,特别是对处于纠缠态中的粒子之间究竟存在一种什么性质的关联或相互作用这一问题,目前的量子力学理论依然无法回答。
下面我们将使用建立在新概念物质波基础上的量子力学对其进行简单分析,通过分析可以解决以上问题。设有一自旋为0的静止中性π介子衰变为一个电子A及一个正电子B,则系统的态(即描述电子A-正电子B纠缠系统的两分量的列旋量物质波的波函数)为:
(32)
式中 、 及 、 分别为自旋沿z轴方向的电子A及正电子B的自旋算符的本征态。这是一个自旋为(0)单态的电子–正电子纠缠态,因而在任一时刻电子A及正电子B的自旋都在各自的不同本征值之间不断自发发生同步跃迁,即当电子A的自旋自发跃迁至其本征值+1/2时,正电子B的自旋则即刻(绝对意义上的同时)自发跃迁至其本征值−1/2;而当电子A的自旋自发跃迁至其本征值−1/2时,正电子B的自旋则即刻自发跃迁至其本征值+1/2,并且发现电子A及正电子B的自旋为本征值+1/2或−1/2的概率均为50%,从而电子A及正电子B的自旋在任一时刻都是不确定的。如果要对电子A沿z轴方向的自旋进行测量,则根据建立在新概念物质波基础上(基于物质波的叠加原理)的测量公设,系统的物质波 可以按(32)式描述的被测量算符的本征态展开。由于该电子A-正电子B纠缠态的总自旋为0,因而如果实施测量时物质波 塌缩至其电子A的本征态 ,则物质波 (在绝对意义上)同时也自然塌缩至其正电子B的本征态 ;而如果实施测量时物质波 塌缩至其电子A的本征态 ,则物质波 (在绝对意义上)同时也自然塌缩至其正电子B的本征态 。由以上分析可知,两个或多个粒子之间必须且只能通过系统的物质波 这一中介才能产生纠缠关联,并且在对电子A沿z轴方向的自旋进行测量时导致描述系统的态的波函数 塌缩的本质就是用波函数描述的系统的物质波 的自然塌缩;由于物质波是振幅为复数的虚波且与其粒子永远相生相伴、构成不可分割的整体,因而处于纠缠态的粒子之间即便相距光年之遥,系统的物质波的作用永远也不会减弱(由于虚波无所谓强弱,因而量子纠缠不受纠缠粒子之间空间距离影响这一特性印证了新的物质波概念的正确性),也就是说处于纠缠态的粒子之间并不存在所谓的超距作用,而正是由于物质波的存在才使得处于纠缠态的粒子之间成为了一个整体并由此产生了纠缠关联。对粒子的量子纠缠现象而言,物质波的存在至关重要,可以说如果没有物质波,粒子之间就不可能产生量子纠缠;而如果没有全新的物质波概念,量子纠缠及量子纠缠中所谓的超距作用都无法理解,而量子纠缠现象的存在证明了新的物质波概念的正确性。
6.3. 粒子的非对易力学量之间的测不准关系
测不准关系是微观粒子的力学量之间最基本的关系,是物质波存在并起作用的必然结果。粒子的动量与其空间坐标之间的测不准关系最早由德国物理学家海森堡于1927年提出并证明,其表达式为
(33)
其意义是在任何情况下粒子的空间坐标与其在该坐标方向上的动量都无法同时精确测量,两者的测量偏差的乘积的下限为普朗克常数 的二分之一,该下限无法通过对实验的控制及预测进行修正或抵消。下面就如图3所示的电子的物质波的单缝衍射实验的情况进行分析。
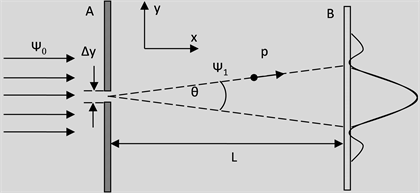
Figure 3. Experimental diagram of single slit diffraction of electrons
图3. 电子的单缝衍射实验示意图
为测量电子在y轴方向上的坐标,在图3中平板A上刻有一条宽度为Δy的单狭缝,平板A与成像屏B之间距为L,现将一束速度为V的自由运动的电子(其物质波是波长为λ的单色平面波)射向平板A。对通过狭缝的电子,其在y轴方向上的位置的不确定度显然为Δy,由于当电子通过狭缝时其物质波也通过狭缝并且发生衍射现象,因而电子在成像屏上的落点位于其物质波的衍射条纹上并且其位置显然是不确定的,而此时电子在y轴方向上的动量py同样也不确定。如果成像屏上最大亮条纹到其第一条暗条纹之间的宽度为H,则根据单缝衍射计算可知,平板A的狭缝到该衍射亮条纹之间构成的最小张角θ符合公式 ,当Δy远大于λ时, ,则有 。显然,平板A上的单狭缝宽度Δy越大,则θ越小,落在成像屏上的电子的动量py的不确定度也越小;而如果单狭缝宽度Δy越小,则θ越大,落在成像屏上的电子的动量py的不确定度也越大;特别的,由于电子在通过单狭缝之前是自由粒子,其动量为恒定值,即 ,而此时电子在y轴方向上的坐标则完全无法测定;当电子通过狭缝后,其物质波的空间形状发了改变,从而导致其电子的动量(当然包括其动量py)也发生相应的改变,从图中可见,电子的动量p在y轴方向上发生改变的量值(即电子的动量在y轴方向上的不确定度) ,因而有 ,以上只是简单分析,更精确的分析则可得其下限为 。
此外,我们还可以用物质波概念对其他相关的、用于测量粒子的空间坐标及在该坐标方向上的动量的实验(如海森堡本人提出的借助显微镜的观测来确定电子的位置与动量的理想实验、测定原子核外“电子云中”电子的动量等实验)进行分析,所得结论都将与海森堡测不准关系完全相符,其本质就是前面提到过的用粒子的空间坐标表示的物质波的波函数 与用粒子的动量表示的物质波的波函数 之间互为傅里叶变换式(从而粒子的空间坐标与动量两者间构成所谓的非对易关系),而这显然是物质波的叠加原理的具体表现形式。因而关于海森堡测不准关系的证明还可以利用粒子的坐标x (或y、z)与动量px (py、pz)的测量均方根偏差获得,即
(34)
(35)
利用傅里叶变换的带宽定理,就可得到海森堡测不准关系 [7]
(33a)
实际上,对物质波的粒子而言,不仅其动量与坐标之间存在测不准关系,而且其乘积的量纲等于作用量 的量纲的两个(其算符具有非对易关系的)力学量之间都存在测不准关系,如粒子的能量与时间之间的测不准关系
(36)
又如在粒子的角动量Lz的本征态Ylm中, ,这种情况下该粒子的另外两个角动量Lx与Ly之间也存在测不准关系
(37)
可见测不准关系是微观粒子的各种力学量中具有普遍意义的关系。因为量子力学中的粒子的两个具有非对易关系的力学量之间的测不准关系是波函数所描述的物质波的叠加原理的具体表现形式,所以测不准关系完全可以由物质波概念出发推导出来,如各种文献中提到的关于测不准关系的更一般的证明就是利用描述物质波的波函数的算符及其运算实现的 [8] ,由于篇幅所限就不赘述。总之,测不准关系既可作为物质波是客观存在而其作用是客观实在的重要证据,同时也是微观粒子完全不同于宏观物体运动过程的本质特征。
7. 物质波存在的实验验证
物质波虽然是虚波,但却是客观存在的而其作用则是客观实在的,并且各种量子力学文献中列举的所有关于微观粒子的双缝干涉及单缝衍射等实验本质上都是关于物质波客观存在并起作用的证据。虽然由于历史的原因,最早由德布罗意提出并导致物理学重大变革的d-物质波概念最终被玻恩的概率波概念所替代(其主要原因是概率波概念与所谓粒子的波动性实验的数据相吻合而德布罗意的d-物质波概念则无法做的更好,仅此而已),但物质波的存在并没有被任何量子力学的相关实验所否定,甚至物理学史上连相关的物理学实验都没实施过,反倒是任何一个关于粒子的波粒二象性的物理学实验或现象都在反复验证着物质波的存在及对粒子的作用。当然,由于物质波是虚波,无法通过观测物质波与探测仪器之间相互作用的方式直接证明其存在,因此,之前量子力学的各种文献中所涉及的所有关于所谓粒子的波粒二象性实验(如粒子的双缝干涉及单缝衍射现象、量子隧道效应、电子显微镜观察到的铁原子环形围栏内同心圆柱状驻波 [9] 乃至量子纠缠现象等)都只间接(而非直接)证明了物质波的存在。
虽然如此,但仍然可以借助专门设计的实验来验证物质波的存在及其作用。清华大学教授龙桂鲁先生就于2018年实施了一项与此相关的实验,该成果发表在Science China Physics, Mechanics & Astronomy (《中国科学:物理学,力学,天文学》) 2018年第3期的英文版上,相关研究论文标题为“Realistic Interpretation of Quantum Mechanics and Encounter-Delayed-Choice Experiment”,该论文由龙桂鲁教授担任第一和通讯作者撰写 [10] 。在论文中,龙桂鲁教授认为描述微观物体的波函数就是微观物体的真实存在,而不再仅仅是一种简单的数学描述手段,也就是说,微观物体是以波函数的形式存在的。为了支持波函数的这一实在论诠释,龙桂鲁教授与合作者们设计并实现了一种巧妙的相遇延迟选择实验,根据波函数的实在论诠释,Mach-Zehnder干涉仪入口处的50:50分束器会将入射单光子的波函数分成分别沿干涉仪两臂同时传播的子波函数。一段时间之后,这两路子波函数会在干涉仪的出口处相遇。此时,若在出口处也放入一个50:50的分束器(如图4(a)所示),那么没有经过分束器的两路子波函数就不会发生干涉,表现粒子性。相反地,经过分束器的两路子波函数却会发生干涉,表现为波动性,单光子的波函数也即空间存在形式因而发生改变(如图4(b)所示)。该实验最终获得的实验数据很好地符合了波函数的实在论诠释并有力地支持了研究者的观点 [2] ,因此,该实验结论同样也为本文提出的用波函数描述的物质波是客观存在的而其作用是客观实在的这一观点提供了强有力的支持,同时还从根本上否定了哥本哈根学派关于“波函数不是客观存在的物质波而只是主观意义上的概率波”的观点。
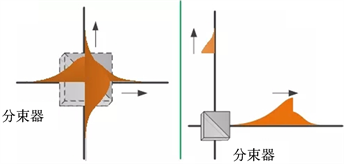 (a) (b)
(a) (b)
Figure 4. (a) Indicates that when the two-way wave function meets at the interferometer exit, the beam splitter is placed; (b) Indicates changes in the spatial morphology of a single photon due to interference by a subwave function caused by a beam splitter
图4. (a) 表示当两路子波函数在干涉仪出口相遇时放入分束器;(b) 表示单光子空间形态因分束器导致的子波函数干涉而引起的变化
为进一步证明物质波概念的正确性,本文也设计了一项实验,其实验装置如图5所示。图中E为量子纠缠光子对产生–发射装置,可确保每一次都能同时向左右相反方向一对一对地发射量子纠缠光子对,D1、D2为光子探测仪,S1为半(50:50)透镜,S2为全透镜,R为全反射镜,线段a + c = b + d = a + a1,a = b,c = d = a1。现从E发射纠缠光子对,并微调S2,使得自S1反射至S2及自R反射至S2的光子对到达S2镜面时两者的波函数 及 的相位差为90˚角,从而两者的振幅相互抵消,垂直置于S2镜面上的D2因此无法探测到光子。现从E持续的、一对一对的向左右两边发射纠缠光子对,按哥本哈根学派的解释,当D1接收到一个光子信号则没有自S1反射至S2的光子,因而从R反射至S2的光子可直接透过S2被D2所探测;而根据物质波概念,由于从E的左边发射出的光子的波函数ψ1到达S1时被分为两部分(ψ2及 ),因此即使光子本身透过S1,其波函数 仍然会经由线段c到达S2,并与自R反射至S2的光子的波函数ψ1相叠加从而两者的振幅相互抵消,此时D2仍然无法探测到光子。也就是说,如果当D1探测到从E左侧发射的光子时D2也能探测到从E的右侧发射出来的光子,说明哥本哈根学派的诠释是正确的;而如果D1探测到从E的左侧发射出来的光子时D2无法探测到从E的右侧发射出来的光子,则证明波函数描述的物质波在试验中产生的作用是真实存在的,而这种作用显然是量子力学中作为描述工具的波函数所无法产生的,从而可以作为物质波概念正确性的一个佐证。该实验实施难度不很大,但确保E中每一次向左右相反方向发射的都是光子对则是实验的关键,实验改进后还可以作为用电子及其他粒子为实验对象证明物质波概念正确性的佐证,相信与清华大学龙桂鲁教授的实验结果一样,本实验的实施也将有力支持本文提出的物质波概念。
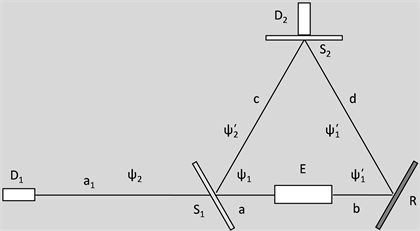
Figure 5. An experimental diagram of the existence of the object described by the photon wave function
图5. 光子的波函数描述的对象的存在性实验示意图
8. 结论
由于波函数描述的是客观存在的物质波而非主观意义上的概率波,因而为揭示物质波的存在形式及其各种属性,本文在d-物质波概念基础上,通过与爱因斯坦光量子理论的类比,提出任何一列物质波的能量都是量子化的、与之相伴随的粒子就是其量子化的能量的假设,并在此基础上通过对物质波存在形式的详细分析发现任何一列物质波都必须且只能是虚波,从而物质波的波振幅无法用实数而必须要用复数描述,确切地说物质波必须且只能用量子力学中的波函数进行描述,而这正是本文提出的新概念物质波完全不同于d-物质波概念之处。而后在新概念物质波基础上经过详细分析及推理获得了以下结论:
1) 任何粒子的物质波都必须遵循物质波的叠加原理,而这正是所谓粒子的态的叠加原理的本质,并且各种粒子的双缝干涉及单缝衍射现象都是物质波的叠加原理的具体体现,同时这些现象均可在新概念物质波基础上获得真正意义上的理解;
2) 量子力学中的薛定谔方程、克莱因–高登方程及狄拉克方程等是在不同速度条件下物质波的波动方程的具体形式,这些方程均可由新概念物质波出发得以建立,从而可重建(而非简单的重复)量子力学;
3) 波函数统计解释的本质为用于描述粒子的态的波函数其描述的对象就是客观存在且其能量具有量子化特征的物质波,因而完全可以借助新概念物质波得以理解,并且薛定谔猫悖论及EPR悖论(或量子纠缠)也可以在新的物质波概念基础上得以圆满解决;
4) 粒子的任意两个具有非对易关系的力学量之间都存在的测不准关系是波函数所描述的物质波的叠加原理的具体表现形式,因而完全可以借助新概念物质波进行诠释;
5) 新概念物质波具有可证伪性,其存在已获得有关物理学实验的证实,因而是科学的概念;
6) 哥本哈根学派关于“波函数不代表真实的物质波而只是主观意义上的概率波”的观点是错误的。
综上所述,由于物质波是客观存在的、其作用是客观实在的,并且微观粒子是物质波的量子化的能量从而其运动必须要受物质波的制约,而量子力学中所谓的粒子的波粒二象性正是这种制约的直接结果,如果说没有波函数概念,就不可能建立完整的量子力学理论体系,那么可以说如果没有新概念物质波,波函数将没有存在的依据,并且建立在波函数基础之上的量子力学必将成为没有现实意义的空中楼阁,因此量子力学必须建立在具有客观意义的新概念物质波(而非具有主观色彩的概率波)基础之上才能成为完备的、可理解的理论。
致谢
在此谨向我的妻子应丽芬女士的全力支持深表感谢!同时也要由衷地感谢陈建良先生及武新贤先生的关心及帮助!另外还要感谢石河子大学的韩川博士对本文局部内容提出的一些修改意见!
文章引用
李大庆. 量子力学中的波函数与新概念物质波
Wave Functions in Quantum Mechanics and the New Concept of Matter Waves[J]. 现代物理, 2019, 09(05): 206-226. https://doi.org/10.12677/MP.2019.95023
参考文献
- 1. 李宏芳. 量子理论的观念之争和认识论发展[M]. 北京: 科学出版社, 2015: 19.
- 2. 中国科学物理辑中国科学杂志社. 相遇延迟实验和量子力学波函数的实在性本质[EB/OL]. https://mp.weixin.qq.com, 2018-01-09.
- 3. 德布罗意. 德布罗意文选[M]. 北京: 北京大学出版社, 2016: 9, 111, 140, 149.
- 4. 张永德. 量子力学[M]. 第4版. 北京: 科学出版社, 2017: 7, 323.
- 5. 朱栋培. 量子力学基础[M]. 合肥: 中国科学技术大学出版社, 2016: 9.
- 6. 顾樵. 量子力学I[M]. 北京: 科学出版社, 2018: 50.
- 7. 张永德. 量子力学[M]. 第4版. 北京: 科学出版社, 2017: 7, 13.
- 8. 朱栋培. 量子力学基础[M]. 合肥: 中国科学技术大学出版社, 2016: 137-139.
- 9. 朱栋培. 量子力学基础[M]. 合肥: 中国科学技术大学出版社, 2016: 10.
- 10. Long, G.L., Qin, W., Yang, Z. and Li, J.-L. (2018) Realistic Interpretation of Quantum Mechanics and Encounter-Delayed-Choice Experiment. Science China Physics, Mechanics & Astronomy, 61, Article ID: 030311.
https://doi.org/10.1007/s11433-018-9162-4