Applied Physics
Vol.4 No.04(2014), Article ID:13545,6 pages
DOI:10.12677/APP.2014.44007
First-Principles Investigation of Electronic Structure and Optical Properties in N-S Codoping ZnO
1Department of Electronics and Information Engineering, Huangshi Polytechnic College, Huangshi
2Key Laboratory for Optoelectronics and Communication of Jiangxi Province, Jiangxi Science & Technology Normal University, Nanchang
Email: chenlanli@126.com
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Apr. 6th, 2014; revised: Apr. 28th, 2014; accepted: May 6th, 2014
ABSTRACT
To analyze the electronic structures and optical properties of pure-ZnO and N-S codoped ZnO, the defect formation and ionization energy, density of states, conductivity, dielectric constant and adsorption coefficient of varies complexes were calculated by the first-principles calculation methods based on Density Functional Theory (DFT). It is found that 3N-S codoping in ZnO not only enhances N acceptor solubility, but also leads to shallower acceptor energy, demonstrating that 3N-S codoping can obtain a high-quality and more stable p-type ZnO. Furthermore, as the incorporation of N atoms is increasing, the ionization energies of the complexes are sharply decreasing, and the conductivity of the system is enhanced. In addition, the calculation of the dielectric functions and adsorption spectrum shows that 3N-S codoped ZnO has interesting characteristic in the low-energy region. We expect that this theory study might be helpful for the experimental results.
Keywords:Codoping, First-Principles, Conductivity, Electronic Structure, Optical Properties, ZnO

N-S共掺ZnO的电子结构和光学性质的第一性原理研究
胡宏铎1,陈兰丽1,2
1黄石职业技术学院信息工程系,黄石
2江西科技师范大学江西省通信与光电子重点实验室,南昌
Email: chenlanli@126.com
收稿日期:2014年4月6日;修回日期:2014年4月28日;录用日期:2014年5月6日

摘 要
为了分析纯净ZnO和N元素的掺入对S掺杂ZnO的电子结构和光学性质的影响,基于密度泛函理论采用第一性原理计算方法,我们研究了各种复合体的缺陷形成能、离化能、态密度、导电率、介电函数和吸收系数。结果发现:3N-S共掺ZnO不仅能提高N受主溶解度,而且可以引起浅受主能级。这表明3N-S共掺能够得到高质量稳定p型ZnO。同时,随着N原子的增加,体系的离化能迅速降低,而体系的导电率增强。另外,通过对介电函数和吸收系数的计算,结果表明3N-S共掺ZnO在低能区有非常奇特的特性。希望不久我们的理论结果能够为实验提供理论依据。
关键词
共掺,第一性原理,导电率,电子结构,光学性质,ZnO

1. 引言
由于ZnO在室温下具有3.4 eV的宽带隙和60 meV的大激子束缚能等特性,导致ZnO在电子和光学材料中得到广泛应用。因此,ZnO是继GaN后在短波长范围内半导体材料又一取代物。然而,纯净ZnO表现为n型特征,而由于自补偿作用、高离化能,以及低的溶解度,导致p-型特征的ZnO是非常难制备。因此,很多研究组采用很多不同的方法去解决这个问题。首先,很多研究组采用单掺的方法得到p型ZnO。例如:Ag[1] 和N[2] 。后来Yamamoto, T[3] 建议使用共掺的方法能够解决p型ZnO制备过程中的不同极性的问题。因此,很多小组使用不同的掺杂元素采用共掺方法实现p型ZnO,例如:N-Mg[4] ,N-B[5] ,以及N-Zr[6] 。同时,Wei等人[7] 报道N-S共掺TiO2能够得到吸收边的红移和它的高催化活性是与在紫外区强吸收合成效应有关,而且,N-S共掺能引起红移现象、氧空位的出现和表面催化。另外,Wen等人[8] 发现N-F共掺ZnO导致浅受主能级,并形成p型ZnO。然而,至今,对于N-S共掺ZnO的电子结构和光学性质的全面研究还甚少。因此,对N-S共掺对p型ZnO电学性质和光学性质的研究是非常有必要的。
2. 计算方法和计算模型
2.1. 计算方法
所有的计算工作都是基于密度泛函理论的第一性原理计算程序即在Vienna Abinit Simulation Package(VASP)[9] [10] 代码采用密度泛函理论。采用的交换关联势为广义梯度近似(GGA)。计算参数设置情况:采用网格为5 × 5 × 3的Monkorst-park特殊k点对整个布里渊区求和,平面波截断能为450 eV。所有的原子全部弛豫直到原子之间的力低于0.01 eV/Å。通过第一性原理在总能最小的情况选择最优化结构。为了得到可靠的结果,在结构优化基础上进行静态计算。
2.2. 计算模型
在本文中,构建包含32个原子的2 × 2 × 2纯净ZnO的超晶胞。三种掺杂体系分别为N-S,2N-S和3N-S复合体。各种模型如图1所示。其中:(a) 纯净ZnO;(b) N-S体系,一个N原子替代一个O原子,一个S原子替代另外的一个O原子;(c) 2N-S体系,两个N取代2个O原子,一个S原子替代另外的一个O原子;(d) 3N-S体系,3个N原子取代3个O原子,一个S取代另外的一个O原子。通过优化纯净ZnO的结构,计算得到的晶格常数为:a = 3.281 Å, b = 3.281 Å, c = 5.277 Å, c/a = 1.608,这和实验结果[2] 相吻合。各种体系的晶格常数和离化能如表1所示。
3. 结果与讨论
3.1. 缺陷形成能和离化能
除了一些众所周知的英文缩写,如IP、CPU、FDA,所有的英文缩写在文中第一次出现时都应该给出其全称。文章标题中尽量避免使用生僻的英文缩写。
在平衡生长条件下,对于缺陷D在带电荷q的形成能 能表示为[11] :
能表示为[11] :
 (1)
(1)
其中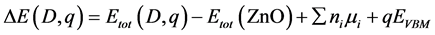 。
。 是含有缺陷D在带电荷q下的超晶胞的总能;
是含有缺陷D在带电荷q下的超晶胞的总能; 是纯净ZnO的总能;
是纯净ZnO的总能; 是i元素的个数,当i加进体系时,
是i元素的个数,当i加进体系时, 为负;当替换时,
为负;当替换时, 为正;
为正; 是i的化学势;
是i的化学势; 是费米能级,其变化范围为(0,
3.4 eV);
是费米能级,其变化范围为(0,
3.4 eV); 为纯净ZnO相对于价带顶的能
为纯净ZnO相对于价带顶的能
 (a) (b) (c) (d)
(a) (b) (c) (d)
Figure 1. The supercell structures of pure-ZnO and N-S codoped ZnO
图1. 纯净ZnO和各种掺杂体系的超晶胞
表1. 各种体系的晶格常数和离化能
量; 是i参考其元素结合的变化的化学势,小于零。为了保持稳定的ZnO复合体,避免其他复合体的生成,应该满足以下关系式:
是i参考其元素结合的变化的化学势,小于零。为了保持稳定的ZnO复合体,避免其他复合体的生成,应该满足以下关系式:
 (2)
(2)
 (3)
(3)
其中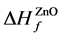 ,
, 分别是ZnO,ZnS的形成熵。
分别是ZnO,ZnS的形成熵。
离化能为当缺陷D带电荷q时的形成能和当缺陷D带电荷q'时的形成能相等时的费米能级就是离化能。因此,离化能可以这样计算[11] :
 (4)
(4)
图2为采用NO作为掺杂源不同体系不同生长条件下的形成能。在两种生长条件:(a) 在富O条件下: = 0,
= 0,
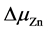 = −3.449 eV,
= −3.449 eV,
 = 0.751 eV,
= 0.751 eV,
 = −3.442 eV;(b) 在富Zn条件下:
= −3.442 eV;(b) 在富Zn条件下: = 0,
= 0,
 = −3.449 eV,
= −3.449 eV,
 = 4.2 eV,
= 4.2 eV,
 = −5.767 eV。从公式(1)得知:斜率代表电荷数。从图中知,每种复合体的离化能是交点。化学势是和两种生长条件有关。
= −5.767 eV。从公式(1)得知:斜率代表电荷数。从图中知,每种复合体的离化能是交点。化学势是和两种生长条件有关。
在富O条件下,我们发现费米能级 移向价带顶,N-S复合体的形成能最低,这表明N-S很容易掺入体系中,同时表明N-S共掺杂能够提高N的溶解度。然而,N-S复合体的离化能为0.72
eV(如表1所示),这个离化能比N单掺(0.34 eV)高。因此,我们得出结论:N-S复合体不能制备良好的p型ZnO。
移向价带顶,N-S复合体的形成能最低,这表明N-S很容易掺入体系中,同时表明N-S共掺杂能够提高N的溶解度。然而,N-S复合体的离化能为0.72
eV(如表1所示),这个离化能比N单掺(0.34 eV)高。因此,我们得出结论:N-S复合体不能制备良好的p型ZnO。
然而,在富Zn条件下,情况刚好相反。当费米能级接近价带顶时,3N-S复合体的形成能在所有复合体中最低,这表明:3N-S复合体最容易形成,而且溶解度也很好。同时,3N-S的离化能为0.3 eV比N单掺杂(0.34 eV)低,这表明3N-S掺杂能够提高N原子的活性,能够制备p型导电率的ZnO。因此,我们预测3N-S复合体很可能提高p型ZnO的导电率。
3.2. 电子结构和导电率
首先,我们计算了各种复合体的导电率。各种复合体的总态密度如图3所示。我们在orgin8.0里使

(a) 在富O条件下(b) 在富Zn条件下
Figure 2. Formation energies of N-S codoping complexes
图2. N-S掺杂ZnO的形成能

Figure 3. TDOS of varies complexes
图3. 各种复合体的总态密度
用积分计算了从费米能级到价带顶的面积,即为空穴数。通过计算得到N-S,2N-S,3N-S复合体的空穴数分别为1.0628、1.7363、3.6644。我们发现随着掺杂物浓度的提高,空穴数也增多。需要指出的是:半导体的导电性不仅由载流子数决定,还取决于其平均自由时间。根据固体物理理论,平均自由时间与杂质浓度成反比关系,即 。在这里,我们对N-S,2N-S,3N-S复合体计算的掺杂浓度分别为4.9598 ×
1021 cm−3、7.4511 × 1021 cm−3、9.9276
× 1021 cm−3。由于我们考虑的体系呈现为p型,则空穴导电率[12] 为:
。在这里,我们对N-S,2N-S,3N-S复合体计算的掺杂浓度分别为4.9598 ×
1021 cm−3、7.4511 × 1021 cm−3、9.9276
× 1021 cm−3。由于我们考虑的体系呈现为p型,则空穴导电率[12] 为:
 (5)
(5)
其中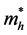 为空穴有效质量;
为空穴有效质量; 为空穴掺杂浓度;q电荷数;
为空穴掺杂浓度;q电荷数; 平均自由时间;
平均自由时间; 导体的导电率。因此各种复合体的导电率之比可以这样计算。设置N-S,2N-S,3N-S复合体的导电率分别为
导体的导电率。因此各种复合体的导电率之比可以这样计算。设置N-S,2N-S,3N-S复合体的导电率分别为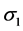 、
、 、
、 ,则有:
,则有:


很明显,从以上结果得出: <
<
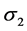 <
< 。因此,我们得出结论:3N-S共掺杂可以提高p型ZnO的导电率。
。因此,我们得出结论:3N-S共掺杂可以提高p型ZnO的导电率。
接着,为了进一步细致分析3N-S复合体,计算了3N-S复合体的分波态密度。如图4所示。价带被分成3部分:上价带从−6.37到0.49 eV主要由N-2p态、S-3p态、Zn-3d态和O-2p态决定;中间价带从−13.51到−12.76 eV这个范围内主要是由N-2s态和S-3s态贡献。然而,最低价带在−17.81到−16.92 eV范围内主要是由O-2s态决定。然而,导带部分主要是由Zn-4s态贡献。
3.3. 光学性质
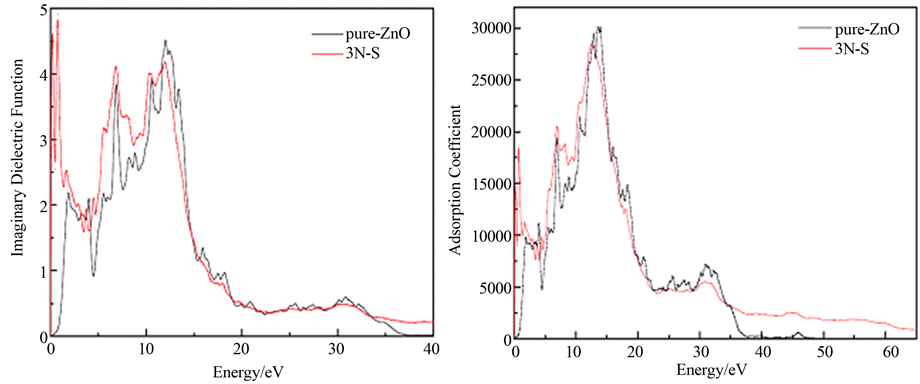
图5(a)为3N-S复合体和纯净ZnO的介电函数的虚部。在计算中主要考虑电场垂直于c轴(E‖c-axis)

Figure 4. PDOS of 3N-S complex
图4. 3N-S复合体的分波态密度
 (a) (b)
(a) (b)
Figure 5. (a) Imaginary dielectric function; (b) Adsorption coefficient
图5. (a) 介电函数的虚部;(b) 吸收系数
的情况。我们知道,介电函数的虚部与电子激发有关。从图中得到,纯净ZnO有5个介电峰分别为1.83、3.97、6.85、10.58及11.99 eV。第一个介电峰主要是Zn-4s态和O-2p态之间的跃迁。第二、三和第四个介电峰都主要来自于Zn-3d态和O-2p态的跃迁。而第五个介电峰来自于Zn-3d态和O-2s态的跃迁。这个结论和Sun Jian[13] 的结果相吻合。
然而,对于3N-S复合体,如图5所示,同样也有5个介电峰,分别为:0.21、0.79、6.82、10.37及11.99 eV。在0.21 eV处出现一个新的介电峰,主要是由Zn-4s态与N-2p态、S-2p态的电子跃迁引起的。在0.79 eV的介电峰,主要是由Zn-3d态与N-2p态的电子跃迁引起的。在6.82 eV的介电峰,主要是由Zn-3d态与O-2p态的电子跃迁引起的。第四个介电峰主要来自于Zn-3d态与O-2p态、N-2p态、S-2p态之间的跃迁。在11.99 eV的介电峰,主要是由Zn-3d态与O-2s态的电子跃迁引起的。和纯净ZnO相比,3N-S复合体的介电峰在一定程度上向低能方向移动,而在高能方向上的峰值强度基本保持不变。同时需要指出的是,在低能方向出现一个新的介电峰,而且强度很大。主要是由N和S的高掺杂缺陷浓度引起。通过跟前面计算的电子结构对比,发现:3N-S复合体在费米能级附近有很多的N-2p占据态,这导致N-2p占据态比O-2p态多。因此,新出现的峰值在低能区提高了强度。这就是3N-S共掺杂ZnO在低能区有明显特性。这主要是由于较高的杂质浓度形成的。另外,由于S杂质的引入,使得原子间的相互吸引作用增加,从而导致了Zn-4s态在导带底被拉低,同时在价带的量子态提高。这一切导致了在低能区出现奇特的特性。
为了更好理解3N-S复合体的光学性质,我们计算了纯净ZnO和3N-S复合体的吸收系数。如图5(b)所示。纯净ZnO的吸收边为0.71 eV,这与我们前面计算的能隙相一致[14] 。而3N-S共掺杂在低能区导致光吸收边的增加。同时,发现在0.74 eV处出现一个新的尖锐的吸收峰。另外,我们发现3N-S复合体的吸收峰向低能方向移动,这一结果与态密度图4相一致。
4. 结论
基于密度泛函理论的第一性原理计算,分析了N-S共掺杂ZnO的电子结构和光学性质。计算结果表明:3N-S复合体不仅能提高N受主的溶解度,而且可以得到浅受主能级。这有利于得到高质量稳定p型ZnO。同时,通过计算光学性质发现:3N-S复合体在低能区有奇特的特性。我们希望我们的理论研究在不久的将来能通过实验来证实。
参考文献 (References)
- [1] Wan, Q.X., Xiong, Z.H., Dai, J.N., Rao, J.P. and Jiang, F.Y. (2008) First-principles study of Ag-based p-type doping difficulty in ZnO. Optical Materials, 30, 817-821.
- [2] Xu, W.Z., Ye, Z.Z., Zhou, T., Zhao, B.H., Huang, J.Y., et al. (2004) Low-pressure MOCVD growth of p-type ZnO thin films by using NO as the dopant source. Journal of Crystal Growth, 265, 133.
- [3] Yamamoto, T. and Katayama-Yoshida, H. (1999) Solution using a codoping method to unipolarity for the fabrication of p-type ZnO. Journal of Applied Physics, 38, L166.
- [4] Chen, L.L., Xiong, Z.H., Wan, Q.X. and Li, D.M. (2010) Realization of p-type ZnO by (nN, Mg) codoping from first-principles. Optical Materials, 32, 1216-1222.
- [5] Xiong, Z.H., Chen, L.L., Zheng, C.D., et al. (2010) A pathway to p-type conductivity in (nN, B)-codoped ZnO. Scripta Materialia, 63, 1069-1072.
- [6] Duan, X.-Y., Zhao, Y.-J. and Yao, R.-H. (2008) Pushing p-type conductivity in ZnO by (Zr, N) codoping: A firstprinciples study. Solid State Communications, 147, 194.
- [7] Wei, F.Y., Ni, L.S. and Cui, P. (2008) Preparation and characterization of N-S codoped TiO2 photocatalyst and its photocatalytic activity. Journal of Hazardous Materials, 156, 135-140.
- [8] Wen, J., Zuo, C.Y., Xu, M., Zhong, C. and Qi, K. (2011) First-principles investigation of electronic structure and optical properties in N-F codoped ZnO with wurtzite structure. European Physical Journal B, 80, 25-30.
- [9] Kresse, G. and Hafner, J. (1994) Ab initio molecular dynamics for liquid metals. Physical Review B, 47, 558.
- [10] Kresse, G. and Furthermuller, J. (1996) Efficiency of ab-initio total energy calculations using a plane-wave basis set. Physical Review B, 54, 11169.
- [11] Yan, Y.F. and Wei, S.H. (2008) Doping asymmetry in wide-bandgap semiconductors: Origins and solutions. Physica Status Solidi (b), 245, 641-652.
- [12] Huang, K. and Han, N.Q. (1985) Solid state physics. Higher Education Press, Beijing.
- [13] Sun, J., Wang, H.T., He, J.L. and Tian, Y.J. (2005) Ab initio investigations of optical properties of the high-pressure phases of ZnO. Physical Review B, 71, 125132.
- [14] Chen, L.L., Xiong, Z.H., Wan, Q.X., et al. (2010) First-principles calculations for geometrical structures and electronic properties of nN-Mg codoped ZnO. Proceedings of SPIE, 7658, 76581M.
