Material Sciences
Vol.
12
No.
11
(
2022
), Article ID:
57802
,
6
pages
10.12677/MS.2022.1211118
基于有限元的长轴杆件硬质涂层的热应力研究
王靖文,宋慧瑾*,王自龙
成都大学机械工程学院,四川 成都
收稿日期:2022年10月17日;录用日期:2022年11月2日;发布日期:2022年11月14日

摘要
长轴杆件零部件因其结构的特殊性在表面硬质涂层的制备过程中受到一定限制。本文利用有限元模拟计算了长轴杆件表面Ti系涂层在600℃环境温度范围内杆件的热应力变化及涂层厚度对基体和涂层的影响。结果表明:在涂层制备过程中,杆件热应力在两端会出现应力集中,且随着温度上升,应力逐渐向杆件中间部分扩散,温度稳定后,应力集中现象逐渐消失;基体两端表面随着温度上升,出现中心应力低于四周应力的现象,使用的四种Ti系涂层材料中TiAlN涂层的热应力最大,为74.02 MPa,Ti的热应力最小,为38.01 MPa。涂层厚度的增加,在5~9 μm范围内,TiAlN涂层的热应力变化不明显。
关键词
有限元分析,热应力,ABAQUS软件,热力耦合

Study on Thermal Stress of Hard Coating of Long Axis Bar Based on Finite Element
Jingwen Wang, Huijin Song*, Zilong Wang
School of Mechanical Engineering, Chengdu University, Chengdu Sichuan
Received: Oct. 17th, 2022; accepted: Nov. 2nd, 2022; published: Nov. 14th, 2022

ABSTRACT
Due to the particularity of its structure, long axis bar parts in the surface hard coating preparation process are limited. In this paper, the thermal stress variation of Ti-based coating on the surface of long axis bar in 600˚C ambient temperature is calculated and the influence of coating thickness on the substrate and coating is simulated by finite element method. The results show that during the coating preparation process, the thermal stress of the rod will be concentrated at both ends, and as the temperature rises, the stress gradually diffuses to the middle part of the rod. After the temperature is stable, the stress concentration phenomenon gradually disappears. With the increase of temperature at both ends of the substrate, the central stress is lower than the surrounding stress. Among the four Ti-based coating materials used, the thermal stress of TiAlN coating is the largest, 74.02 MPa, and the thermal stress of Ti is the smallest, 38.01 MPa. With the increase of coating thickness, the thermal stress of TiAlN coating does not change obviously in the range of 5~9 μm.
Keywords:Finite Element Analysis, Thermal Stress, ABAQUS Software, Thermal Coupling

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
物理气相沉积(PVD)制备的硬质涂层因其优异的机械性能被广泛应用于保护层,改善基体表面性能和表面形貌,从而提高工件使用寿命 [1]。但涂层易受载荷影响而失效从而使涂层从基体上剥落或者涂层发生断裂。其中剥落是涂层与基体结合力较弱,在受到载荷时因脱落而失效。影响结合力的残余应力是热应力、内应力和外应力共同作用的结果 [2]。所以研究涂层制备过程中热应力大小及分布规律对硬质涂层的应用具有重要意义。
PVD技术因其环境友好性及自身优越性广泛应用于硬质涂层制备中。在涂层制备工程中 ,因PVD设备及工艺的复杂性,对其某些具体参数的实时检测及对涂层及基体的影响分析带来一定困难。运用有限元方法对涂层进行硬质涂层制备过程进行模拟分析,加载制备工艺条件,可以对所需求解的问题进行简化,对实际制备进行预测与指导,并且运用有限元可以解决或计算常规情况难以计数的量、难以观察的量等 [3]。国际上,R. Ali,M. Sebastiani等人运用有限元方法研究了Ti-TiN多层PVD涂层设计对残余应力和附着力的影响 [4];Yan等研究了无摩擦层与梯度功能材料涂层半平面之间未粘合接触的半分析和有限元解决方案 [5];Sun等进行了单一粗糙度与不同材料弹性塑性接触的有限元分析 [6]。Yilmaz等人进行了均匀正交各向异性涂层–各向同性基板系统的滑动摩擦接触问题的解析和有限元解 [7]。Vlachomitrou等完成了脉动涂层微气泡与刚性壁之间相互作用的数值研究 [8]。Bolot, R.等人进行了有限元在热机械估算中应用等离子喷涂复合涂层的特性研究 [9]。Hu,Z.C.等人通过有限元的方法进行了高温阻隔涂层的相关模拟,用以研究涂层的热力失效机理 [10]。
本文利用abaqus软件对以高速钢(HSS) (具体材料为W18Cr4V)为基体的长轴件,Ti系材料为涂层或镀膜的梯度硬质合金进行热应力分析,模拟分析在镀膜过程中基体与涂层的应力变化,为长轴杆状零部件的制备工艺提供理论指导。
2. 模型建立与仿真分析
基体材料为HSS (W18Cr4V),涂层材料为Ti系材料的单一涂层或复合梯度涂层,模拟计算中使用的涂层参数如表1所示。
由于基体与涂层均具有轴对称性,为减少计算量,将模型简化取杆件1/4部分进行模拟计算分析,热应力模型如图1所示,长杆件长径比为1: 10。Ti,TiN涂层厚度为200 nm,TiAlN,TiCNT涂层厚度为5~9 μm。热应力模拟中,为符合实践生产中器械对基体的夹持,对杆件两端进行了自由度约束。由此进行的简化设计较为合理,且能减少模拟计算量。
Table 1. Coating parameters
表1. 涂层参数

Figure 1. Thermal stress simulation block diagram
图1. 热应力模拟结构图
在利用abaqus软件进行的建立模型过程中,采用温度位移耦合分析,以得到温度变化带来的杆件应力应变位移等的变化,结合实际影响,着重观察了温度带来的应力变化。进行模型构建,属性定义,模型装配之后,选择好温度位移的分析步后,对杆件两端进行了自由度设置,网格划分进行自定义划分,基体部分网格较大,尺寸设置为在0.05 mm,基体网格数均大于20,000,薄膜或涂层则根据不同厚度进行了细划,网格单元指派类型为温度位移耦合类型 [2]。实际镀膜过程中热源由热辐射(主要),热对流,热传递共同组成,模拟过程并未对 其构成进行具体组成区分,采用直接赋予温度具体数值的方法。为减小计算量,模拟过程中将涂层与基体的材料均看作各向同性材料。
3. 结果与讨论
图2为20℃至600℃升温过程中,Ti,TiN,TiCN,TiAlN涂层的热应力云图。可以看出,温度由20℃至600℃升温过程中,基体与涂层均会出现两端应力集中,其两端的应力大于中间部分应力,温度上升过程中,此现象会一直存在,当温度逐渐保持在最高温度(模拟中最高温度为600℃)后,应力集中的现在逐渐消失,基体与涂层的应力分布均匀。此外,加热过程中基体两端表面会出现中心应力小于周边应力的现象,这种现象在600℃保温时仍存在。涂层从加热开始就出现两端应力集中的现象,温度达到600℃时,仍存在这样的现象。因此,在长轴件表面采用PVD技术制备硬质涂层工艺中,要严格控制基体升温速率,防止应力集中出现。
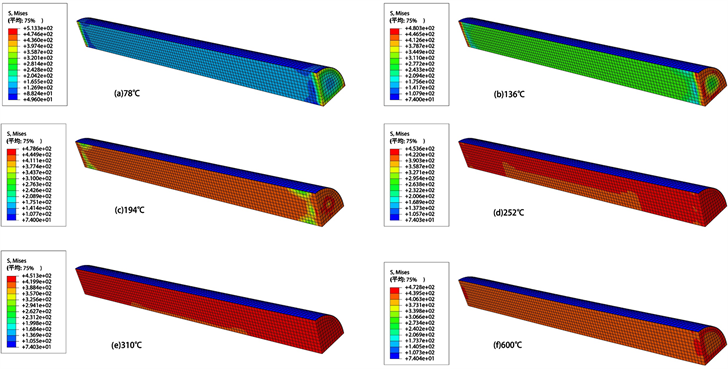
Figure 2. Stress change process
图2. 应力变化过程
图3为Ti,TiN,TiCN,TiAlN厚度分别为200 nm,200 nm,5 μm,5 μm的600℃时的热应力图。根据模拟结果可知,在最终温度600℃时,四种材料都存在数值在480 MPa左右的积分点,但基体整体热应力基本在422 MPa,薄膜Ti的热应力大小为38.01 MPa,薄膜TiN的热应力大小为43.01 MPa,TiCN涂层的应力大小为66.02 MPa。TiAlN涂层的应力大小为74.02 MPa。根据模拟结果,在薄膜Ti上进行TiCN与TiAlN涂层镀膜,涂层并未对薄膜的热应力大小产生较大影响,薄膜的热应力与未进行涂层镀膜时数值接近。

Figure 3. Ti, TiN, TiCN, TiAlN, Thermal stress plot at 600˚C
图3. Ti,TiN,TiCN,TiAlN四种材料600℃时的热应力图
图4为结构为Ti/TiN/TiCN与Ti/TiN/TiAlN梯度涂层的热应力模拟结果。可以看出Ti/TiN/TiAlN三层梯度涂层的最大积分点应力为481.3 MPa,Ti/TiN/TiCN三层涂层存在最大积分点应力为480.1 MP,两种梯度涂层的基体整体处于422 MPa,最外层涂层为TiCN时,最大热应力为66 MPa,最外层涂层为TiAlN时,最大热应力为74 MPa。通过热应力模拟结果发现,梯度涂层的最大热应力与单层涂层的最大热应力数值接近,无较大变化。

Figure 4. TICN, TiAlN, Stress of both materials at 600 degrees Celsius
图4. TICN,TiAlN,两种材料在600摄氏度下的应力
图5为对结构为Ti/TiN/TiAlN梯度涂层在TiAlN 5~9 μm下的热应力云图。通过模拟结果发现,可以看出,涂层厚度从5 μm增加至9 μm,涂层的应力在74 MPa左右浮动,基体的应力在逐渐减小,但减小幅度只在0.6 MPa左右。其中最大积分点的应力从479.6 MPa逐渐降低至479.0 MPa,基体整体的应力依旧在422 MPa附近浮动。厚度从5 μm增加至9 μm,对涂层和基体的热应力影响也较小。
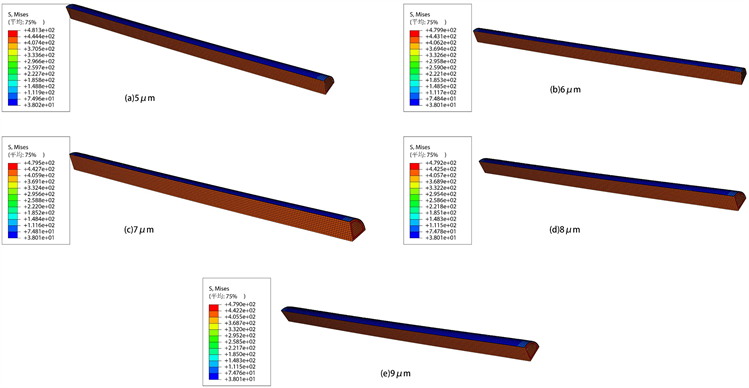
Figure 5. 5~9 μm, Stress on TiAlN coatings
图5. 5~9 μm,TiAlN涂层的应力
4. 结论
由上面研究分析得出:
1) 制备环境温度在20℃~600℃升温过程中,基体与涂层的热应力均在两端存在应力集中的情况,同一温度条件,但未加热至最终稳定状态前,热应力存在两端热应力大于中间部分热应力的情况。加热至最高温度且稳定之后,基体与涂层各位置热应力均达到最高值不再变化。加热过程中,基体两端表面出现中心应力小于四周应力的现象,并且这一现象在温度达到最高点时,仍然存在。
2) 在600℃制备环境温度下,单层打底层Ti涂层的最大热应力为38.01 MPa,单层缓冲层TiN薄膜的最大应力为43.01 MPa,单层TiCN涂层的最大应力为66.02 MPa,单层TiAlN涂层的最大应力为74.02 MPa。基体HSS的热应力受涂层应力影响较小,在环境温度600℃下,其热应力最终稳定在422 MPa,但基体中存在极少的大于422 MPa的积分点。
3) Ti/TiN/TiAlN梯度涂层的最大积分点热应力为481.3 MPa,Ti/TiN/TiCN梯度涂层的热应力为480.1 MPa。但两者在最高温度时,基体整体的热应力都在422 MPa。
4) Ti/TiN/TiAlN梯度涂层,在600℃制备环境温度下,TiAlN梯度涂层厚度在5~9 μm时,涂层与基体的热应力变化较小。
致谢
本文由四川省粉末冶金工程技术研究中心开放基金项目(SC-FMYJ2019-06)硬质涂层在石油气压缩机活塞杆表面改性中的应用及性能研究项目资助。
基金项目
四川省粉末冶金工程技术研究中心开放基金项目(SC-FMYJ2019-06)硬质涂层在石油气压缩机活塞杆表面改性中的应用及性能研究。
文章引用
王靖文,宋慧瑾,王自龙. 基于有限元的长轴杆件硬质涂层的热应力研究
Study on Thermal Stress of Hard Coating of Long Axis Bar Based on Finite Element[J]. 材料科学, 2022, 12(11): 1064-1069. https://doi.org/10.12677/MS.2022.1211118
参考文献
- 1. 宋慧瑾, 鄢强, 李玫, 董志红, 杨强. 梯度纳米硬质涂层内部应力的有限元分析[J]. 真空科学与技术学报, 2015, 35(6): 726-731. https://doi.org/10.13922/j.cnki.cjovst.2015.06.15
- 2. 邹微微, 王玉霞, 徐扬, 张秀. AlN薄膜的热应力模拟计算[J]. 光机电信息, 2011, 28(1): 10-14.
- 3. 周溯源. 氮硼化钛基纳米复合涂层制备、表征及性能研究[D]: [博士学位论文]. 武汉: 武汉大学, 2016.
- 4. Ali, R., Sebastiani, M. and Bemporad, E. (2015) Influence of Ti-TiN Multilayer PVD-Coatings Design on Residual Stresses and Adhesion. Materials & Design, 75, 47-56. https://doi.org/10.1016/j.matdes.2015.03.007
- 5. Yan, J., Mi, C.W. and Liu, Z.X. (2019) A Semianalytical and Finite-Element Solution to the Unbonded Contact between a Frictionless Layer and an FGM-Coated Half-Plane. Mathe-matics and Mechanics of Solids, 24, 448-464. https://doi.org/10.1177/1081286517744600
- 6. Sun, Z.N., Li, X.P. and Li, X.H. (2021) The Finite Element Analysis of Elastic-Plastic Contact of Single Asperity with Different Materials. 2021 7th International Conference on Condition Monitoring of Machinery in Non-Stationary Operations (CMMNO), Guangzhou, 11-13 June 2021, 108-114. https://doi.org/10.1109/CMMNO53328.2021.9467539
- 7. Yilmaz, K.B., et al. (2019) Analytical and Finite Ele-ment Solution of the Sliding Frictional Contact Problem for a Homogeneous Orthotropic Coating-isotropic substrate sys-tem. Journal of Applied Mathematics and Mechanics, 99, e201800117. https://doi.org/10.1002/zamm.201800117
- 8. Maria, V. and Pelekasis, N. (2021) Numerical Study of the Interac-tion between a Pulsating Coated Microbubble and a Rigid Wall. I. Translational Motion. Physical Review Fluids, 6, Arti-cle ID: 013601. https://doi.org/10.1103/PhysRevFluids.6.013601
- 9. Bolot, R., Aussavy, D. and Montavon, G. (2017) Applica-tion of FEM to Estimate Thermo-Mechanical Properties of Plasma Sprayed Composite Coatings. Coatings, 7, 12 p. https://doi.org/10.3390/coatings7070091
- 10. Hu, Z.C., Liu, B., Wang, L., et al. (2020) Research Progress of Failure Mechanism of Thermal Barrier Coatings at High Temperature via Finite Element Method. Coatings, 10, 25 p. https://doi.org/10.3390/coatings10080732
NOTES
*通讯作者。
