Computer Science and Application
Vol.
10
No.
03
(
2020
), Article ID:
34405
,
10
pages
10.12677/CSA.2020.103041
Research on the Machine Vision Applicability of Linear Filtering Algorithm
Chenbo Jiang, Jingde Huang
Zhuhai College of Jilin University, Zhuhai Guangdong

Received: Feb. 15th, 2020; accepted: Feb. 30th, 2020; published: Mar. 4th, 2020

ABSTRACT
In the actual working process of machine vision system, due to the diversity of state noise, it is difficult to choose the best filtering algorithm in real time. In this paper, the linear filtering algorithm: Instant Domain Recursive filtering (IDR), Gaussian filtering, Laplace of Gaussian filtering (LOG), Binomial Coefficient filtering (BC) algorithm model, calculation speed and output results are studied in depth. The performance of the above algorithm is tested by superposition random noise combination, and its applicability in engineering practice is analyzed. The experimental results show that Gaussian filtering achieves the best compromise between time and accuracy when white noise and Gaussian noise are superimposed; when salt and pepper noise are superimposed, Gaussian Laplace filtering is obviously superior to the other three algorithms, providing theoretical and technical support for the optimization of image processing effect of machine vision system.
Keywords:Machine Vision, Linear Filtering, Noise Superposition, Applicability Analysis

线性滤波算法的机器视觉适用性研究
姜晨波,黄景德
吉林大学珠海学院,广东 珠海

收稿日期:2020年2月15日;录用日期:2020年2月30日;发布日期:2020年3月4日

摘 要
在机器视觉系统实际工作过程中,由于状态噪声的多样性,很难实时选择出最佳滤波算法。论文针对线性滤波算法:时域递归滤波、高斯滤波、高斯–拉普拉斯滤波、二项式系数滤波的算法模型、计算速度、输出结果进行了深入研究,通过迭加随机噪声组合测试了上述算法的性能,分析了其在工程实际中的适用性。实验结果表明,在迭加白噪声与高斯噪声时,高斯滤波实现了时间与精度的最佳折中;在迭加椒盐噪声时,高斯–拉普拉斯滤波明显优于其它三种算法,为机器视觉系统优化图像处理效果提供了理论和技术支持。
关键词 :机器视觉,线性滤波算法,噪声迭加,适用性分析

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
滤波是模式识别、图像增强和复原等领域的关键技术,其在机器视觉分析与处理过程中起着至关重要的作用。如一张原始图像在获取与传递的过程中难免受到各种噪声的干扰,使得图像的质量下降,图像的分析难度大幅度提高 [1]。如何在保留图像有效信息的同时滤除噪声,以及在不同图像环境下各种滤波算法的选择一直是数字图像处理领域的重大难题。在滤波技术中,根据输入函数是否为线性函数可以分为线性滤波和非线性滤波两种。线性滤波为原始数据采用算术运算实现,有固定的模板。并以其易于数学处理、易于采用快速傅里叶变换(fast Fourier transform)和具有完善的理论基础等优势,长期在图像的滤波处理领域中占有重要的地位。工程实际中,非线性滤波是一种对输入信号序列的映射关系,在非线性滤波时,常将某一特定的噪声近似映射为零,从而达到保留图像重要特征的效果 [2]。
当前,国内外学者围绕滤波算法的改进取得了丰富的研究成果 [3] [4] [5]。但是,由于算法本身的弊病和状态噪声的多样性,在机器视觉实际应用中,为了达到较为理想的效果,需根据图像环境选择不同的滤波算法 [6] [7] [8] [9] [10]。因此,研究各型线性滤波算法的适用性具有重大的意义。本文重点分析了典型线性滤波算法在机器视觉系统中的应用,根据对输入图像迭加随机噪声组合,对比不同平滑量下的计算时间及输出结果,分析其在实际工作中的适用性,为提高机器视觉系统的开发与工作效率提供技术支持。
2. 使用须知
2.1. 时域递归滤波
时域递归滤波由CBS实验室于1971年提出,其在降低图像的随机噪声、提高图像信噪比和图像质量方面具有良好的效果。对于数字摄像系统而言,大部分噪声是随机的,如果以1帧为周期,对图像信息在时域做加权平均,则可在保留图像信号的同时大大降低噪声。当采集到两帧图像进入缓存区后,将当前帧与前一帧的差乘滤波系数k作为当前帧的滤波图像,并存入缓存区作为输入的前一帧,再将第三帧作为输入的当前帧进行循环运算。即
(1)
式(1)如果存在一帧延时 ,则其传递函数可以表示为
(2)
其幅频特性可以表示为
(3)
由(3)式可知,滤波系数k应位于0~1之间
(4)
式(4)如果成立,递归滤波对信噪比的改善程度可以表示为
(5)
由式(5)可得,当 之后,P的变化趋势加快,对降噪较为有利。
2.2. 高斯滤波
高斯滤波主要用于得到SNR较高的图像,反应真实信号。当用
表示中心像素
大小为
(M为奇数)的邻域,用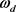 表示空间距离相似权重时,其可以表示为
表示空间距离相似权重时,其可以表示为
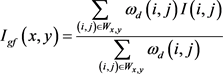 (6)
(6)
高斯滤波的局部相似性取决于像素点p水平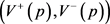 和垂直
和垂直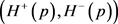 方向上的跨度,高斯掩模的区域同样由该方向集上的臂长
方向上的跨度,高斯掩模的区域同样由该方向集上的臂长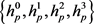 决定,而相似度参考值由臂长方向的像素权值实时分配 [4]。以点p的
决定,而相似度参考值由臂长方向的像素权值实时分配 [4]。以点p的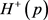 方向为例,其相似度参考函数为
方向为例,其相似度参考函数为
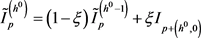 (7)
(7)
式(7)中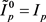 ,
,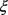 为权值分配参数。
为权值分配参数。
由于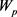 限制了固定掩模的大小,则
限制了固定掩模的大小,则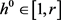 。因此,
。因此,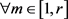 ,臂长特征
,臂长特征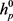 需满足
需满足
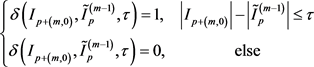 (8)
(8)
式(8)中, 为灰度相似度阈值。由此,
为灰度相似度阈值。由此,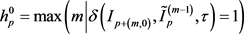 ,同理,对于
,同理,对于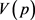 上任意点p,均可根据式(7)与式(8)求得其在垂直方向上的跨度
上任意点p,均可根据式(7)与式(8)求得其在垂直方向上的跨度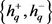 ,所以,高斯掩模的区域
,所以,高斯掩模的区域 可以用式(9)表示
可以用式(9)表示
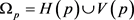 (9)
(9)
2.3. 高斯–拉普拉斯滤波
LOG算法来源于Marr提出的边缘检测思想其对图像的平滑采用二维高斯函数
 (10)
(10)
其中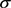 是空间分布系数。对式(10)取拉氏变换可得
是空间分布系数。对式(10)取拉氏变换可得
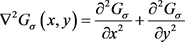 (11)
(11)
求解式(11)可得二维LOG算子的函数形式
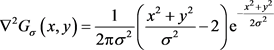 (12)
(12)
将式(12)与原图像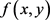 进行卷积
进行卷积
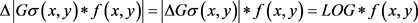 (13)
(13)
对式(10)求偏导,然后进行卷积可解得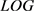 ,公式具体表示为
,公式具体表示为
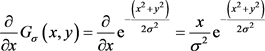 (14)
(14)
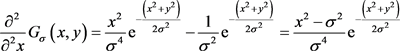 (15)
(15)
因此,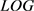 核函数为
核函数为
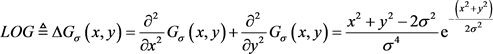 (16)
(16)
将式(16)代入式(12)可解得输出图像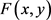
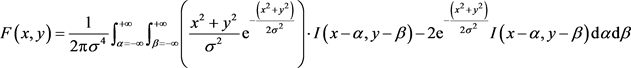 (17)
(17)
2.4. 二项式系数滤波
在实验中观察到的信号通常为噪声和目标信号的迭加形式,即
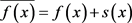 (18)
(18)
式(18)中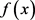 为目标信号,
为目标信号,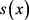 为噪声。为了尽可能的滤除噪声,使
为噪声。为了尽可能的滤除噪声,使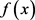 从
从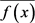 分离出来,可以定义某种运算A,使得
分离出来,可以定义某种运算A,使得
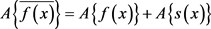 (19)
(19)
为了使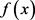 尽可能地被
尽可能地被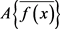 所反映,必须要求
所反映,必须要求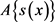 与
与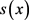 的比值被尽量压缩,为了研究运算A,假设:(1)
的比值被尽量压缩,为了研究运算A,假设:(1)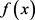 满足狄利克雷条件;(2)
满足狄利克雷条件;(2)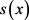 的各态历经性成立,且满足平稳假设。在条件(1)成立时,
的各态历经性成立,且满足平稳假设。在条件(1)成立时,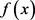 可以被看作不同三角函数的迭加;在条件(2)成立时,运算A对
可以被看作不同三角函数的迭加;在条件(2)成立时,运算A对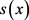 的压缩作用可以被运算前后的方差所反映。
的压缩作用可以被运算前后的方差所反映。
在实际工作时,抽样按等间距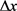 进行,得到的是
进行,得到的是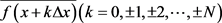 。此时,运算A的具体表现形式为
。此时,运算A的具体表现形式为
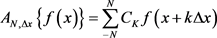 (20)
(20)
而二项式系数滤波实质上就是将二项式系数作为权系数进行滑动平均 [7],即
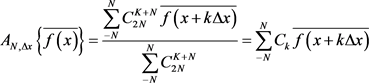 (21)
(21)
其中,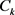 为
为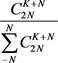 ,且式(21)有如下迭代式
,且式(21)有如下迭代式
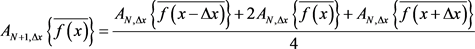 (22)
(22)
其中:当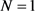 ,
,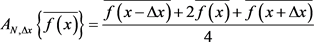
当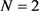 ,
,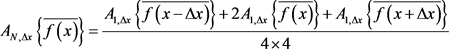
3. 实验验证
3.1. 实验对象
实验项目以HALCON数据库典型对象为基础,实验图像的规格为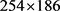 像素。通过对比上述算法在同一输入上的计算时间,以及不同平滑量下的输出结果,研究上述算法在实际工作中的适用性。算子对照见表1。
像素。通过对比上述算法在同一输入上的计算时间,以及不同平滑量下的输出结果,研究上述算法在实际工作中的适用性。算子对照见表1。
Table 1. Experimental algorithm comparison
表1. 实验算法对照
在对比不同算法的计算速度时共设置4组平滑量,以降低实验偶然因素的影响,并绘制灰度值剖面图,以更好地观察图像灰度分布的变化趋势。平滑量数据见表2。
Table 2. Experimental smoothing data
表2. 实验平滑量数据
3.2. 实验过程
将上述滤波算法将分别应用于输入图像的每个通道,并返回具有相同通道数的平滑图像。原始图像及为可视化过滤算法效果而选择的部分变体见图1。为保证实验的随机性,我们将变体应用于三种不同的随机噪声,随机噪声组合见图2。

Figure 1. Original image and input variant
图1. 原始图像及输入变体

Figure 2. Random noise combination
图2. 随机噪声组合
对输入信号使用平滑量分别为0.347、0.437、0.571、0.823的时域递归滤波,迭加白噪声、高斯噪声、椒盐噪声的输出结果分别为图3、图4、图5。

Figure 3. Results in IDR with superimposed white noise
图3. 迭加白噪声的时域递归滤波结果

Figure 4. Results in IDR with superimposed Gauss noise
图4. 迭加高斯噪声的时域递归滤波结果

Figure 5. Results in IDR with superimposed salt and pepper noise
图5. 迭加椒盐噪声的时域递归滤波结果
对输入信号使用平滑量分别为5 × 5、7 × 7、9 × 9、11 × 11的高斯滤波,迭加白噪声、高斯噪声、椒盐噪声的输出结果分别为图6、图7、图8。
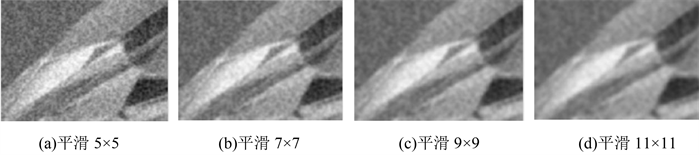
Figure 6. Results in Gauss filter with superimposed white noise
图6. 迭加白噪声的高斯滤波结果

Figure 7. Results in Gauss filter with superimposed Gauss noise
图7. 迭加高斯噪声的高斯滤波结果

Figure 8. Results in Gauss filter with superimposed salt and pepper noise
图8. 迭加椒盐噪声的高斯滤波结果
对输入信号使用平滑量分别为1.075、1.550、2.025、2.550的LOG滤波,迭加白噪声、高斯噪声、椒盐噪声的输出结果分别为图9、图10、图11。
对输入信号使用平滑量分别为5 × 5、11 × 11、17 × 17、27 × 27的二项式系数滤波,迭加白噪声、高斯噪声、椒盐噪声的输出结果分别为图12、图13、图14。

Figure 9. Results in LOG with superimposed white noise
图9. 迭加白噪声的LOG滤波结果

Figure 10. Results in LOG with superimposed Gauss noise
图10. 迭加高斯噪声的LOG滤波结果

Figure 11. Results in LOG with superimposed salt and pepper noise
图11. 迭加椒盐噪声的LOG滤波结果
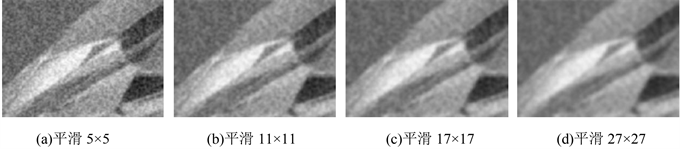
Figure 12. Results in BC with superimposed white noise
图12. 迭加白噪声的二项式系数滤波结果

Figure 13. Results in BC with superimposed gauss noise
图13. 迭加高斯噪声的二项式系数滤波结果

Figure 14. Results in BC with superimposed salt and pepper noise
图14. 迭加椒盐噪声的二项式系数滤波结果
3.3. 结果分析
由于上述滤波算法在处理不同噪声时,若平滑量一致,同一算法的计算速度并无较大差别。所以,采用算法计算的平均时间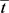 来反映在该平滑量下的算法计算速度,即
来反映在该平滑量下的算法计算速度,即
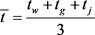 (23)
(23)
式(23)中, 为在该平滑量下处理白噪声的计算时间,
为在该平滑量下处理白噪声的计算时间,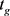 为在该平滑量下处理高斯噪声的计算时间,
为在该平滑量下处理高斯噪声的计算时间,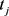 为在该平滑量下处理椒盐噪声的计算时间。
为在该平滑量下处理椒盐噪声的计算时间。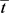 具体数据见表3。
具体数据见表3。
Table 3. Calculation time of experimental algorithm
表3. 实验算法计算时间
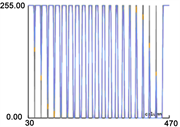
由于输出图像的灰度值分布可以帮助检查滤波算法的工作效果,灰度分布的紧凑程度可以近似为图像所含噪声的比例。因此,以4组实验的输出结果为基础绘制灰度值剖面图,以便更好地比较输出结果的灰度分布信息,以及观察其变化趋势。4组实验的灰度信息见图15。
 (a) 第一组
(a) 第一组
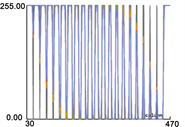 (b) 第二组
(b) 第二组
 (c) 第三组
(c) 第三组
 (d) 第四组
(d) 第四组
Figure 15. Gray section of experimental output
图15. 实验输出结果的灰度剖面图
通过以上实验结果可以看出,由于采用了线性滤波模型,除LOG滤波外,各实验算法在处理椒盐噪声时都产生了较为明显的滤波发散。在处理白噪声与高斯噪声时,时域递归滤波在滤波系数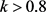 后工作效果较为明显,但其计算时间较长;高斯滤波在平滑量
后工作效果较为明显,但其计算时间较长;高斯滤波在平滑量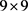 以上就能达到较为理想的效果,计算时间也较为适宜;LOG滤波的工作效果最佳,但计算时间是Gauss滤波的3倍以上;而二项式系数滤波表现最差。
以上就能达到较为理想的效果,计算时间也较为适宜;LOG滤波的工作效果最佳,但计算时间是Gauss滤波的3倍以上;而二项式系数滤波表现最差。
4. 结束语
论文在对典型线性滤波进行分析实验的基础上,通过迭加随机噪声组合测试了线性滤波算法的性能,就计算速度来说,二项式系数滤波要明显优于其它算法;从滤波效果来说,LOG滤波对椒盐噪声的处理效果最优,而Gauss滤波实现了时间与精度的最佳折中。因此,在机器视觉系统开发过程中实际选择算法时,若椒盐噪声所占比例较高,宜采用LOG滤波,在其它一般情况下,采用Gauss滤波效果更佳。并且,随着计算机处理能力的提高,Gauss滤波将具有更加广泛的应用前景。为机器视觉系统开发提供了理论和技术基础。
基金项目
本文获得吉林大学珠海学院创新能力培育工程项目(2019XJCQ002)支持。
文章引用
姜晨波,黄景德. 线性滤波算法的机器视觉适用性研究
Research on the Machine Vision Applicability of Linear Filtering Algorithm[J]. 计算机科学与应用, 2020, 10(03): 398-407. https://doi.org/10.12677/CSA.2020.103041
参考文献
- 1. 王耀贵. 图像高斯平滑滤波分析[J]. 计算机与信息技术, 2008(8): 79-81+90.
- 2. 景晓军, 李剑峰, 熊玉庆. 静止图像的一种自适应平滑滤波算法[J]. 通信学报, 2002, 23(10): 6-14
- 3. 冯鹏, 魏彪, 米德伶, 潘英俊, 于渝. 基于时域递归滤波的动态数字图像降噪[J]. 重庆大学学报(自然科学版), 2005, 28(2): 23-25+31.
- 4. 姒绍辉, 胡伏原, 顾亚军, 鲜学丰. 一种基于不规则区域的高斯滤波去噪算法[J]. 计算机科学, 2014, 41(11): 313-316.
- 5. Marr, D. and Hildreth, E. (1980) Theory of Edge Detection. Proceedings of the Royal Society of London (Series B), Biological Sciences, 207, 187-217. https://doi.org/10.1098/rspb.1980.0020
- 6. 严国萍, 何俊峰. 高斯-拉普拉斯边缘检测算子的扩展研究[J]. 华中科技大学学报(自然科学版), 2006, 34(10): 21-23.
- 7. 彭军还. 数字滤波器的两个理论公式及其应用[J]. 桂林冶金地质学院学报, 1993(4): 405-412.
- 8. 肖秀春, 彭群生, 卢晓敏, 王章野, 张雨浓, 姜孝华. 基于次序统计量像素灰度相似度的图像双边滤波[J]. 计算机辅助设计与图形学学报, 2011, 23(7): 1232-1237.
- 9. 王静, 潘梦清. 二项式系数滤波的谱特征[J]. 桂林工学院学报, 2000, 20(4): 379-382.
- 10. 刘德春, 谭信. 非线性滤波算法性能对比[J]. 电子设计工程, 2011, 19(13): 49-51.
