Operations Research and Fuzziology
Vol.07 No.03(2017), Article ID:21849,9
pages
10.12677/ORF.2017.73010
Study on Multi-Trips Whole-Transport Vehicle Scheduling Problem Based on the Multistage Network Flow Model
Zhihua Song1, Han Zhang2
1Equipment Management and Safety Engineering College, Air Force Engineering University, Xi’an Shaanxi
2Science College, Air Force Engineering University, Xi’an Shaanxi

Received: Aug. 7th, 2017; accepted: Aug. 19th, 2017; published: Aug. 28th, 2017

ABSTRACT
Multi-trips whole-transport vehicle scheduling problem is one kind of Vehicle Scheduling Problem (VSP), and the ordinary VSP algorithms haven’t made use of its special structure and behave poorly. Firstly, its structure is analyzed and the problem is transformed into a multistage network flow model. Secondly, the Bellman equation with tabu list is designed to deal with the non-monotonicity of the model, and then the dynamic programming algorithm for finding the minimum cost flow is designed. Finally, the effectiveness of the model and algorithm is verified through an example.
Keywords:Multi-Trips Whole-Transport, Vehicle Scheduling Problem, Multi-Stage Network Flow, Dynamic Programming, Tabu List
基于多阶段网络流模型的多回合整车装卸车辆调度问题研究
宋志华1,张晗2
1空军工程大学装备管理与安全工程学院,陕西 西安
2空军工程大学理学院,陕西 西安
收稿日期:2017年8月7日;录用日期:2017年8月19日;发布日期:2017年8月28日

摘 要
多回合整车装卸约束下的车辆调度问题是一种特殊的车辆调度问题,普通的车辆调度问题算法没有利用问题的特殊结构,计算效率低。首先通过分析多回合整车装卸车辆调度问题的特点,将其转换为多阶段网络流问题并建立模型;然后针对模型有后效性的特点,提出了基于禁忌列表的Bellman方程,并以此为基础,设计了基于动态规划算法的最小费用流求解算法。通过实例计算表明,模型和算法适合描述及求解多回合整车装卸车辆调度问题,能够较为快速高效地求解问题的优化行动方案。
关键词 :多回合整车装卸,车辆调度问题,多阶段网络流,动态规划,禁忌列表

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 多阶段网络流模型的建立
车辆调度问题是一类经典的NP难问题,对应的现实应用众多,分类也十分繁多 [1] ,在算法方面,以启发式算法为主流,确定性算法比较少 [2] [3] 。Rivera [4] 等人研究了多回合车辆路径问题的数学模型和精确算法,Novoa [5] 等人研究了车辆路径问题的近似动态规划方法求解,但是都是针对单车的。本文考虑一种多回合多车的整车装卸约束下的车辆调度问题。具体定义如下:
在图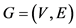 中,
中, 是点的集合,
是点的集合,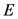 是边的集合。点集
是边的集合。点集 的子集包括停车场集合
的子集包括停车场集合 ,仓库点的集合
,仓库点的集合 ,物资需求点集合
,物资需求点集合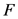 ,普通道路节点的集合
,普通道路节点的集合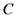 ,且有
,且有 。平时车辆停放于停车场。车辆运送物资的特点是每次从仓库点仅能装载一个单位的物资。车辆从仓库装载货物后沿规划路径到达物资需求点卸货后,要再重复执行运送任务,因此,称之为多回合整车装卸的车辆调度问题。
。平时车辆停放于停车场。车辆运送物资的特点是每次从仓库点仅能装载一个单位的物资。车辆从仓库装载货物后沿规划路径到达物资需求点卸货后,要再重复执行运送任务,因此,称之为多回合整车装卸的车辆调度问题。
由于问题是多回合的,在每个回合中,车辆都要到一个仓库装载物资然后运送到一个物资需求点,每个回合具有一定的相似性。因此,可以建立多阶段决策模型进行分析。
1) 状态定义
假设所有车辆需要完成物资运送的回合数为 ,则令多阶段决策模型的阶段数为
,则令多阶段决策模型的阶段数为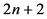 。令
。令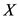 代表模型的状态集合,
代表模型的状态集合, 代表第 阶段的状态,
代表第 阶段的状态,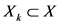 代表第
代表第 阶段状态的集合。则每个阶段的状态定义如下表1所示。
阶段状态的集合。则每个阶段的状态定义如下表1所示。
2) 状态转移
令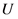 代表模型的决策变量集合。
代表模型的决策变量集合。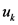 代表第
代表第 阶段可以采用的某个决策变量。记
阶段可以采用的某个决策变量。记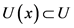 为状态
为状态 可取的决策变量集合。记
可取的决策变量集合。记 为在状态
为在状态 采用决策
采用决策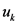 的时候所需要支付的费用,对应在
的时候所需要支付的费用,对应在 上两个点之间的距离。
上两个点之间的距离。
记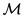 函数
函数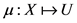 的集合,对
的集合,对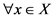 ,均有
,均有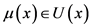 。
。
从状态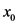 开始,采用策略
开始,采用策略 的费用为
的费用为
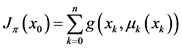
Table 1. State definition of multi-stages decision model
表1. 多阶段决策模型的状态定义
其中,状态序列 是由以下系统的状态转移方程产生
是由以下系统的状态转移方程产生
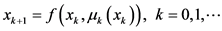
对应某辆车的优化调度目标就是寻找最优策略 ,使得总的费用最少,也即其目标函数为
,使得总的费用最少,也即其目标函数为

而问题本身要为多辆车规划路径,可以将车辆看作是模型中的网络流,而最终方案是网络上的可行流。
3) 网络流模型
令两个状态之间的弧上的单位流量费用为 ,则对应网络上停车场、仓库、物资需求点之间状态转移的费用均取其最短路的距离,虚拟状态与其他状态之间的状态转移费用根据其功能需求进行设置,具体取值如表1。弧的容量为
,则对应网络上停车场、仓库、物资需求点之间状态转移的费用均取其最短路的距离,虚拟状态与其他状态之间的状态转移费用根据其功能需求进行设置,具体取值如表1。弧的容量为 ,则对应网络上的从停车场出入的弧容量等于停车场处车辆的数量,其他弧的容量为1,参见表2。
,则对应网络上的从停车场出入的弧容量等于停车场处车辆的数量,其他弧的容量为1,参见表2。
这样,某辆车的最优调度方案对应网络流模型上的一个流量为1的可行流,此可行流必然是一个最小费用流,而反之,网络流模型的某流量为1的最小费用流却不一定对应的某个车辆的最优调度方案,此流量为1最小费用流还要满足经过的物资需求点不重复的约束,因此,通过求解网络流模型的最小费用流来得到车辆调度方案,必须要考虑一定的约束。这与网络流模型本身的结构有关。
2. 求解算法分析
令 为实值函数
为实值函数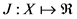 的集合,记映射
的集合,记映射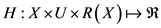 。对于任一策略
。对于任一策略 定义映射
定义映射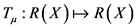 为
为
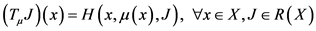
定义映射 为
为

Table 2. Unit flow cost and capacity of the edges in the network
表2. 网络上弧的单位流量费用以及容量
其中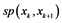 代表
代表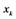 与
与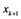 在实际网络
在实际网络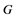 中最短路的长度。
中最短路的长度。
对于某函数 ,以及非静态策略
,以及非静态策略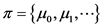 ,对于任一整数
,对于任一整数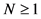 ,定义函数
,定义函数

其中,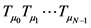 是复合函数,也就是
是复合函数,也就是

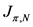 可被当作“N阶段费用函数”的表达式。
可被当作“N阶段费用函数”的表达式。
当然了,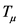 和
和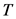 必须要满足单调性 [6] ,Bellman方程才能够成立,否则,无法应用Bellman方程递推求解。
必须要满足单调性 [6] ,Bellman方程才能够成立,否则,无法应用Bellman方程递推求解。
定义 [6] :如果满足以下条件,则认为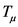 和
和 具有单调性,或者说系统具有单调性:
具有单调性,或者说系统具有单调性:
如果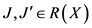 ,且
,且 ,
,
那么
证明:多阶段决策网络流模型不满足单调性。
令 ,
, ,且有
,且有

根据约束条件,不考虑重复使用发射点(可以经过),那么不妨设

并且有
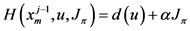
现有
那么,

因此模型不满足单调性条件,Bellman方程不能直接应用。
3. 算法设计
3.1. 基于禁忌列表的Bellman方程
按照逆向求解的思路从后至前依次分析。
1) 在第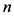 阶段的物资运送任务中,从车辆当前的状态
阶段的物资运送任务中,从车辆当前的状态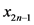 开始,根据物资需求点不重复的约束,采用策略
开始,根据物资需求点不重复的约束,采用策略 只有在满足以下条件的时候才可行,
只有在满足以下条件的时候才可行,

也就是说 和
和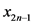 两个状态不能对应同一个物资需求点。令禁忌列表
两个状态不能对应同一个物资需求点。令禁忌列表 ,也就是其他任意阶段中,与状态
,也就是其他任意阶段中,与状态 对应同一物资需求点的
对应同一物资需求点的
状态的集合。
可行的最优方案为
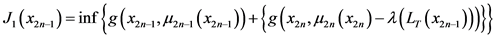
其中, ,
, 是所有的执行后会使系统转移到
是所有的执行后会使系统转移到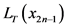 中状态的控制
中状态的控制
决策变量集合。
记
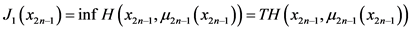

其中,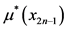 是最优策略,
是最优策略,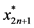 是最优策略上第
是最优策略上第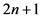 阶段的状态。
阶段的状态。
将最优策略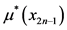 上第
上第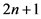 阶段的状态
阶段的状态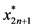 对应同一个物资需求点的所有状态加入到禁忌列表,令禁忌列表
对应同一个物资需求点的所有状态加入到禁忌列表,令禁忌列表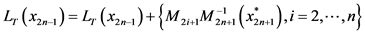 。
。
2) 在第 阶段的物资运送任务中,从车辆当前的状态
阶段的物资运送任务中,从车辆当前的状态 开始,根据物资需求点不重复的约束,采用策略
开始,根据物资需求点不重复的约束,采用策略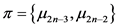 只有在满足以下条件的时候才可行,
只有在满足以下条件的时候才可行,
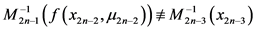
也就是说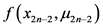 和
和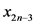 两个状态不能对应同一个物资需求点。令禁忌列表
两个状态不能对应同一个物资需求点。令禁忌列表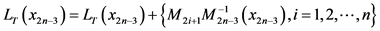 ,也就是其他任意阶段中,与状态
,也就是其他任意阶段中,与状态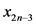 对应同一物
对应同一物
资需求点的状态的集合。
可行最优方案为

其中,

其中, 是所有的执行后会使系统转移到
是所有的执行后会使系统转移到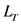 中状态的控制决策变量集合。
中状态的控制决策变量集合。
将最优策略 上第
上第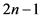 阶段的状态
阶段的状态 对应同一个物资需求点的所有状态加入到禁忌列表,令禁忌列表
对应同一个物资需求点的所有状态加入到禁忌列表,令禁忌列表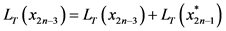 。
。
…
(k)在第 阶段的物资运送任务中
阶段的物资运送任务中 从车辆当前的状态
从车辆当前的状态 开始,根据物资需求点不重复的约束,采用策略
开始,根据物资需求点不重复的约束,采用策略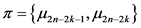 只有在满足以下条件的时候才可行,
只有在满足以下条件的时候才可行,

也就是说 和
和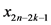 两个状态不能对应同一个物资需求点。令禁忌列表
两个状态不能对应同一个物资需求点。令禁忌列表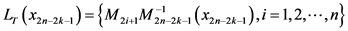 ,也就是其他任意阶段中,与状态
,也就是其他任意阶段中,与状态 对应同一物资
对应同一物资
需求点的状态的集合。
可行的最优方案为
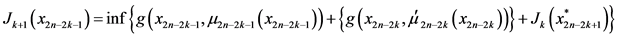
其中,

其中,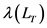 是所有的执行后会使系统转移到
是所有的执行后会使系统转移到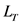 中状态的控制决策变量集合。
中状态的控制决策变量集合。
将最优策略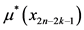 上第
上第 阶段的状态
阶段的状态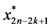 对应的禁忌列表加入本级禁忌列表,令禁忌列表
对应的禁忌列表加入本级禁忌列表,令禁忌列表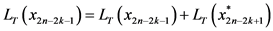 。
。
…
加入禁忌列表后,单调性满足了。
3.2. 基于禁忌列表的动态规划算法
设计多回合整车装卸车辆调度问题的算法如下:
步骤1:依照基于禁忌列表的Bellman方程寻找一条可行的最优路径方案
 作为最小费用增广链将
作为最小费用增广链将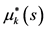 记录下来,扩充
记录下来,扩充 的流量,并令
的流量,并令 增加1。
增加1。
步骤2:在多阶段网络流模型中去掉当前已经找到的最优路径方案所包含的需求点。
步骤3:重复步骤2和步骤3,直到没有办法找到最优路径方案。
算法计算过程中找到的所有最小费用增广链,构成车辆行动方案的一个集合。通过将最小费用增广链 上点之间的弧映射回实际网络中的最短路点序列,就可以得到一个车辆行动方案。下面通过一个算例来验证算法的性能和效能。
上点之间的弧映射回实际网络中的最短路点序列,就可以得到一个车辆行动方案。下面通过一个算例来验证算法的性能和效能。
4. 计算实例及算法性能分析
某导弹部队的导弹火力单元平时隐蔽待机于待机地p1和p2,两个待机地的火力单元数量分别是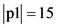 和
和 ,现接收到3波次火力打击任务,每波次都有10个火力单元发射导弹。火力单元需要通过网络机动到某一个发射点
,现接收到3波次火力打击任务,每波次都有10个火力单元发射导弹。火力单元需要通过网络机动到某一个发射点 发射导弹,然后火力单元到导弹仓库
发射导弹,然后火力单元到导弹仓库 装载导弹后,再到下一个发射点
装载导弹后,再到下一个发射点 发射导弹,假设为了隐蔽起见,在整个火力打击任务中,所有的火力单元均不会第二次使用同一个发射点,直到所有的火力单元都完成多波次火力发射任务为止。各个地点的平面坐标数据如表3所示。
发射导弹,假设为了隐蔽起见,在整个火力打击任务中,所有的火力单元均不会第二次使用同一个发射点,直到所有的火力单元都完成多波次火力发射任务为止。各个地点的平面坐标数据如表3所示。
各点的位置及相互之间的道路连接情况如图1所示,两点之间道路的长度可以使用两点之间直线的距离进行估算。
在本问题中,导弹发射车是多回合整车装卸车辆调度问题中的车辆,发射点相当于物资需求点,导弹仓库相当于物资仓库,规划导弹发射车的多波次打击行动方案,相当于规划多回合整车装卸车辆调度问题中的车辆路径,可以采用本文提出的方法求解。
算法首先根据点的平面坐标计算的各个点之间的直线距离,然后计算任意两点之间的最短路的距离,可以建立此问题的多阶段网络流模型如图2所示。
在这样的一个网络流模型中,最小费用最大流对应多车多波次导弹火力打击任务的最优行动方案。这样,多车多波次导弹火力打击行动规划问题的最优行动方案,转化为在网络流模型中寻找最小费用最大流,按照所提算法求解,可以得到网络流模型的最小费用最大流,求解过程中所找到的所有最小费用增广链如表4所示。

Figure 1. Position of vertices and the structure of the network
图1. 网络中各点的位置及网络结构
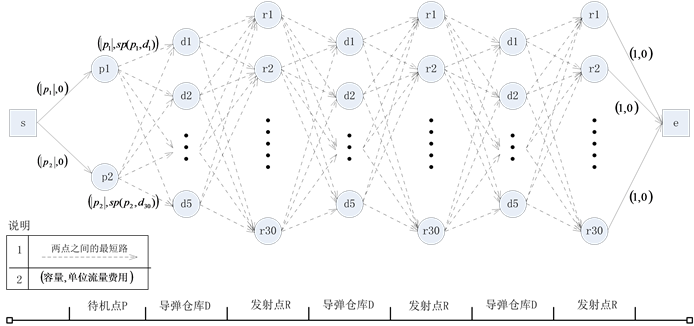
Figure 2. Multi-stages network flow model
图2. 多阶段网络流模型
Table 3. Coordinates of vertices in the network
表3. 网络中各点的平面坐标数据
Table 4. Minimum cost augmenting chains found by the algorithm
表4. 算法求解过程中所找到的最小费增广链
在上述路径中,相邻两点插入原图中的最短路方案,就可以得到发射车的火力打击行动方案。在这样的一个结果中,待机点p2仅派出了一辆发射车,而发射点p1派出了9辆发射车,究其原因,是因为p2点距离所有的仓库都比较远,大大降低了使用效率。因此,这样的计算结果,对于评估待机点或者仓库的选址位置的优劣,也是具有参考意义的。在计算机使用Matlab上实现以上算法,计算的时间为0.04秒。
5. 结束语
本文研究了多回合整车装卸条件下的车辆调度问题。根据问题多阶段的特点,建立了多阶段决策网络流模型。为了克服动态规划方法求解的非单调性,提出了基于禁忌列表的Bellman方程,用于满足物资需求点不重复的约束,然后设计了基于禁忌列表的动态规划算法求解模型的最小费用流,属于精确算法,在收敛速度和优化效果方面都具有优势。
文章引用
宋志华,张 晗. 基于多阶段网络流模型的多回合整车装卸车辆调度问题研究
Study on Multi-Trips Whole-Transport Vehicle Scheduling Problem Based on the Multistage Network Flow Model[J]. 运筹与模糊学, 2017, 07(03): 81-89. http://dx.doi.org/10.12677/ORF.2017.73010
参考文献 (References)
- 1. Kumar, S.N. and Panneerselvam, R. (2012) A Survey on the Vehicle Routing Problem and Its Variants. Intelligent Information Management, 4, 66-74.
- 2. Toth, P. and Vigo, D. (2014) Vehicle Routing: Problems, Methods, and Applications. Siam. https://doi.org/10.1137/1.9781611973594
- 3. Song, Z.H., et al. (2015) Algorithm for Distance Constrained Aerial Vehicle Routing Problem: Based on Minimum Spanning Tree and Genetic Computation. 2015 11th International Conference on Computational Intelligence and Security (CIS), IEEE. https://doi.org/10.1109/CIS.2015.10
- 4. Rivera, J.C., Afsar, H.M. and Prins, C. (2016) Mathematical Formulations and Exact Algorithm for the Multitrip Cumulative Capacitated Single-Vehicle Routing Problem. European Journal of Operational Research, 249, 93-104. https://doi.org/10.1016/j.ejor.2015.08.067
- 5. Novoa, C. and Storer, R. (2009) An Approximate Dynamic Programming Approach for the Vehicle Routing Problem with Stochastic Demands. European Journal of Operational Research, 196, 509-515. https://doi.org/10.1016/j.ejor.2008.03.023
- 6. Bertsekas, D.P. (2014) Abstract Dynamic Programming. Tsinghua University Press, Beijing, 1-25.
