Operations Research and Fuzziology
Vol.08 No.03(2018), Article ID:26013,7
pages
10.12677/ORF.2018.83011
Reliability Assessment of Safe Driving Based on Multi-State Driving Environment
Kun Shi, Yongjin Zhang, Chaoyong Sun
School of Mathematics and Physics, Anhui University of Technology, Ma’anshan Anhui

Received: Jul. 2nd, 2018; accepted: Jul. 12th, 2018; published: Jul. 20th, 2018

ABSTRACT
The driving environment directly affects the perception, judgement and operation of vehicle drivers. First, through the analysis of the influencing factors of safety driving factors, the influence factors are divided into six aspects. Then, the weight of each factor is calculated by the analytic hierarchy process (AHP), and the factors are divided into multiple states and the factor state table is formulated. The membership degree of the measured values is allocated by the fuzzy mathematics membership function, the fuzzy matrix of membership degree is constructed, and the safety driving reliability is calculated based on the factor weight and the fuzzy matrix method. Finally, taking the safe driving in sunny weather in the daytime as an example, the analysis shows that the fuzzy analytic hierarchy process (AHP) is effective in evaluating the safety driving reliability.
Keywords:Multi State Environment, Analytic Hierarchy Process, Membership Function, Fuzzy Matrix, Reliability
基于多状态驾驶环境的安全驾驶可靠度评估
石坤,张永进,孙超勇
安徽工业大学数理学院,安徽 马鞍山

收稿日期:2018年7月2日;录用日期:2018年7月12日;发布日期:2018年7月20日

摘 要
行车环境直接影响汽车驾驶者的感知、判断、操作。首先,通过对影响安全驾驶因子的分析,将影响因子分为六个方面,然后,应用层次分析法计算各因子的权重,对影响因子进行多状态划分并制定因子状态表。利用模糊数学隶属函数对实测值进行隶属度分配,构造隶属度模糊矩阵,基于因子权重与模糊矩阵方法计算安全驾驶可靠度。最后,以白天天气晴朗环境下安全驾驶为实例,分析表明了应用模糊层次分析法对安全驾驶可靠度评估的有效性。
关键词 :多状态环境,层次分析法,隶属函数,模糊矩阵,可靠度

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
外部环境作为影响人机系统可靠性的因素,对安全驾驶有着至关重要的作用。如交通法规用来约束驾驶行为保证汽车安全驾驶;外部温度影响人体操作的灵敏度和反应能力等。目前在对汽车安全驾驶的研究中,国内外学者较偏向于对人的可靠性的研究,忽视对外部环境的研究。调查显示在交通安全事故中与人相关的比例为40%,与车辆相关比例25%,与环境相关比例35%,可知环境在安全驾驶方面的作用。而在对环境的研究中也只是进行单因素的分析:徐锦强等 [1] 针对车道变换分析驾驶可靠性;侯明哲等 [2] 建立跟驰状态下可靠性模型;陈国柱等 [3] 对冰雪路面进行分析。针对研究学者的单一性,本文主要通过分析各因子,综合研究环境可靠性。
2. 评价因子与权重确定
2.1. 评价因子
汽车驾驶需要从外部不间断的感知、判断,外部环境的改变意味着判断的差异与操作的差异,文章主要对道路交通法规、路况、车速、温度、照明、可视距离等评价因子进行分析。
1) 道路交通法规
道路交通法规是由国家制定并施行的约束驾驶人行为,保障行车安全的有关规定。交通法规对维持道路畅通、保持车辆有序规范行驶和避免人民生命财产损失等方面都发挥着重要作用。按照驾驶人对道路交通法规是否遵守和遵守程度对其进行分级,1代表驾驶人严格遵守,0代表无视法规。
2) 路况
路况可以分为路面拥挤度和路面摩擦系数。路面拥挤度是衡量路面的拥堵状况,路面畅通有利于保持良好视野,避免汽车追尾和舒适的驾驶情绪。路面拥挤度依据交通指数进行分级,交通指数 [4] 是用从0到10来衡量交通道路畅通情况。路面摩擦系数是指路面的粗糙度,过于光滑的路面会导致汽车驾驶时出现车辆打滑、刹车距离过远等的现象,而车辆打滑、刹车距离过远对交通安全的影响是巨大的。我国道路正常干燥沥青路面的摩擦系数为0.6,雨天路面摩擦系数降为0.4,雪天则为0.28,结冰路面就更低,只有0.18。
3) 车速
由于驾驶人对刺激的追求,超速行驶酿成的交通事故频频发生。车速过高给人一种兴奋感,而当人处于兴奋状态下,对于事物的判断会出现偏差,同时车速过高影响人的反应时间和紧急刹车制停的距离,导致交通事故。对于每条道路都会限制最高车速,保障行车安全。
4) 温度
温度是最容易被人体所感知,温度的变化直接对人的生理、心理产生影响。温度过低会使人的肢体僵化,降低人的操作的灵敏度,温度过高会使人出现胸闷、烦躁等不良的情绪。无论是温度过高或过低都影响驾驶汽车的安全性,最适宜人体的温度是在15℃~25℃。
5) 照明
眼睛作为最重要的感知器官之一,通过对光线的捕捉来获取外部的信息。当人长期处于光照强度过低的环境工作时,眼睛会出现视觉疲劳,直接影响人的精神状态,可能出现注意力不集中,瞌睡等不良反应;光照过强或光线直射时,直接降低人眼的分辨能力。当照明度在100~1000 lx逐渐提高时,视力也会相应的提高。
6) 可视距离
可视距离指人眼可以辨识的距离,可视距离会因天气状态、车流量而改变,天气晴朗时可视距离足够大,驾车可靠性比较高,而当出现雾霾或暴雨时,可视距离会大幅下降,使人无法准确获取外部信息,且对于紧急事情来不及反应。
2.2. 因子权重确定
各个影响因子对安全驾驶的重要度存在着差异,为分析各个因子的差异,采用层次分析法 [5] 计算各个因子的权重。
1) 建立递阶层次结构
依据传统人机系统三阶段 [6] (感知、判断、操作)模型来建立递阶层次结构,如图1。
2) 构造判断矩阵并赋值
构造判断矩阵的方法是:每一个具有向下隶属关系的元素(被称作准则)作为判断矩阵的第一个元素(位于左上角),隶属于它的各个元素依次排列在其后的第一行和第一列。例如图2,A层与B层的判断矩阵(B层具有相同重要度)。同理对B层、C层列出判断矩阵,分别如图2~5。
3) 计算因子权重

Figure 1. Hierarchical structure diagram
图1. 层次结构图

Figure 2. Judgment matrix
图2. 判断矩阵

Figure 3. Judgment matrix
图3. 判断矩阵
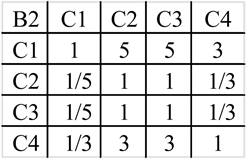
Figure 4. Judgment matrix
图4. 判断矩阵

Figure 5. Judgment matrix
图5. 判断矩阵
依据判断矩阵用归一法将各个因子的权重进行计算并汇总,分别如下:
 ,
,
 ,
,

各因子权重表示为:
4) 因子状态分类表的制定
依据上面各个因子的特征对因子进行多状态分类:很可靠、可靠、相对可靠、不可靠、很不可靠。分类表如表1。
3. 隶属函数确定与计算可靠度
3.1. 隶属函数
隶属函数 [7] 是用来刻画值所在区间的分布概率,即值的隶属度。隶属函数的种类很多,常见的有矩形分布、梯形分布、高斯分布、柯西分布、K次抛物型分布。文章采用最适用的梯形分布来确定隶属度。具体函数如下:
Table 1. Factor and state classification table
表1. 因子及状态分类表
式中:u1,u2,u3,u4,u5因子等级表中各个等级所对应的阈值,y为实际值。
3.2. 计算可靠度
1) 列出模糊矩阵
依据隶属函数和状态分类表算出实际值在区间的隶属度,用隶属度来构造模糊矩阵V
式中vi1表示第i种因子所在1等级的程度,即是i因子在等级上的隶属度。
2) 将因子权重与模糊矩阵结合求解
(1)
式中: 表示数学模糊算子,常见的模糊算子有:“Min-Max”模糊算子、“积–和”模糊算子、“Min/积–和”模糊算子、“Min-积”模糊算子、“Min-和”模糊算子,这里表示实数的积–和算子。
4. 实例分析
以白天天气晴朗环境下为例,确定各个因子的所在等级,一般情况人们都能够很好的遵守交通法规,交通指数处于通畅状态,一般道路的摩擦系数在0.6以上。具体相关数据如表2。
依据数据代入相应隶属函数求出模糊矩阵:
Table 2. Factor data
表2. 因子数据
将A、V代入(1)中求出
依据最大隶属度原则环境对驾驶行为影响处于可靠状态,驾驶行为可靠性有待进一步提升。严格遵守交通道路法规,不同道路、不同天气采取不同车速行驶,遇到交通道路堵塞时戒骄戒躁等都能有效提升驾驶行为可靠度。
5. 结论
1) 驾驶人在严格遵守交通法规,注意实时路况,限制适当车速,依据照明和可视距离调整驾车方案的情况下都能够很好保障可靠的驾驶行为。
2) 模糊评估法能够很好的将难以量化分析的因素进行量化,近似地对因素进行评估,是处理复杂多变因素的有效方法。同时,模糊评估法虽然可以对因素进行量化,但是也具有主观性强,分析结果因人而异的缺点,不能做到对因素的精确评估。
基金项目
安徽工业大学研究生创新基金项目(基金编号:2016138);教育部人文社会科学研究规划基金项目(基金号:17YJA630135);安徽省自然科学基金(基金号:1808085MG220)。
文章引用
石 坤,张永进,孙超勇. 基于多状态驾驶环境的安全驾驶可靠度评估
Reliability Assessment of Safe Driving Based on Multi-State Driving Environment[J]. 运筹与模糊学, 2018, 08(03): 83-89. https://doi.org/10.12677/ORF.2018.83011
参考文献
- 1. 徐锦强, 陈竹师, 丁艺. 基于驾驶行为的车道变换模型研究及仿真[J]. 华东交通大学学报, 2011, 28(6): 68-72.
- 2. 侯明哲, 罗阳明, 佟禹. 跟驰状态下驾驶人安全可靠度模型[J]. 公路, 2014(8): 70-74.
- 3. 陈国柱, 莫宣艳, 毛程远. 冰雪条件下城市道路交通安全评价方法研究[J]. 交通运输系统工程与信息, 2011, 11(60): 130-134.
- 4. 孙小菲, 陈旭梅, 高永. 计量经济学的交通指数与公交指数关联性分析[J]. 哈尔滨工业大学学报, 2016, 48(3): 60-65.
- 5. 邓雪, 李家铭, 曾浩健, 陈俊羊, 赵俊峰. 层次分析法权重计算方法分析及其应用研究[J]. 数学的实践与认识, 2012, 42(7): 93-100.
- 6. 裴玉龙, 马艳丽. 疲劳对驾驶员感知判断及操作特性的影响[J]. 吉林大学学报(工学版), 2009, 39(5): 1151-1156.
- 7. 陈铭, 李红燕, 王铁宁. 模糊综合评判中非线性隶属函数的确定[J]. 数学的实践与认识, 2006, 36(9): 124-128.
