Operations Research and Fuzziology
Vol.
09
No.
01
(
2019
), Article ID:
28283
,
8
pages
10.12677/ORF.2019.91002
Finite Time Stable Predictive Control for Discrete Systems
Shuang Zhang, Xiaohua Liu
Ludong University, Yantai Shandong

Received: Dec. 8th, 2018; accepted: Dec. 21st, 2018; published: Dec. 28th, 2018

ABSTRACT
The finite-time stable predictive control problem for a class of discrete-time linear time-invariant systems is studied. The concept of finite-time stability is introduced into predictive control, and the relationship between finite-time stability and predictive control is established by the state feedback. The minimization optimization problem in finite time domain is transformed into a constrained problem with linear matrix inequalities by constructing the Lyapunov function. The sufficient conditions for the existence of state feedback control rate are given by using linear matrix inequalities. The numerical simulation results show the effectiveness of the proposed method.
Keywords:Model Predictive Control, Finite-Time Stability, State Feedback, Linear Matrix Inequality
离散系统有限时间稳定预测控制
张 双,刘晓华
鲁东大学,山东 烟台

收稿日期:2018年12月8日;录用日期:2018年12月21日;发布日期:2018年12月28日

摘 要
针对一类离散时间线性时不变系统,研究其有限时间稳定预测控制问题。将有限时间稳定的概念引入预测控制中,借助状态反馈,建立有限时间稳定与预测控制之间的联系。通过构造Lyapunov函数将有限时域的最小化优化问题转化为具有线性矩阵不等式的约束问题,采用线性矩阵不等式的方法,给出状态反馈控制率存在的充分条件。数值仿真结果验证了所提出方法的有效性。
关键词 :模型预测控制,有限时间稳定,状态反馈,线性矩阵不等式

Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在控制系统的研究分析中,稳定性是最基本也是最重要的问题,所以近些年来稳定性成为国内外许多学者们研究的科研重点。在对控制系统进行稳定性分析时,其中应用较为广泛的Lyapunov稳定,BIBO稳定等稳定性概念关注的是无限时间区间内的系统行为 [1] 。但在实际应用中,人们关注的是系统在某一有限时间区间内的暂态行为。为了满足系统在有限时间内达到稳定的性能,20世纪60年代,Weiss和Infante首次提出了针对短时间稳定性(即有限时间稳定性)的概念,文献 [2] 总结了有限时间稳定控制的发展历程,提出了线性、非线性以及随机系统有限时间控制问题的分析和设计方法。文献 [3] 给出了有限时间稳定最优反馈控制的定义,提出使系统部分状态有限时间稳定的最优反馈控制器的设计方法。文献 [4] 针对线性时变系统输出反馈有限时间控制问题给出了有限时间稳定的充分条件。文献 [5] 针对线性系统有限时间稳定鲁棒控制问题,引入线性矩阵不等式方法,提出了状态反馈有限时间镇定控制算法。文献 [6] 针对含外部扰动的线性系统,提出使闭环系统有限时间有界的状态反馈控制器的设计方法,文献 [7] 针对网络系统,设计了系统有限时间鲁棒稳定控制器。有限时间稳定的概念还被推广到 控制 [8] 、容错控制 [9] 、随机控制 [10] 等。
预测控制是一类应用广泛的先进控制算法,其稳定性一直是学术界关注的热点 [11] ,但针对有限时间稳定的预测控制的研究并不多见。
本文研究离散系统有限时间稳定的预测控制问题,给出状态反馈预测控制器的设计方案。基于线性矩阵不等式方法,研究优化问题可行解存在的条件,证明优化问题在给定的初始条件下闭环系统是有限时间稳定的。通过仿真实验验证所提方法的有效性。
2. 问题描述
考虑如下一类离散时间线性时不变系统:
(1)
其中, 为系统的状态, 为系统的初始状态, 为控制输入, 为系统输出, , 及 为相应维数的常数矩阵。
对于系统(1),选择有限时域优化性能指标为
(2)
其中,给定的加权矩阵 、 。 是 时刻的状态预测值, 是 时刻使性能指标最小的控制信号, 为控制时域。
本文的目的是针对系统(1),设计含预测的状态反馈控制器
(3)
保证系统在有限时间内趋于稳定。
结合(1)式和(3)式,得闭环系统
(4)
在控制区域 内选择如下Lyapunov函数 ,同时加入终端等式约束 ,则有 。
不妨假设,在每一采样时刻 ,有
将上述不等式从 叠加到 从而得到:
(5)
此时可知, 为性能指标 的一个上界,由此可将求性能指标最小化问题进一步转化为对上界 的最小化问题。
定义1 [12] :如下离散时间线性时不变系统
(6)
满足 是有限时间稳定的,如果 时,有 成立。
其中: 是常数矩阵, 是系统状态, 是系统的初始状态。 为给定常数 , 为给定正定矩阵, 为给定的正整数。
定义2:对于系统(1)及闭环系统(4),给定正常数 、 ( )和正定矩阵 ,当 时,都有 成立,则称闭环系统(4)是关于 是有限时间稳定的。
引理1 [12] :系统(6)有限时间稳定等价条件
1) 系统(6)关于 是有限时间稳定的
2) 对于 , 成立
3) 对于 ,若 ; 。
则 ;
4) 对于 ,存在对称矩阵值函数
满足: , ; ; 。
引理2 [13] :考虑对称矩阵
,其中 是方阵。
以下三个条件是等价的:
1) ;
2) , ;
3) , 。
3. 有限时间稳定状态反馈
解决有限时间稳定预测控制问题的关键在于寻找一个共同的状态反馈 。建立有限时间稳定与单值预测控制 [14] 之间的联系。
定理1:对于离散线性系统(1),要求 , ,求得闭环系统的稳定性取决于状态反馈 。假设存在可逆矩阵 ,使得 为正定矩阵,存在矩阵 及标量 使得
(7)
(8)
其中, ,
,
那么系统在控制器 的作用下,关于 是有限时间稳定的,并且满足性能指标。
证明:我们假设 ,要证明当 时有 。
选择Lyapunov函数 ,对于标量 ,
有,
通过迭代我们可以获得: (9)
令
有,
(10)
(11)
根据(9)~(11),可得
进而有
令 ,我们有
利用Schur补有
左右同乘对称矩阵
得:
令 ,同时 ,此时有 ,即为所求的增益矩阵。
根据定理1,状态反馈有限时间稳定预测控制算法如下:
步骤1:给定矩阵 ,常数 ,预测时域 ;
步骤2:在每一个采样时刻 ,测量系统的状态 ;
步骤3:在每一个采样时刻 ,求解优化问题(7)~(8),根据定理1进而得到有限时间稳定预测控制中的反馈增益 ;
步骤4:将所求的控制序列 作用到被控系统(1),测量闭环系统(4)的状态 及输出 ;
步骤5:令 ,返回到步骤2。
4. 仿真案例
对于离散时间线性系统,选取系统参数如下:
, , 。
选取初始状态 , , , , 。性能指标的加权矩阵为 , ,采样间隔为1 s。
按照本章提出的有限时间稳定预测控制算法,运用Matlab中的LMI (线性矩阵不等式)进行求解,进而获得满足条件的状态反馈预测控制器。仿真案例如下:
图1体现了系统在 区间内的状态运动轨迹表明了系统的状态是有界的。
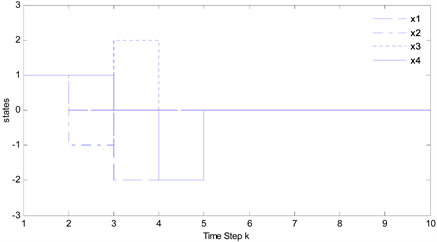
Figure 1. States of the closed-loop system
图1. 闭环系统状态轨迹
图2及图3表明了系统的输入和输出在给定的有限时间区间内均无较大超调。
图4表明在控制器(3)的作用下,系统在 时间内,只要系统初始值满足 ,闭环系统的轨迹则满足 ,则闭环系统(4)关于 是有限时间稳定的。
图5表明系统的性能指标最终在 趋于稳定。
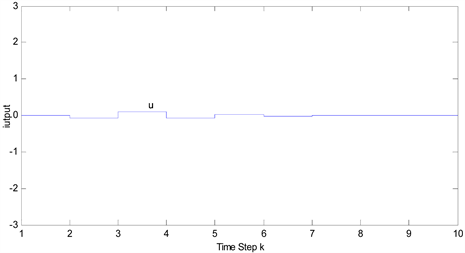
Figure 2. The trajectory of the control input
图2. 控制输入轨迹

Figure 3. Output of the closed-loop system
图3. 闭环系统的输出轨迹

Figure 4. The trajectory of x’Rx
图4. x’Rx轨迹
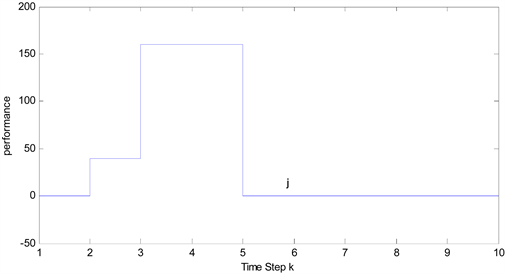
Figure 5. Performance index change
图5. 性能指标变化情况
5. 总结
本文针对一类离散线性系统,给出有限时间稳定预测控制的定义,为使系统在有限时间内性能指标在线最小化,设计状态反馈控制器,通过求解线性矩阵不等式给出满足条件的矩阵,给出闭环系统满足的条件。仿真结果给出算法的可行性。
致谢
感谢导师刘晓华老师对我的悉心指导和耐心帮助。刘老师非常关心我的学业进展,老师严谨的科研态度深深感染着我, 经常教导我们做科研一定要认真严谨。不仅如此,刘老师在生活中也经常教导我, 从老师身上学到了很多为人处世的道理,令我受用终身。
文章引用
张双,刘晓华. 离散系统有限时间稳定预测控制
Finite Time Stable Predictive Control for Discrete Systems[J]. 运筹与模糊学, 2019, 09(01): 6-13. https://doi.org/10.12677/ORF.2019.91002
参考文献
- 1. Xue, W.P. and Mao, W.J. (2013) Asymptotic Stability and Finite-Time Stability of Networked Control Systems: Analysis and Syn-thesis. Asian Journal of Control, 15, 1376-1384.
- 2. Dorato, P. (2005) An Overview of Finite-Time Stability. Current Trends in Nonlinear Systems and Control. Birkhauser Boston, 185-194.
- 3. Haddad, W.M. and Lafflitto, A. (2015) Finite-Time Partial Stability and Stabilization and Optimal Feedback Control. Journal of the franklin Institute, 6, 2329-2357. https://doi.org/10.1016/j.jfranklin.2015.03.022
- 4. Amato, F., Ariola, M. and Cosentino, C. (2010) Finite-Time Control of Discrete-Time Linear Systems: Analysis and Design Conditions. Automatica, 46, 919-924. https://doi.org/10.1016/j.automatica.2010.02.008
- 5. Amato, F., Arioa, M. and Cosentino, C. (2001) Finite-Time Control of Linear Systems Subject to Parametric Uncertainties and Disturbances. Automatica, 37, 1459-1463. https://doi.org/10.1016/S0005-1098(01)00087-5
- 6. 沈艳军. 一类线性离散时间系统有限时间控制问题[J]. 控制与决策, 2008(23): 107-109.
- 7. Wang, L.M., Shen, Y. and Sheng, Y. (2016) Finite-Time Robust Stabilization of Uncertain Delayed Neural Networks with Discontinuous Activations via Delayed Feedback Control. The Official Journal of the International Neural Network Society, 76, 46-54. https://doi.org/10.1016/j.neunet.2016.01.005
- 8. 严志国, 张国山. 线性随机系统有限时间 控制[J]. 控制与决策, 2011, 26(8): 1224-1228.
- 9. Gao, M.Z., Cai, G.P. and Nan, Y. (2016) Finite Time Fault-Tolerant Control for Flutter of Wing. Control Engineering Practice, 51, 26-47. https://doi.org/10.1016/j.conengprac.2016.03.007
- 10. Gao, W.H., Deng, F.Q., Zhang, R.Q. (2014) Finite-Time Control for Time-Delayed Stochastic Systems with Markovian Switching. Hindawi Publishing Corporation, 1-10.
- 11. 席裕庚, 耿晓军, 陈虹. 预测控制性能研究的新进展[J]. 控制理论与应用, 2000, 17(4): 469-475.
- 12. Amato, F. and Ariola, M. (2005) Finite-Time Control of Discrete-Time Linear Systems. IEEE Transactions on Auto-matic Control, 50, 724-729. https://doi.org/10.1109/TAC.2005.847042
- 13. Yza, E.E. (1998) Linear Maxtrix Inequalities in System and Control Theory. Proceeding of the IEEE, 86, 2473-2474. https://doi.org/10.1109/JPROC.1998.735454
- 14. 袁璞, 左信, 郑海涛. 状态反馈预估控制[J]. 自动化学报, 1993, 19(5): 569-576.