Operations Research and Fuzziology
Vol.
10
No.
02
(
2020
), Article ID:
35037
,
17
pages
10.12677/ORF.2020.102013
New Numerical Methods for Robust Regularization Problem Based on Alternating Direction Method of Multipliers
Fengrui Ji, Jie Wen*
College of Science, Nanjing University of Aeronautics and Astronautics, Nanjing Jiangsu

Received: Mar. 25th, 2020; accepted: Apr. 8th, 2020; published: Apr. 15th, 2020

ABSTRACT
Linear regression is an important model in machine learning, but too large data will make the linear regression model fall into over-fitting problem. Regularization is the main method to solve the over-fitting problem. The standard regularization model is the method that linear regression co-operates with regularization to ensure the quality of classification and reduce the risk of falling into over-fitting. However, the classifier obtained by the standard regularization model will be unstable when the training samples are disturbed. To solve this problem, we propose two kinds of robust regularization models: 1) Stochastic robust regularization: combining the expectation of residual with the regularization; 2) Worst case robust regularization: combining the worst case residual with the regularization. Then, we use Alternating Direction Method of Multipliers (ADMM) algorithm to get the optimal solution of the robust regularization model. Numerical experiments show that the classifiers obtained by stochastic and worst-case robust regularization have good robustness when training disturbed data sets, but the classifiers obtained by standard regularization method fluctuate greatly.
Keywords:Linear Regression, Regularization, ADMM, Robustness

基于ADMM算法的鲁棒正则化问题求解方法
吉锋瑞,文杰*
南京航空航天大学理学院,江苏 南京

收稿日期:2020年3月25日;录用日期:2020年4月8日;发布日期:2020年4月15日

摘 要
线性回归是机器学习中的重要模型,但是过大的数据量会使线性回归模型陷入过拟合。正则化技术是解决过拟合问题的主要方法。标准的正则化模型是运用线性回归项和正则项协同作用以达到保证分类质量和降低陷入过拟合风险的目的。但是当训练样本存在扰动时,标准的正则化模型得到的分类器会因为数据集存在扰动而表现得不稳定。针对该缺点,本文提出了两种鲁棒正则化模型:1) 随机鲁棒正则化:将残差的数学期望和正则项结合;2) 最坏情况鲁棒正则化:将最坏情况的残差和正则项结合。然后利用交替方向法(交替方向法,ADMM)求得鲁棒正则化模型的最优解。数值实验显示:当训练存在扰动的数据集时,随机鲁棒正则化和最坏情况鲁棒正则化得到的分类器具有很好的鲁棒性,而标准正则化方法得到的分类器波动很大。
关键词 :线性回归,正则化,ADMM,鲁棒性

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 介绍
分类问题是机器学习中一类重要的问题。很多分类模型都可以很好地解决分类问题,其中线性回归就是一类重要的分类模型。线性回归 [1] 的数学模型如下:
(1.1)
其中 和 是训练样本的数据, 是回归系数。由于目标函数是凸函数,所以该问题是凸优化问题。当 时,该问题的最优值是0。在绝大部分时候,模型通过训练数据集学习经验或者知识时,得到的最优值往往不是0,即 。所以 时的问题是非常有实用意义的。线性回归能够以较快的速度做出较高质量的预测,所以它被人们广泛地应用于各个领域。 [2] 通过多元线性回归模型分析了影响武汉市水资源承载力的主要因素, [3] 通过线性回归模型讨论了温度与月售电量的关系, [4] 通过线性回归模型分析了影响全国粮食产量的因素,得到了线性回归方程,并发现该方程具有较高的准确度。
当训练样本的维数远远小于训练样本的数据量时,模型(1.1)容易陷于过拟合。过拟合问题是模型(1.1)过分学习训练样本的经验或者知识,将训练样本的特殊特征作为普遍特征。它的表现形式是模型(1.1)训练得到的结果在训练集上表现很好,但是在测试集上表现不佳。正则化技术是解决过拟合问题的常用方法。正则化模型如下:
(1.2)
其中 是正则项, 为保真项, 是正则项参数。正则项参数平衡了残差保真项 和正则项 的关系。 较小时,残差较小,分类准确率高,但是陷入过拟合的风险也就相对较大。 较大时,模型泛化能力会有所增强,但是残差较大,导致分类准确率较低。所以选择一个合适的 是很重要的。当 是凸函数时,问题(1.2)是凸优化问题。常见的凸正则项有LASSO [5] 、Fused LASSO [6] 、Elastic Net [7] 、L2正则项 [8] 等等。由于它们都是凸优化问题,所以有很多优化方法求得最优解。正则项函数不仅仅局限于凸函数,常见的非凸正则项函数有MCP模型 [9] 、SCAD模型 [10] 、桥回归模型 [11] 等等。由于这些模型都是非凸优化问题,所以求解较为困难,研究的相对较少。
当正则项函数是L1范数,度量残差 的范数是L2范数时,问题(1.2)就是LASSO问题。由于L1范数会压缩回归系数,所以LASSO问题的回归系数具有稀疏性。LASSO问题如(1.3):
(1.3)
平衡了模型的分类准确率和回归系数的稀疏度。 较大时,回归系数的稀疏度较大但是分类准确率较低。 较小时,分类准确率较高,但是回归系数的稀疏度较低,所以选择合适的 相当重要。另外具有稀疏性的模型能够很好地对数据进行拟合,并且计算简单,所以被人们广泛地应用多个领域。随着人们对该领域的深入研究,发现押注稀疏性原理 [12]:既然无法处理有效稠密问题,倒不如在稀疏问题上寻找有效的处理方法。由于L1正则项是凸函数并且能够保证回归系数具有稀疏性,所以被很多机器学习的模型用来解决过拟合问题。但是模型(1.3)在遇到存在扰动的数据时会陷入麻烦。对训练样本加100个随机扰动,每个扰动的幅度都是训练样本10%。模型(1.3)通过训练原始训练样本求得一组回归系数。将求得的回归系数通过线性回归模型预测存在扰动的数据集类别,得到一组分类准确率。这组分类准确率构成一组数组,绘成图1。

Figure 1. Training results of Model (1.3) when the training samples are disturbed
图1. 当训练样本存在扰动时,模型(1.3)训练结果
通过图1发现当数据存在扰动时,LASSO问题的分类准确率波动很大。最高分类准确率与最低分类准确率之差大约有30%。由此可以看出,当数据集存在一定波动时,LASSO问题的训练结果受到较大影响。
以L1正则项为例,发现标准的正则化方法不能够很好地训练受到扰动的训练样本。为了解决这个问题,本文提出了两种鲁棒正则化模型解决训练样本存在扰动的问题(本文所使用的正则项是L1正则项、L2正则项、L1-L2正则项和Huber正则项)。第一种模型是利用概率论的方法建立随机鲁棒正则化模型。
该模型认为扰动是随机变量,所以控制拟合效果的方法由传统的 替换为 。通过调整正则项参数平衡 和正则项之间的关系。第二种模型是通过定义最坏情况的误差建立最坏情况
鲁棒正则化模型。该模型保障拟合效果的方法是考虑最坏情况下的残差。同样设定合理的正则项参数可以平衡最坏情况的残差和正则项。当正则项是L1、L2、L1-L2正则项时,本文将鲁棒正则化模型分为两块优化问题进行求解。当正则项是Huber正则项时,本文将鲁棒正则化模型分为三块优化问题进行求解。数值实验显示鲁棒正则化模型能够保证分类准确率的同时也具有较强的鲁棒性。另外,数值实验还说明了鲁棒Huber正则化和L1-L2正则化模型分类准确率表现优于鲁棒L1、L2正则化模型。
本文的内容安排如下:第二章介绍正则化方法;第三章介绍两块ADMM算法和三块ADMM算法;第四章介绍随机鲁棒逼近正则化以及求解方法;第五章介绍最坏情况鲁棒正则化模型以及求解方法;第六章通过数值试验比较了鲁棒正则化方法和标准正则化方法;第七章对本文做出总结。
2. 基础知识
在大数据时代,数据的规模是十分巨大的。过大的数据量容易使机器学习中的模型陷入过拟合困扰。该模型会过分学习训练集上的知识,从而认为特殊性质就是普遍性质。正则化方法通过添加正则项的方法来降低模型陷入过拟合的风险。本文将介绍正则化方法以及常见的正则项。
2.1. 正则化方法
一般正则化模型如下:
(2.1)
其中 度量了残差 的大小,g从某种意义上度量了x的大小, 是正则项参数。正则项参数平衡了保真项 和 。本文所使用的正则项函数g都是凸函数,所以(2.1)是凸优化问题。引入变量y,令 ,问题则转化为等式约束下可分的优化问题:
(2.2)
该问题的拉格朗日函数为:
(2.3)
其中u是对偶变量, 是正则项参数。
性质1. 问题(2.1)的最优性条件是:
(2.4)
其中 是次微分算子。若正则项函数 是可导函数, 则是 。
2.2. L1正则化
当 时,模型(2.1)就是LASSO,模型如(2.5):
(2.5)
正则项参数 可以平衡分类准确率和回归系数的稀疏性。 较大时,回归系数较为稀疏,模型不易陷入过拟合,但是模型拟合效果较差。 较小时,则 较大时相反。LASSO回归有着广泛的应用, [13] 使用LASSO回归对垃圾邮件过滤, [14] 建立LASSO回归模型和计量经济学模型解释了实体金融市场与经济政策的内在关系, [15] 将LASSO回归应用于三波段红外火焰探测器的具体识别中。
2.3. L2正则化
当 时,模型(2.1)就是Ridge回归,模型如下:
(2.6)
正则项参数 可以平衡分类准确率和回归系数的规模。 较大时,回归系数规模较小,模型不易陷入过拟合,但是模型拟合效果较差。 较小时,则与之相反。 [16] 利用ridge回归分析了社会因素、经济因素以及政策制度因素对农地城市流转的影响, [17] 利用ridge回归研究了对外贸易和外商直接投资对人力资本存量的影响。
2.4. L1-L2正则化
当 时,模型如下:
(2.7)
其中正则化参数 ,。当 时,L1-L2正则化就是L1正则化,当 时,L1-L2正则化就是L2正则化。 越大,则回归系数越稀疏。如果希望回归系数规模较小,则适当调小 。这样可以选择合适的 通过控制 的大小控制回归系数的稀疏性和规模。另外,不难发现L1正则项对小残差灵敏和L2正则项对大残差灵敏,但是L1-L2正则项通过组合L1正则项和L2正则项的方法克服上述两个正则项的缺点。
2.5. Huber正则化
当 时,问题(2.1)就是Huber正则化。Huber正则化模型如(2.8):
(2.8)
其中,
(2.9)
Huber正则项是通过定义分段函数的方法克服L1范数、L2范数的缺点。该分段函数的特点是面对小误差时使用L2范数,面对大误差时使用L1范数,这与L1-L2正则项有本质不同,所以这两个正则项
不是一个正则项。由于 ,所以问题(2.8)等价于:
(2.10)
这是一个凸的不光滑优化问题,使用一些非光滑技术可以求解出该问题的最优解。
3. ADMM算法
ADMM是一种可以高效求解等式约束下可分结构的凸优化问题的算法。该算法由于在统计学习、图像处理等数据分析处理领域有着良好的表现而备受关注。本节将讨论两块ADMM算法和三块ADMM算法。
3.1. 两块ADMM算法
当优化分体分成两个整体时,模型可以表示为:
(3.1)
其中 ,。该问题的增广拉格朗日函数为:
(3.2)
其中 是对偶变量, 是增广拉格朗日乘子。ADMM算法子问题如下:
(3.3)
(3.4)
(3.5)
令 ,,上述子问题则转化为:
(3.6)
(3.7)
(3.8)
假设1 [18]. 假设 , (或者 , 的延伸函数)是闭凸真函数。
当 是真函数时,它的上图 非空且不包含竖直的直线。因此f是真函数等价于 是非空凸集,f是C上的有限函数。另外当 是闭函数时,则函数f对应的下水平集 是闭集。当 是凸函数时,则有 时, 。综上,满足假设1的 可以通过上图简洁表示,即 是非空闭凸集。假设1保证求解x和y的优化子问题存在最优解,即使 和 是不可导函数,也存在 和 极小化问题(3.6)和问题(3.7)。
假设2 [18]. L0存在鞍点。
鞍点存在等价于原问题存在最优解,对偶问题存在最优解,强对偶成立即原问题的最优值与对偶问题的最优值相同。如果凸优化问题满足Slater条件,则对偶问题存在最优解 且强对偶成立。所以加上原问题存在最优解就可以保证原问题存在鞍点。
定理1. 若优化问题(3.1)满足下述性质,则(3.1)存在鞍点:
1) 优化问题(3.1)是凸优化问题;
2) 满足Slater条件,即 ,使得 ,其中D是(3.1)的可行域;
3) 原始问题存在最优解。
通过定理1,可以判断出优化问题(3.1)是否存在鞍点,那么就可以验证假设2是否成立。当假设1和假设2成立时,定理2保证了ADMM算法的收敛性。
定理2 [18]. 假设1和假设2成立,则ADMM算法满足如下性质:
1) 残差收敛:当 时,有 ,其中 ;
2) 目标函数收敛:当 时,有 ;
3) 对偶变量收敛:当 时,有 ,其中 是对偶最优点。
3.2. 三块ADMM算法
当优化问题可以分成三块时,模型可以表示为:
(3.9)
其中 ,。该问题的增广拉格朗日函数为:
(3.10)
其中 是对偶变量, 是增广拉格朗日乘子。ADMM算法迭代算法如下:
(3.11)
(3.12)
(3.13)
(3.14)
文献 [19] 讨论三块ADMM算法的收敛性。三块ADMM算法不能够保证收敛,只有加强一些条件才能保证三块ADMM算法的收敛性。由于本文没有增加一些条件保证三块ADMM算法的收敛性,所以在进行数值实验的过程中三块ADMM算法在一些情况下不收敛。
4. 随机鲁棒正则化模型
当训练样本受到扰动时,标准正则化方法不能应对这种情况。从图1中可以发现标准的LASSO问题在这种情况下分类结果受到了较大的影响。为了增强分类模型的稳定性,本节利用概率论的方法提出随机鲁棒正则化模型。
4.1. 随机鲁棒正则化
随机鲁棒正则化模型如下:
(4.1)
其中 , 是均值为0的随机矩阵, 是随机变量 的期望, 是正则项参数。由于 和 是凸函数,所以问题(4.1)是凸优化问题。保真项 是训练受到扰动的数据时残差的期望。 是权衡保真项和正则项之间的关系。 越大,模型陷入过拟合的概率就越低,但也会牺牲模型的准确率。相反的, 较小时,分类准确率会很高,但是模型陷入过拟合的概率也会较高。由于 的导数难以计算,所以直接求解问题(4.1)过程繁琐。性质2可以将该问题转化为一个相对容易求解的问题。性质2如下:
性质2. 。
通过性质2,问题(4.1)则转化为:
 (4.2)
(4.2)
令x = y,问题则转化为:
 (4.3)
(4.3)
该问题的拉格朗日函数为:
 (4.4)
(4.4)
其中 是对偶变量。
是对偶变量。
性质3. 问题(4.1)的最优性条件:
 (4.5)
(4.5)
4.2. ADMM算法求解随机鲁棒正则化
上节已经说明随机鲁棒正则化模型等价如下问题:
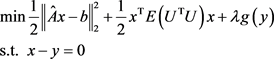 (4.6)
(4.6)
问题(4.6)的增广拉格朗日函数是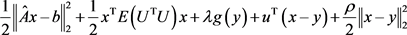 ,ADMM迭代算法如下:
,ADMM迭代算法如下:
 (4.7)
(4.7)
 (4.8)
(4.8)
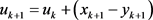 (4.9)
(4.9)
性质4. ADMM算法在求解问题(4.6)时算法是收敛的。
证明:令 ,
, 。易知
。易知 和
和 是闭凸真函数,所以问题(4.6)满足假设1。由于
是闭凸真函数,所以问题(4.6)满足假设1。由于 和
和 都是凸函数,所以问题(4.6)是凸优化问题。又因为
都是凸函数,所以问题(4.6)是凸优化问题。又因为 ,所以
,所以 ,有
,有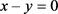 ,所以问题(4.6)满足Slater条件。
,所以问题(4.6)满足Slater条件。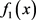 和
和 是闭凸真函数,所以原问题存在最优解
是闭凸真函数,所以原问题存在最优解 和
和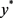 。综上,问题(4.6)满足假设2。由于问题(4.6)满足假设1,假设2,所以ADMM求解问题(4.6)时算法是收敛的。
。综上,问题(4.6)满足假设2。由于问题(4.6)满足假设1,假设2,所以ADMM求解问题(4.6)时算法是收敛的。
问题(4.7)存在解析解 。当
。当 时,易知问题(4.8)存在解析解
时,易知问题(4.8)存在解析解 。当
。当 时,利用分段讨论的方法可以得到问题(4.8)的解析解
时,利用分段讨论的方法可以得到问题(4.8)的解析解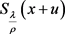 。
。
性质5. 当 时,问题(4.8)的解析解
时,问题(4.8)的解析解 。
。
证明:
Case 1. :
:

Case 2.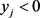 :
:

Case 3. :
:
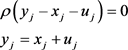
其中 的定义如下:
的定义如下:

同理,当 时,问题(4.8)的最优解是
时,问题(4.8)的最优解是 。
。
当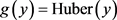 时,由(2.5)可知鲁棒Huber正则化方法等价于:
时,由(2.5)可知鲁棒Huber正则化方法等价于:
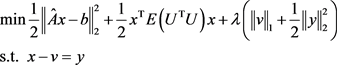 (4.10)
(4.10)
该问题的增广拉格朗日函数是
 (4.11)
(4.11)
该问题的ADMM子问题如下:
 (4.12)
(4.12)
 (4.13)
(4.13)
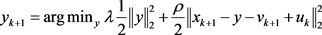 (4.14)
(4.14)
 (4.15)
(4.15)
问题(4.12)存在解析解 ,问题(4.13)存在解析解
,问题(4.13)存在解析解 ,问题(4.14)存在解析解
,问题(4.14)存在解析解 。以上问题使用的是三块ADMM算法,所以不能够保证算法是收敛的。
。以上问题使用的是三块ADMM算法,所以不能够保证算法是收敛的。
5. 最坏情况鲁棒正则化
随机鲁棒正则化是利用概率论的方法确定保真项,利用正则化的思想避免模型陷入过拟合问题。本节将从另外一个角度构造保真项,并以此为基础构造最坏情况鲁棒正则化。
5.1. 最坏情况鲁棒正则化
随机鲁棒逼近是利用概率论的方法描述训练样本的不确定,本节将利用定义最坏情况的方法描述训练样本的不确定性,定义最坏误差如下:
定义1. 最坏误差
 (5.1)
(5.1)
其中 是不确定集,即描述
是不确定集,即描述 所有情况的集合。由于范数是凸函数,所以任意不确定集
所有情况的集合。由于范数是凸函数,所以任意不确定集 的最坏误差都是凸函数。
的最坏误差都是凸函数。
最坏误差的定义刻画了训练样本的不确定。将最坏情况鲁棒逼近与正则项结合,构成最坏情况鲁棒正则化,模型如(5.2):
 (5.2)
(5.2)
其中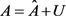 ,
, 是随机变量
是随机变量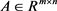 的期望。正则项
的期望。正则项 ,
, 是正则项参数,保真项
是正则项参数,保真项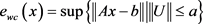 。
。 是最坏情况下的误差。
是最坏情况下的误差。 平衡最坏情况下的误差和正则项之间的关系。由于最坏误差和L1范数是凸函数,所以该问题是凸优化问题。由于讨论
平衡最坏情况下的误差和正则项之间的关系。由于最坏误差和L1范数是凸函数,所以该问题是凸优化问题。由于讨论 的所有情况过于复杂,所以本文讨论的最坏误差是
的所有情况过于复杂,所以本文讨论的最坏误差是 (
(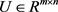 )。
)。
性质6. 在满足如下条件时,有 :
:
1) 向量 的范数是L2范数;
的范数是L2范数;
2) 矩阵U的范数是2范数;
3) 和
和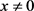 。
。
证明:

当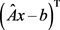 与
与 同向时,
同向时, 取到最大值
取到最大值 。
。
由于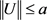 ,所以可知
,所以可知 。
。
综上, 。
。
根据性质6最坏情况的鲁棒正则化模型可以转化为:
 (5.3)
(5.3)
令x = y,模型(5.3)可以转化为:
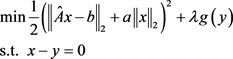 (5.4)
(5.4)
问题(5.4)的拉格朗日函数是 ,其中
,其中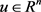 是对偶变量。通过拉格朗日函数可以得到问题(5.4)的最优性条件。
是对偶变量。通过拉格朗日函数可以得到问题(5.4)的最优性条件。
性质7. 问题(5.4)的最优性条件:
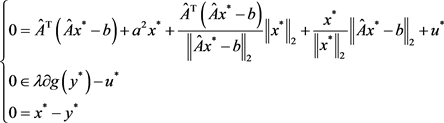 (5.5)
(5.5)
5.2. ADMM求解最坏情况鲁棒正则化
问题(5.4)的增广拉格朗日函数是 ,其中
,其中 是对偶变量,
是对偶变量, 是增广拉格朗日乘子。ADMM子问题如下:
是增广拉格朗日乘子。ADMM子问题如下:
 (5.6)
(5.6)
 (5.7)
(5.7)
 (5.8)
(5.8)
性质8. ADMM求解问题(5.4)时算法是收敛的。
证明:令 ,
, 。易知
。易知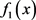 和
和 是闭凸真函数,所以问题(5.4)满足假设1.由于
是闭凸真函数,所以问题(5.4)满足假设1.由于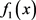 和
和 都是凸函数,所以问题(5.4)是凸优化问题。又因为
都是凸函数,所以问题(5.4)是凸优化问题。又因为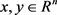 ,所以
,所以 ,有
,有 ,所以问题(5.4)满足Slater条件。
,所以问题(5.4)满足Slater条件。 和
和 是闭凸真函数,所以原问题存在最优解
是闭凸真函数,所以原问题存在最优解 和
和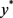 ,综上问题(5.4)满足假设2。由于问题(5.4)满足假设1,假设2,所以ADMM求解问题(5.4)时算法是收敛的。
,综上问题(5.4)满足假设2。由于问题(5.4)满足假设1,假设2,所以ADMM求解问题(5.4)时算法是收敛的。
令 ,有
,有
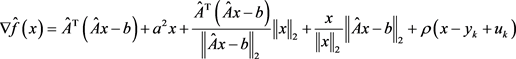 (5.9)
(5.9)
得到(5.6)的导数(5.9),可以利用很多经典的优化算法进行求解,但是大数据时代变量的维数和数据量会增加经典算法计算次数和存储空间。本文使用L-BFGS求解问题(5.6)的最优解。因为L-BFGS存储前m次迭代的少量数据,通过双回路递归的方法得到海塞阵逆矩阵的近似 ,所以会在一定程度上减少计算量。当
,所以会在一定程度上减少计算量。当 是L1正则项、L2正则项、L1-L2正则项时,问题(5.7)与问题(4.8)相同,此处不在赘述。当
是L1正则项、L2正则项、L1-L2正则项时,问题(5.7)与问题(4.8)相同,此处不在赘述。当 时,该问题等价于
时,该问题等价于
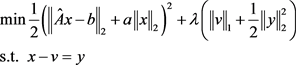 (5.10)
(5.10)
该问题的增广拉格朗日函数是 ,其中
,其中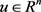 是对偶变量。该问题的ADMM子问题如下:
是对偶变量。该问题的ADMM子问题如下:
 (5.11)
(5.11)
 (5.12)
(5.12)
 (5.13)
(5.13)
 (5.14)
(5.14)
令 ,有
,有
 (5.15)
(5.15)
得到(5.11)的导数(5.15),利用L-BFGS可以求解出问题(5.11)的最优解 。通过分段讨论的方法,可
。通过分段讨论的方法,可
以求得问题(5.12)的解析解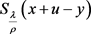 。由于问题(5.13)是光滑的凸优化问题,易知问题(5.13)存在解析解
。由于问题(5.13)是光滑的凸优化问题,易知问题(5.13)存在解析解 。
。
6. 数值试验
本节将描述训练数据得到的数值结果,模型在2.2 GHz Intel Core i7 CPU,16 GB RAM环境下进行训练。 ,
, 分别描述了ADMM算法对原始条件和对偶条件的可行性容忍程度。本文设置
分别描述了ADMM算法对原始条件和对偶条件的可行性容忍程度。本文设置 ,
, ,使用UCI的相关数据通过Python 3.7实现ADMM算法求解鲁棒正则化问题,所使用的数据如表1:
,使用UCI的相关数据通过Python 3.7实现ADMM算法求解鲁棒正则化问题,所使用的数据如表1:
Table 1. University of California Irvine Repository training data
表1. UCI Repository训练数据
本文使用的数据包括Heart,pop-failures,Austrian,Pima,spambase,Mushroom,a6a,shuttle,a9a,w8a,ijcnn1,Dota2。 ,其中
,其中 是
是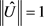 的随机矩阵。
的随机矩阵。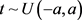 的随机变量,生成了100个U,这说明了存在振幅为a的扰动。通过ADMM算法求得结果见表2。
的随机变量,生成了100个U,这说明了存在振幅为a的扰动。通过ADMM算法求得结果见表2。
Table 2. Residual expectation
表2. 残差的期望
通过表2,可以发现当数据存在扰动时,标准的正则化方法已经不能够很好的解决分类问题,而鲁棒正则化模型能够较好地应对这种情况。由于L1正则项会压缩回归系数,所以L1正则化之后会导致分类准确率降低,残差增大。但是通过表2发现标准的L1正则化训练存在扰动的训练样本时表现竟然好于其它正则项。由此可以看出训练样本存在扰动时会破坏正则项一些较好的性质,让分类结果不尽人意。相比于标准的正则化模型,本文提出的鲁棒正则化模型不会破坏正则项的性质。通过表2,不难发现鲁棒L1-L2正则化、Huber正则化表现要优于L1正则化和L2正则化。另外,通过表2可以得到一个结论:随机鲁棒正则化的分类质量要优于最坏情况鲁棒正则化。导致这个结果的原因是两个模型考虑的因素不同,主要体现在随机鲁棒正则化模型的保真项是让残差的期望最小,而最坏情况鲁棒正则化的保真项是让最坏误差最小,所以随机鲁棒正则化残差的期望最小,分类结果最好。

Figure 2. Training results of w8a Huber regularization
图2. w8a Huber正则化训练结果
图2中sr表示的是标准正则化模型得到的残差曲线,srr表示的是随机鲁棒正则化模型得到的残差曲线,wcr表示最坏情况鲁棒正则化模型得到的曲线。通过图2,可以发现当扰动的振幅a = 0时,标准正则化的残差最小。随着振幅a的增大,标准正则化得到的残差明显增大不少,但是随机鲁棒正则化和最坏情况鲁棒正则化模型的残差增长速度缓慢。这意味着随机鲁棒正则化模型和最坏情况鲁棒正则化模型的抗干扰能力比标准正则化模型要强。另外由于随机鲁棒正则化考虑的是残差的期望最小,所以在图2中随机鲁棒正则化得到的残差之和要小于最坏情况鲁棒正则化。但是当振幅a增大到一定程度时,最坏鲁棒正则化的残差会小于随机鲁棒正则化。方差可以表示数据的波动情况,表3给出了残差的方差。
Table 3. Variance of residuals
表3. 残差的方差
通过表3的数据,可以发现标准的正则化方法得到残差的方差很大,鲁棒正则化模型得到残差的方差较小。表3说明标准的正则化方法得到的结果受到扰动的影响较大,在一些数据集上分类的波动是不能够被接受的。相反,鲁棒正则化模型得到的结果受到扰动的影响较小。由于最坏情况鲁棒逼近考虑的是优化最坏误差,所以收到扰动的影响最小,在一些样本集上训练结果波动几乎为0。随机鲁棒正则化模型只考虑残差的期望最小,所以受到扰动的影响介于标准正则化和最坏情况鲁棒正则化之间。
7. 总结
当训练样本存在扰动时,本文提出随机鲁棒正则化模型和最坏情况鲁棒正则化模型。利用ADMM算法求解上述模型,并将鲁棒正则化模型与标准正则化模型进行比较。通过比较发现本文提出的算法具有比标准正则化模型更好的抗干扰能力。数值实验显示:1) 本文提出的模型能够成功对抗存在扰动的训练样本;2) L1-L2正则项和Huber正则项表现优于L1正则项和L2正则项。
基金项目
国家自然科学基金青年科学基金项目:11701279。
文章引用
吉锋瑞,文 杰. 基于ADMM算法的鲁棒正则化问题求解方法
New Numerical Methods for Robust Regularization Problem Based on Alternating Direction Method of Multipliers[J]. 运筹与模糊学, 2020, 10(02): 122-138. https://doi.org/10.12677/ORF.2020.102013
参考文献
- 1. Boyd, S. and Vandenberghe, L. (2006) Convex Optimization. Cambridge University Press, Cambridge.
- 2. 陈威, 艾婵. 基于多元线性回归模型的武汉市水资源承载力研究[J]. 河南理工大学学报(自然科学版), 2017, 36(1): 75-79.
- 3. 薛斌, 程超, 欧世其, 等. 考虑舒适温度区间和突变量的月售电量预测线性回归模型[J]. 电力系统保护与控制, 2017, 45(1): 15-20.
- 4. 田秀芹. 基于多元线性回归的粮食产量预测[J]. 科技创新与应用, 2017(16): 3-4.
- 5. Tibshirani, R. (1996) Regression Shrinkage and Selection via the Lasso. Journal of the Royal Statistical Society: Series B (Methodological), 58, 267-288. https://doi.org/ 10.1111/j.2517-6161.1996.tb02080.x
- 6. Tibshirani, R. (2005) Sparsity and Smoothness via the Fused Lasso. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 67, 91-108. https://doi.org/ 10.1111/j.1467-9868.2005.00490.x
- 7. Hui, Z. (2005) Regularization and Variable Selection via the Elastic Net. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 67, 301-320. https://doi.org/ 10.1111/j.1467-9868.2005.00503.x
- 8. Tikhonov, A.N. (1977) Solution of Ill-Posed Problems. Winston, Washington DC.
- 9. Zhang, C.-H. (2010) Nearly Unbiased Variable Selection under Minimax Concave Penalty. The Annals of Statistics, 38, 894-942. https://doi.org/ 10.1214/09-AOS729
- 10. Zhang, H.H., Ahn, J., Lin, X., et al. (2006) Gene Selection Using Support Vector Machines with Non-Convex Penalty. Bioinformatics, 22, 88-95. https://doi.org/ 10.1093/bioinformatics/bti736
- 11. Frank, L.L.E. and Fridman, J.H. (1993) A Statistical View of Some Chemometrics Regression Tools. Technometrics, 35, 109-135. https://doi.org/ 10.1080/00401706.1993.10485033
- 12. Hastie, T., Tibshirani, R. and Wainwright, M. (2016) Statistical Learning with Sparsity: The Lasso and Generalizations. CRC Press, Boca Raton, FL. https://doi.org/ 10.1201/b18401
- 13. 徐征, 刘遵雄, 张贤龙. 基于套索(Lasso)的中文垃圾邮件过滤[J]. 华东交通大学学报, 2014(4): 130-135.
- 14. 孙昕. 基于Lasso方法的中国股市时滞性回归分析[D]: [硕士学位论文]. 大连: 大连理工大学, 2017.
- 15. 谭勇, 谢林柏, 冯宏伟, 等. 基于LASSO回归的红外火焰探测器的设计与实现[J]. 激光与红外, 2019, 49(6): 720-724.
- 16. 高魏, 闵捷, 张安录. 基于岭回归的农地城市流转影响因素分析[J]. 中国土地科学, 2007, 21(3): 51-58.
- 17. 罗良文, 阚大学. 对外贸易和外商直接投资对中国人力资本存量影响的实证研究——基于岭回归分析法[J]. 世界经济研究, 2011(4): 33-37.
- 18. Boyd, S., Parikh, N., Chu, E., et al. (2010) Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Foundations and Trends in Machine Learning, 3, 1-122. https://doi.org/ 10.1561/2200000016
- 19. Cai, X.J., Han, D.R. and Yuan, X.M. (2017) On the Convergence of the Direct Extension of ADMM for Three-Block Separable Convex Minimization Models with One Strongly Convex Function. Computational Optimization and Applications, 66, 39-73. https://doi.org/ 10.1007/s10589-016-9860-y
NOTES
*通讯作者。
