Hans Journal of Data Mining
Vol.07 No.04(2017), Article ID:22486,12
pages
10.12677/HJDM.2017.74011
Analysis of Influencing Factors of Fiscal Revenue in Zhejiang Province Based on Data Mining Technology
Liangliang Zhuang, Tong Wu
School of Mathematics and Information Science, Wenzhou University, Wenzhou Zhejiang
Received: Sep. 30th, 2017; accepted: Oct. 19th, 2017; published: Oct. 27th, 2017

ABSTRACT
Finance is the basis of governments to perform their functions whose basic responsibilities are the resource integration, resource reallocation and macroeconomic regulation and control. Besides, finance reflects the level of the development of social and economic to a great degree. This is why, to our country, enhancing the predict accuracy of finance means a lot. In order to accomplish this task, we analyzed the factors of influencing Zhejiang Province’s fiscal revenue, used best subset selection, forward stepwise selection, backward stepwise selection, ridge regression and Lasso regression respectively by using R software. We also give evaluation efficiency of each model by using root-mean-square errors. Finally, we find that the Lasso regression model is the optimal regression model, which can pick the key factors affecting the financial income of Zhejiang province for the four balances: tourism earned foreign exchange earnings, the average wage of urban employees employed, the ratio of the third industry to the second industry, and the RMB deposits of all financial institutions.
Keywords:Government Receipts, Best Subset Selection, Forward Stepwise Selection, Backward Stepwise Selection, Ridge Regression, Lasso Regression
基于数据挖掘技术的浙江省财政收入影响因素分析
庄亮亮,吴统
温州大学数学与信息科学学院,浙江 温州
收稿日期:2017年9月30日;录用日期:2017年10月19日;发布日期:2017年10月27日

摘 要
财政是政府实现其职能的基础,承担着资源整合、资源再分配以及宏观经济调控的职能。与此同时,财政也是社会经济发展水平的重要体现。由此可见,提高财政收入的预测精度对国家、地方来说意义重大。为了提升浙江省财政收入的预测精度,我们以R语言为编程工具,首先通过最优子集法、向前逐步回归法、向后逐步回归法、岭回归及Lasso法分别对浙江省财政收入的影响因素进行分析,得到了5种回归模型并通过它们各自的均方根误差(RMSE)来评估其回归效果。最后,选取Lasso回归模型为最优回归模型。其中,影响浙江省财政收入的关键性因素为:旅游创汇收入、城镇单位就业人员平均工资、第三产业与第二产业产值比、全部金融机构人民币存款余额这四项指标。
关键词 :财政收入,最优子集,向前逐步回归,向后逐步回归,岭回归,Lasso回归

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
1.1. 背景与意义
浙江省财政收入是浙江省经济指标体系中的核心指标之一,能综合反映浙江省的经济活动总量、评价其工业经济发展整体水平。随着社会主义市场经济体制的初步建成,浙江省财政收入的分析与预测等问题越来越被省内各级领导所重视。科学、合理地预测浙江省财政收入,对于克服年度预算收支规模的随意性和盲目性、正确处理浙江省财政收入与经济的相互关系具有十分重要的指导意义。
下面先来看看十二五期间浙江省财政局官方公布的浙江省财政收支情况:2010~2014年,浙江省财政收入分别为2608.47亿、3150.80亿、3441.23亿、3796.92亿和4122.02亿元,年均增长12.0%。2010~2014年,全省财政支出分别为3207.88亿、3842.59亿、4161.88亿、4730.47亿和5159.57亿元,年均增长13.0%。从这组数据可以看出这一期间浙江省财政收入与支出存在不平衡现象。众所周知,从2015年1月1日起我国开始施行的新《预算法》强调各级政府必须建立跨年度预算平衡机制。对财政收入与支出进行合理预测一直是政府在财政管理实践中需要解决的问题,准确的预测可以有效提高政府预算编制质量和财政管理效率。对浙江省政府而言,及时对我省的财政收入进行合理有效的预测,不仅可以有力贯彻“依法治税”的精神,还可以有效帮助我省解决预决算偏离度过大的问题。
1.2. 我国学者、专家对于财政收入的研究及观点
财政收入的来源比较复杂,因此它的影响因素也是多方面的,不同的专家、学者选择不同的影响因素研究财政收入,得到的结论也不同。杨欢 [1] 使用最小二乘法对财政收入进行多元回归分析,发现商品房销售额和消费品零售额对财政收入有较高的影响程度。刘荣 [2] 使用逐步回归法对我国财政收入进行影响因素的定量分析,他发现建筑业与工业对财政收入有较大的影响。周忠辉 [3] 等人对我国1998年~2009年财政收入进行实证研究分析,通过E-view排除模型的多重共线性进行回归分析,得到税收与GDP对财政收入影响程度较高的结论。金欣雪 [4] 等人使用最小二乘法建立了财政收入影响因素的多元线性回归模型。刘睿智、杜溦 [5] 等通过普通最小二乘法与Lasso方法模型的对比发现,普通最小二乘法不能解决变量间的共线性问题,而使用最优子集变量选择法以及Lasso方法可以较好地解决这类问题。徐菁 [6] 主要通过协整分析对建立的多元回归模型进行修正,从而得到最佳的回归模型。
结合以上各位学者专家的研究,本文采用最优子集法、向后逐步回归法等方法进行选取最优模型,得到了各自的回归模型并通过检验R2的大小,对比均方误差MSE和均方误差根RMSE来评估各自的回归效果。最后得出相对较优的模型进行财政收入预测。
1.3. 分析方法与过程
在本次研究浙江省财政收入的影响因素以及财政收入的预测中,影响因素的选取是构造预测模型的关键。因此,选择科学、合理、尽可能全面的影响因素是研究的重要前提。本研究根据浙江省统计年鉴中的现有信息,把就业、社会投资、生产总值、消费水平等各个方面因素纳入研究范围。本文通过最优子集选择法、向后逐步回归法以及其他选取最优变量的模型,发现使用Lasso方法选取的效果优于其他方法。
1.4. R语言函数及相关知识介绍
summary()函数:可以计算得到最小值、最大值、四分位数和数值型变量的均值,以及因子向量和逻辑型向量的频数统计。
regsubsets()函数:可以通过穷举搜索、正向或向后逐步或顺序替换来选择模型。本文主要利用此函数进行向前逐步回归和向后逐步回归来选取模型。
相关系数:是用来衡量两个数据集合是否在一条线上面,它用来衡量定距变量间的线性关系。相关系数的绝对值越大,相关性越强:相关系数越接近于1或−1,相关度越强;相关系数越接近于0,相关度越弱。
方差膨胀因子(Variance Inflation Factor, VIF):是指解释变量之间存在多重共线性时的方差与不存在多重共线性时的方差之比。 越大,显示共线性越严重。经验判断方法表明:当0 < VIF < 10,不存在多重共线性;当10 < VIF < 100,存在较强的多重共线性;当VIF ≥ 100,存在严重多重共线性。
BIC (Bayesian Information Criterions,贝叶斯信息规则):是对模型的拟合效果进行评价的一个指标,BIC值越小,则模型对数据的拟合越好。
AIC (Akaike information criterion,最小信息准则):可以表示为: ,它建立在熵的概念基础上,可以权衡所估计模型的复杂度和此模型拟合数据的优良性。AIC值越小,则模型对数据的拟合越好。
2. 变量指标选择
2.1. 数据选择
通过查阅文献资料以及了解财政收入及各个类别收入的来源等,本文所选用的16个指标如下表1所示(1985年~2015年)。
2.2. 数据预处理和探索性分析
我们发现所找到的各类数据均未出现缺失值。
下面我们使用R语言中函数summary( )计算出了各个指标的最小值、最大值、平均值和标准差。见表2 。
Table 1. Various factors index categories
表1. 各个因素指标类别表
*所有数据来自浙江省统计信息网——统计年鉴。
Table 2. Descriptive statistics of each index
表2. 各个指标的描述性统计量
从表2我们可知旅游创汇收入(x3)、城镇单位就业人员平均工资(x4)、人均生产总值(x11)的均值很大,而第三产业与第二产业产值比(x10)均值特别的小。
下列使用变量Pearson相关系数矩阵来描述各个变量之间的关系,见表3:
Table 3. Pearson correlation coefficient matrix
表3. Pearson相关系数矩阵表
由表3可以看出各个因素与财政收入y有较高的正相关关系。
与此同时通过对各个因素进行方差膨胀因子的检验,来验证因素之间的多重共线性。
由表4方差膨胀因子检验可知,除了x2、x10其他各因素的方差膨胀因子均大于100,存在严重多重共线性。
3. 模型建立
3.1. 最优子集回归模型
回归的方程的选择就是依据某种选择变量的准则,从对因变量y有影响的自变量集合中选择最优的子集,它与y构成如下回归方程:
衡量最优子集的常用标准主要有:
1) BIC或AIC达到最小;
2) Cp统计量达到最小;
3) 复判决定系数达到最大。
以下使用R语言中ISLR包和leaps包来进行影响财政收入(y)的最优子集的选择。
首先采用交叉验证法来选择最优模型的个数,由此方法所得的最优子集的个数为5个,并且调整后的R2为0.9998。
对整个数据集使用R语言中函数regsubsets( )来进行最优子集选择,以获得该5变量模型的参数估计结果,具体见表5。
结论:因此运用该方法选择的最优子集为(x1,x8,x9,x11,x16)。得到的回归模型为
我们得出测试均方误差MSE为36,345.680,RMSE为190.645。
3.2. 向前逐步选择回归模型
y先用全部1个变量建立回归方程,然后再从模型中增加变量。之后对重要的变量重新建立回归模型,并对此模型进行系数的显著性检验,以此类推,逐步增加模型的变量。
通过利用R语言程序regsubsets( )函数可得本次向前逐步回归法选择BIC最小的模型(BIC最小值为−214.5707,变量是为11个)作为最优模型,如图1所示。并且各影响因素在回归模型中的系数如表6所示。
Table 4. Variance inflation factor test
表4. 方差膨胀因子检验
Table 5. Optimal subset parameter estimation table
表5. 最优子集参数估计表
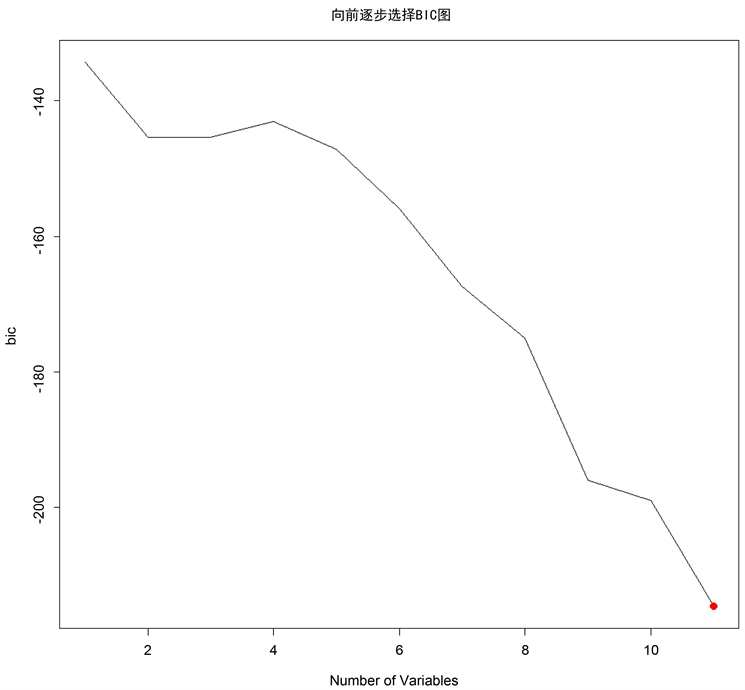
Figure 1. The results of BIC forward stepwise regression model generated
图1. BIC对向前逐步选择回归模型产生的结果
Table 6. Forward stepwise regression model coefficients
表6. 向前逐步回归模型系数表
并且调整后的R2为0.9997。运用向前逐步选择方法得到的回归模型为:
我们得出测试均方误差MSE为154,046.770,RMSE为232.480。
3.3. 向后逐步选择回归模型
先用全部m个变量建立回归方程,然后再从模型中剔除不重要的变量。之后对剩下的变量重新建立回归模型,并对此模型进行系数的显著性检验,以此类推,逐步减少模型的变量。
通过利用R语言程序regsubsets( )函数可得本次向后逐步回归法选择BIC最小的模型(BIC值为−221.90878,变量是为12个)作为最优模型,如图2所示。并且各影响因素在回归模型中的系数如表7所示。
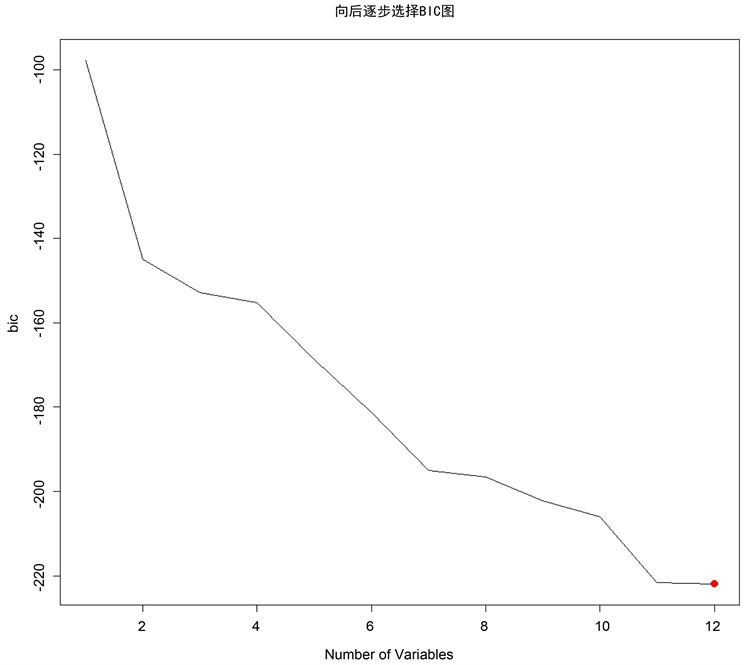
Figure 2. The results of BIC on backward stepwise choice regression model
图2. BIC对向后逐步选择回归模型产生的结果
Table 7. Backward Stepwise regression model coefficients
表7. 向后逐步回归模型系数表
并且调整后的R2为0.9997,运用向后逐步选择方法得到的回归模型为:
我们得出测试均方误差MSE为169,698.56,RMSE为264.005。
3.4. 岭回归模型
假定自变量数据矩阵 为 的,通常最小二乘法回归寻求那些使得残差平方和最小的系数 ,即
岭回归则需要一个惩罚项来约束系数的大小,其惩罚项就是上面的公式中增加一项 ,即岭回归的系数既要使得残差平方和小,又不能使得系数太膨胀:
使用交叉验证选择最优的lambda值为245.85。用训练集数据在最优lambda条件下建立岭回归模型,此模型的系数如下表8。
运用岭回归方法得到的回归模型为:
我们得出测试均方误差MSE为18,227.41,RMSE为135.009。
3.5. Lasso回归模型
Lasso方法的参数估计定义如下:
在上式中 ,是惩罚项。
首先使用交叉验证选择最优的lambda值,得到的最优的lambda值为45.008,相应的测试误差MSE为12,951.780,RMSE为113.806。
通过Lasso方法所得到的模型系数如表9所示。
Table 8. Model coefficients of ridge regression
表8. 岭回归模型系数表
Table 9. Coefficients of Lasso model
表9. Lasso模型系数表
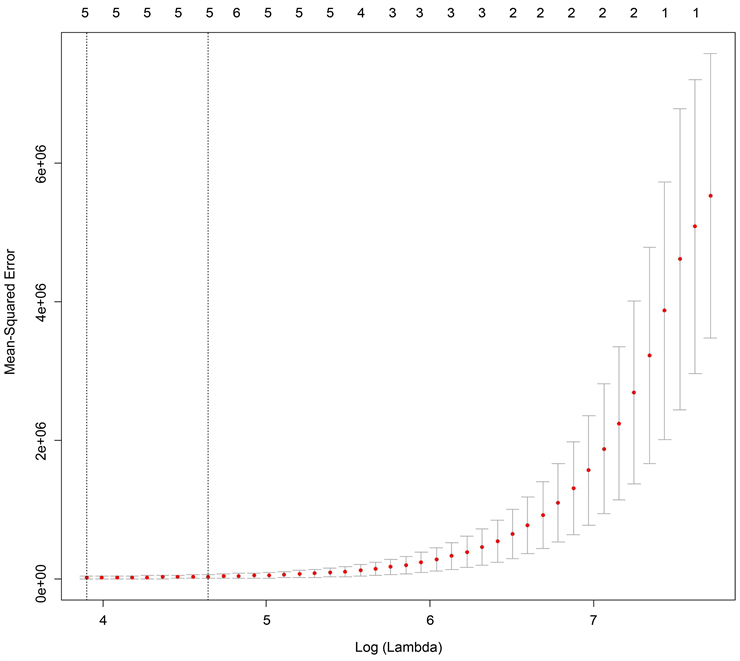
Figure 3. Mean-Squared error of lambda
图3. Lambda的均方误差
运用Lasso回归方法得到的回归模型为:
通过上述图3可以得知 的均方误差在4-5之间较好,所以我们可以选择出四变量模型,分别与旅游创汇收入、城镇单位就业人员平均工资、第三产业与第二产业产值比、全部金融机构人民币存款余额这四项指标有关。
4. 各模型比较
由下表10我们可以得知,向前逐步回归、向后逐步回归和最优子集回归所得到模型的均方误差和均
Table 10. Descriptive statistics of each index
表10. 各个指标的描述性统计量
方根误差较大,岭回归模型所得到的均方误差较小主要是因为通过放弃最小二乘法的无偏性,以损失部分信息、降低精度为代价获得回归系数。所以综上所述我们可以通过使用Lasso方法选取变量,其所得到的均方误差最小为12,951.780,最优变量为四变量,分别与旅游创汇收入、城镇单位就业人员平均工资、第三产业与第二产业产值比、全部金融机构人民币存款余额这四项指标有关。
5. 总结
本文通过对最优子集法、验证集方法、岭回归法、Lasso回归法等进行比较,发现使用Lasso回归方法选取变量的效果最优。于是对浙江省的财政收入以及各个类别收入的影响因素进行筛选时,我们采用的是Lasso回归方法。
由Lasso选择变量方法可知影响财政收入的关键因素主要与旅游业、城市人口、产业占比、金融存款与贷款有密切关系。其次从表格中可以看出通过Lasso选取变量时x10 (第三产业与第二产业产值比)所占比重最大。因此要实现浙江省的财政收入的增长不仅需要加快旅游业的发展,与此同时,合理制定银行存贷款利率,控制好城市人口总数,促进个人以及企业存贷款的积极性也是必由之径。最重要的是提高第三产业与第二产业产值比,加快服务业的发展,加速科技创新。
致谢
在本次论文设计过程中,黄辉林老师对该论文从选题、构思到最后定稿的各个环节给予细心指引与教导,使我们得以最终完成论文设计。另外还要感谢众多老师的关心支持和帮助。在此,谨向老师们致以衷心的感谢和崇高的敬意!本项目得到了温州市科技局软科学项目(项目名称:基于数据挖掘技术的温州市财政收入的建模分析与预测(No. R20160005))和温州大学大学生创新创业项目(NO. DC2016040)的大力支持,特此表示感谢。
文章引用
庄亮亮,吴 统. 基于数据挖掘技术的浙江省财政收入影响因素分析
Analysis of Influencing Factors of Fiscal Revenue in Zhejiang Province Based on Data Mining Technology[J]. 数据挖掘, 2017, 07(04): 93-104. http://dx.doi.org/10.12677/HJDM.2017.74011
参考文献 (References)
- 1. 杨欢. 地方财政收入影响因素的实证分析[J]. 时代金融, 2012(3): 156.
- 2. 刘荣. 基于逐步回归方法的国家财政收入的影响因素分析[J]. 劳动保障世界(理论版)公共科学, 2012(5): 51-54.
- 3. 周忠辉, 丁建勋, 王丽丽. 我国财政收入影响因素的实证研究[J]. 宏观经济, 2011(8): 84-85.
- 4. 金欣雪, 周红林. 我国财政收入影响因素分析[J]. 科技情报开发与经济(经济问题探讨), 2007, 17(26): 140-142.
- 5. 刘睿智, 杜溦. 基于LASSO变量选择方法的投资组合及实证分析[J]. 经济问题, 2012(9): 103-107.
- 6. 徐菁. 财政收入与经济增长关系研究——以杭州市为例[D]: [硕士学位论文]. 杭州: 浙江大学, 2008.
